06. 특성 공학과 규제

colab link

feature engineering and regularization

1. 다중 회귀
여러 개의 특성을 사용한 선형 회귀 를 다중회귀 라 부른다. 특성이 많은 고차원에서는 선형회귀가 매우 복잡한 모델을 표현할 수 있다.

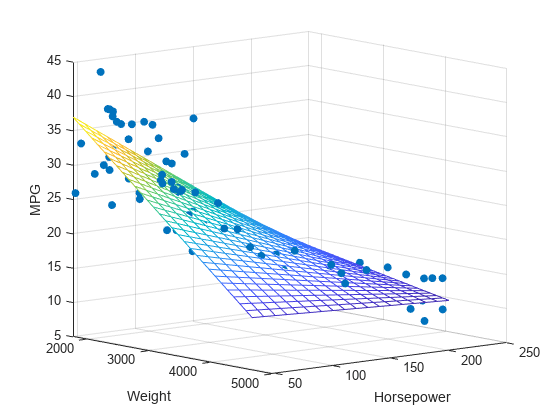
각 특성을 서로 곱해서 또다른 특성을 만들 수 있다. 이렇게 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업을 특성 공학이라 한다.

2. 데이터 준비

판다스는 데이터 분석라이브러리로 데이터프레임은 판다스의 핵심 구조이다. (CSV 확장 파일을 사용, 엑셀과 유사한 형태)

1) 판다스의 read_csv() 함수에 주소를 넣어 파일을 가져온다
2) to_numpy() 메서들를 사용해 넘파이 배열로 바꾼다.

df = pd.read_csv('https://bit.ly/perch_csv_data')
perch_full = df.to_numpy()
print(perch_full)

3. 사이킷런의 변환기
특성을 만들거나 전처리하기 위해 사이킷런에서 제공하는 다양한 클래스를 변환기라 한다.

• Polynomial Features 클래스

훈련을 해야 변환이 가능하므로 fit 한 후 transform을 수행한다.
fit()메서드는 새롭게 만들 특성 조합을 찾고 transform() 메서드는 실제로 데이터를 변환

poly = PolynomialFeatures()
poly.fit([[2,3]])
print(poly.transform([[2,3]])) # polynomial features 미리 예시

poly = PolynomialFeatures(include_bias = False) #1 제외하기
poly.fit(train_input)
train_poly = poly.transform(train_input) #다중 특성 고려된 train_input 배열
print(train_poly.shape) #9개의 열 -> 9개의 특성으로 증가

9개의 특성이 어떻게 만들어졌는지 확인하기 위해서get_feature_names_out() 메서드를 호출해 각기 어떤 입력의 조합으로 만들어졌는지 확인한다.

poly.get_feature_names_out() #어떻게 특성 생성했는지 확인

# result
# array(['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2','x2^2'], dtype=object)

test_poly = poly.transform(test_input) #테스트 세트도 다중 특성 적용

4. 다중 회귀 모델 훈련하기

다중 회귀 모델을 훈련하는 것은 선형 회귀 모델을 훈련하는 것과 같다. 여러 개의 특성을 사용해 선형회귀를 수행하는 것

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly, train_target) #다중 특성 고려된 poly_train 배열로 훈련하기
print(lr.score(train_poly, train_target))

poly = PolynomialFeatures(degree = 5, include_bias = False) #고차항 ~5차항까지
poly.fit(train_input) #고차항의 특성 고려한 모델로 훈련
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(train_poly.shape) #특성이 55개로 증가

훈련 특성을 증가할 수록 훈련세트에 과대적합 됨을 유의한다.

5. 규제

규제는 머신러닝 모델이 훈련세트를 너무 과도하게 학습하지 못하도록 훼방하는 것. 선형회귀모델의 경우 특성에 곱해지는 계수의 크기를 작게 만드는 것을 예시로 들 수 있다.

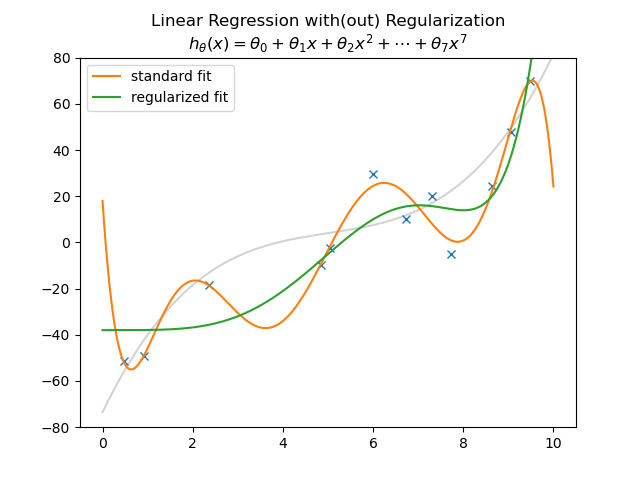
기울기가 작아질 경우 일반화된 모델을 도출할 수 있다.

단, 스케일이 정규화되지 않을 경우 공정하게 제어되지 않으므로 반드시 정규화를 한 후 규제해야 한다. (선형 회귀 모델의 계수를 다 동등하게 규제하기 위해 정규화 한다. 한 특성의 영향력만 과하지 않도록)

#다중 회귀 모델에서 과대적합없이 다중 특성을 사용하기 위해 규제
#즉, 특성 줄일 필요 없고 여러개의 특성 사용가능하도록 함
from sklearn.preprocessing import StandardScaler
ss= StandardScaler() #규제를 위해 우선 선형모델의 각 계수를 정규화하기
ss.fit(train_poly)
train_scaled = ss.transform(train_poly) #각 훈련세트의 스케일 맞추기
test_scaled = ss.transform(test_poly) #훈련세트의 스케일이 아닌, 각 테스트 세트의 스케일 맞추기

1) 릿지 회귀 (L2 model)
규제하는 방법으로 릿지 회귀, 라쏘 회귀 2가지가 존재.

릿지는 계수를 제곱한 값을 기준으로 규제를 적용하고 라쏘는 계수의 절댓값을 기준으로 규제를 적용한다.

릿지와 라쏘 모델에서 alpha 매개변수로 규제의 강도를 조절한다. alpha 값이 크면 규제강도가 세지므로 계수 값을 더 줄이고 조금 더 과소 적합되도록 유도한다.

• 전체적인 과정

1) train/test set를 준비한다
2) 정규화해 scale를 조절한다.
3) 규제 + 선형회귀 => 릿지 모델

# 정규화 했으니 이제 규제하기
# 선형모델을 규제하는 데에는 릿지모델, 라쏘 모델 2가지 존재
# 각 모델은 선형회귀모델 + 규제 기능 추가된 것
# 즉 릿지, 라쏘 모델에 선형회귀모델 훈련 기능도 포함돼 있음

from sklearn.linear_model import Ridge #선형회귀모델에 릿지 포함돼 있음
ridge = Ridge()
ridge.fit(train_scaled, train_target) #정규화 된 훈련세트로 릿지모델 훈련하기
print(ridge.score(train_scaled, train_target))

적절한 alpha 값을 찾는 한가지 방법은 alpha 값에 대한 R^2 값의 그래프를 그리는 것이다. 훈련세트와 테스트 세트의 점수가 가장 가까운 지점이 최적의 alpha 값이 된다.

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100] #적합한 규제변수 alpha 찾기
for alpha in alpha_list:
  #릿지 모델을 만듭니다
  ridge = Ridge(alpha=alpha)
  #릿지 모델을 훈련합니다
  ridge.fit(train_scaled, train_target)
  #훈련점수와 테스트 점수를 저장합니다
  train_score.append(ridge.score(train_scaled, train_target))
  test_score.append(ridge.score(test_scaled, test_target))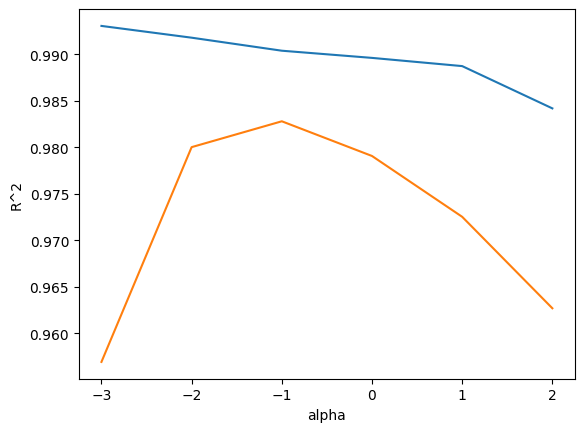

왼쪽을 보면 훈련세트에는 잘 맞고 테스트 세트에는 맞지 않는 과대적합, 오른쪽 편은 훈련세트와 테스트 세트의 점수가 모두 낮아지는 과소적합의 모습을 보인다.

2) 라쏘 회귀 (L1 model)

|가중치|로 규제한다.
Ridge 클래스를 Lasso 클래스로 바꾼다.

from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target))

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100] #적합한 규제변수 alpha 찾기
for alpha in alpha_list:
  #라쏘 모델을 만듭니다
  lasso = Lasso(alpha=alpha, max_iter = 10000) #max_iter는 뭘까?
  #라쏘 모델을 훈련합니다
  lasso.fit(train_scaled, train_target)
  #훈련점수와 테스트 점수를 저장합니다
  train_score.append(lasso.score(train_scaled, train_target))
  test_score.append(lasso.score(test_scaled, test_target))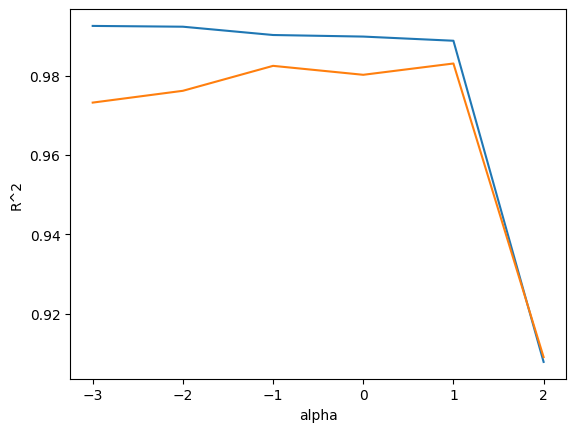

라쏘 모델은 계수값을 아예 0으로 설정가능하다. 계수가 0일 경우 특성이 의미 없어지고 즉, 특성을 사용하지 않음을 의미한다.

print(np.sum(lasso.coef_ == 0)) #라쏘 모델에서 무시한 특성들 개수 출력

일반적으로 라쏘보단 릿지모델(L2)가 적합하다.