문제
자연수 x를 y로 변환하려고 합니다. 사용할 수 있는 연산은 다음과 같습니다.
x에 n을 더합니다
x에 2를 곱합니다.
x에 3을 곱합니다.
자연수 x, y, n이 매개변수로 주어질 때, x를 y로 변환하기 위해 필요한 최소 연산 횟수를 return하도록 solution 함수를 완성해주세요. 이때 x를 y로 만들 수 없다면 -1을 return 해주세요.
해결방법
내가 푼 방식으로는 테스트케이스를 다 통과하지 못했다.
그래서 다른 풀이방법 찾아봤음.
디버깅 이해 필요함.
풀이 방법을 찾아보니 DP가 시간 효율성은 더 좋았고,
BFS로도 문제를 해결할 순 있었다.
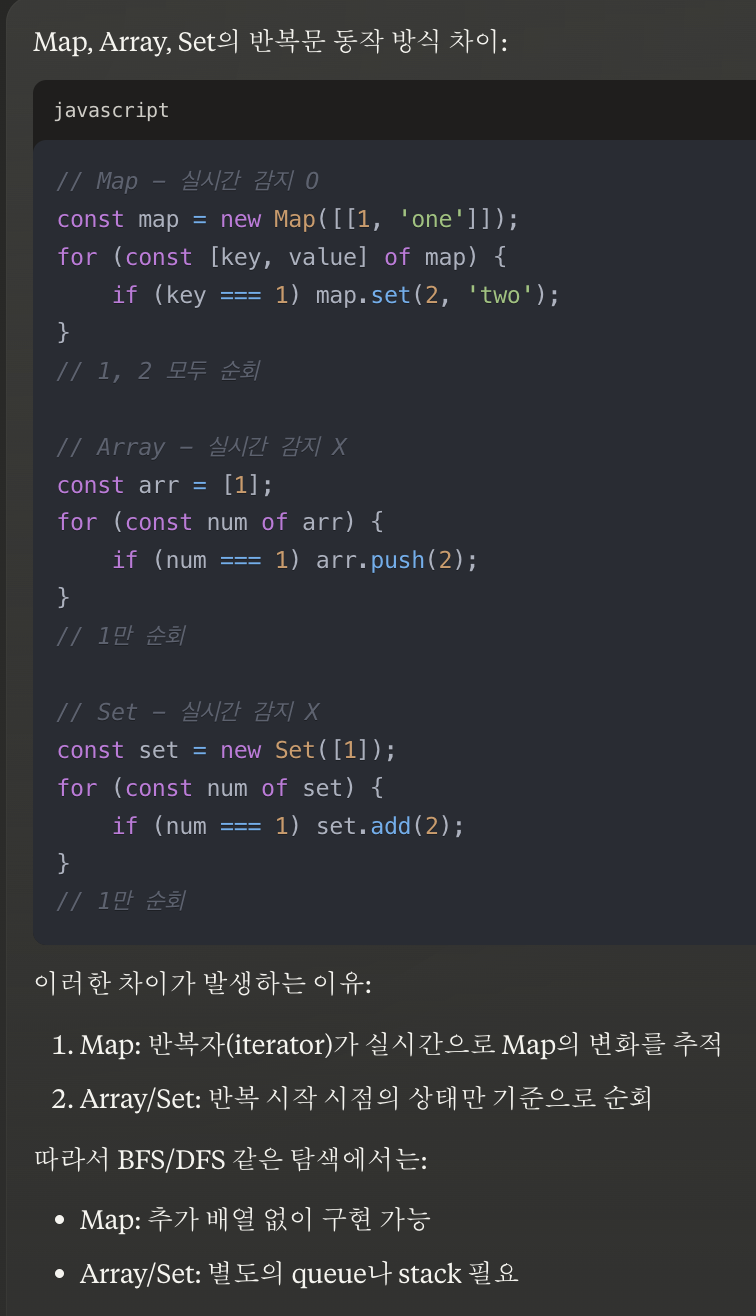
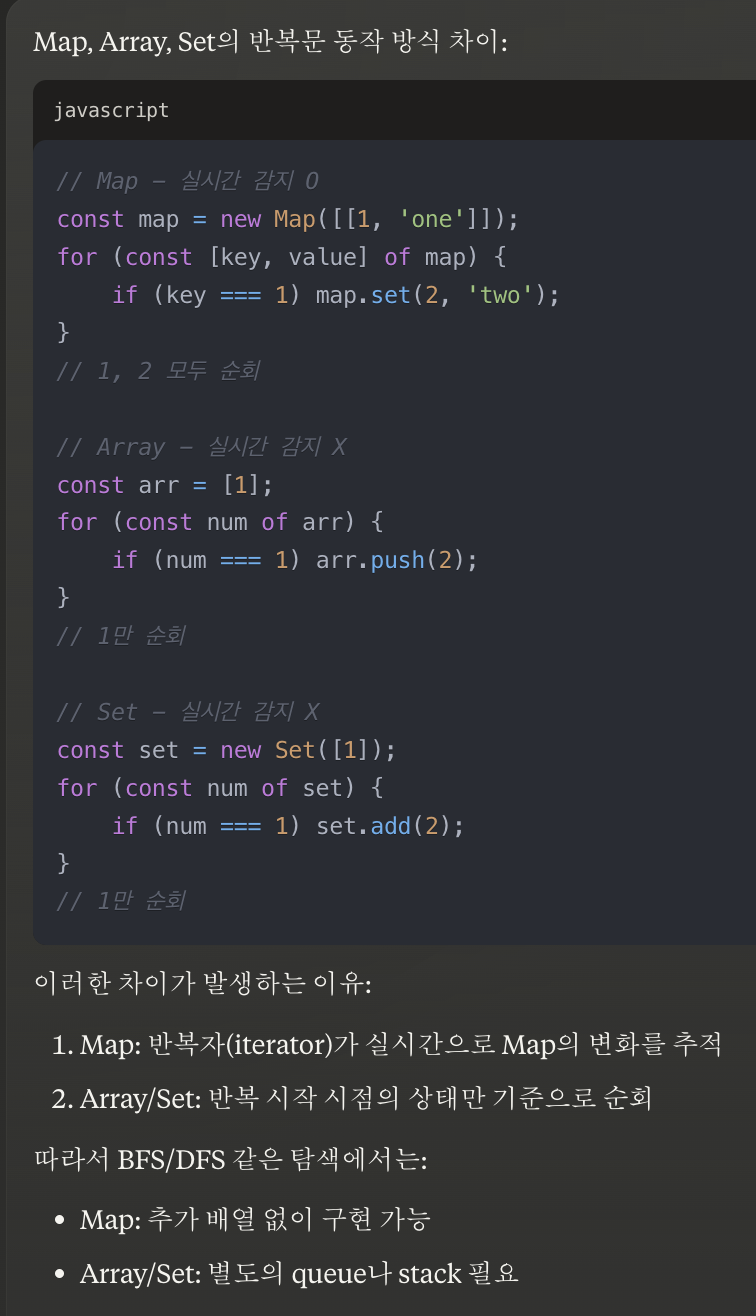
풀이 2: BFS + Map은 추가된 요소 반복문 추가로 돌수 있다
초기 인덱스 값 0으로 설정하고, 배열 arr에 Map key값 추가해줘서
현재 반복문이 아닌 while문에서 조건 검사 다시해서 돌고,
인덱스값을 통해 shift 역할을 할 수 있다.
하지만 Map은 그 자체로 [current, count] 으로 꺼낼 수 있기 때문에
굳이 index, array를 이용할 필요가 없었다. !
최적화된 코드로 기억해두자.
그리고 반복문 돌 때, 처음에 존재하지 않은 key값일 때 count값 기록해두고, 다음 차례일 때 cnt+1된 값으로 다시 key값에 count값 기록된다.
function solution(x, y, n) {
if (x === y) return 0;
const queue = new Map([[x, 0]]); // key: 숫자, value: 연산 횟수
for ( let [cur,cnt] of queue){
for (const next of [cur + n, cur * 2, cur * 3]) {
if (next === y) return cnt + 1;
if (next > y || queue.has(next)) continue;
queue.set(next, cnt + 1);
}
}
return -1;
}풀이 1: BFS 풀이
set으로 문제풀이하면 시간초과가 떠서 map으로 풀어야 한다.
function solution(x, y, n) {
if (x === y) return 0;
const queue = new Map([[x, 0]]); // key: 숫자, value: 연산 횟수
let index = 0;
const arr = [x]; // queue 역할
while (index < arr.length) {
const cur = arr[index++];
const cnt = queue.get(cur);
for (const next of [cur + n, cur * 2, cur * 3]) {
if (next === y) return cnt + 1;
if (next > y || queue.has(next)) continue;
queue.set(next, cnt + 1);
arr.push(next);
}
}
return -1;
}풀이 2: DP 풀이
DP 배열의 의미
dp[i]: 숫자 x에서 i를 만들기 위한 최소 연산 횟수
배열을 Infinity로 초기화하는 것은 아직 도달하지 못한 숫자를 표시하기 위함
dp[x] = 0: 시작 숫자는 연산이 필요 없으므로 0으로 초기화
function solution(x, y, n) {
const dp = new Array(y+1).fill(Infinity);
dp[x] = 0;
for(let i=x; i<y; i++){
dp[i+n] = Math.min(dp[i+n],dp[i]+1);
dp[i*2] = Math.min(dp[i*2],dp[i]+1);
dp[i*3] = Math.min(dp[i*3],dp[i]+1);
}
return dp[y]!==Infinity? dp[y] : -1;
}
BFS, DFS, DP의 차이점과 공통점
공통점 :
1. 모두 문제 해결을 위한 체계적인 접근 방법
2. 상태 공간을 탐색한다는 점
3. 방문 처리가 필요한 경우가 많음
차이점 :
1.탐색방식
1)BFS : 레벨단위 탐색
2)DFS : 경로단위 탐색
3)DP : 하위문제 단위 탐색
2.메모리 사용
1)BFS : 큐에 많은 상태 저장
2)DFS : 재귀스택 사용
3)DP : 결과값 테이블 사용
3.최적해 보장
1)BFS: 최단경로 보장
2)DFS: 최단경로 보장x
3)DP: 최적부분 구조일 때 최적해 보장
이 문제의 경우 BFS나 DP가 적합한 이유:
1. 최소 연산 횟수를 찾아야 함.
2. 상태가 숫자 하나로 단순함
3. 중복 계산을 피해야 함.
BFS(너비 우선 탐색)
- 특징: 같은 레벨의 모든 노드를 먼저 탐색
- 구현: Queue 사용
- 장점: 최단 경로 보장
- shift 연산 사용 시, 시간 복잡도 => O(n)
맨 앞에 있는 값을 제거한 후에 기존 배열에 있던 모든 원소를 한 자리씩 왼쪽으로 이동시켜야 하기 때문에 시간 복잡도가 O(n)이다.
-> shift 연산을 배열과 인덱스를 사용한 큐로 구현 가능하다. O(1)
// BFS 예시
const queue = [[start, 0]];
while(queue.length) {
const [current, count] = queue.shift();
// 인접한 모든 노드를 큐에 추가
}DFS(깊이 우선 탐색)
- 특징: 한 경로를 끝까지 탐색한 후 다음 경로 탐색
- 구현: Stack 또는 재귀 사용
- 장점: 메모리 사용이 적음
function dfs(current, count){
if(종료조건) return;
// 다음 노드로 재귀 호출
dfs(next, count+1);
}DP(동적 계획법)
- 특징: 문제를 작은 하위문제로 나누어 해결
- 구현: Map이나 배열에 결과 저장
- 장점: 중복계산 방지
// DP 예시 (앞서 본 코드)
const dp = new Array(y+1).fill(Infinity);
dp[x]=0;
for(let i=x; i<y; i++) {
dp[i+n]= Math.min(dp[i+n],dp[i]+1);
}