D+50 정수삼각형

문제

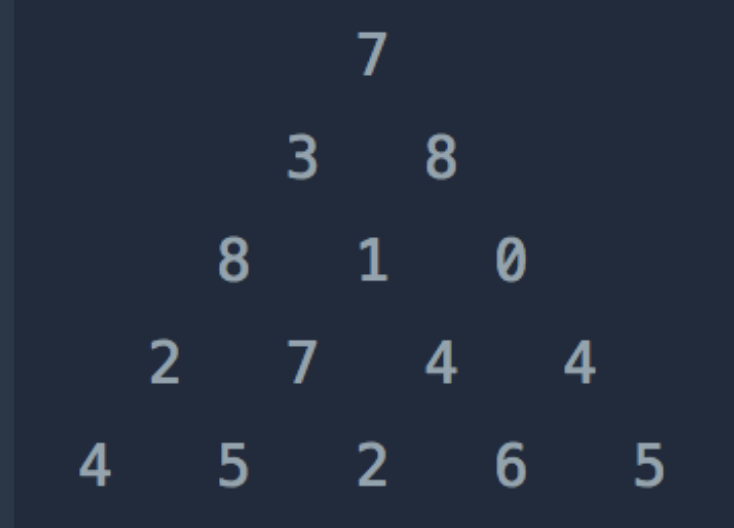
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

제한사항
삼각형의 높이는 1 이상 500 이하입니다.
삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
입출력 예
triangle result
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] 30

풀이

i=0 인덱스부터 시작할 때, dp[현재행][열] 접근가능한 열은 현재 인덱스와 [i][i+1] 접근가능.

1. Bottom-Up

테스트케이스 1개에서 시간초과 발생..!

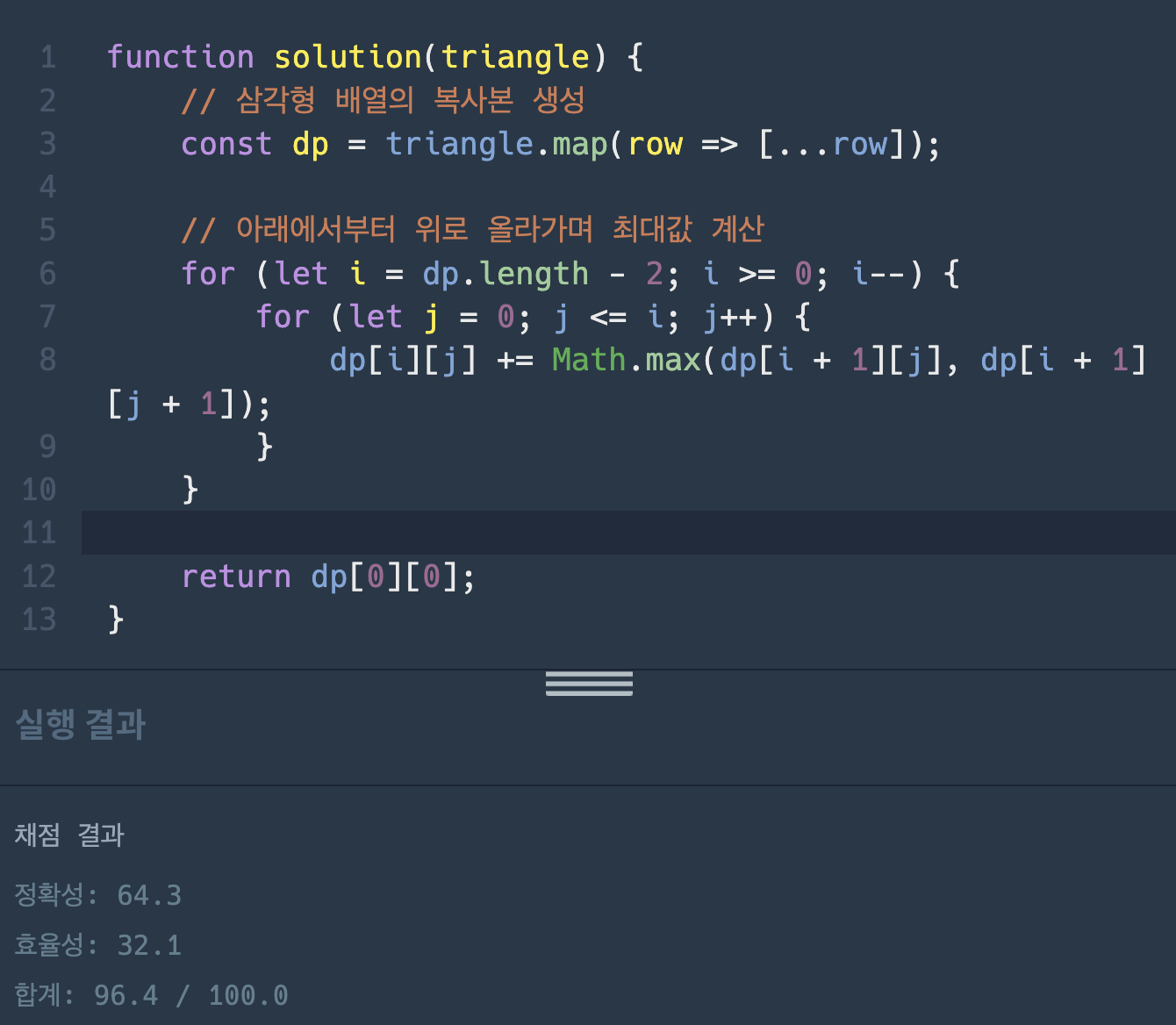
이유는 ...
시간복잡도: O(n²)
추가 공간복잡도: O(n²)
배열 복사에 따른 추가 오버헤드 발생
모든 위치를 순회해야 함

2.Top-Down (메모이제이션 방식)

function solution(triangle) {
    const memo = Array.from({ length: triangle.length }, 
        (_, i) => new Array(i + 1).fill(-1));
    
    function dfs(row, col) {
        if (row === triangle.length - 1) return triangle[row][col];
        if (memo[row][col] !== -1) return memo[row][col];
        
        memo[row][col] = triangle[row][col] + 
            Math.max(dfs(row + 1, col), dfs(row + 1, col + 1));
        return memo[row][col];
    }
    
    return dfs(0, 0);
}

성능 개선 핵심 포인트

메모리 접근 패턴:
연속된 메모리 접근이 캐시 효율성 향상
불필요한 메모리 할당 제거

데이터 구조 선택:
1차원 배열 사용으로 메모리 효율성 향상
불필요한 차원 제거

연산 최적화:
중복 연산 제거
불필요한 복사 연산 제거
결론적으로, Top-Down 방식이 더 빠른 이유는:

필요한 경로만 계산
메모이제이션으로 중복 계산 즉시 방지
재귀 호출의 오버헤드가 배열 복사 오버헤드보다 작음