Hyperparameter Optimization
왜 필요할까?
- 모델 성능 향상
- 과적합 및 과소적합 방지
- 학습 효율성 개선
- 복잡한 검색 공간 탐색
- 자동화된 머신러닝
- 재현성 및 신뢰성
Manual Search
하이퍼파라미터 값들을 결정할 때, 논문에서 사용한 데이터셋과 내가 사용하고자 하는 데이터셋이 다르기 때문에, 완벽하게 적용되기 어렵다. 일반적으로 직관이나 노하우에 의해 다음 하이퍼파라미터 값을 선정하고, 학습을 수행하고, 검증 데이터셋에 대해 측정한 성능 결과를 기록한다. 마지막 시점까지 시도한 다음 가장 높은 성능을 발휘한 하이퍼파라미터 값들을 선정한다.
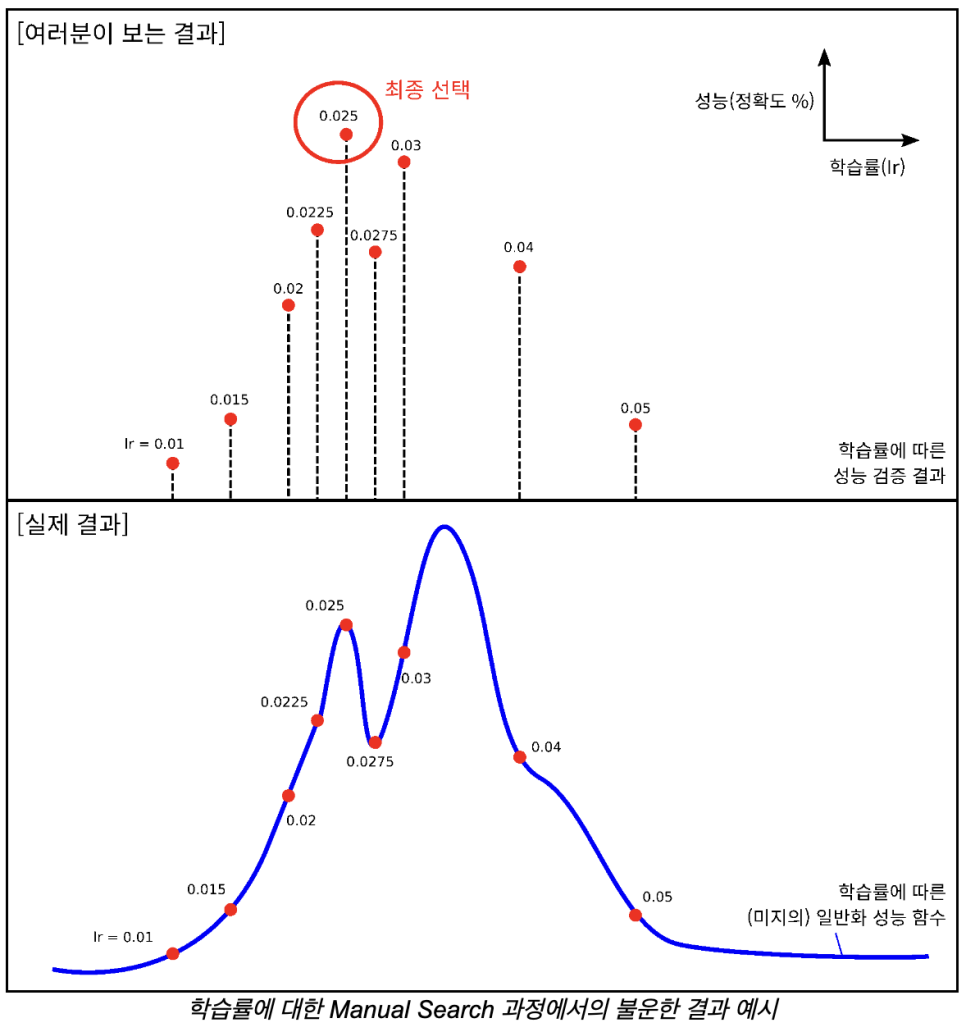
직관적인 방법이지만, 운에 좌우된다는 점이 단점.
추가적으로, 한 번에 여러 종류의 하이퍼파라미터를 탐색할 때 문제가 복잡해진다. 여러 종류의 하이퍼파라미터들이 서로 간의 상호 영향 관계를 나타내는 경우, 기존의 직관을 적용하기 어렵다. 대표적인 예시가 학습률-L2 정규화 항.
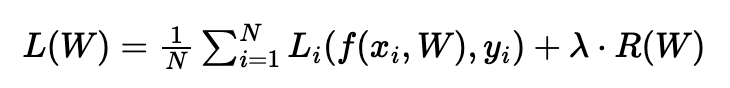
L2 정규화 계수인 ℷ를 변화시키면, 손실함수의 형태가 변화한다. 이로 인해 최적 학습률의 값도 자연스럽게 변화한다.
Grid Search, Random Search
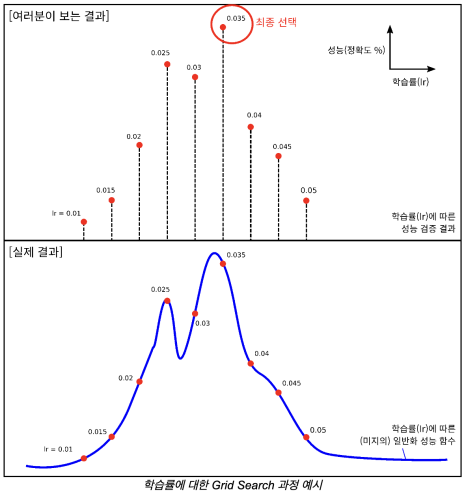
상대적으로 체계적인 방식. Grid Search는 탐색 대상이 되는 특정 구간 내의 후보 하이퍼파라미터 값들을 일정 간격으로 선정하여 결과 비교. 더 균등하고 전역적인 탐색이 가능하다.
Random Search도 큰 맥락은 유사하지만, 탐색 구간 내 후보 하이퍼파라미터 값들을 랜덤 샘플링으로 선정. 불필요한 반복 수행 횟수를 줄이고, 정해진 간격 사이에 위치한 값에 대해서도 확률적 탐색 가능. 그러나 여전히 불필요한 탐색 반복. 다음 시도할 후보에 이전 성능 결과에 대한 '사전지식'이 반영되지 않기 때문.
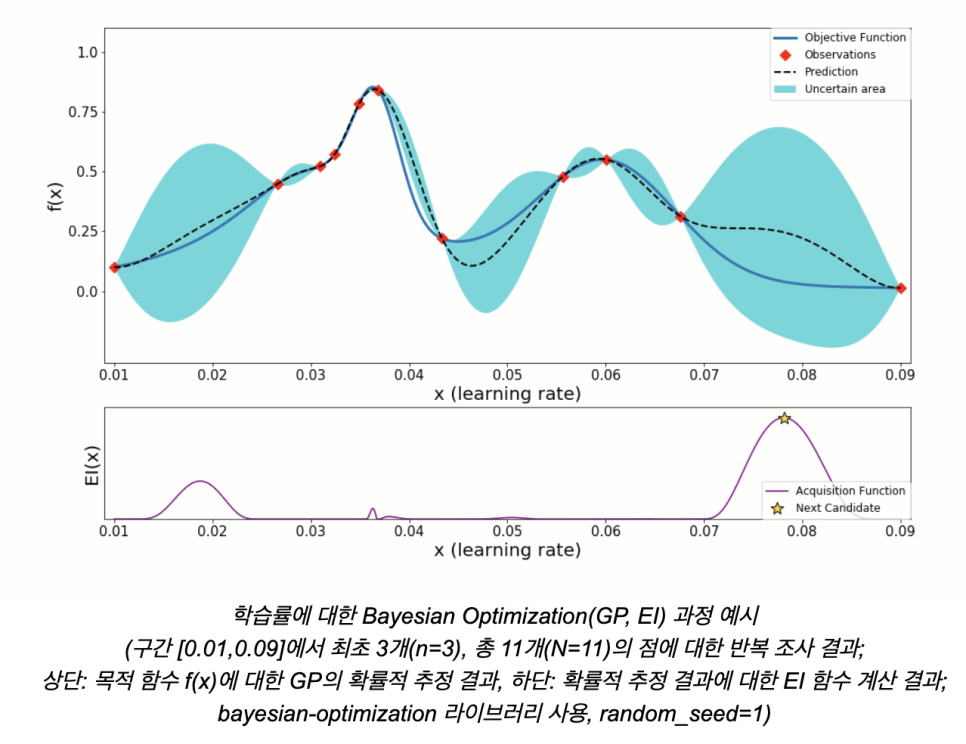
Bayesian Optimization
Bayesian Optimization(BO)은 원래 미지의 목적함수 f를 상정하고 f(x)를 최대로 만드는 최적해 x를 찾는 것을 목적으로 한다. 목적함수의 표현식을 명시적으로 알지 못하고, 하나의 함숫값을 계산하는데 오래 걸릴 경우 가정. 가능한 적은 수의 후보들에 대해 함숫값을 순차적으로 조사하여 f(x)를 최대로 만드는 최적해를 효과적으로 찾는 것이 주요 목표이다.
BO의 두 가지 필수 요소
- Surrogate Model : 현재까지 조사된 입력값-함숫값 점들 (x_1, f(x_1)), ...(x_t, f(x_t))를 바탕으로 목적함수의 형태에 대한 확률적인 추정을 수행하는 모델
- Acquisition Function : 목적함수에 대한 현재까지의 확률적 추정 결과를 바탕으로 최적 입력값 x를 찾는 데 있어 유용할만한 다음 입력값 후보 x_t+1을 추천해주는 함수

Surrogate Model로 가장 많이 사용되는 확률 모델이 Gaussian Process(GP)이다. 함수들에 대한 확률 분포를 나타내기 위한 확률 모델, 구성 요소 간의 결합 분포가 가우시안 분포를 따름.
핵심은 조사된 점으로부터 거리가 먼 x일수록, 해당 지점에 대해 추정한 평균값의 불확실성이 크다.
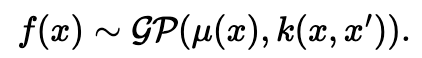
Acquisition Function은 선정되는 x_t+1이 최적 입력값을 선정하는데 유용해야 한다. 이 유용하다는 것이 지금까지 조사된 점들 중 함숫값이 최대인 점 근방을 시도하는 것이 합리적이다 이런 뜻. 이 경우가 exploitation. 혹은, 조사된 두 점 사이에 위치하고, 표준편차(=불확실성)가 큰 경우, 탐색해봐야 한다는 것이 어느정도 그럴싸한 판단이다.이것이 exploration.
Expected Improvement(EI)는 exploration과 exploitation 두 전략 모두 일정 수준 포함하도록 설계된 것으로, Acquisition Function으로 가장 많이 사용된다. 현재까지 추정된 목적함수를 바탕으로 최대 합숫값보다 큰 함숫값을 도출할 확률 및 그 함숫값과의 차이값을 종합적으로 고려하여 입력값 x의 유용성을 나타내는 숫자를 출력한다.
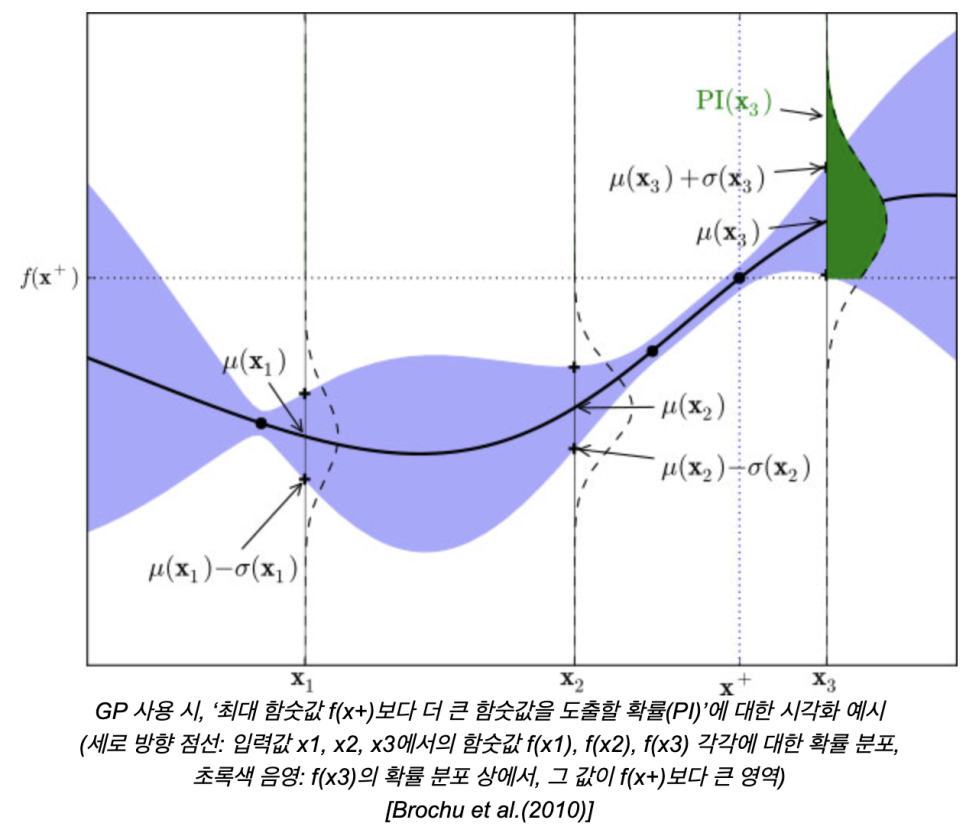
최대 함숫값보다 큰 영역에 해당하는 부분이 초록색으로 표시되어 있음. 이 영역의 크기가 클 수록, 이 때의 함숫값이 지금까지의 최댓값보다 클 확률이 높다. 그런 x값은 유용할만한 후보로 판단할 수 있다. 이렇게 계산한 PI값에 함숫값에 대한 평균과 지금까지의 최댓값과의 차이값만큼 가중하여 EI값을 최종적으로 계산. 그런 가능성이 존재할 때, 그 값이 실제로 얼마나 더 큰가 또한 고려대상이기 때문에 이를 반영한 계산 방식.
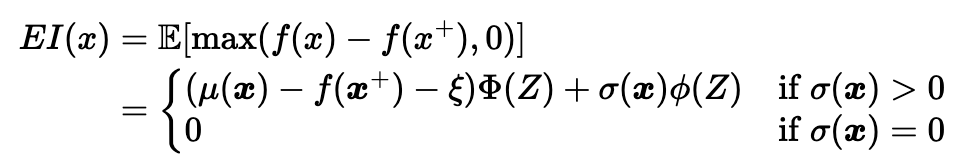
긴 유도과정을 거치면 이렇게 정리된다.Φ와 ϕ는 각각 표준정규분포의 누적분포함수(CDF)와 확률분포함수(PDF)를 나타내며, ℇ는 exploration과 exploitation 간의 상대적 강도를 조절해 주는 파라미터이다. 이걸 크게 잡을수록 exploration의 강도가, 작게 잡을수록 exploitation의 강도가 높아진다.
실제 딥러닝 모델에서의 수행 예시
- 입력값 x : 학습률
- 목적함수 f(x) : 설정한 학습률을 적용하여 학습한 딥러닝 모델의 검증 데이터셋에 대한 성능 결과 수치 (정확도 등)
- 입력값 x의 탐색 대상 구간 : (a, b)
- 맨 처음에 조사할 입력값-함숫값 점들의 갯수 : n
- 맨 마지막 차례까지 조사할 입력값-함숫값 점들의 최대 개수 : N
- 초기 샘플링: 구간 (a, b)에서 n개의 입력값을 랜덤하게 샘플링하여 딥러닝 모델을 학습하고, 검증 데이터셋으로 성능을 평가하여 함숫값 계산.
- Surrogate Model: 초기 샘플들을 이용해 Surrogate Model로 확률적 추정 수행.
- 입력값 선택: 탐색된 점이 총 N개에 도달할 때까지, Surrogate Model의 추정 결과를 바탕으로 EI 값을 계산하여, 값이 가장 큰 점을 다음 입력값 후보로 선택.
- 모델 학습: 선택된 입력값을 사용하여 딥러닝 모델을 학습하고 성능을 평가하여 함숫값으로 간주.
- 반복: 새로운 점을 기존 점들에 추가하고 Surrogate Model을 갱신. 이 과정을 N개의 점이 모일 때까지 반복.
- 최종 최적해 선택: 최종적으로 추정된 목적함수 결과물 중 평균 함수 µ(x) 를 최대로 만드는 최적해를 선택.