P(model)과 P(data I model)을 통해 P(model I data) 추정
함수의 특정 x값에 대한 y값만 알 수 있고, 함수의 수학적 표현을 모를 때, 함수의 최댓값을 계산하기 위한 방법으로 사용.
소량의 실험 값과 확률적 추정으로 미지의 목적함수에 대한 최적값을 효과적으로 탐색할 수 있는 방법.
초기 추정치를 업데이트하면서 최적값을 찾아가는 방식. 실제 시스템에서 매개변수 조정이나 하이퍼파라미터 튜닝에 많이 사용.
베이지안 최적화 활용
- 하이퍼파라미터 최적화 :
머신러닝 모델에서 사용되는 하이퍼파라미터 조정, 최적의 하이퍼파라미터 값을 찾을 수 있음. 예를 들어, SVM(Support Vector Machine), 신경망, 랜덤 포레스트 등의 모델에서 매개변수인 커널의 유형, 커널 함수의 매개변수, 학습률, 은닉층 수 등 조정, 딥러닝 모델에서의 하이퍼파라미터 조정. - 실험 최적화 :
베이지안 최적화의 기본적 사용에서 확장, 실험 디자인에서 베이지안 최적화 사용. 실험 재현성을 높이기 위해 실험 환경 조정, 실험에서 얻은 데이터를 최대한 활용하기 위해 실험의 파라미터 조정 등. 일반적으로 가장 좋은 성능을 뽑는 조건을 찾아내어 적용하기 위해 활용.
베이지안 최적화 과정
- 사전 분포 설정(Prior Distribution) :
함수의 초기 추정치 설정. 주로 가우시안 프로세스(Gaussian Process, GP)사용, 함수의 예측 분포 모델링 - 획득 함수(Acquisition Function) :
함수의 다음 평가 지점 선택. 주어진 사전 분포를 바탕으로 다음 샘플링 위치 결정. 주로 기대 개선(Expected Improvement), 확률 개선(Probability of Improvement), 상한 신뢰 구간(Upper Confidence Bound) 사용. - 함수 평가 :
선택된 지점에서 실제 함수 평가. 실제 데이터나 실험을 통해 결과 획득. - 사후 분포 업데이트 :
평가된 결과를 바탕으로 사전 분포 업데이트, 새로운 사후 분포 계산. 베이즈 정리를 통해 이루어짐. - 반복 :
위 단계 반복하여 최적화. 각 반복에서 새로운 정보를 얻어 이를 기반으로 더 정교한 최적화 수행.
Bayesian Optimization Algorithm
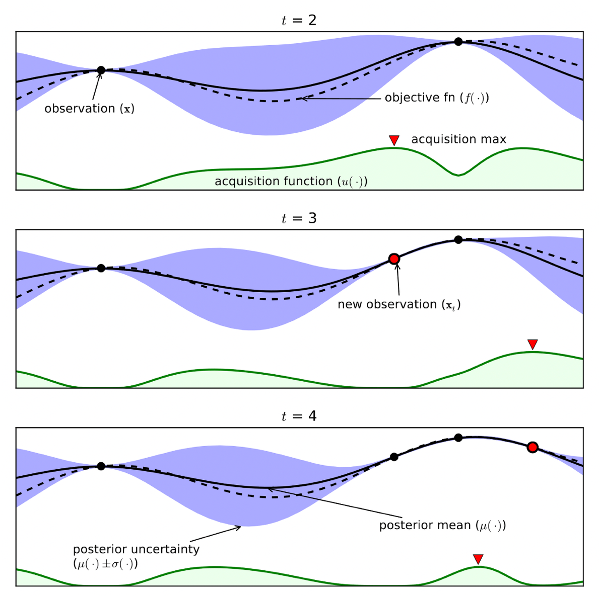
- 목적함수 f(x) : 우리가 구하고자 하는 함수 (검은 점선)
- Surrogate Model : 목적함수의 형태에 대한 확률적 추정 (검은 실선)
- 실제 측정 값 : 검은색 점
- Acquisition fuction : 다음 번 탐색할 입력 값 후보 추천 함수 (녹색 실선)
- 파란색 영역은 불확실성 정도
Progress
해당 모델에 데이터셋 입력. 데이터셋을 통해 딥러닝 모델 학습이 이루어지고 결과 계산 후 우리가 확률적으로 추정하는 Surrogate Model이 그려짐.
이미 가지고 있는 데이터셋 이후, 다음 iteration에서 측정할 하이퍼파라미터의 위치로서 Acquisition function 값이 큰 점을 후보로 선정.
Acquisition function은 모델을 통해 어떤 결과를 얻고 싶은가에 따라 다르다. 목적함수의 불확실성을 최소화하거나, 예측값을 최대/최소화할 수 있을 것으로 기대되는 포인트가 선정되도록 함수를 만든다. 전자가 탐색 전략 혹은 적극적 학습 전략, 후자가 활용 전략.
결과로서 나온 해당 샘플링 포인트에 대한 측정을 실시하고 그 측정값을 데이터에 편입. 그럼 모델은 추가된 데이터에 기반하여 목적함수의 추정 업데이트.