[그래픽스] 좌표계 변환 (= 공간 이전, space change)

YEOM JINSEOP·2023년 11월 19일

Computer Graphics

목록 보기

5/14

⭐ object space -----world transform-----> world space

⭐ world space -----view transform-----> camera space

⭐ camera space -----projection transform-----> clip space

⭐ clip space -----viewport transform-----> screen space

vertex shader가 수행하는 세 가지 transform

1️⃣ object space -- world transform --> world space

vertex array의 데이터 중, '위치'의 world transform

object space: 하나의 object를 모델링하는데 사용된 좌표계
world space: 각자의 object의 space에서 정의된 object들로 3D 가상 환경을 구성하기 위해서, 이들을 하나의 좌표계로 통합한 좌표계.
object space에서 각각의 object를 world transform(Scaling, Rotation, Translation)을 통해 world space로 옮겨진다.
world transform이 affine transform으로만 구성되었다면 $[L|t]$ 로 표기할 수 있다.
$L$ 은 '누적된 linear transform'을, $t$ 는 '누적된 translation'을 표현한다.

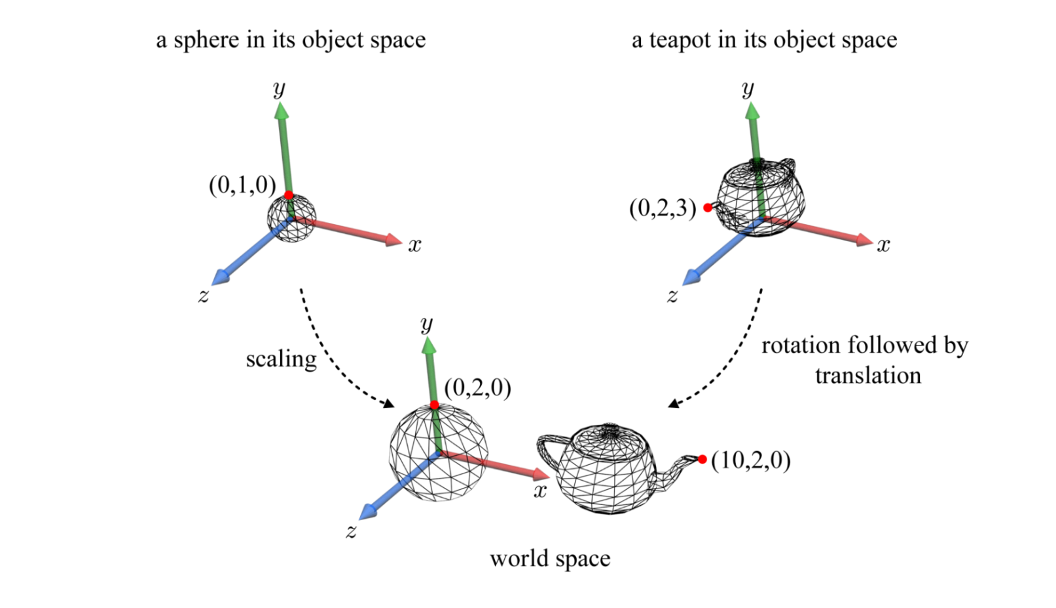
obejct space에서 한 object의 모델링이 완료되면, 그 object는 자신의 object space와 일체가 된다.
즉, object를 움직이게 되면 그 object space도 따라서 같이 움직인다.
물체에 적용되는 world transform에 따라서 object space의 기저도 달라지는 것이다.

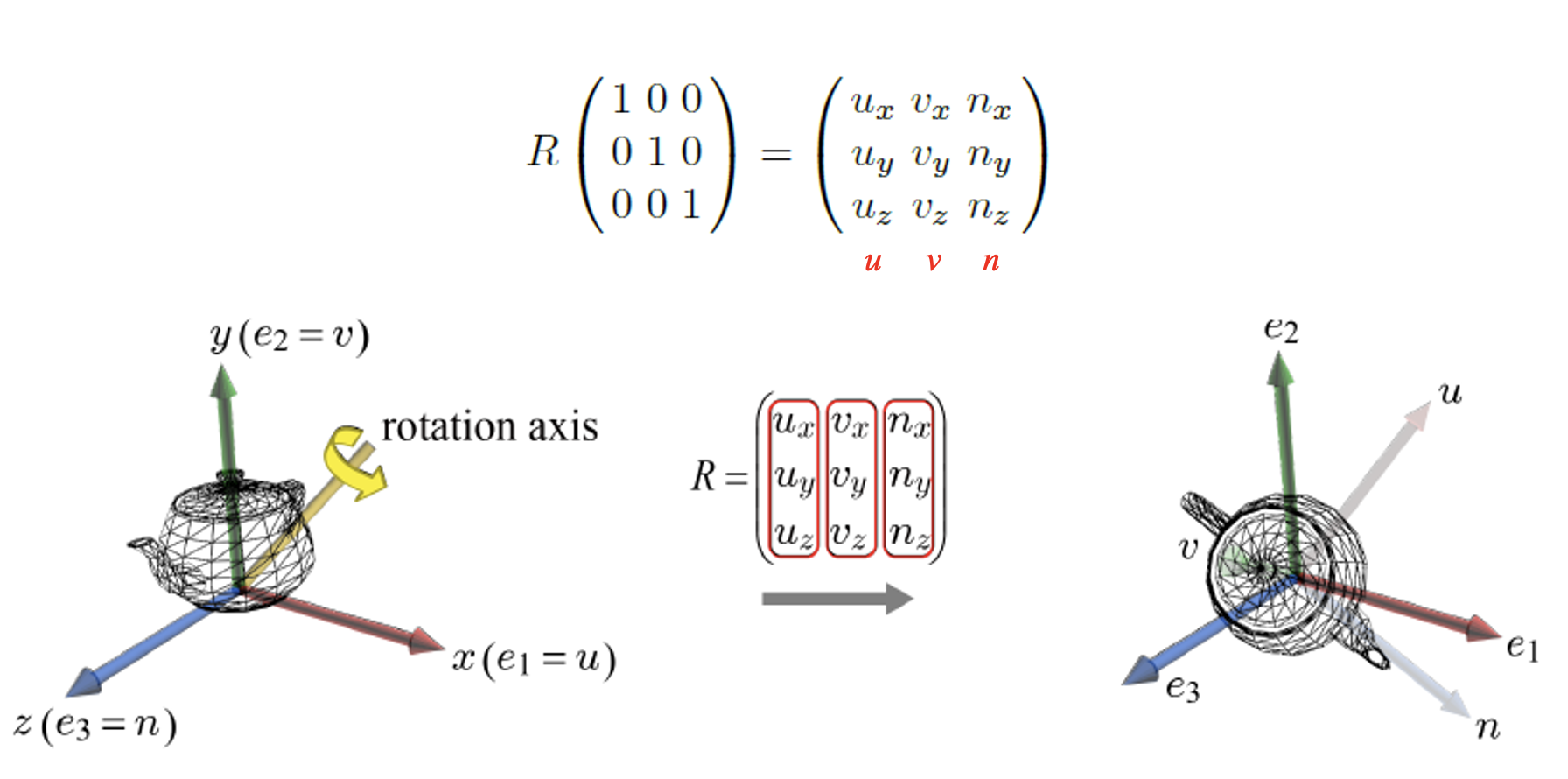
vertex array의 데이터 중, 'normal'의 world transform

vertex array의 중요한 데이터 중 또 하나인 'normal'에는 world transform을 바로 적용할 수 없다.
참고로, world transform이 affine transform으로만 구성되었다면 $[L|t]$ 로 표기할 수 있다.
이때, $L$ 은 '누적된 linear transform'을, $t$ 는 '누적된 translation'을 표현한다.
normal 변환에서 $t$ 는 무시해도 된다. 벡터는 translation에 의해 영향받지 않기 때문이다.
중요한 점은, normal의 world transform을 위해서는 $L$ 을 사용할 수는 없다.
normal의 world transform을 위해서는 $L$ 대신 $(L^{-1})^T$ 를 사용해야 한다.

2️⃣ world space -- view transform --> camera space

camera space

world transform이 완료되어 모든 object가 world space에 모아졌다고 가정하자.
world space의 특정 영역을 스크린에 rendering하기 위해서는, 가상 camera의 위치와 방향을 설정해야 한다.
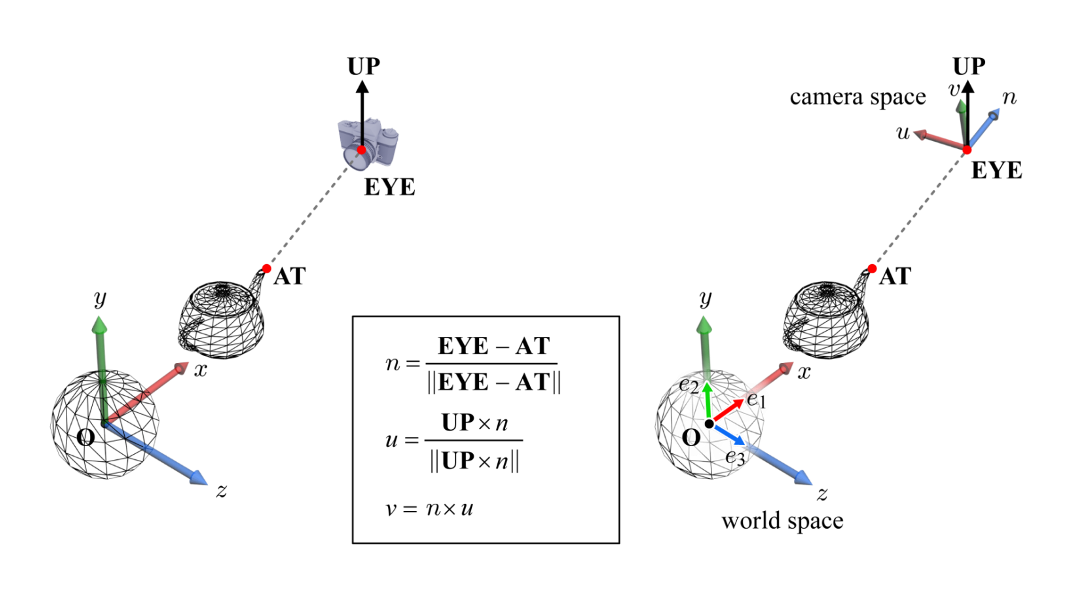
camera space: EYE, AT, UP parameter로부터 camera space가 정의된다.
camera space의 원점은 EYE이고, 기저는 $\{u,v,n\}$ 이다.
camera space를 $\{u,v,n, EYE \}$ 로 표기한다.
world space는 $\{e_1, e_2, e_3, O\}$ 로 표기한다. 여기에서 $O$ 는 원점을 의미한다.
EYE는 world space에서의 camera의 위치다.
AT은 world space에서 camera가 바라보는 기준점이다.
스크린에 담고자하는 object들이 모여 있는 space의 가운데 방향에 설정된다.
UP은 camera의 상단이 가리키는 방향을 대략적으로 묘사하는 벡터이다.
대부분의 경우, world space의 수직 방향 즉, $y$ 축으로 설정된다.
camera space의 기저 $\{u,v,n\}$
단위 벡터 $n$ : AT과 EYE를 잇는 벡터를 정규화
단위 벡터 $u$ : UP과 &n&의 벡터곱을 정규화
단위 벡터 $v$ : $n$ 과 $u$ 의 벡터곱

view transform ( = camera transform)

world space의 모든 vertex들이 camera space로 재정의되면, rendering 알고리즘을 설계 구현하는 것이 매우 쉬워진다.
world space의 모든 vertex들을 camera space로 재정의하려면,
EYE를 먼저 $O$ 로 translation 시킨 뒤, $\{u, v, n\}$ 을 $\{e_1, e_2, e_3\}$ 와 일치하도록 rotation 하면 된다.

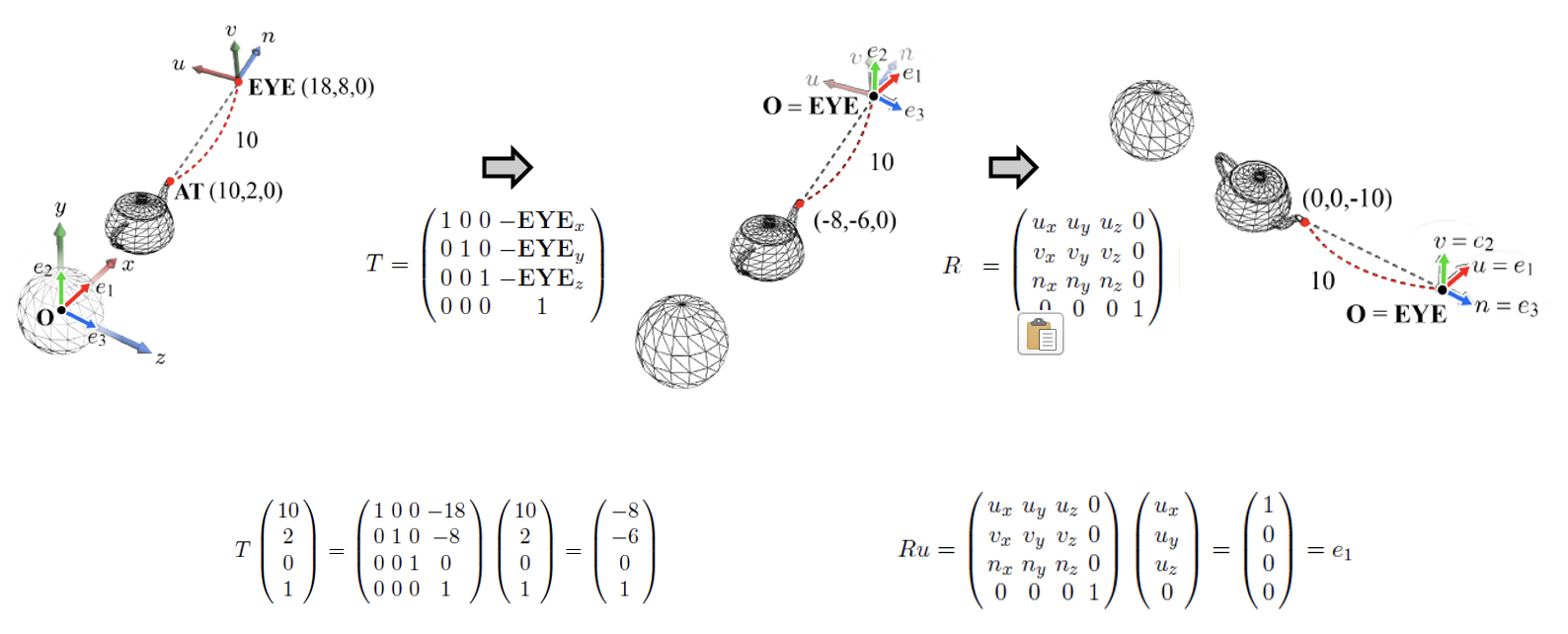
view transform을 $M_{view}$ 로 표기하는데, translation matrix $T$ 와 rotation matrix $R$ 을 결합한 4 $\times$ 4 matrix로 정의된다.

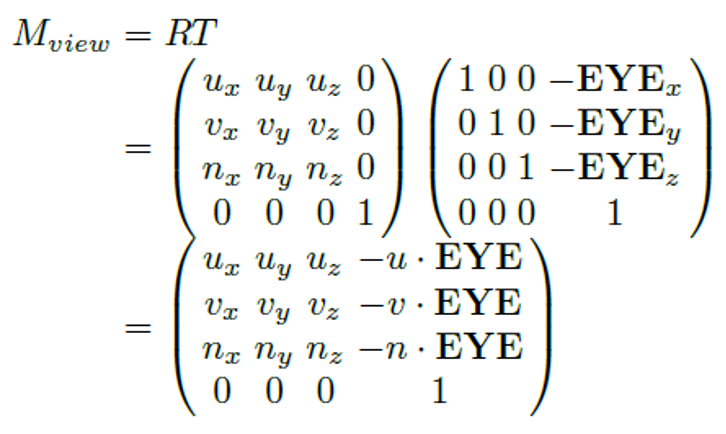
3️⃣ camera space -- projection transform --> clip space

world space에서 정의된 EYE, AT, UP을 camera의 'extrinsic' parameter라고 본다면,
카메라의 렌즈를 선택하고 줌인/줌아웃을 조절하는 것에 해당하는 'intrinsic' parameter를 정의할 것이다.
한편, view transform에 의해 world space의 모든 물체가 camera space $\{u, v, n, EYE\}$ 로 변환되었다면,
이제 더 이상 world space는 고려하지 않아도 되므로, $\{u, v, n\}$ 을 버리고 camera space의 축을 $x,y,z$ 로 표기할 것이다.

view frustum

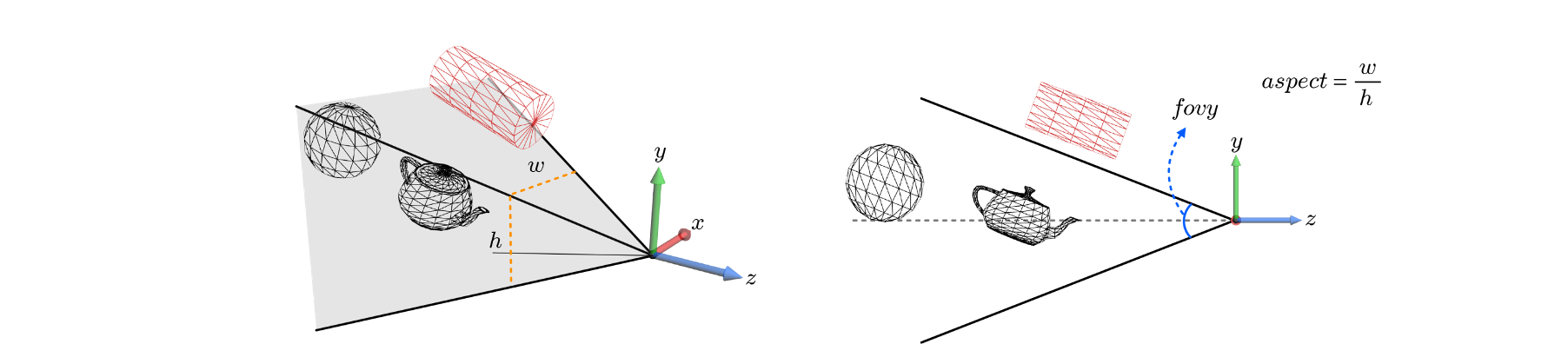
camera의 시야(field of view; fov)는 제한되어 있기 때문에,
camera space의 모든 object를 스크린에 담아낼 수 없다.
camera의 가시 영역을 view volume이라고 부르는데,
$fovy, aspect, n, f$ 네 가지 parameter를 사용해 결정된다.
$fovy$ : $y$ 축 기준의 시야각
$aspect$ : view volume의 가로세로 비율
➡️ $fovy$ 와 $aspect$ 에 의해 정의된 view volume은 꼭지점을 원점에 두고 $-z$ 축을 중심축으로 가진 무한한 크기의 피라미드가 된다
$n$ : 원점으로부터 near plane 까지의 거리
$f$ : 원점으로부터 far plane 까지의 거리
✅ near plane $z = -n$ 과 far plane $z = -f$ 에 의해 절단되어 유한한 크기의 view volume이 되는데, 이를 view frustum이라고 한다.
view frustum 바깥에 놓인 object는 보이지 않는 것으로 처리된다.
view frustum 바깥에 놓인 물체는 미리 걸러져서 GPU 파이프라인에 들어가지 못하게 한다.

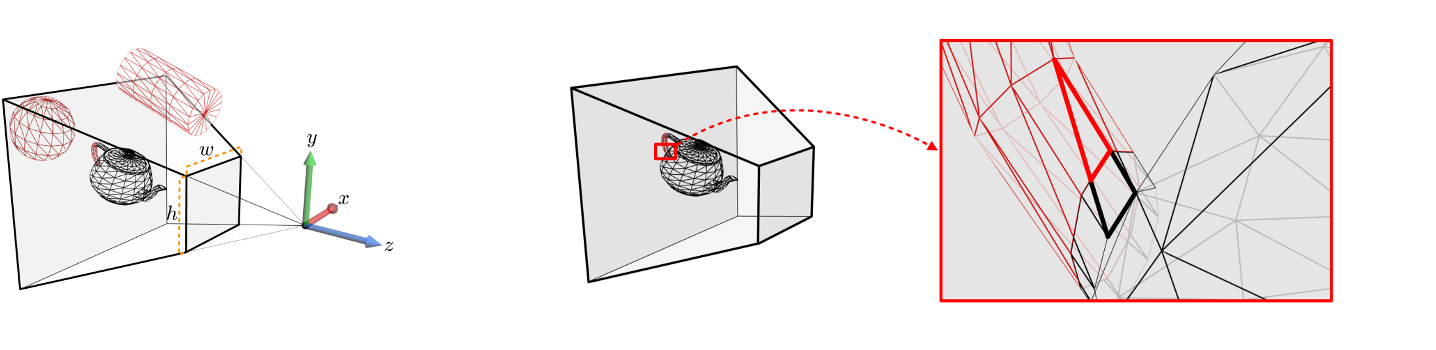
projection transform

하나의 polygon이 view frustum과 교차할 겨우,
polygon은 잘라져서 view frustum 안쪽에 놓인 부분만 GPU 파이프라인의 다음 단계로 넘어가게 된다.
이렇게 polygon을 자르는 작업을 cliping이라 부르는데, rasterizer에 의해 수행된다.
실제 cliping은 camera space에서 view frustum을 이용해 수행되지 않는다.
camera space의 object는 projection transform을 거친 뒤, 2 $\times$ 2 $\times$ 2 크기의 정육면체에 대해 cliping된다.
이때, 피라미드 모양의 view frustum을 좌표계의 주축에 나란한 2 $\times$ 2 $\times$ 2 크기의 정육면체 view volume으로 변형하는 것을 projection transform이라고 한다.
projection transform 이후 물체가 놓이는 공간을 clip space라고 따로 부른다.
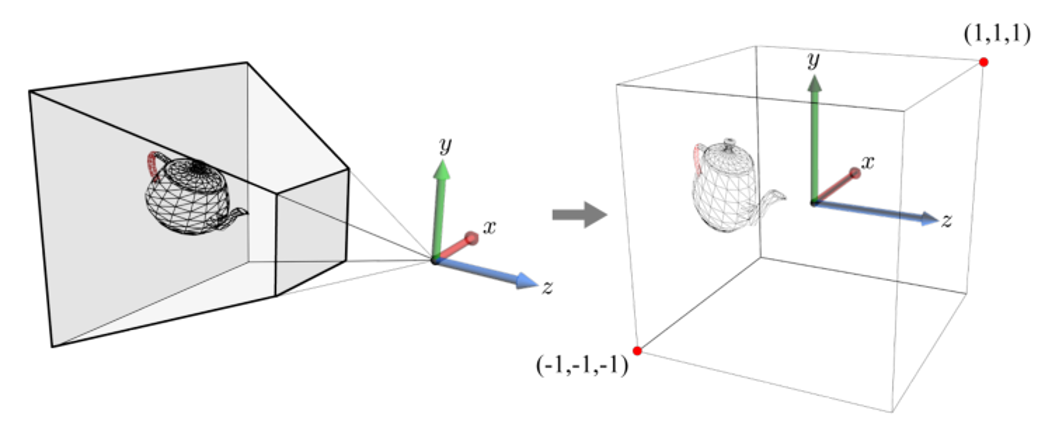
projection transform matrix $M$
$\\$
$M$ = $\begin{pmatrix} \frac{cot(\frac{fovy}{2})}{aspect} & 0 & 0 & 0 \\ 0 & cot(\frac{fovy}{2}) & 0 & 0 \\ 0 & 0 & \frac{f+n}{f-n} & \frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \end{pmatrix}$
clip space의 object는 rasterize로 입력되게 되는데,
clip space는 오른손 좌표계인 반면, rasterizer는 모든 object가 왼손 clip space에서 정의되어 있다는 가정에서 설계되어 있다.
따라서 오른손 좌표계를 왼손 좌표계로 변환해야 하는데, 이를 위해서는 정점 $z$ 좌표의 부호를 변경하면 된다.
$\\$
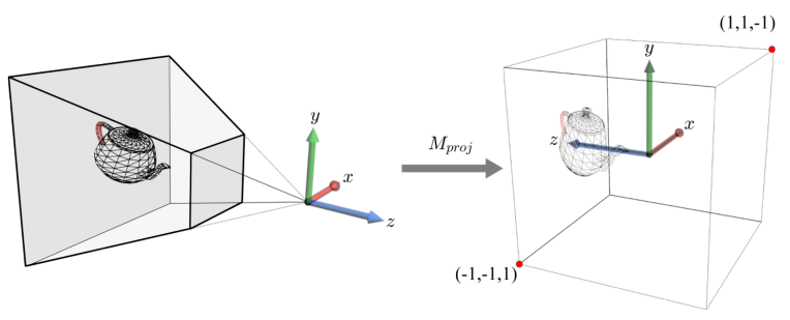
$M_{proj} =$ $\begin{pmatrix} \frac{cot(\frac{fovy}{2})}{aspect} & 0 & 0 & 0 \\ 0 & cot(\frac{fovy}{2}) & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \end{pmatrix}$

✅ projection transfrom은 3D 공간 내에서 원근법을 구현한다.

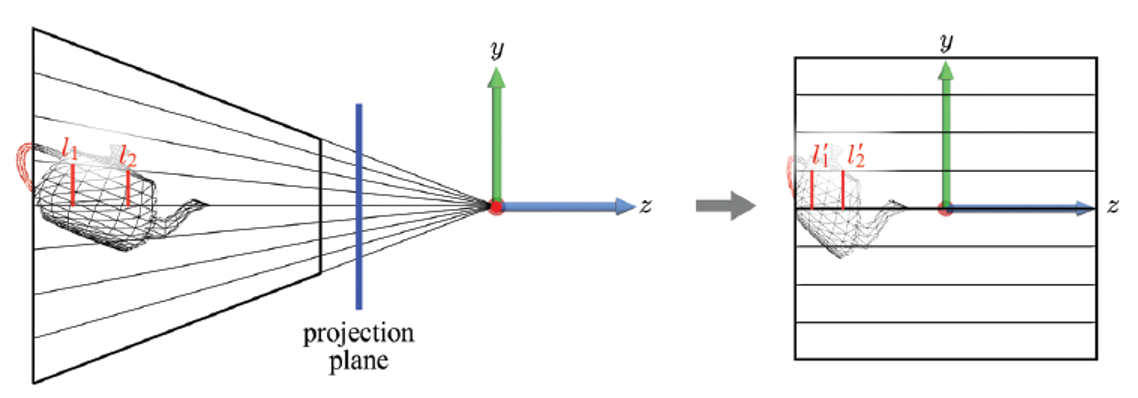
view frustum의 단면도를 보자.
view frustum은 원점에 위치한 camera로 수렴하는 projection line들의 집합으로 이해할 수 있다.
view frustum과 원점 사이에 놓여 있으면서, $z$ 축에 수직인 가상의 projection line을 생각해보면,
view frustum의 projection line은 projection plane에 영상을 형상할 것이다.
하나의 projection line 위에 존재하는 모든 3D 점은 projection plane의 한 점에 맺히게 된다.
두 선분 $l_1, l_2$ 를 보면, 3차원 공간에서는 $l_1$ 이 $l_2$ 보다 길지만, 이들은 projection plane에서 이들은 동일한 길이를 갖게 된다. 즉 멀리 있는 물체가 실제보다 더 작게 보이게 되는데, 이것이 바로 원근법이다.

4️⃣ clip space -- viewport transform --> screen space

컴퓨터 스크린 위의 윈도우는 그 자신의 좌표계를 가지는데,
이를 window space 혹은 screen space라고 부른다.
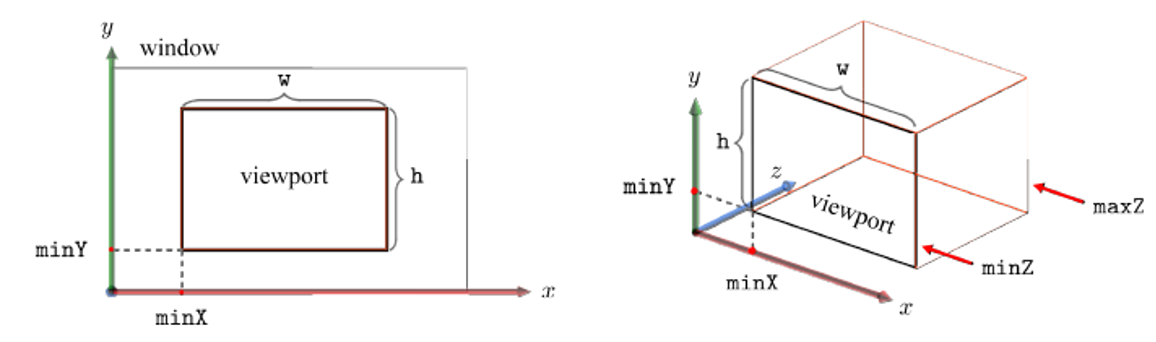
위 그림과 같이 window의 왼쪽 아래 모퉁이에 원점을 가진다.
한편, clip space 정육면체 view volume 안의 내용이 최종적으로 그려질 스크린 영역을 viewport라고 한다.
window에서 viewport의 범위는 glViewport에 의해 정의된다.
goViewport는 다음 parameter를 사용한다.
1) minX와 minY: viewport 왼쪽 아래 모퉁이의 screen space 좌표
2) w, h: viewport의 너비와 높이
viewport의 aspect ratio는 w/h가 되는데, 이는 view frustum의 parameter인 aspect와 동일하게 설정하는게 좋다.
clip space로 표현된 2 $\times$ 2 $\times$ 2 크기의 view volume은 viewport로 변환될 때,
scaling과 translation을 결합한 행렬에 의해 변환된다.
viewport transform =
$\\$
$\begin{pmatrix} \frac{w}{2} & 0 & 0 & minX + \frac{w}{2}\\ 0 & \frac{h}{2} & 0 & minY + \frac{h}{2}\\ 0 & 0 & \frac{maxZ-minZ}{2} & \frac{maxZ+minZ}{2} \\ 0 & 0 & 0 & 1 \end{pmatrix}$
viewport transform은 2 $\times$ 2 $\times$ 2 크기의 view volume 안에 있는 모든 vertex에 적용된다.