[핵심][20.04]AdaRound

AdaRound 논문
AdaRound 코드(출처: BRECQ)

---

기존

---

AdaRound

1. "optimize할 보조 변수 $\bold{V}$를 도입"

$where,$

• $\bold{V}_{i,j}$는 optimize할 continuous variable 이다.

  • $\bold{V}_{i,j}$를 도입하는 이유

    • a) continuous optimization problem
      원래의 문제는 이산적(discrete) 최적화 문제(가중치를 올림 또는 내림).
      $\bold{V}_{i,j}$를 도입함으로써 이를 연속적(continuous) 최적화 문제로 변환.

    • b) 미분 가능성
      $h(\bold{V}_{i,j})$는 미분 가능한 함수이므로(rectified sigmoid), gradient를 이용해 학습 가능.

    • c) 유연한 학습 및 점진적 이진화
      $\bold{V}_{i,j}$를 통해 각 가중치가 올림될지 내림될지를 부드럽게 학습 가능.
      regularization term $f_{reg}$와 함께 사용하여, $\bold{V}_{i,j}$가 0 또는 1에 가까운 값으로 점진적으로 수렴토록 함.

• $h(V_{i, j})$는 [0,1] 범위의 출력을 갖는 "미분 가능한 함수"이다.

  • AdaRound 논문에선 Rectified Sigmoid를 사용했다.
  • $h(V)$가 0에 가까우면 내림을, 1에 가까우면 올림을 하게 될 것이다.
  • $\zeta, \gamma$는 stretch parameter로 각각 1.1, -0.1로 고정.

• $f_{reg}(V)는$ $h(V_{i,j})$가 1 또는 0으로 수렴하게 하는 "미분 가능한 regularizer"이다.

  • 최적화 과정에서 h(V_{i,j))가 0 또는 1에 가까워지도록 유도하여, 각 wiehgt에 대한 Rounding(올림 또는 내림)을 명확하게 만드는 역할을 한다.

  • [β의 역할]

    • β가 큰 경우: 곡선이 완만하여 초기 단계에 h(V_{i,j}) 값이 0과 1사이로 자유롭게 조정될 수 있게함.
    • β가 작은 경우: 곡선이 매우 뾰족해져 h(V_{i,j})가 0 또는 1에 가까워지도록 강제. 최종 단계에서 이진화 촉진.

  • [Annealing 과정]
    최적화 과정 동안 β를 큰 값에서 작은 값으로 점진적으로 감소시킴.
    이를 통해 초기에는 가중치들이 자유롭게 조정되다가 점차 0 또는 1로 수렴됨.

---

2. '이전 layer들이 모두 quantized된 상태'를 현재 layer의 input으로 사용하여, 이전 층들의 Q 효과를 현재 층의 최적화에 반영하여 compensation한다.

최종 AdaRound 수식:

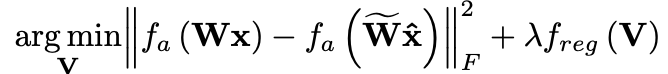
• $\bold{\hat{x}}$: layer's input with all preceding layers quantized

• $f_a$: activation function

• $f_a(\bold{Wx})$와 $f_a(\bold{\tilde{W}x})$의 차이를 최소화. 이는 quantized된 네트워크의 출력이 original 네트워크의 출력과 최대한 비슷하게 만듦.