"PTQ와 QAT 각각을 위한 standard pipeline을 제시하고 debugging workflow를 제안"

Quantization 효과

32bit 에서 8bit로 quantization 시,

Tensor를 저장하기 위한 memory overhead는 4배 감소.

Matrix multiplication을 위한 computational cost는 16($4^2$)배 감소

2. Quantization fundamentals

NN Quantization과 Quantized network가 동작하는 fixed-point accelerator의 기초 원리

2.1 Hardware background

NN accelerator의 두 가지 fundamental 요소

1. Processing elements $C_{n,m}$

2. accumulators $A_n$

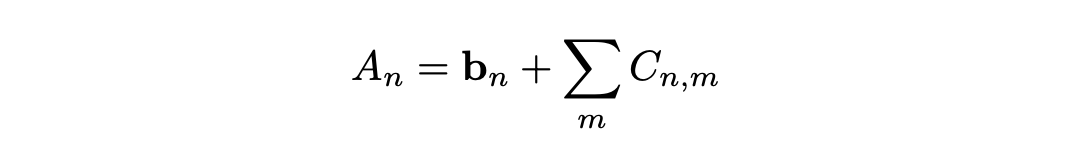
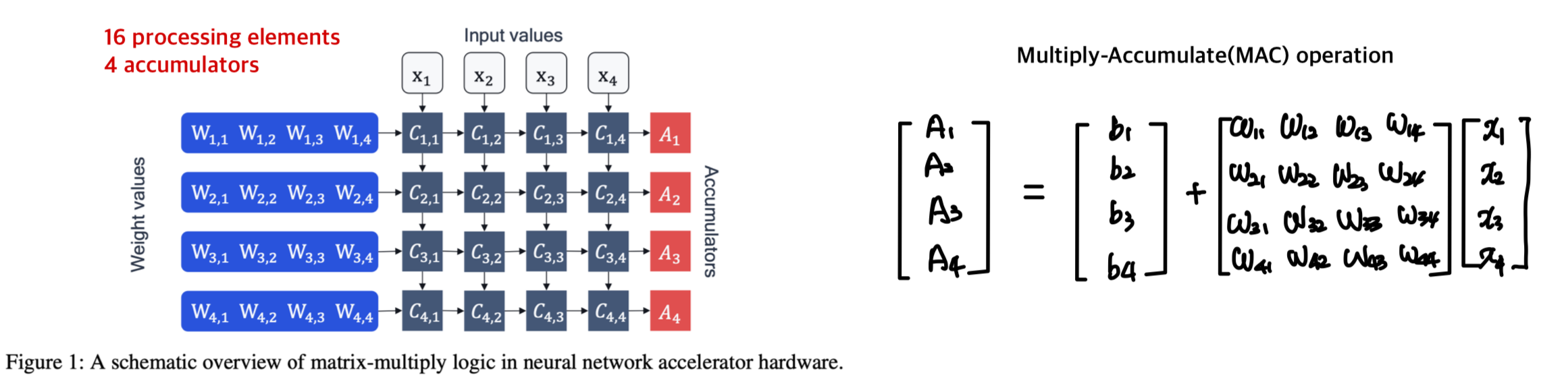
FP32로 inference 시, 32-bit data가 memory에서 processing units로 전달되야 한다.
MAC opeartion과 data transfer는 NN inference에 사용되는 energy의 대부분을 차지한다.

---

$\hat{\bold{x}}$ = $\bold{s}_\bold{x}$ $\cdot$ $\bold{x_{int}}$ $\approx$ $\bold{x}$ 일 때,
($\hat{\bold{x}}$ : quantized vector , $\bold{s}_\bold{x}$: FP scale factor, $\bold{x_{int}}$: INT vector)

weight와 activation을 quantize한 accumulation 수식은 다음과 같다.

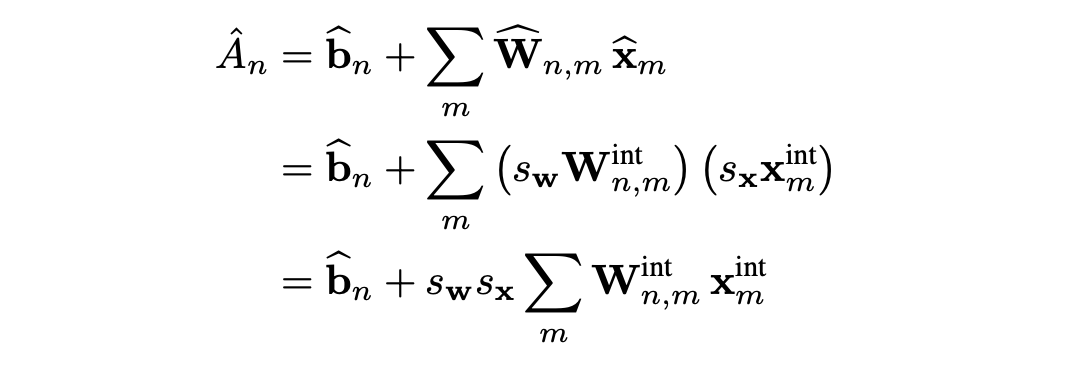
weight와 activation의 scale factor가 각각 $\bold{s_\bold{w}}$, $\bold{s_\bold{x}}$로 독립적으로 존재하는데, 이는 quantization error 줄이기 위함이다.

bias quantization의 경우 의도적으로 무시하는데, 이는 bias가 주로 higher bit-width(32-bits)에 저장되고, bias의 scale factor는 weights와 activations의 scale factor에 따라 조정돼기 때문이다.
(e.g. $\bold{s_{b}} =\bold{s_\bold{w}} \cdot \bold{s_\bold{x}}$)

---

Figure 2는 INT8 quantization을 적용했을 때 NN accelerator의 변화를 보여준다.
이때 accumulator는 higher bit-width(주로 32-bits)를 유지하는 것이 중요한데, 이유는
1. 누적기의 비트 폭이 작으면, 많은 곱셈 결과를 더할 때 값이 누적되어 오버플로우가 발생할 수 있기 때문이다.
2. 양자화된 연산에서는 작은 값들의 누적이 중요하므로, 충분한 비트 폭을 통해 정밀도를 유지해야 하기 때문이다.

32-bit accumulator에 저장된 activation은 다음 layer에 사용되기 전에 memory에 저장돼야 한다.
data transfer와 다음 layer의 복잡도를 줄이기 위해서, activation은 INT8로 다시 quantized 된다. 이 과정에서 requantization step이 필요하다.

2.2 Asymmetric Q

(=Uniform affine quantization)

quantization parameters: scale factor $s$, zero-point $z$, bit-width $b$

scale factor $s$: FP number, quantize의 step-size를 정한다.
zero-point $z$: real zero가 error 없이 quantized 되도록 한다.
zero padding이나 ReLU와 같은 연산들이 quantization error를 만들지 않도록 하는데 중요하다.

scaling
🔽
rounding -> rounding error
🔽
clipping -> clipping error: scale factor를 늘려 quantization range를 늘림으로써 clipping error를 줄일 수 있지만, 반대로 rounding error는 증가한다.

2.2.1 Symmetric Q

(=Symmetric uniform quantization)

symmetric quantization은 asymmetric case의 simplified version이다.
symmetric quantizer는 zero-point를 0으로 한다.

symmetric quantizer는 signed, unsigned quantization으로 나뉜다.

2.2.2 pow-of-2 Q

Power-of-two quantization은 symmetric quantization의 special case로,
scale factor가 $s=2^{-k}$ 형태이다.
bit-shifting에 대응되기 때문에 hardware 효율적이지만, 제한된 scale factor의 expressiveness로 rounding error와 clipping error 간의 trade-off를 악화시킬 수 있다.

2.2.3 Graularity(세분성)

• per-tensor quantization
  

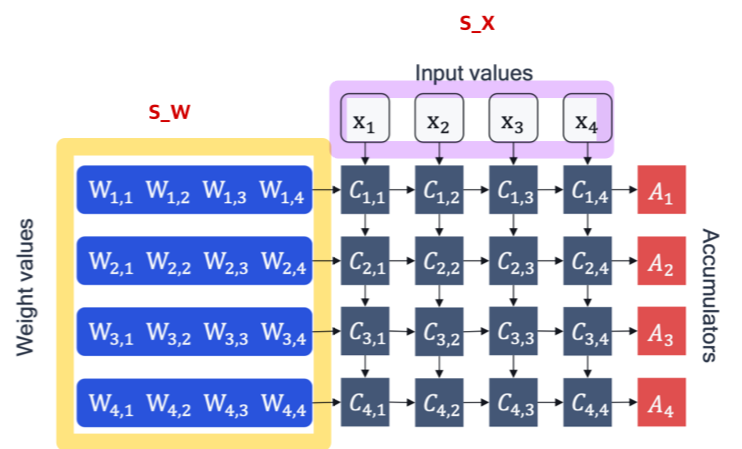
-weight tensor의 모든 weights에 대해 동일한 quantization parameter를 적용한다.
-모든 accumulator들이 동일한 scale factor $s_\bold{w}, s_\bold{x}$를 사용한다.
-단순한 hardware 구현이 가능해 가장 대중적인 방법이다.

---

• per-channel quantization
  

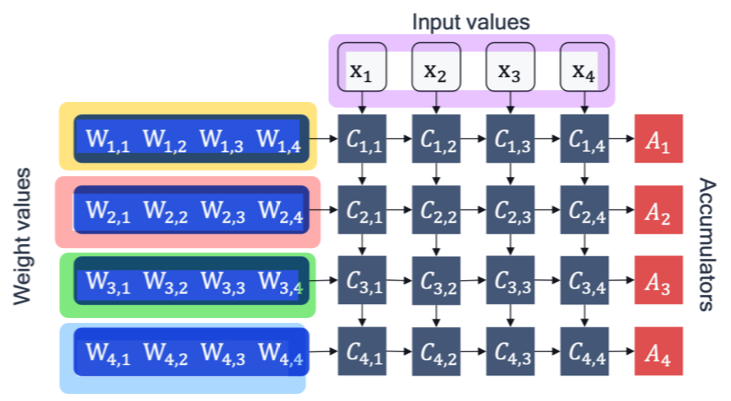
-tensor의 각 segment에 독립적인 quantization parameter를 적용한다.
-e.g. 각 output channel 마다 각기 다른 quantization parameter 적용.

---

• per-group quantization
  

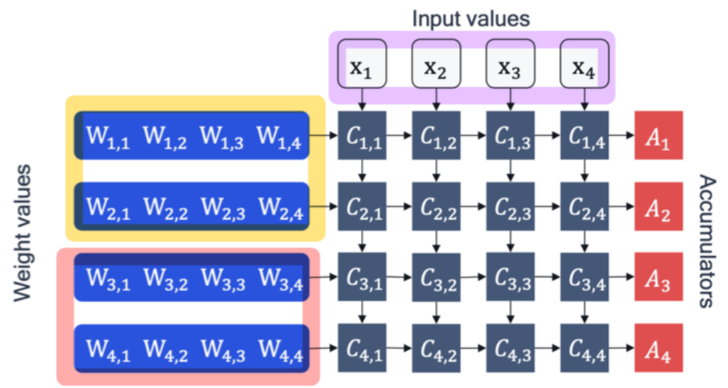
현존하는 대부분의 fixed-point accelerator들은 per-group quantization 방식을 지원하진 않는다. 미래엔 더 많은 hardware support가 있다면 가능할 수도 있겠다.

---

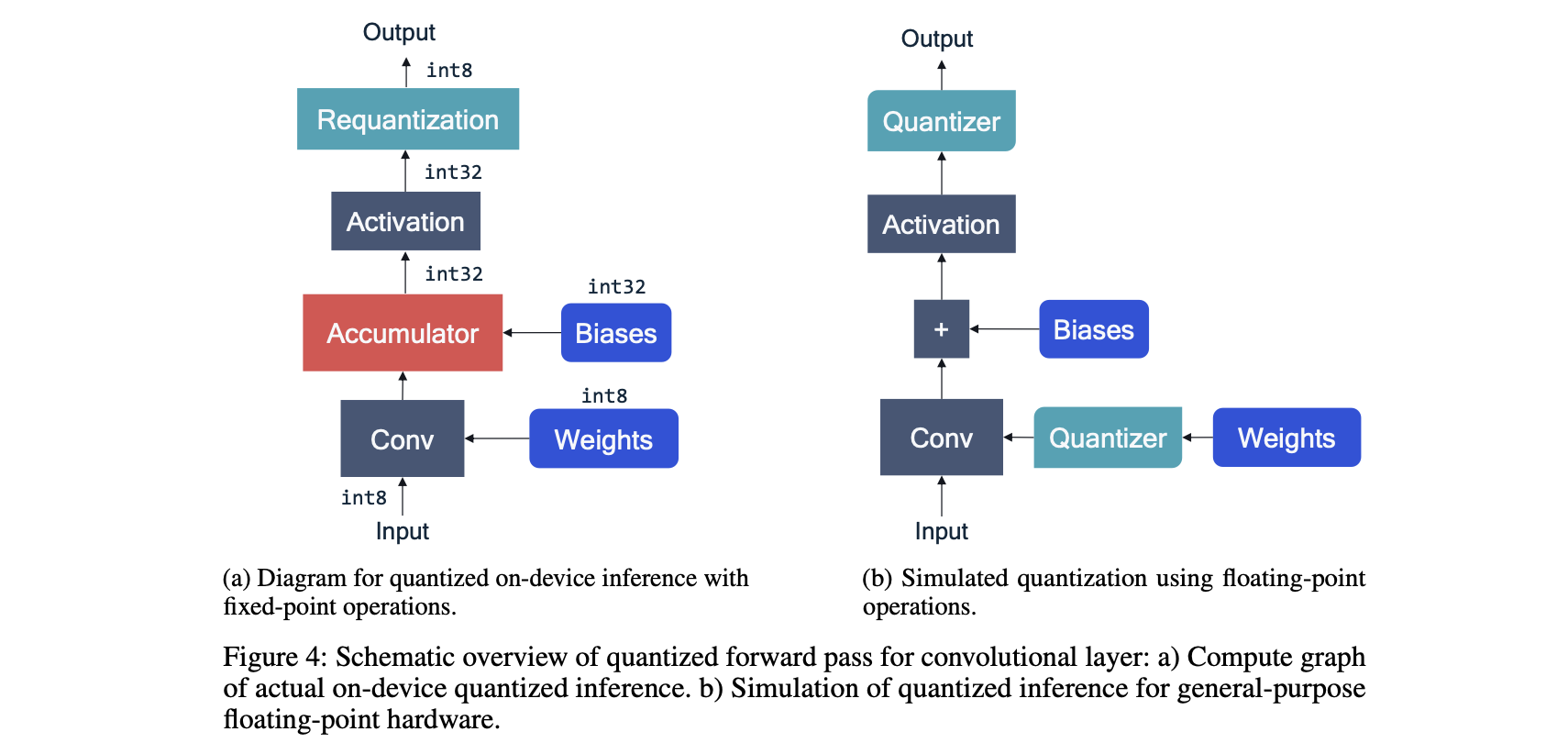
2.3 Q simulation

FP hardware를 이용해 fixed-point 연산을 시뮬레이션 하는 것을 의미한다.

Figure 4 (a)는 fixed-point hardware에서 동작하는 과정이고,
(b)는 동일한 convolutional layer가 DL framework로 모델링된 과정이다.
weight quantization을 시뮬레이션 하기 위한 weight quantizer block과
activation quantization을 시뮬레이션 하기 위한 activation quantizer block이 추가 됐다.
bias의 경우 주로 quantized되지 않고 higher-precision으로 저장된다.

2.3.1 BN folding

Batch normalization(BN)은 현대 CNN의 standard component이다.

$\mu, \sigma$: training 과정에서 학습된 batch 평균, 분산
$\gamma, \beta$: 정규화된 값을 조정하기 위해 학습된 scale, shift, parameter

• training 단계에서는 배치 정규화가 입력을 정규화하여 학습을 안정화시킨다.
• 그러나 inference 단계에서는 학습된 평균과 분산을 사용하여 정규화하면 충분하다.
• 따라서, on-device inference 단계에서 BN 연산을 수행하지 않기 위해, BN 연산을 network에서 제거하고, 이를 인접한 linear layer로 흡수한다.

만약 BN이 linear layer 직후 적용된다면 $\bold{y} = \text{BatchNorm}(\bold{Wx})$,
BN이 linear layer 자체에 fused 되도록 수식을 바꿀 수 있다.

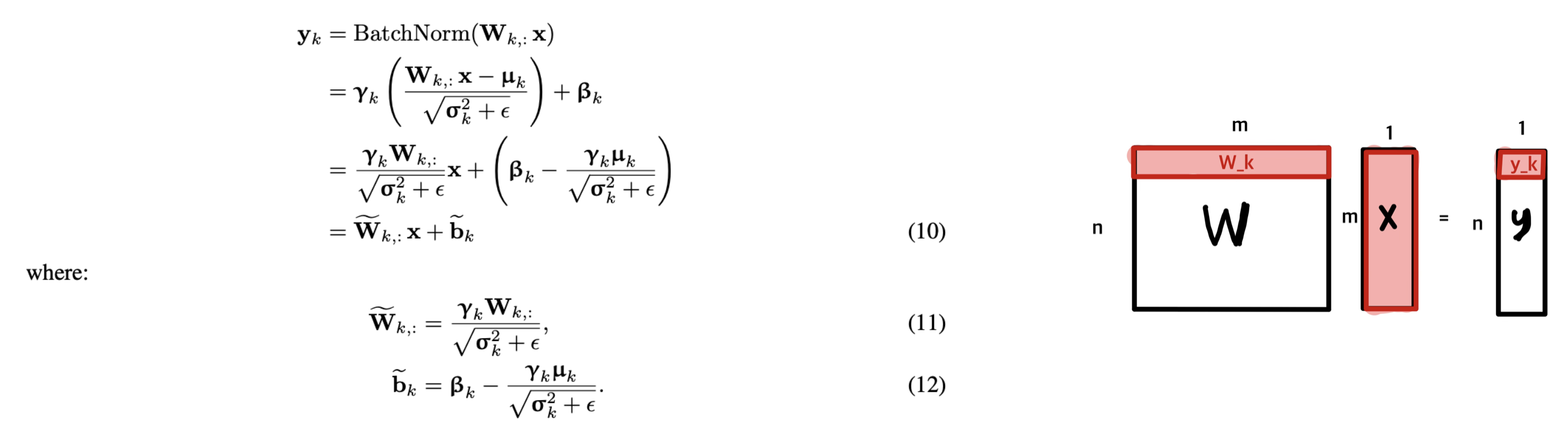
2.3.2 Act. func fusing

• 기존 방법 => 두 단계의 메모리 입출력으로 불필요한 overhead 초래

  STEP 1. 선형 연산: 𝑌 =𝑊⋅𝑋+𝑏
  STEP 2. quantization
  STEP 3. 결과 Y를 메모리에 저장.
  STEP 4. 메모리에서 𝑌를 로드.
  STEP 5. 비선형 활성화 함수 적용: 𝑓(𝑌)
  STEP 6. quantization

이 경우, linear layer의 activation을 memory에 저장하고, 다시 non-linearlity를 적용하기 위해 memory에서 load 해야 한다.

이런 이유로, 많은 hardware solution에선 requantization step 이전에 non-linearlity를 적용하는 hardware unit을 갖는다.

• Activation function fusing => 메모리에 저장하는 단계 제거

  STEP 1. 선형 연산 결과에 바로 비선형 활성화 함수 적용: 𝑓(𝑊⋅𝑋+𝑏)
  STEP 2. quantization

이 경우, non-linearlity 이후 requantization만 simulation 하면 된다.

sigmoid 또는 Swish 같은 복잡한 activation 함수의 경우, 위와 같은 fusing이 지원 되지 않는다면, non-linearity 이전, 이후에 quantization step을 추가해야 한다.
그런데 이는 quantized 된 모델의 accuracy에 큰 영향을 미칠 수 있다.
Swish function과 같은 새로운 activation이 FP에선 accuracy를 향상하더라도, quantization 이후 fixed-point hardware에 적용하는데에는 오히려 성능이 더 악회될 수 있다.

2.3.3 Other layers (Guide)

• Max pooling
  activation quantization이 요구되지 않는다. 왜냐하면 input과 ouput value가 동일한 quantization grid 상에 있기 때문이다.

• Average pooling
  interger의 average는 integer가 아닐 수 있다. 따라서, quantization이 필요하다.
  하지만, 저자의 경우 inputs와 outputs에 동일한 quantizer를 사용하는데, quantization range가 크게 변하지 않기 때문이다.

• Element-wise addition
  정확하게 quantization simulation 하기 어려운 연산이다.
  addition 되는 두 input의 quantization range가 정확하게 일치해야 하는데,
  만약 일치하지 않으면, network가 공유되는 quantization parameter를 갖도록 optimize 하는 등 추가적인 작업이 요구된다.

• Concatenation
  역시 concat되는 두 input이 동일한 quantization parameter를 갖지 않기 때문에,
  network가 공유되는 quantization parameter를 갖도록 optimize 하는 것이 필요할 수 있다.

2.4 Practical considerations

multiple layer들로 구성된 NN을 quantize할 때, quantization scheme, granularity, bit-width를 포함한 large space of quantization choice들을 마주하게 된다.
이 문단에선 search space를 줄이는데 도움을 줄 수 있는 사항들을 제시한다.

여기선 보편적인 hardware가 지원하는 homogeneous bit-width만 다룬다.
(weight와 activation에 적용된 bit-width가 모든 layer에 걸쳐 동일하다.)

heteorgeneous bit-width 또는 mixed-precision의 구현에 관한 연구가 존재하기도 한다.
Mixed precision dnns: All you need is a good parametrization
HAWQ: hessian aware quantization of neural networks with mixed-precision
Bayesian bits: Unifying quantization and pruning

2.4.1 Scheme: Symmetric vs Asymmetric Q

asymmetric quantization은 추가적으로 offset parameter를 갖기 때문에, 더 expressive한 반면에, computational overhead가 발생할 수 있다.

asymmetric weights $\bold{\hat{W}} = s_\bold{w}(\bold{W_{\text{int}}}-z_{\bold{w}})$를 asymmetric activations $\hat{\bold{x}} = s_{\bold{x}}(\bold{x_\text{int}}-z_\bold{x})$와 곱했을 때를 생각해보자.

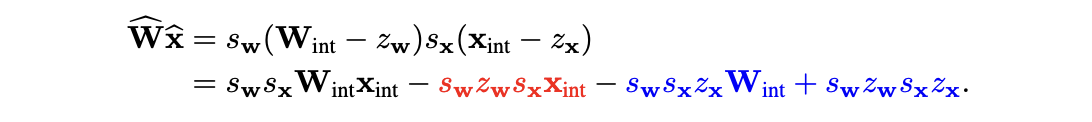
$\footnotesize \textcolor{black}{첫 \ 번째 \ term}$: symmetric Q와 asymmetric Q 모두 공통적으로 갖는다.

$\footnotesize \textcolor{blue}{세 \ 번째, 네 \ 번째 \ term}$: 미리 알고 있는 scale, offset, weight values로 구성되어 있어 추가적인 cost가 들지 않는다.

$\footnotesize \textcolor{red}{두 번째 \ term}$: input data $\bold{x}$가 들어있기 때문에, inference 시점에 각 data의 batch마다 이 term을 추가적으로 연산해야 한다.
이는 추가적인 channel을 더하는 것과 동등하므로, latency와 paower에 큰 overhaed가 발생할 수 있다.

이런 이유로, symmetric weight quantization과 asymmetric activation quantization을 사용해서 추가적인 data-dependent term을 피하는 것이 보편적인 접근법이다.

2.4.2 Granularity: Per-tensor and per-channel Q

weight와 activation의 per-tensor quantization은 모든 fixed-point accelerator들이 지원하기 때문에 standard로 사용됐다.

weight을 per-channel quantization
하지만, 특히 weight의 distribution이 channel마다 크게 vary한 경우, weight의 per-channel quantization이 accuracy를 향상할 수 있다. 따라서 실전에서 점점 보편적으로 사용되고 있다.

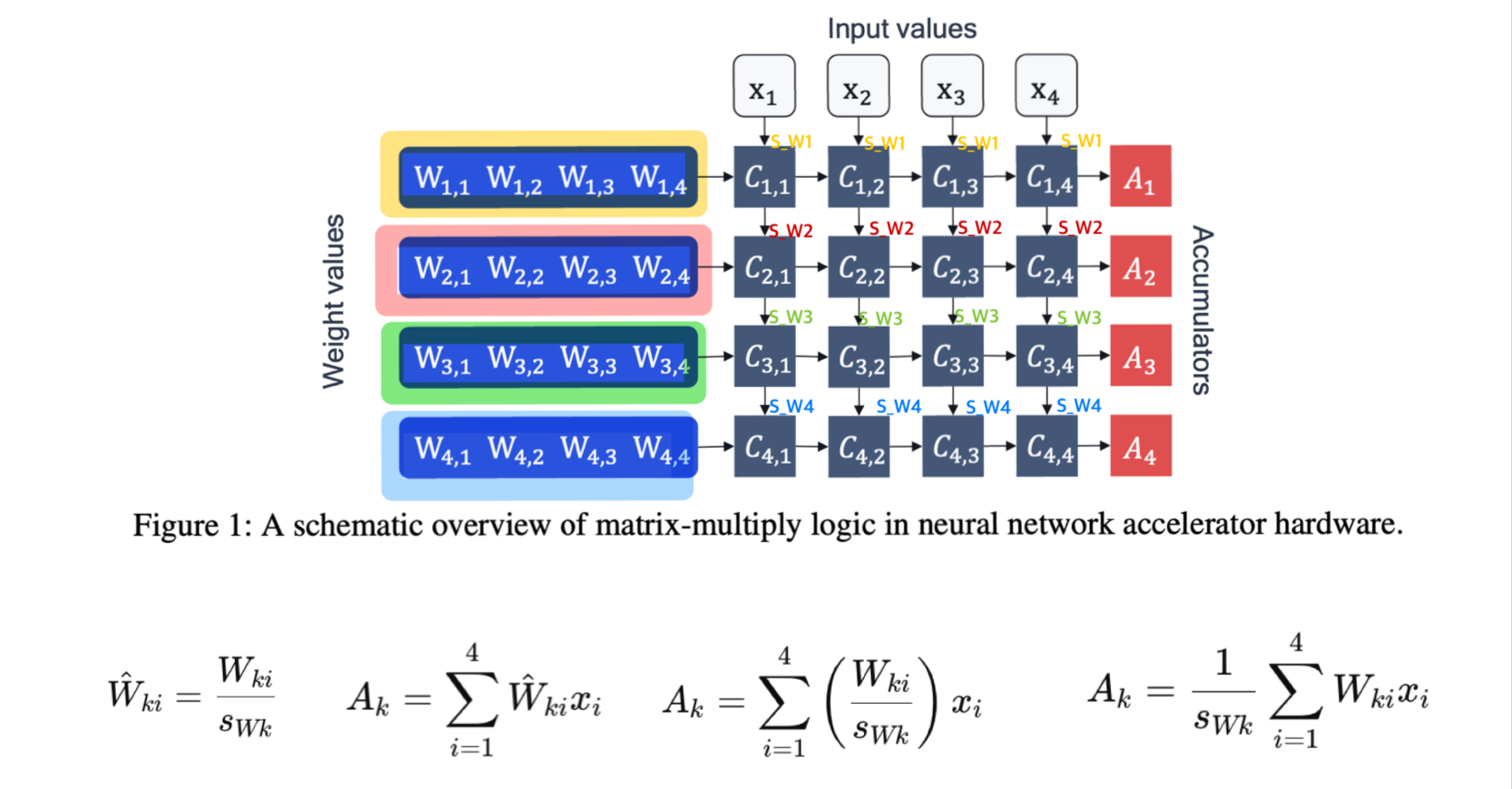
activation을 per-channel quantization
반면, activation의 per-channel quantization의 경우 구현이 훨씬 힘들다.

그 이유는 $A_k$를 계산할 때, 각 channel 마다의 scale factor($s_{X_1}, s_{X_2}, s_{X_3}, s_{X_4}$)를 사용하기 때문이다.
즉, 서로 다른 기준으로 scaling 된 값들을 단순히 summation 하면, 일관되지 않은 결과를 초래할 수 있기 때문에, 각 input channel 마다 다른 scale factor를 고려해 줘야 한다.

(반면, weight의 경우 $A_k$를 계산할 때, scale factor가 공통으로 같으므로($s_{W_k}$) 연산이 훨씬 간단하다.)

3. PTQ

PTQ 과정의 fundamental step은 각 quantizer에 최적의 quantization range를 찾는 것이다.

3.1 Q range setting

quantization의 clipping threshold $q_{min}, q_{max}$를 찾는 것.

quantization range setting의 key
1. clipping error와 rounding error 사이의 trade-off
2. clipping range가 각 quantizer의 final task loss에 미치는 영향
: PTQ는 각 layer에서의 quantization error를 줄이는데 집중하므로,
모델의 최종적인 목표(분류 등)의 Loss에 미치는 영향을 잘 고려해야 한다.

Weight는 calibration data 없이 quantization이 가능하지만,
activation quantization의 parameter를 정하기 위해선 주로 a few batches of calibration data가 필요하다.

Min-max

$q_{min} = \text{min}\bold{V}, q_{max} = \text{max}\bold{V}$

$\bold{V}$: original vector

• 장점: clipping error X
• 단점: outlier에 sensitive하여, 과도한 rounding error 유발 가능.

MSE(Mean squared Error)

original tensor와 quantized tensor 간의 MES를 최소화하는 $q_{min}, q_{max}$를 찾는다.

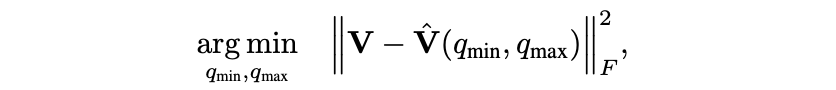
$\bold{V}$: original vector, $\bold{\hat{V}}(q_{min}, q_{max})$: quantized version of $\bold{V}$

주로 grid search, golden section method, anayltical approximations with closed-form solution 방법 등을 사용해 위의 optimization problem을 푼다.
Post training 4-bit quantization of convolutional networks for rapid-deployment

장점: 매우 큰 outlier 문제를 피할 수 있다.

Cross entropy(CE)

MSE의 경우, tensor의 모든 값에 동일한 가중치를 부여하여 양자화 오류를 최소화하기 때문에, 중요한 large value에서 큰 양자화 오류가 발생할 수 있다.

하지만 특정 layer, 예를 들어, classification network의 경우, quantize할 tensor의 모든 value들의 중요도가 다른 경우가 존재한다.
마지막 layer의 tensor를 구성하는 logit들의 경우, 많은 value들의 크기가 작거나 negative인 logit들이 존재하게 되는데, 사실상 accuracy에 영향을 크게 미치는 크기가 큰 value들의 order( 어떤 class에 해당하는지)를 quantization 이후에도 유지하는 것이 중요하다.

이런 경우, quantization range를 구하기 위해선 CE를 사용한다.

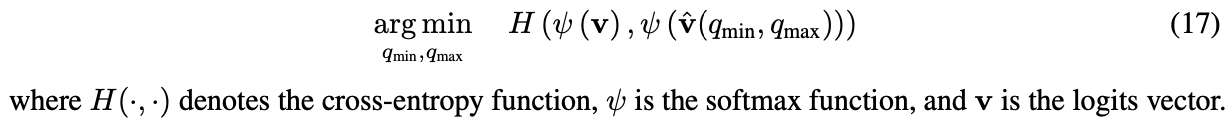
BN based range setting
BN activation을 갖는 layer라면,
BN 과정에서 학습한 shift parameter $\beta$는 per-channel 의 mean,
BN 과정에서 학습한 scale parameter $\gamma$는 per-channel의 standard deviation과 같다.

(BN은 input data를 평균이 0이고 분산이 1인 형태로 정규화한 후, 학습 가능한 𝛾와 𝛽를 사용해 다시 scaling하고 shift한다.
학습된 𝛾는 각 channel data의 scale(표준 편차)을 반영하며,
𝛽는 각 channel의 데이터의 shift(평균)를 반영하기 때문이다.)

shift parameter $\beta$와 scale parameter $\gamma$는 activation quantizer의 적합한 parameter를 찾는데 사용될 수 있다.
Up or Down? Adaptive Rounding for Post-Training Quantization

---

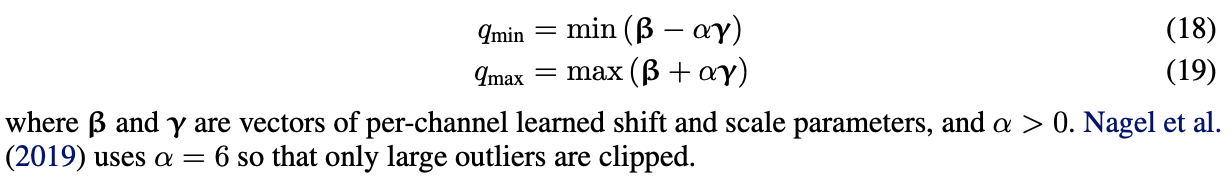
비교

weight quantizaion에서 range setting 방법들을 비교했다.
1. high bit-widths에선 MSE와 min-max 접근이 유사하지만, lower bit-widths에선 MSE가 min-max보다 분명하게 out-perform 함을 알 수 있다.

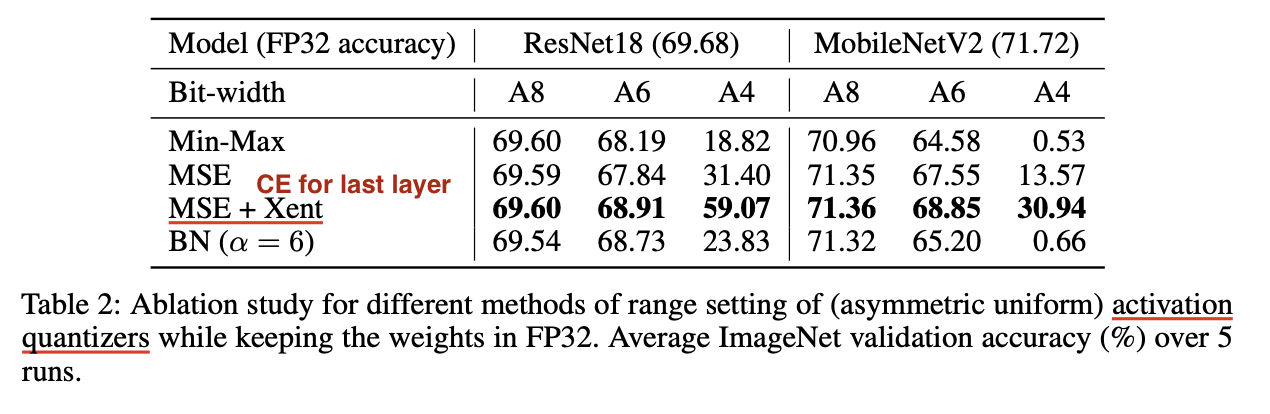
activation quantization에서 range setting을 비교했다.
1. MSE + Xent(마지막 layer에 CE 사용)이 다른 방법들보다 out-perform 함을 알 수 있다.
2. 마지막 layer에 MSE를 쓰는 것보다 CE를 쓰는게 더 이득임을 알 수 있다.

3.2 CLE

"cross-layer equalization(CLE)은 연속적인 layer들의 dynamic range들을 조정해 유사하게 만들어, quantization error를 최소화하는 scaling factor $\bold{s}_i$를 찾는 방법이다."

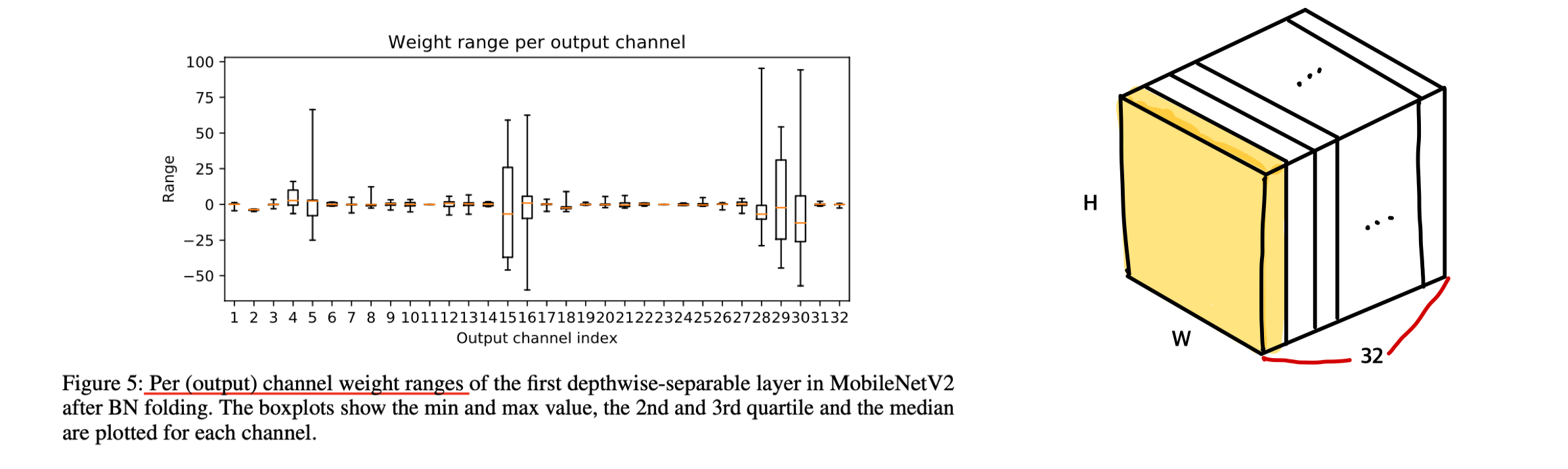
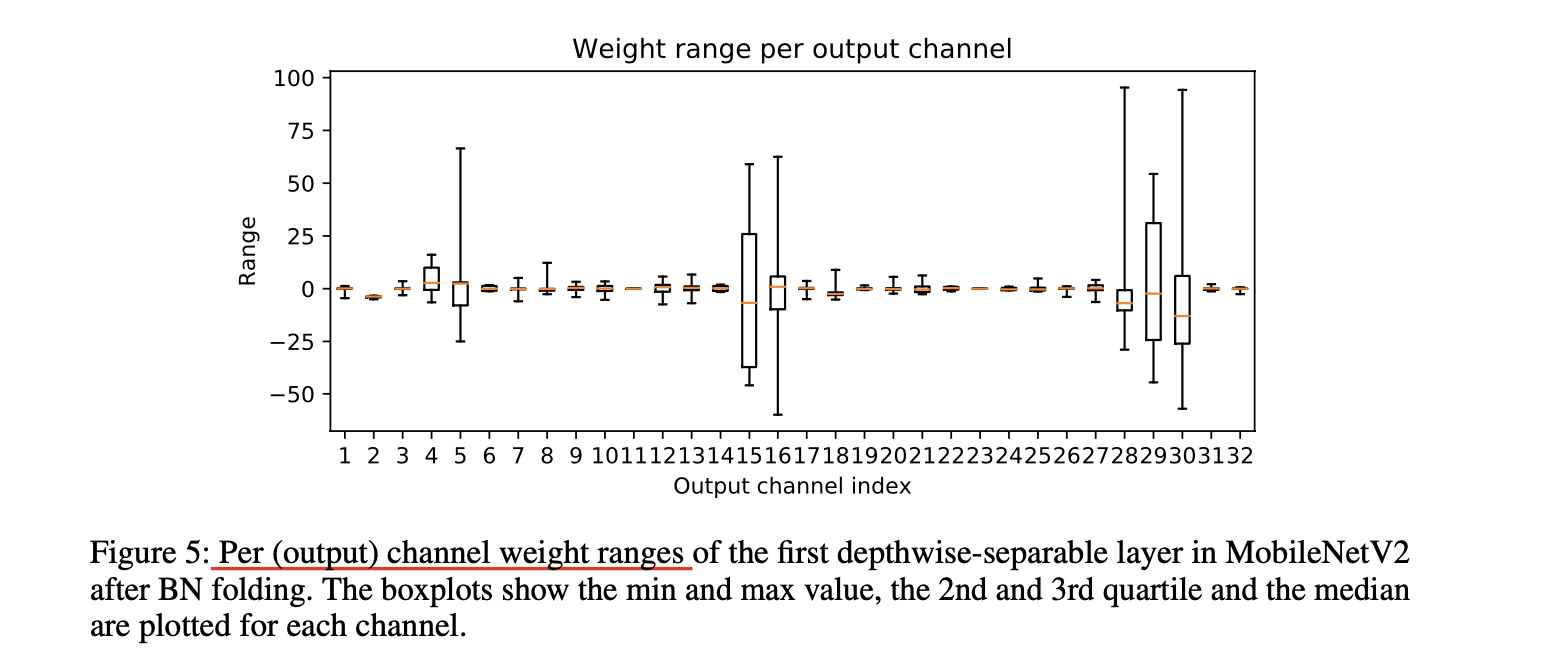
depth-wise separable layer(e.g. MobileNet)들의 경우, 몇몇 weight들이 각 output feature를 담당하기 때문에, weight들이 variability가 큰 문제가 있다.
이런 경우, clipping error와 rounding error 사이의 적합한 trade-off를 찾기 어렵다.

BN folding은 이 문제를 악화시켜, 다양한 output channel에 연결된 weight들 간의 strong imbalance를 초래한다. 특히, per-channel quantization과 같은 fine-graned quantization 보다 per-tensor quantization에 문제가 되는 경우가 많다.

이러한 imbalance 문제를 해결하기 위한 solution은 activation function(e.g, ReLU, PreLU)이 positive scaling equivariance를 가진다는 점에 기반한다.

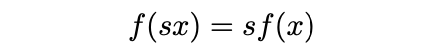
$s$: non-negative real number
(1차 homogeneous function도 이를 만족하며, ReLU6와 같이 구간별 선형 함수를 parameter를 조절하여 scaling하는 piece-wise linear function(여러 구간으로 나누어 각 구간마다 다른 선형 함수를 사용하는 함수)도 이 equivariance를 만족한다.)

신경망의 연속적인 layer에 positive scaling equivariance를 활용하면 다음과 같다.
두 layer $\bold{h} = f(\bold{W}^{(1)}\bold{x} + \bold{b}^{(1)})$, $\bold{y} = f(\bold{W}^{(2)}\bold{h} + \bold{b}^{(2)})$가 주어질 때,

cross-layer equalization(CLE)는 연속적인 layer들의 dynamic range들을 조정해 유사하게 만들어, quantization noise를 최소화하는 scaling factor $\bold{s}_i$를 아래와 같이 찾는다.

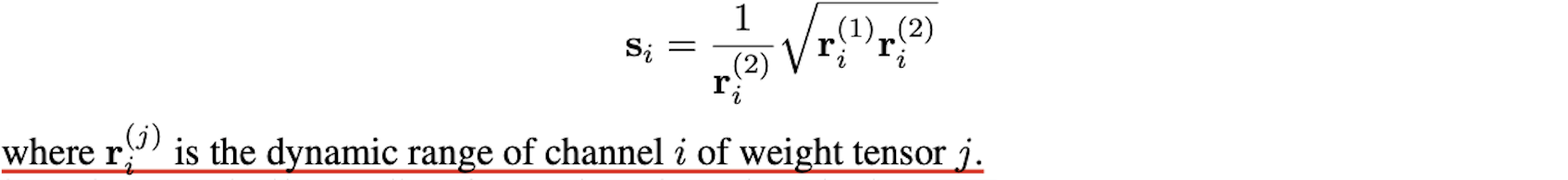
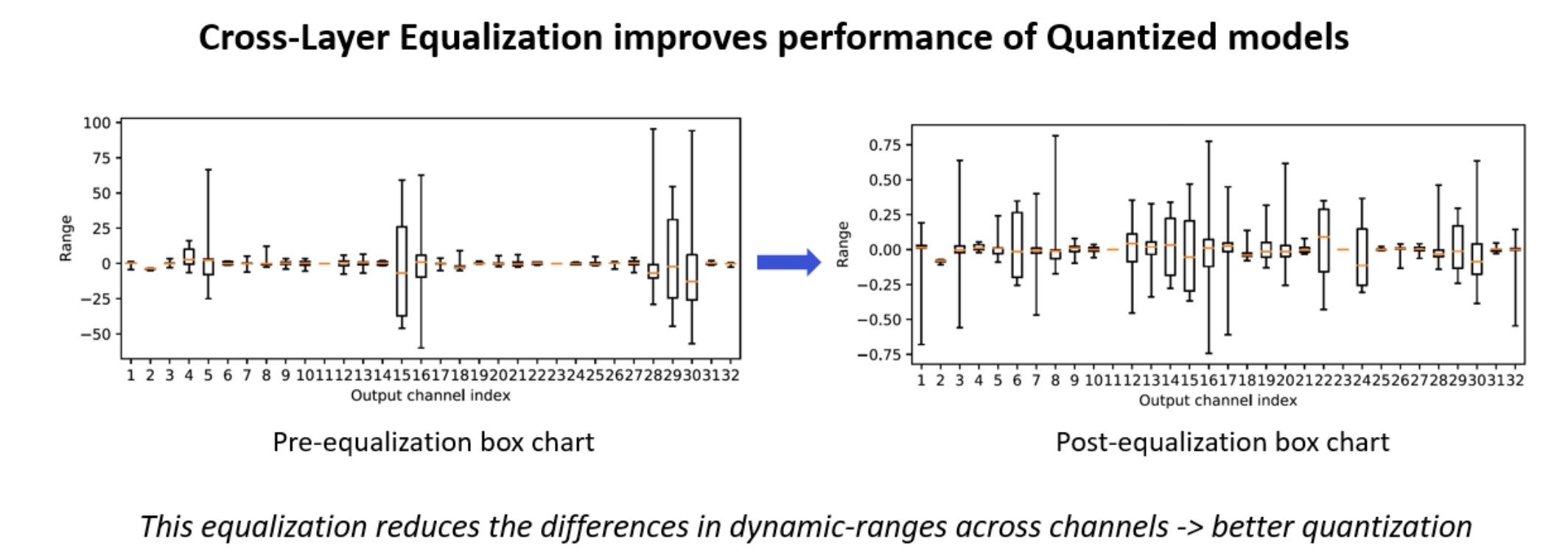
Absorbing high biases

CLE 이후, high biases는 activation의 dynamic range를 크게 바꿔버리는 문제가 발생할 수 있다.
이 문제를 해결하기 위해, 가능하다면 high biases를 다음 layer로 흡수하는 방법을 제안했다.

• STEP 1
  다음과 같은 reparameterization을 통해, ReLU 함수 $f$ 이전에 통과하는 layer 1의 $\bold{c}$를 layer 2로 흡수한다.

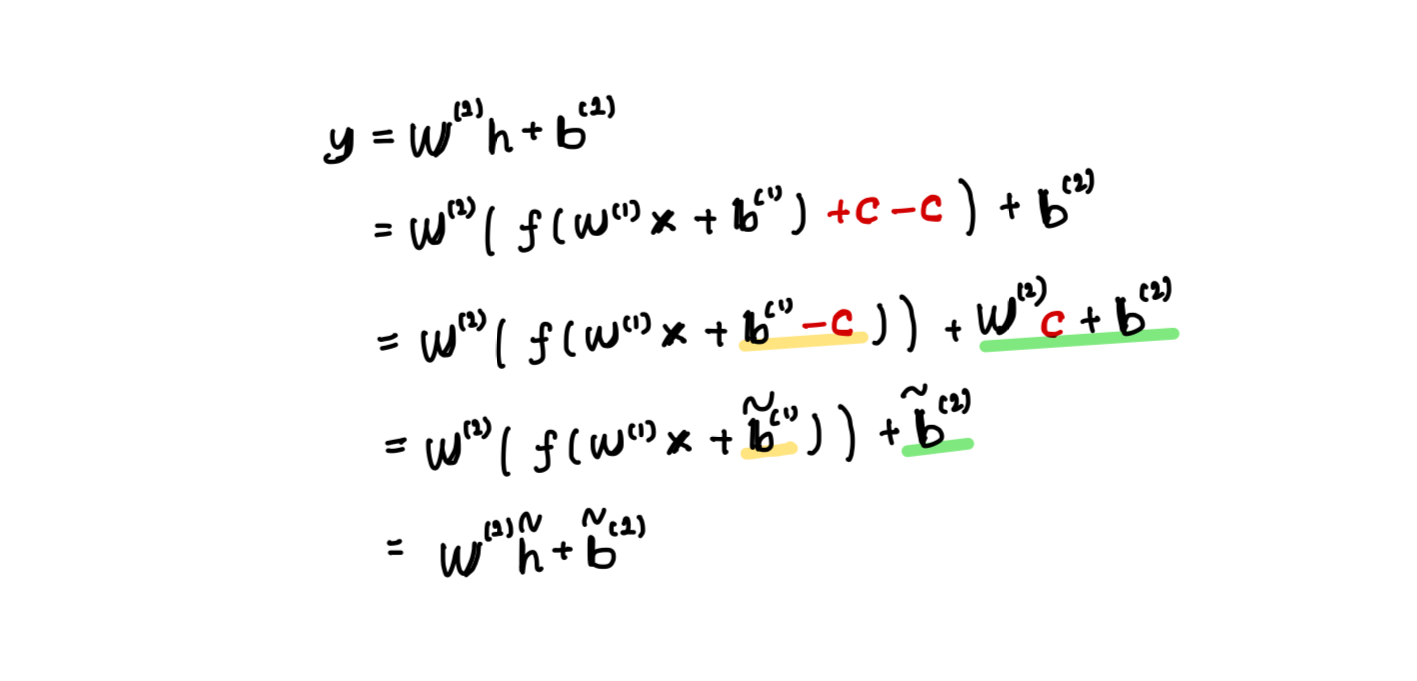
• STEP 2: $\bold{c}$ 구하기
  ReLU function $f$가 있는 layer에 대해서, $r(\bold{Wx + b - c}) = r(\bold{Wx + b}) - \bold{c}$를 만족하는 non-negative vector $\bold{c}$가 존재한다는 사실을 이용한다.

trivial solution $\bold{c=0}$은 모든 $\bold{x}$에 대해 성립한다.

하지만, $\bold{x}$의 distribution과 $\bold{W}$, $\bold{b}$의 value에 따라, empirical distribution의 거의 모든 $\bold{x}$에 대해 $\bold{c}_i > 0$ value는 다음과 같이 존재할 수 있다.

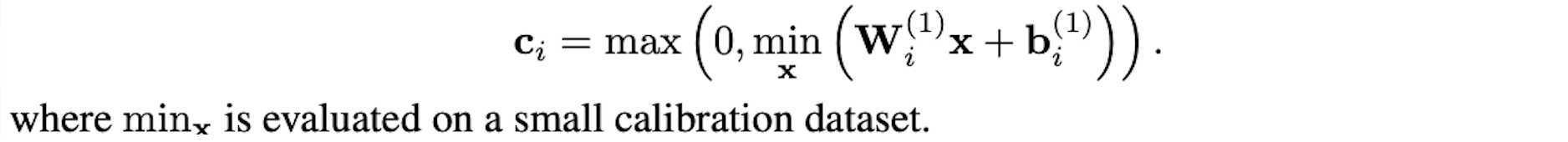
data에 대한 dependency를 제거하기 위한 방법으로, 저자는 위 equation의 우항을 BN layer의 shift, scale parameter로 estimation하는 방법을 제시했다.

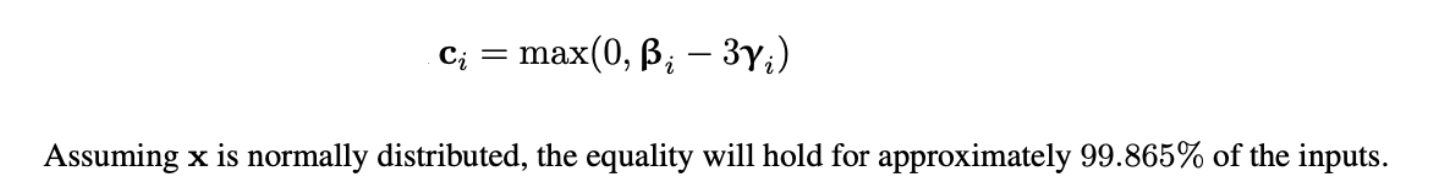
Experiments

CLE와 bias absortion가 MobileNetV2의 8-bit quantizing에 미치는 영향을 실험했다.
skip-connection은 layer 사이의 equivariance를 break하기 때문에, 오직 residual block 안의 layer들에 대해 CLE를 적용했다.

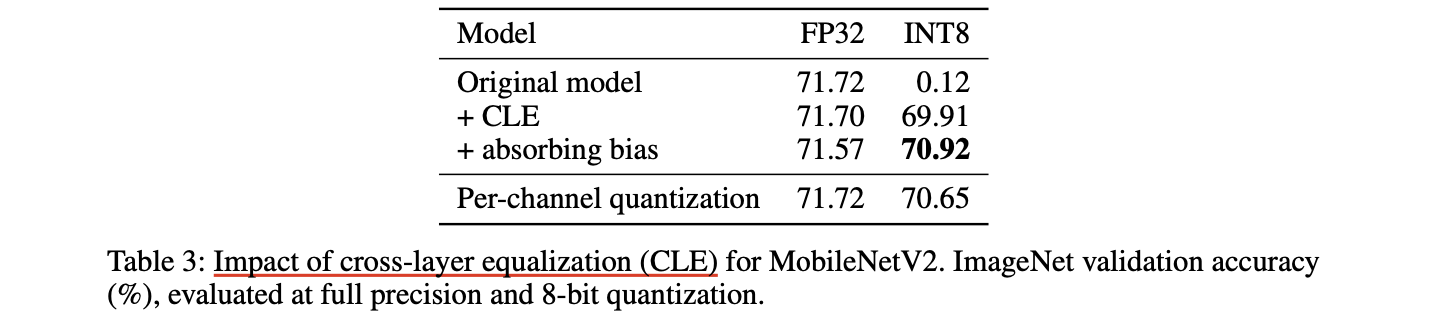
absorbing high biases는 FP32 성능에서 하락을 보였다. 이는 approximation이기 때문인데, 더욱 정확한 activation quantization으로 quantized performance를 1% 향상할 수 있었다.

per-tensor quantization 이후 CLE와 bias absorption을 함께 사용하는 것이 per-channel quantiation 보다 좋은 성능을 보였다.

3.3 Bias correction

quantization error가 biased 되는 문제(expected output of the original and quantized layer is shifted)도 빈번하게 발생한다.

$\mathbb{E}[\bold{Wx}] \neq \mathbb{E}[\bold{\hat{W}x}]$

이러한 error는 각 output channel이 몇몇의 원소로 구성된(3x3 kernel에 9개) depth-wise separable layer에서 두드러진다.
clipping error가 주 원인이며, clipped된 outlier가 평균 distribution을 shift 하곤 한다.

distribution의 expected shift를 바로잡기 위한 방법들이 제시됐다.
quantized layer $\mathbb{E}[\bold{Wx}]$와 quantization error $\Delta{\bold{W}}=\bold{\hat{W} - W}$에 대해서,
expected output distribution은 다음과 같다.

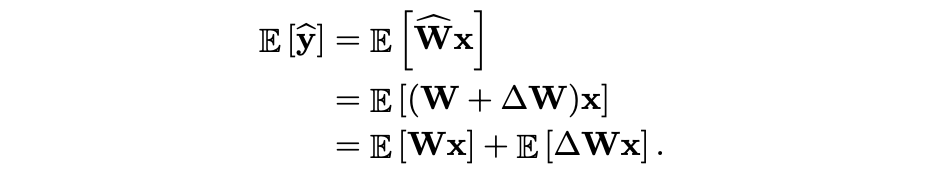
biased error는 $\mathbb{E}[\Delta \bold{Wx}]$이고, 상수이기 때문에 $\Delta \bold{W{\mathbb{E}[\bold{x}]}}$와 같고,
이 값이 0이 아니면 output distribution이 shifted 된다.
따라서 이를 output에서 빼줌으로써 shift를 바로잡는다.

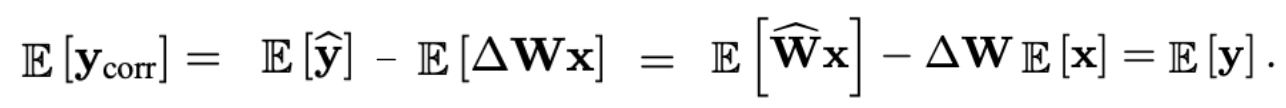
이 correction term은 bias와 같은 shape을 가지므로, inference 시점에 추가적인 overhead 없이 bias에 흡수될 수 있다.
bias correction term $\Delta \bold{W{\mathbb{E}[\bold{x}]}}$을 계산하는 방법은 여러가지가 있지만, 가장 흔하게 사용되는 두 가지 방법은 empirical bias correction과 analytical bias correction 방법이다.

Empirical bias correction

calibration dataset에 접근할 수 있다면, bias correction term은 단순히 FP 모델과 quantized 모델의 activation을 비교해서 계산할 수 있다. 실전에선, layer-wise로 다음을 계산한다.

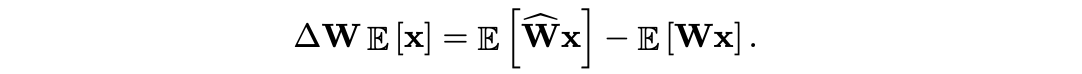
Analytic bias correction

BN과 ReLU 함수를 사용하는 경우, data에 접근하지 않고 BN의 statistics를 이용해 expected input distribution $\mathbb{E}[\bold{x}]$를 계산할 수 있다.

Experiments

MobileNetV2를 8-bit로 quantize할 때 bias correction의 효과를 증명했다.

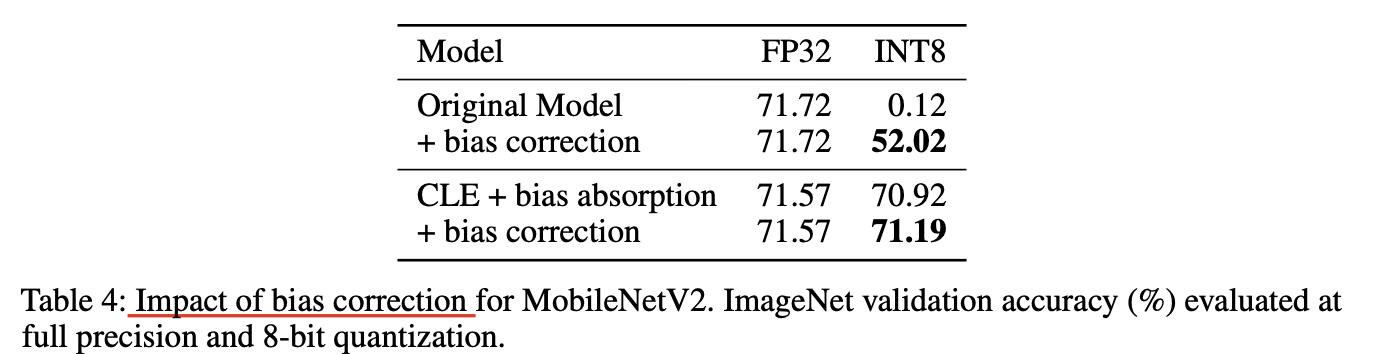
anaytical bias correction은 quantized 모델의 성능을 random ~ 50% 이상까지 향상했는데, 이를 통해 quantization에 의한 biased error가 모델의 성능을 크게 떨어뜨림을 알 수 있다.

bias correction을 CLE와 같이 사용했을 때, 상호 보완적이 었으며, 어떠한 data를 사용하지 않고도 FP32 성능에 가까운 성능을 달성했다.

3.4 AdaRound

"AdaRound는 weight가 rounded되는 방식을 optimize하여, quantization 과정에서 final task loss에 영향을 최소화하기 위한 방법이다."

NN weight는 각 FP32 value를 nearest quantization grid point로 projecting해서 quantized 된다.
이 방식을 rounding-to-nearest 방식이라고 부르며, 이 방식은 FP와 quantized weight 사이의 MSE를 최소화 한다.

반면, PTQ에서 final task loss를 줄이는 관점에서 rounding-to-nearest는 weight를 quantize하는데 optimal 하지 않음을 밝히는 연구가 제시됐다.
저자는 아래 Figure 7와 같이, ResNet18의 first layer를 100 가지 다른 stochastic rounding sample들을 사용해 4 bits로 quantize하고 각 rounding choice에 대해 network의 성능을 평가했다.
그 결과, best rounding choice는 rounding-to-nearest 방식보다 10% 이상 성능이 좋음을 알 수 있었다.

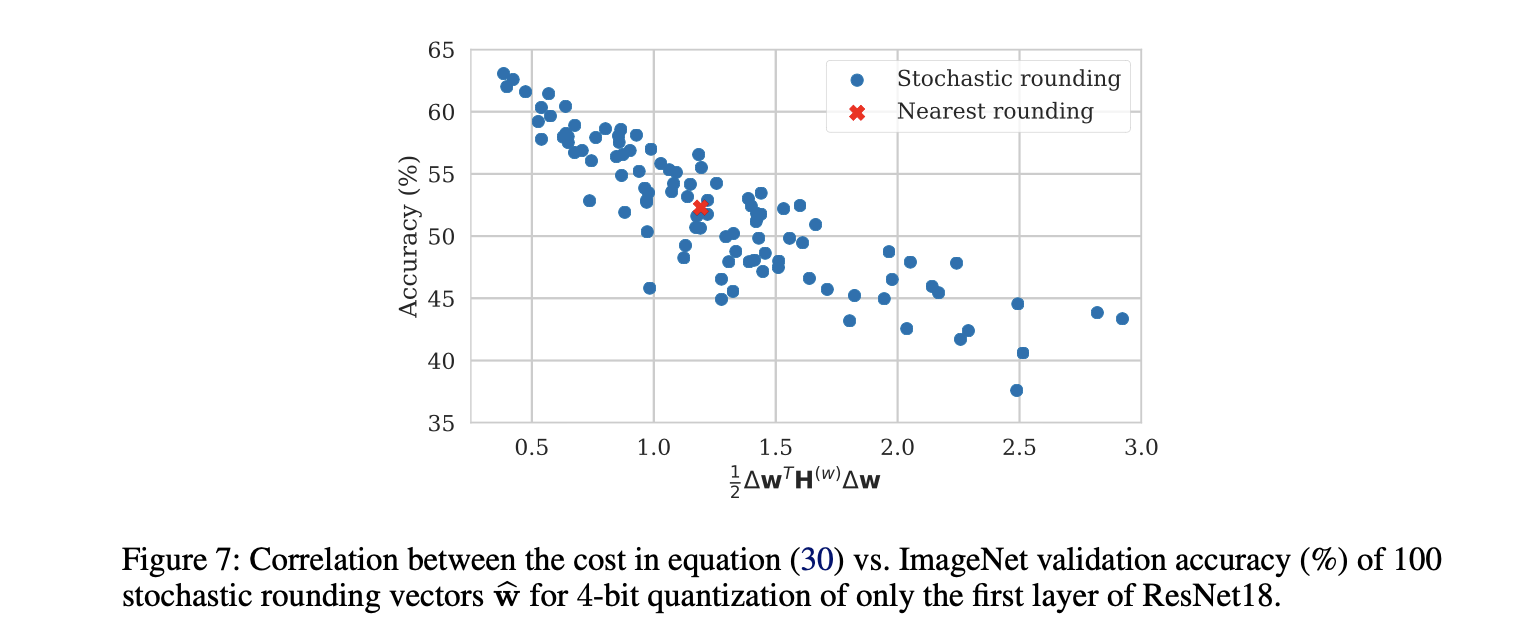
여기선 PTQ에서 weight rounding choice를 잘 찾기 위한 AdaRound 방법을 살펴본다.

여기서 main goal은 final task loss에 quantization의 영향을 최소화 하는 것이기 때문에, optimization 문제를 loss로 다음과 같이 수식화할 수 있다.

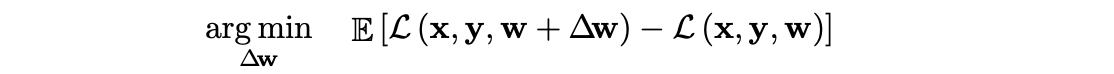
∆w는 quantization으로 인한 변화를 나타내며, 각 weight에 대해 두 가지 가능한 값을 가질 수 있는데, 하나는 weight를 올림(rounding up)한 값이고 다른 하나는 가중치를 내림(rounding down)한 값이다.

우리는 이 binary optimization 문제(올림할지, 내림할지)를 효율적으로 풀고 싶다.

모든 가능한 rounding choice에 대해 성능을 평가하는 것은 계산적으로 매우 비효율적이므로, 이를 간소화하기 위해 테일러 급수를 사용하여, 모델의 loss 변화를 근사적으로 계산할 수 있다.

2차 테일러 급수 확장(second-order Taylor series expansion)을 사용해 cost function 𝐿(𝑥,𝑦,𝑤)를 Δ𝑤에 대해 근사한다. 이를 통해 직접적인 성능 평가 없이 손실 변화를 예측할 수 있다.

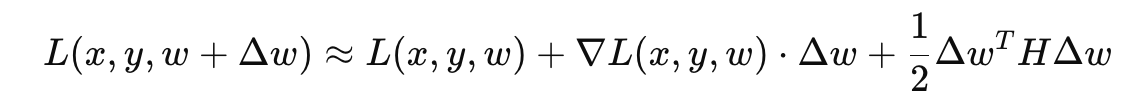
∇𝐿(𝑥,𝑦,𝑤)는 loss function의 gradient, 𝐻는 Hessian 행렬이다.

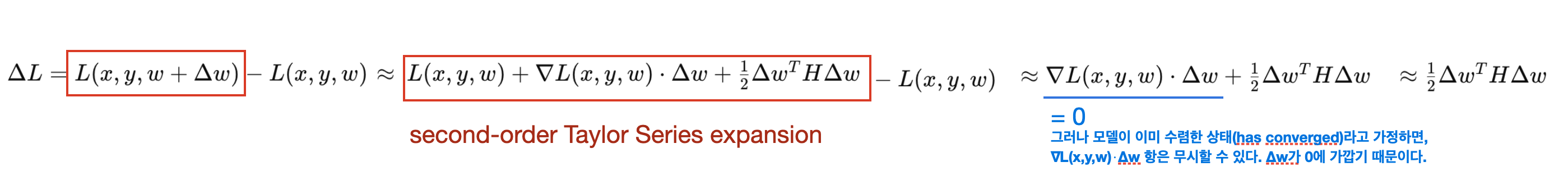
결과적으로, 다음의 Hessian based 2차 unconstrained binary optimization (QUBO) problem을 푸는 것과 같다.

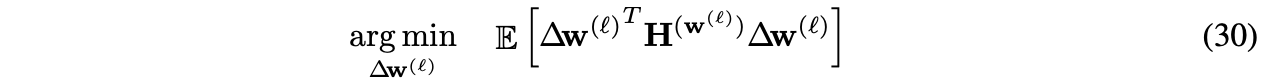
하지만, 위 수식 (30) 은 두 가지 이유로 인해 weight rounding에 널리 적용되는데 어려움이 있다.

문제 1. Hessian을 계산하는 것은 memory, computational complexity가 크므로 보편적인 use-case에 적합하지 않다.

문제 2. 위 수식 (30)은 NP-Hard 이다. (해를 찾는 것이 매우 어렵다.)

문제 1을 해결하기 위해서, 저자는 추가적인 가정을 도입해, 수식 (30)을 다음과 같이 layer의 output activation의 MSE를 최소화하는 local optimization problem으로 단순화 한다.

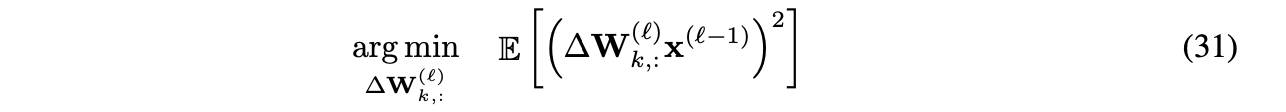
수식 (31)은 Hessian 연산이나 하위 layer들로부터의 backward, forward propagation이 요구되지 않는다.
하지만, 여전히 수식(31)은 NP-hard optimization problem인 문제가 존재한다.

reasonable한 computational complexity로 approximate할 수 있는 solution을 찾기 위해, 저자는 다음과 같은 continuous optimization problem으로 단순화한다.

수식 (32) 역시 regularizer term을 도입해 continuous optimization variables $h(\bold{V}_{i,j})$ 가 0 또는 1로 converge하도록 하여, 수식 (31)의 discrete optimization의 valid solution이 되도록 한다.

저자가 사용한 regularizer는 다음과 같다.

network의 여러 layer에 걸친 error accumulation을 방지하고 non-linearity을 고려하기 위해, 저자는 다음과 같은 final optimization problem을 제안했다. 이를 AdaRound라고 부른다.

요약하면, quantization 과정에서 weight를 rounding하는 것은 network의 성능에 큰 영향을 미친다.
AdaRound는 이론적으로 탄탄하고, 연산적으로 빠른 weight rounding 방법이다.
AdaRound는 오직 적은 양의 unlabeled data sample들만 필요하고, hyperparameter tuning이나 end-to-end finetuning이 필요 없으므로, FCN, CNN과 같은 어떤 NN에도 적용 가능하다.

3.5 Standard PTQ pipeline

computer vision 및 NLP 모델에 좋은 결과를 보인, PTQ를 위한 best-practice pipeline을 제시한다.
모델에 따라 어떤 단계는 필요하지 않을 수 있고, 또는 다른 방법을 사용하는 것이 더 좋은 성능이 될 수 있다.

CLE(Cross-layer equalization)

• FP 모델을 quantization friendly하게 pre-processing 하는 단계이다.
• 특히 depth-wise separable layer들과 per-tensor quantization에 중요하다.

Add quantizer

• target HW에 따라 quantizer 선택은 달라질 수 있다.
• 보통의 AI accelerator의 경우, weight는 symmetric quantizer로, activation은 asymmetric quantizer를 사용하는 것을 추천한다.
• 만약 HW/SW stack이 지원한다면, weight는 per-channel quantization을 사용하는 것이 좋다.

Weight range setting

• 모든 weight tensor들의 quantization parameter를 setting하기 위해서, layer-wise MSE based criteria를 사용하는 것을 추천한다.
• per-channel quantization의 경우, min-max 방법을 사용하는 것이 좋은 경우도 있다.

AdaRound

• 조금의 calibration dataset을 갖고 있다면, weight의 rounding을 optimize하기 위해 AdaRound를 적용한다.
• 이 단계는 low-bit(e.g. 4 bits) PTQ의 경우 매우 중요하다.

Bias correction

• calibration dataset이 없고, network가 BN을 사용한다면, analytical bias correction을 대신 사용할 수 있다.

Activation range setting

• 마지막 단계로, network의 모든 data-dependent tensor (i.e., activations)의 quantization range를 결정한다.
• 대부분의 layer에 MSE 기반의 criteria를 사용한다. 이는 minimum MSE loss를 찾기 위해 작은 calibration dataset만 요구된다.
• 이 대신, data-free pipeline의 경우 BN 기반의 range setting을 사용할 수 있다.

3.6 Experiments

PTQ pipeline을 CV와 NLP에 적용해 성능을 평가했다.

• Semantic Segmentation
  model: DeepLabV3 (with MobileNetV2 backbone)
  dataset: Pascal VOC

• Object Detection
  model: EfficientDet
  dataset: COCO 2017

• Image Classification
  model: ResNet18, ResNet50, MobileNetV2, InceptionV3, EfficientNet lite
  dataset: ImageNet

• Natural Language Understanding
  model: BERT-base
  dataset: GLUE benchmark

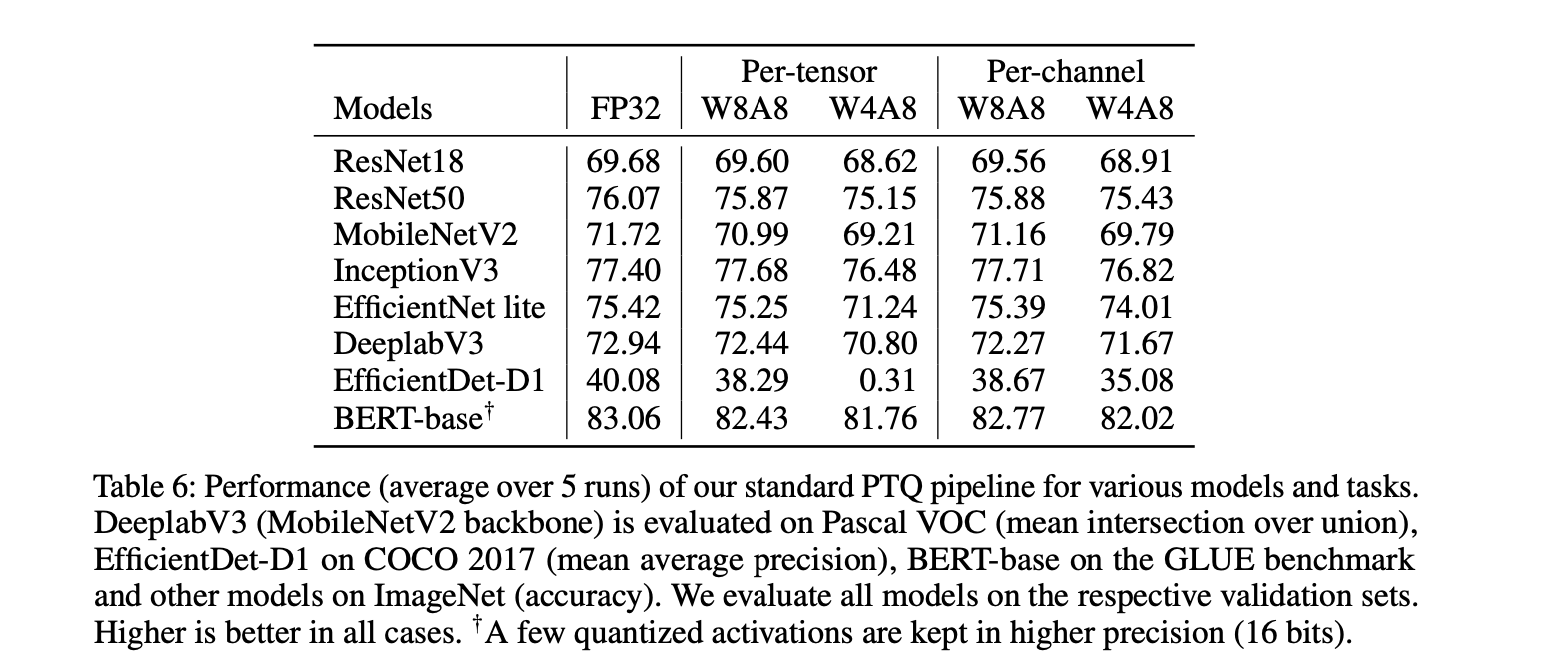
W8A8
모든 모델이 FP와 비교해서 accurracy drop이 0.7% 이내이다.
per-channel quantization을 사용해서 얻은 이득이 크지 않다.

W4A8
per-channel quantization을 사용해서 얻은 이득이 꽤 있다.

depth-wise separable convolution -> per-channel quantization
ResNet18, ResNet50, InceptionV3의 경우, accuracy drop이 per-tensor인 경우와 per-channel quantization인 경우 모두 FP의 1% 이내이다.
그런데, 더 efficient한 network인 MobileNetV2, EfficientNet lite는 per-tensor quantization의 경우 각각 2.5%, 4.2%로 drop이 증가한다.
이는 depth-wise separable convolution의 quantization으로 발생했을 가능성이 높다.
따라서 여기선 per-channel quantization을 사용하면 큰 이득을 얻을 수 있는데,
EfficientNet lite의 per-channel quantization은 per-tensor quantization에 비해 accruacy가 2.8% 증가했고, FP와 비교했을 때 drop이 1.4% 이내이다.
backbone에서 depth-wise separable convolution을 사용하는 EfficientDet-D1, DeeplabV3 에서도 유사한 효과를 볼 수 있었다.

BERT-base 모델의 경우, 몇몇의 activation tensor가 extreme하게 다른 dynamic range를 가짐을 관찰할 수 있었다. PTQ가 동작하게 하기 위해서, 저자는 다음 3.7절의 debugging 절차에 따라 해당 layer들을 16bit로 유지했다.
다른 모델들과 거의 비슷한 경향을 보였고, 4 bit weight quantization을 PTQ pipeline으로 구현하여, GLUE score에서 1.5% 이내의 drop을 보였다.

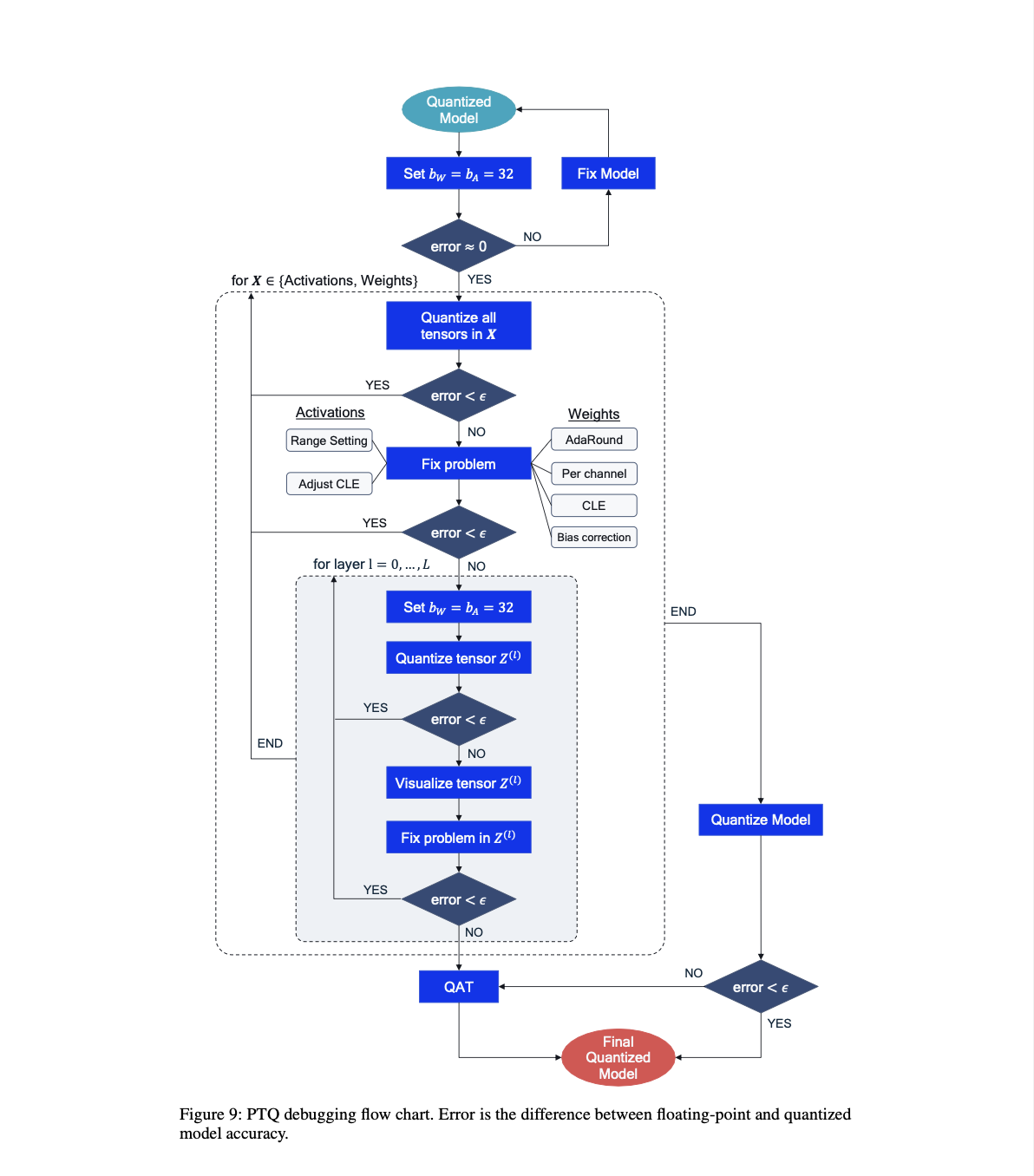
3.7 Debugging

standard PTQ pipeline을 따를 때, 모델의 성능이 잘 나오지 않는다면, bottleneck을 찾고 성능을 향상하기 위한 단계를 제안한다.
디버깅 절차는 왜 quantized된 모델이 성능이 잘 나오지 않는지에 대한 insight와 문제 해결에 도움이 될 수 있다.

STEP 1. FP32 sanity check
FP 모델과 quantized 모델이 forward pass에서 유사하게 동작하는지를 확인하는 것이 중요하다.
quantized 모델의 weight와 activation의 bit-width를 32bits로 설정하고, FP32 모델의 accuracy와 일치하는지 체크한다.

STEP 2. Weights or activations quantization
다음 단계는 weight 또는 activation quantization 각각이 어떻게 성능에 영향을 미치는지 확인한다.
weight를 high bit, activation을 low bit로 또는 activation을 high bit, weight를 low bit로 해서 각각의 상대적인 성능 drop 영향을 체크한다.

STEP 3-1. Fixing weight quantization
만약 STEP 2에서 weight quantization이 accruacy drop에 큰 영향을 준다면, 몇 가지 시도해볼 solution이 있다.

• CLE를 적용해본다. 특히 depth-wise separable convolutions를 갖는 모델일 경우!

• per-channel quantization을 시도해본다. 이는 uneven한 per-channel weight distribution의 문제를 해결할 수 있다.

• bias correction 또는 calibration data 사용이 가능하면 AdaRound를 적용본다.

STEP 3-2. Fixing activation quantization

만약 STEP 2에서 activation quantization이 accruacy drop에 큰 영향을 준다면,

• 각기 다른 range setting 방법을 시도해 본다.

• CLE를 조정해서 activation quantization range를 조절한다.
  vanilla CLE는 uneven activation distribution을 초래할 수 있기 때문이다.

STEP 4. Per-layer analysis
만약 global solution을 적용해도 accuracy drop이 너무 크다면.. 각 quantizer를 독립적으로 체크해 본다.
각 quantizer를 sequential하게 target bit-width로 + 나머지 network는 32 bits로 setting 한다.

STEP 5. Visualizing layers
만약 각 독립적인 tensor의 quantization이 큰 accruacy drop을 유발한다면,
각기 다른 granularity(per-channel in Figure 5), dimension(per-token or per-embedding for activations in BERT)으로 tensor distribution을 visualizing 해보는 것을 추천한다.

STEP 6. Fixing individual quantizers

visualization step에선 tensor의 quantization에 대한 sensitivity를 발결할 수 있다.
흔한 solution은
1. quantizer의 custom range setting
2. 문제가 되는 quantizer를 higher bit-width로 허용하는 것이다.
만약 문제가 해결되고 accuracy가 회복되면, 다음 quantizer로 넘어가고,
그렇지 않다면 QAT와 같은 다른 방법을 사용해봐야 할 것이다.

위 과정을 모두 완료하면, 마지막 STEP은 desired bit-width로 모델을 완성하는 것이다.
만약 accuracy가 너무 떨어진다 싶으면..
1. higher bit-widths 고려
2. 더 작은 granularity 사용
3. 다른 더 좋은 quantization 방법(QAT 같은) 사용

---

4. QAT

PTQ는 구현이 용이하고, labeled data로 network를 retraining할 필요가 없지만,
activation을 4 bit 이하 low-bit로 quantization 할 때 한계가 존재한다.

QAT는 더 긴 training, labeled data, hyper-parameter search가 요구되지만,
training 과정에서 quantization noise source를 모델링하여, PTQ보다 더욱 optimal한 solution을 제공한다.

4.1 Simulating Q for backward path

quantized된 network를 training을 위해, back-propagation이 필요한데,
quantization 수식의 gradient는 0 또는 undefined이기에 training이 불가능한 문제가 있다.

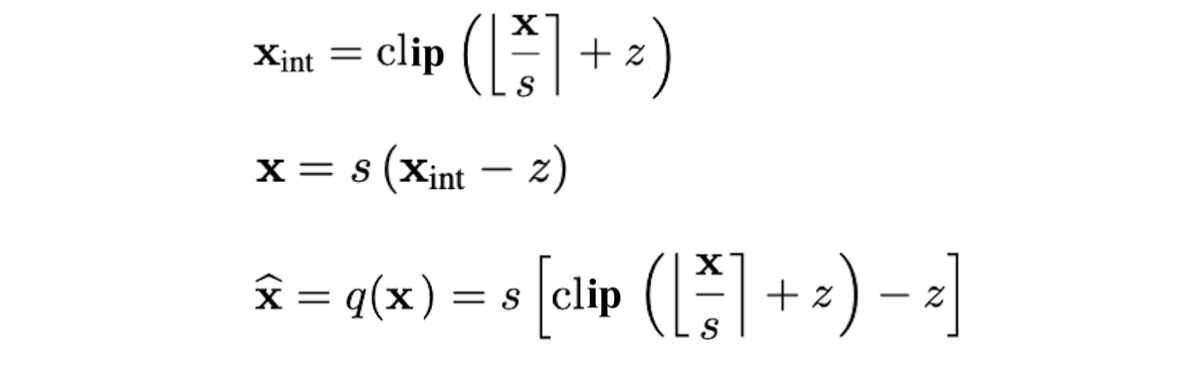
이 문제를 해결하기 위해서 STE(straight-through estimator)를 이용해 rounding operation의 gradient를 1로 approximation하는 방법을 사용하여, quantization operation의 graident를 계산한다.

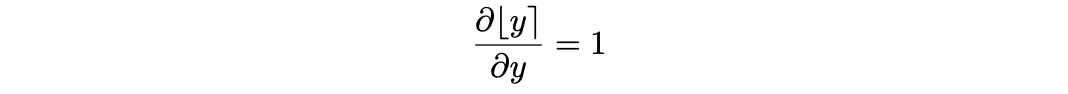
$z=0$인 symmetric quantizatoin 상황을 가정하고, (asymmetric quantization도 $z$는 constant이기 때문에, 결과는 동일하다)
$n=q_{min}/s, p=q_{max/s}$로 integer grid limit를 정의하자. input $\bold{x}_i$에 대한 quantization 수식의 gradient는 다음과 같이 구할 수 있다.

QAT에서의 forward pass와 backward pass를 간단하게 computational graph로 나타내면 다음과 같다.

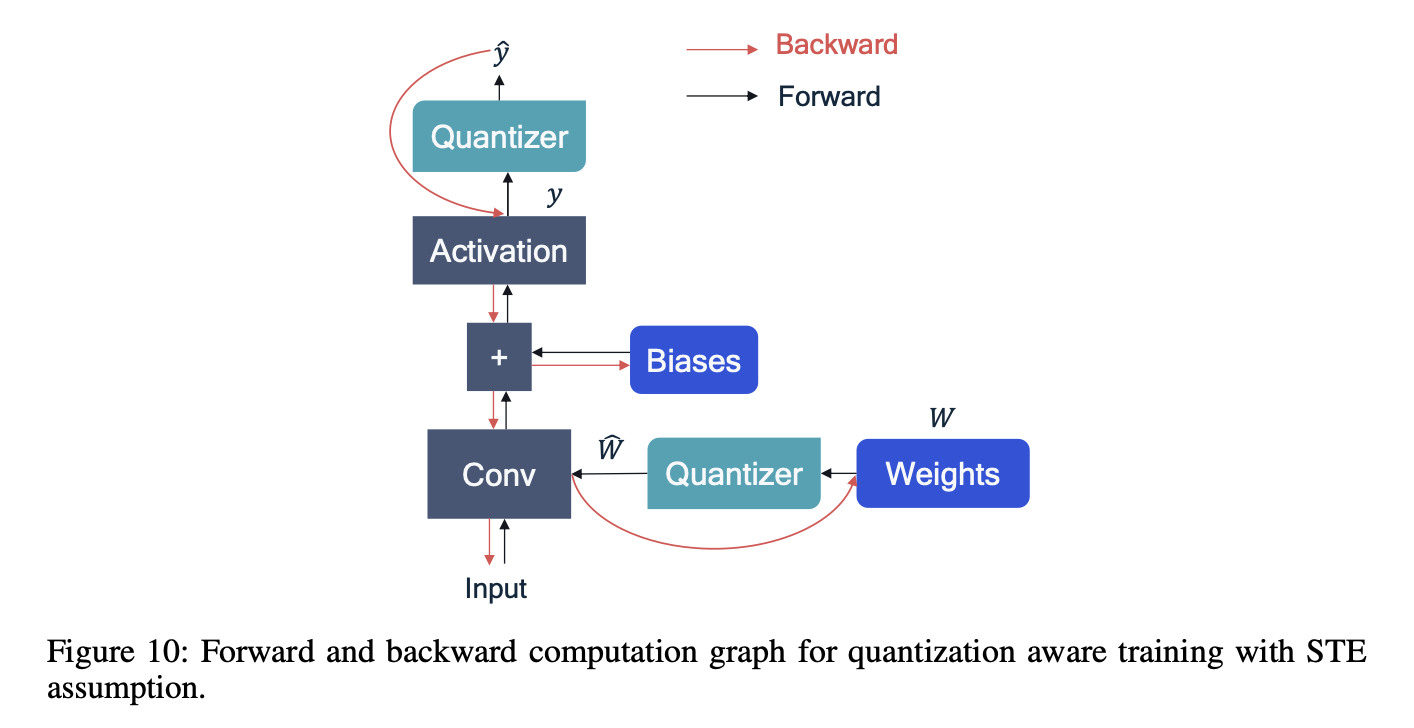
QAT 연구 초기에는 weight와 activation의 quantization range는 주로 min-max range 방법을 사용해 각 iteration마다 update했다.
이후 연구에선, STE를 사용해 quantization parameter인 $z, s$에 대해 gradient를 계산한다.

gradient w.r.t. scale factor

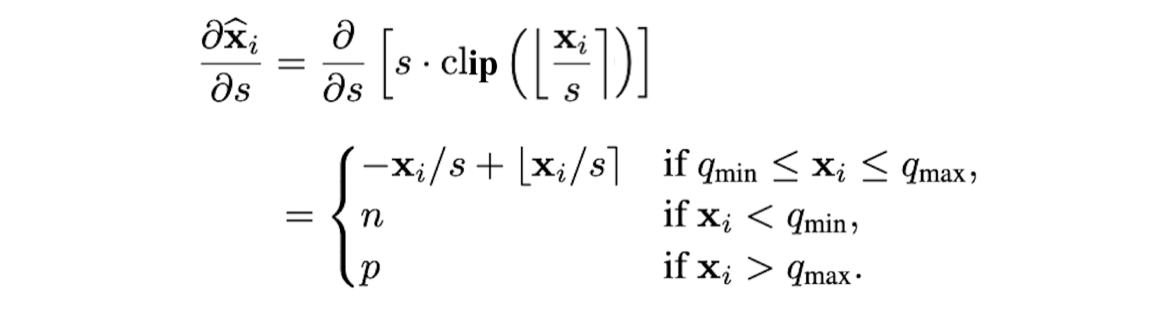
gradient w.r.t $z$
위에서 zero-point를 정수로 한정했지만, zero-point를 learnable하게 만들기 위해 real number로 바꾸고, rounding operator를 적용하여 quantization function을 작성하면 다음과 같다.

zero-point의 rounding operator에 대해 STE를 적용하면 다음과 같다.

4.2 BN folding

BN의 scaling과 shift parameter를 linear layer의 weight와 bias로 흡수하여, inference 시 효율성을 높임을 살펴봤다. QAT에서도 Inference 시점의 동작을 정확히 simulation하기 위해, BN Folding을 고려해야 한다.

일부 QAT 문헌에서는 BN Folding 효과를 무시한다. 이는 per-channel quantization을 사용할 때는 괜찮지만, per-tensor quantization을 사용할 때는 다음과 같은 문제가 발생할 수 있다.

• 문제 1: BN layer가 per-channel rescaling을 적용
  $\\$
  QAT 동안 BN layer가 unfolded 상태로 유지되면, BN layer는 각 채널에 대해 별도의 scaling과 shift를 적용한다.
  $\\$
  영향: 이로 인해 per-tensor quantization과의 불일치가 발생한다.
  per-tensor quantization은 전체 tensor에 대해 단일 scale factor를 사용하지만, BN layer는 각 channel마다 다른 scale factor를 적용한다.
  $\\$
  결론: BN layer가 per-channel rescaling을 적용하려면 처음부터 per-channel quantization을 사용하는 것이 더 적합하다.

• 문제 2: BN을 weight tensor에 접목하여 deployment
  $\\$
  BN layer가 unfolded 상태로 QAT가 수행된 후,
  inference 시에는 BN 연산을 제거하고, 해당 parameter들을 weight tensor에 접목하여 배포한다.
  $\\$
  영향: 학습 동안 네트워크는 BN layer가 unfolded 상태에서 per-tensor quantization noise에 적응한다.
  하지만, BN 연산을 weight tensor에 접목하는 과정에서 network는 새로운 quantization noise를 경험하게 된다.
  $\\$
  결론: QAT 동안 BN folding을 고려하지 않으면,모델이 학습 시 경험한 quantization noise와 deployment 시 적용된 quantization noise가 달라지게 되어, 성능 drop으로 이어질 수 있다.

QAT에서 BN-folding을 적용하는 간단하지만 효과적인 방법은, 수식 (11)과 (12)에서 보았던것과 같이, BN scale과 shift를 linear layer의 weight와 bias로 statically fold 하는 방법이다.

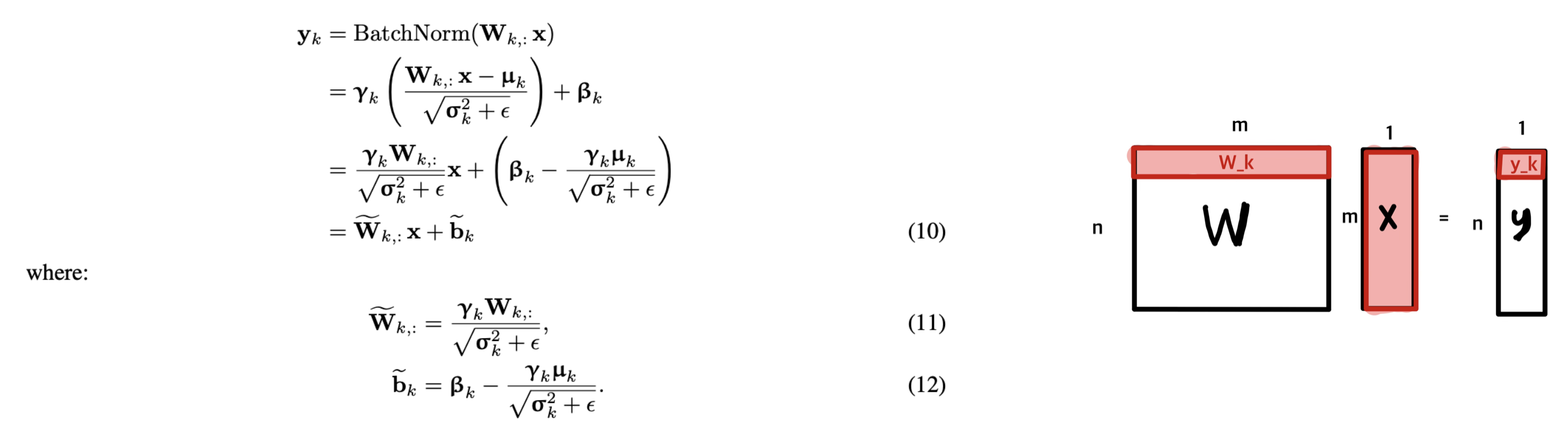
이는 network에서 BN 연산을 모두 제거하고 weight를 re-parametirzation하는 것과 같다.
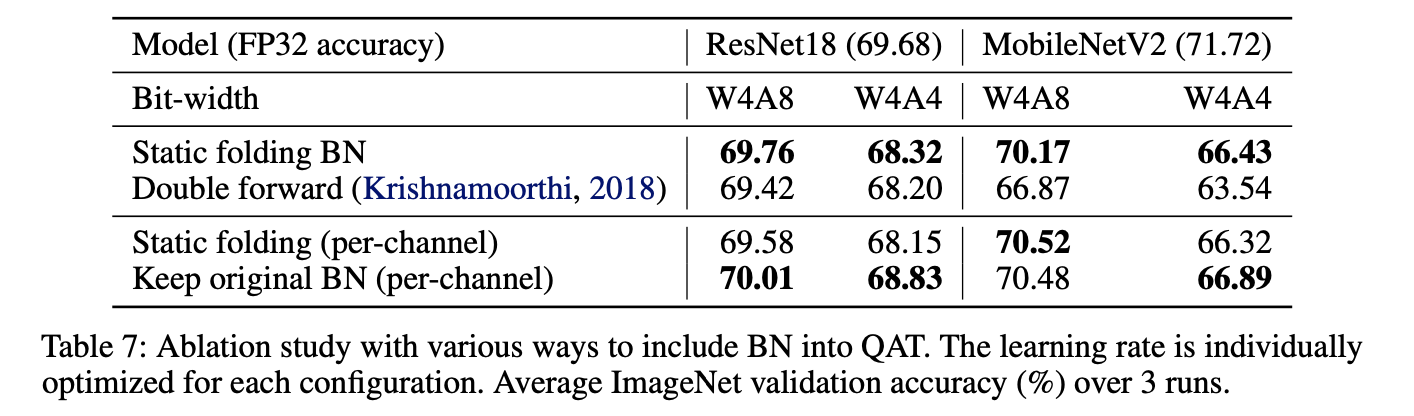
수렴한 pre-trained 모델에서 시작한다면, static folding은 매우 효율적이다.(Table 7)

Per-channel quantization

hardware만 지원된다면 weight의 per-channel quantization은 accuracy를 향상할 수 있음을 밝혔었다.

BN scale parameter를 per-channel scale-factor로 흡수할 수 있다.

weight의 per-channel quantization이 $\hat{\bold{W}_{k,:}} = q(\bold{W}_{k,:};s_{\bold{W},k}) = s_{\bold{W},k}\bold{W}^{int}_{k,:}$ 일 때,
BN을 linear layer의 output에 적용하는 수식은 다음과 같다.

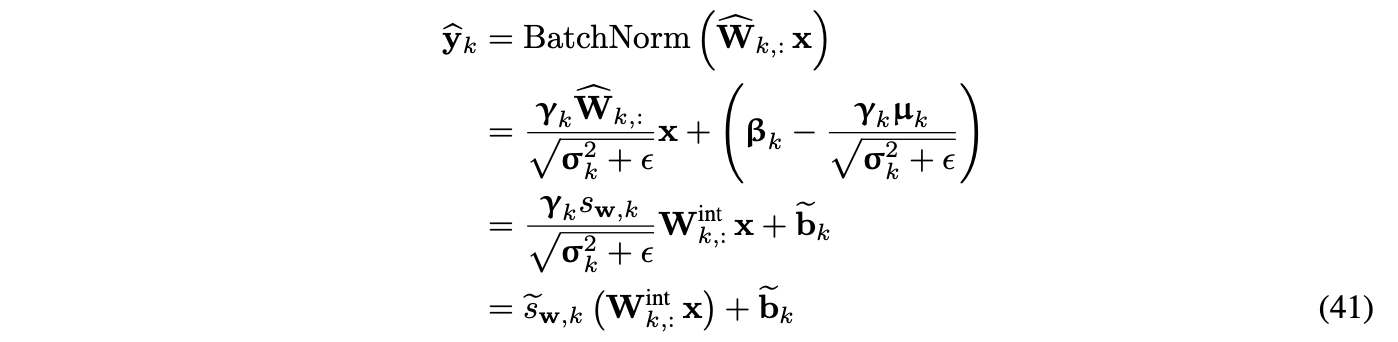
Table 7의 마지막 두 행에서 볼 수 있듯, static folding에 비해 per-channel quantization에 더 좋은 성능을 보임을 알 수 있다.

4.3 Initialization for QAT

pre-trained된 FP32 모델에서 시작하는 것이 보편적이고 유리하지만,
quantization initialization가 최종 QAT에 미치는 영향은 연구가 적기에,
QAT 이전에 pre-trained된 FP32 모델에 몇 가지 PTQ 기술을 initial step으로 사용하는 것의 영향을 살펴보았다.

결론을 먼저 말하면, PTQ 기술을 적용하는 것이 초기 단계에서는 이점이 있을 수 있지만, 장기적인 QAT 결과에는 대부분의 경우 큰 영향을 미치지 않았다.

Effect of range estimation

weight와 activation의 initial range setting의 영향을 평가하기 위한 실험을 진행했다.

• weight quantization
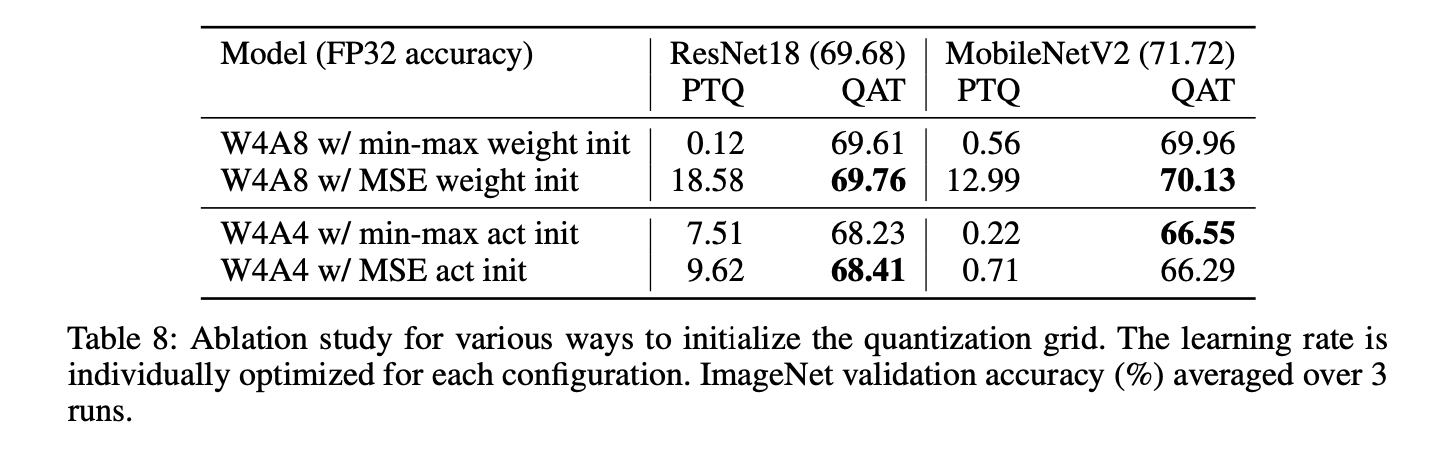
  weight를 4 bit로, activation을 8 bit로 quantize한 다음,
  weight의 quantization range 설정을 위한 min-max init과 MSE based init 방법을 비교했다.
  $\\$
  결과: MSE init이 초기에 더 높은 accuracy를 보이지만, 20 epoch training 후 차이가 줄어들었다.
  

• activation quantization
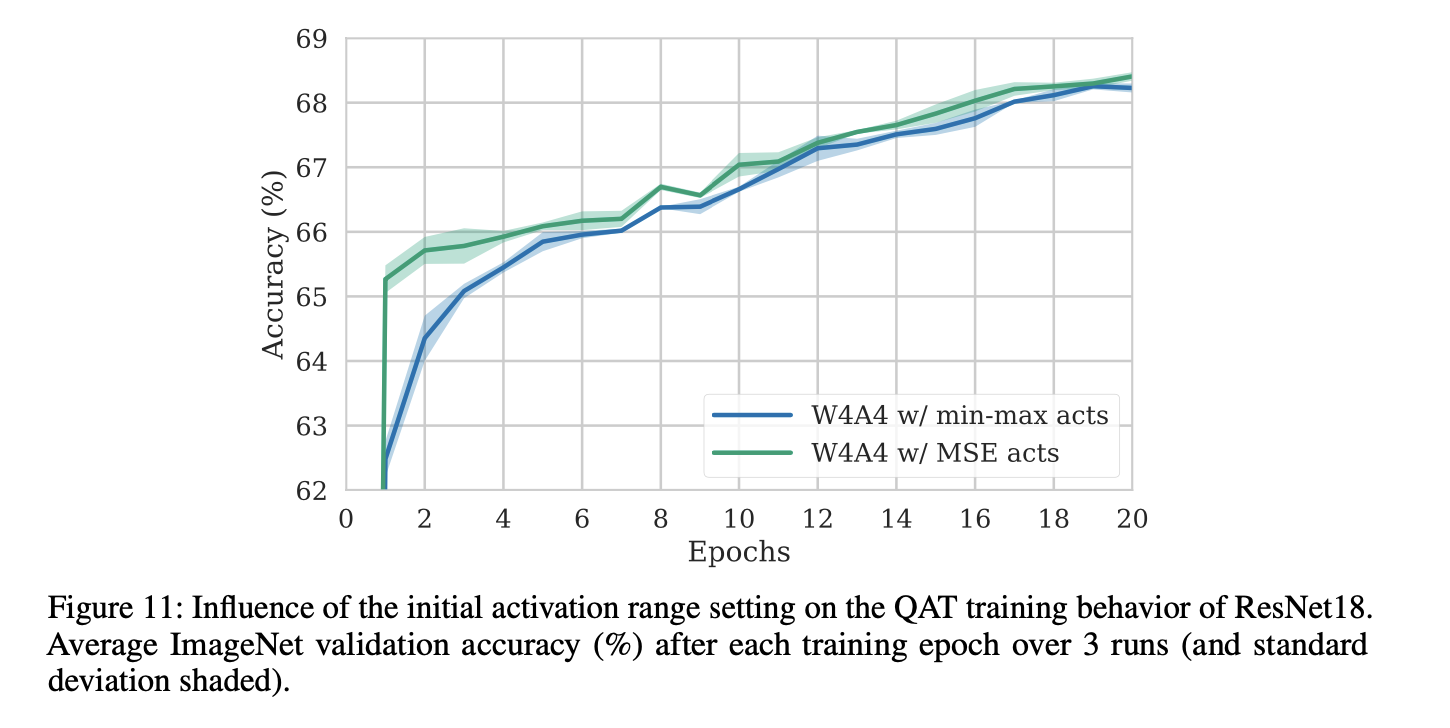
  weight를 4 bit, activation을 4 bit로 quantize한 다음,
  activation의 quantization range 설정을 위한 min-max init과 MSE based init 방법을 비교했다.
  $\\$
  결과: weight quantization 실험과 유사하게, MSE init이 초기에 더 높은 accuracy를 보이지만, 20 epoch training 후 차이가 줄어들었다.
  

Effect of CLE

PTQ의 개선 기법들인 CLE와 bias correction가 QAT에 미치는 영향을 실험했다.

ResNet18의 경우, QAT 성능에 큰 영향이 없었다.

MobileNetV2의 경우, CLE는 필수적이었다. 이는 per-tensor quantization으로 인한 성능 drop 때문일 가능성이 높다.

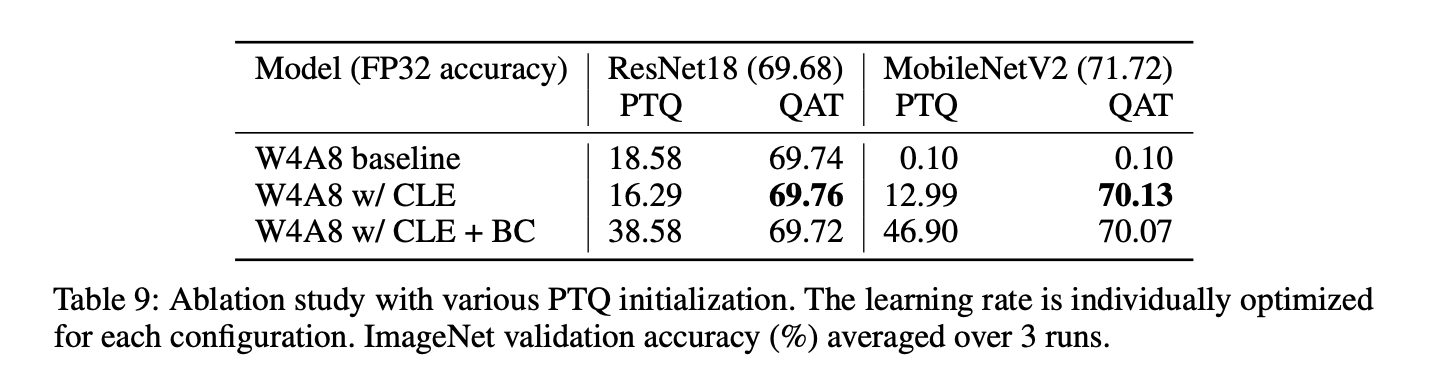
결론적으로,Q PTQ로 인해 성능 drop이 너무 크다면 CLE와 같은 PTQ 향상 기법을 사용해 QAT 이전에 init 하는게 필요하다.
하지만 거의 모든 다른 경우에선, PTQ init은 최종적인 QAT 성능에 크게 영향을 미치지 않았다.

4.4 Standard QAT pipeline

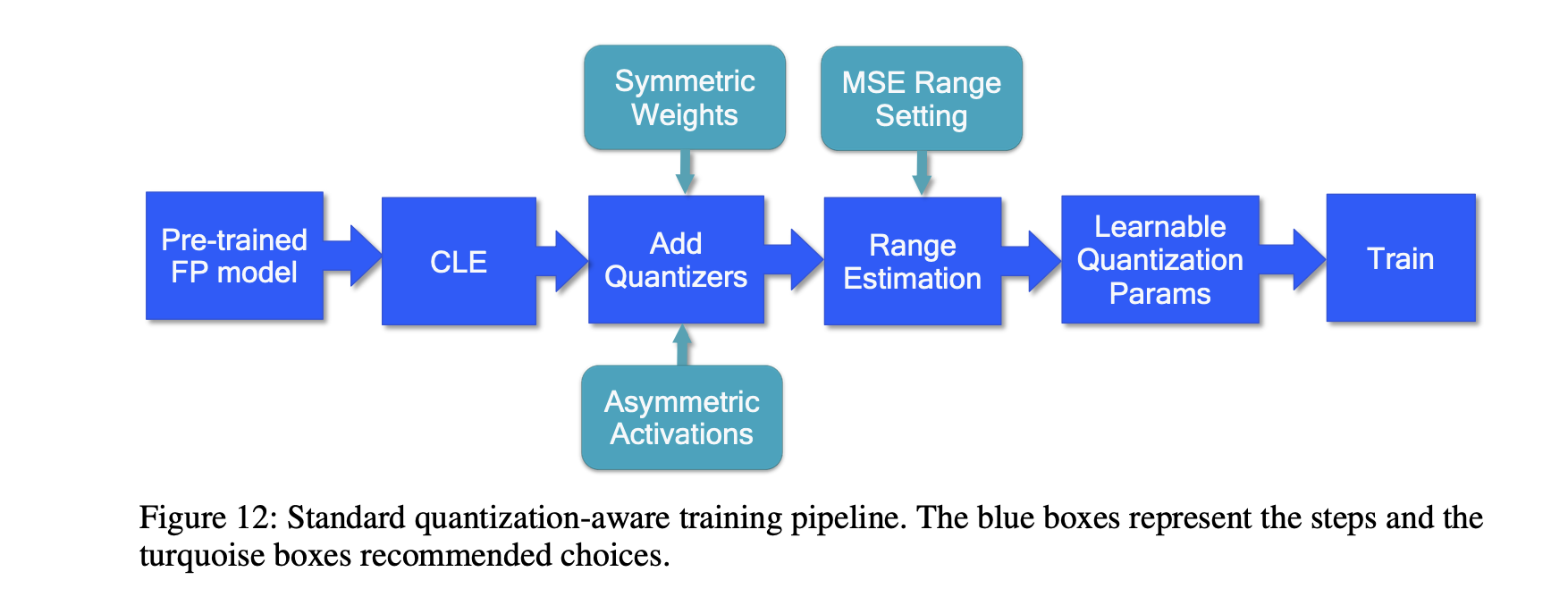
CLE(Cross-layer qualization)
PTQ와 유사하게, FP 모델에 CLE를 적용한다.
특히, MobileNet 구조처럼 imbalanced weight distribution으로 인해 문제가 되는 모델에 중요하다.
다른 network 또는 per-channel quantization의 경우 이 단계는 optional하다.

Add quantizers
특정 targe HW에 따라 quantizer를 무엇으로 하느냐는 달라지지만,
보통 weight는 symmetric quantizer, activation은 asymmetric quantizer를 추천한다.
HW/SW stack이 지원된다면, weight는 per-channel quantization을 사용하는 것이 좋다.
이 단계에서, BN simulation이 정확한지 신경써야 한다.

Range estimation
training 이전에 모든 quantization parameter를 initialize 해야 한다.
더 나은 initialization은 더 빠른 training을 가능케하고, 최종 accuracy를 (조금이나마) 높인다.
통상적으론, layer-wise MSE based criteria를 사용해 모든 quantization parameter를 setting하는 것을 추천한다.
per-channel을 사용하는 경우엔 min-max setting을 사용하는 것이 좋은 경우도 때때로 있따.

Learnable Quantization Parameters
quantizer parameter를 learnable하게 만드는 것을 추천한다.
low-bit quantization을 시도할 경우, quantization parameter를 leraning하는 것이
매 epoch마다 quantization parameter를 update하는 것보다 성능에 더 효과적이다.

learnable quantizer의 경우, optimizer를 세팅할 때 주의를 기울여야 한다.
SGD-type의 optimizer를 사용할 경우, quantization parameter들의 learning rate는 다른 network parameter들에 비해 줄여야 한다.
adaptive leraning rate를 사용하는 optimizer들 (Adam 또는 RMSProp)의 경우 별도의 learning rate 조절은 필요하지 않다.

4.5 Experiments

optimizer: Adam
각 quantization config에 best learning rate을 적용한 결과이며, 추가적인 hyper-parameter tuning은 진행하지 않음.

• Semantic Segmentation
  model: DeepLabV3 (with MobileNetV2 backbone)
  dataset: Pascal VOC
  epoch: 80

• Object Detection
  model: EfficientDet
  dataset: COCO 2017
  epoch: 20

• Image Classification
  model: ResNet18, ResNet50, MobileNetV2, InceptionV3, EfficientNet lite
  dataset: ImageNet
  epoch: 20

• Natural Language Understanding
  model: BERT-base
  dataset: GLUE benchmark
  epoch: 3~12 epochs (task와 quantization graularity에 따라)

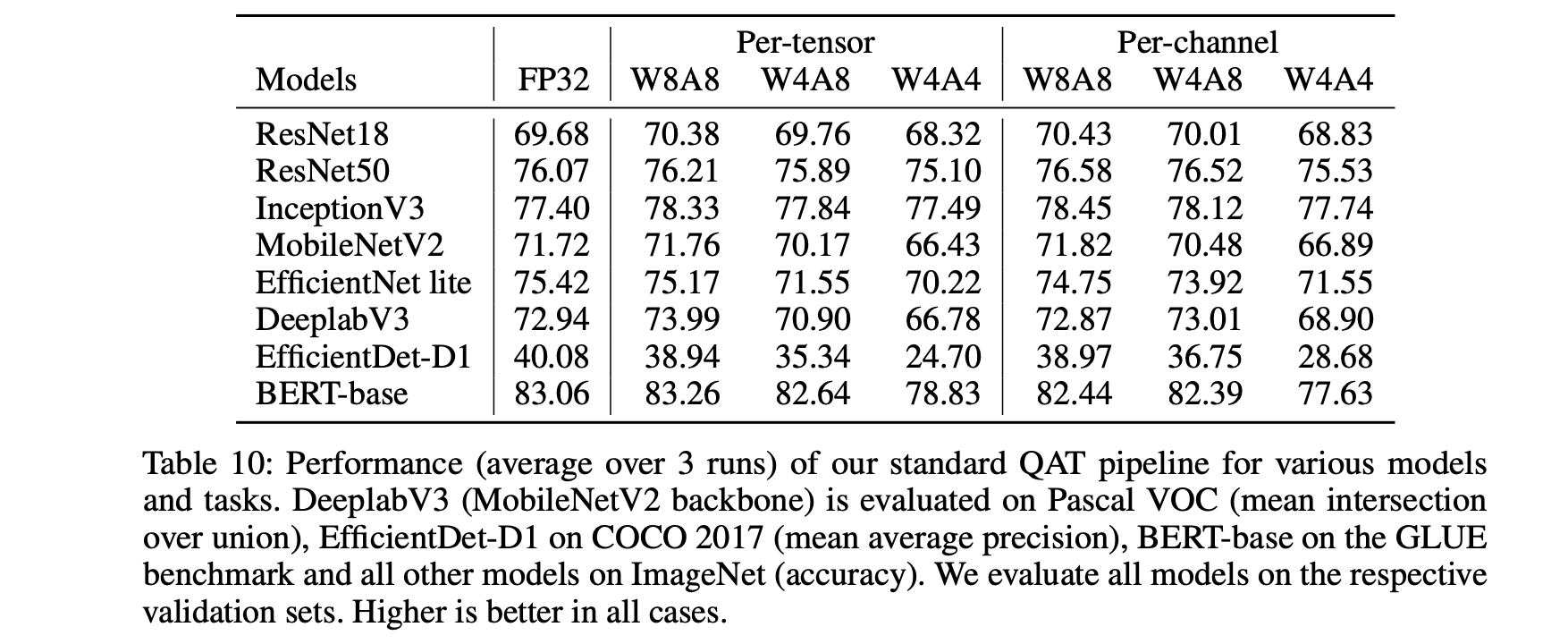
실험 결과

networks w/o depth-wise separable convolutions(1~3행)
W8A8, W4A8: FP 모델과 유사하거나 오히려 더 잘 나오는 경우도 있는데,
아마 quantization noise를 training하는 regularizing 효과 또는 QAT 과정에서의 추가적인 fine-tuning 때문일 수 있다.

W4A4: 약간의 drop이 있지만, FP accruacy의 1% 이내.

networks w/ depth-wise separable convolutions(4~7행)

3.6의 PTQ 실험 결과에서 알 수 있듯 더 challenging함.

weight의 8 bit quantization은 거의 accuracy drop이 없거나 적으나,
weight의 4 bit quantization의 경우 accuracy drop이 크다.
(EfficientNet lite를 per-tensor quantization한 경우 4% drop)

per-channel quantization은 성능을 크게 향상할 수 있음을 보였다.

W4A4는 per-channel quantization을 적용해도 몇몇의 network에선 여전히 challenging하다.
EfficientDet-D1이 다른 network에 비해 이 quantization이 어려웠다.

BERT-base
QAT + range learning을 통해 high dynamic ragne를 잘 극복했고, PTQ와 달리 모든 activation을 8 bit로 줄였다.

W4A8: 기존 GLUE score 1% drop 이내
이는 low bit weight quantization이 transformer 모델들에게도 문제가 아님을 의미한다.

W4A4: 이건 좀 어렵더라.