
GPTQ: ACCURATE POST-TRAINING QUANTIZATION FOR GENERATIVE PRE-TRAINED TRANSFORMERS
GPTQ ALGORITHM
Step 1: Arbitrary Order Insight
OBQ의 경우, 현재 시점에서 가장 적은 quantization error를 유발하는 weight를 선택하여 quantization하는 greedy order를 사용한다.
그런데, OBQ의 greedy하게 Q하는 전략은 임의의(arbitrary) 순서로 Q하는 것과 큰 차이가 없음을 발견했다. (특히 large, heavily-parametrized layer의 경우)
그 이유는, OBQ의 greedy 방법은 초기에 Q error가 큰 weight 수를 줄일 수 있지만, 후반부에 이르면, 보상을 위해 조정할 수 있는 weight가 거의 남아 있지 않게 되어, 후반부에 Q되는 weight들은 더 큰 error를 발생시킬 수 있다.
결과적으로, 초기의 이점(개별 error가 큰 weight 수의 감소)이 후반부의 불리함 (더 큰 error를 가진 weight들)에 의해 상쇄된다.
어떤 fixed order도 꽤 잘 동작한다는 insight는 특히 large model에서 흥미로운 가능성을 갖는다.
"
기존 OBQ 방법은 의 각 row들을 independent하게, quantization error를 최소화하는 weight를 선택해 quantization한다.
반면, GPTQ에선 모든 row들을 동일한 order로 quantization 한다.
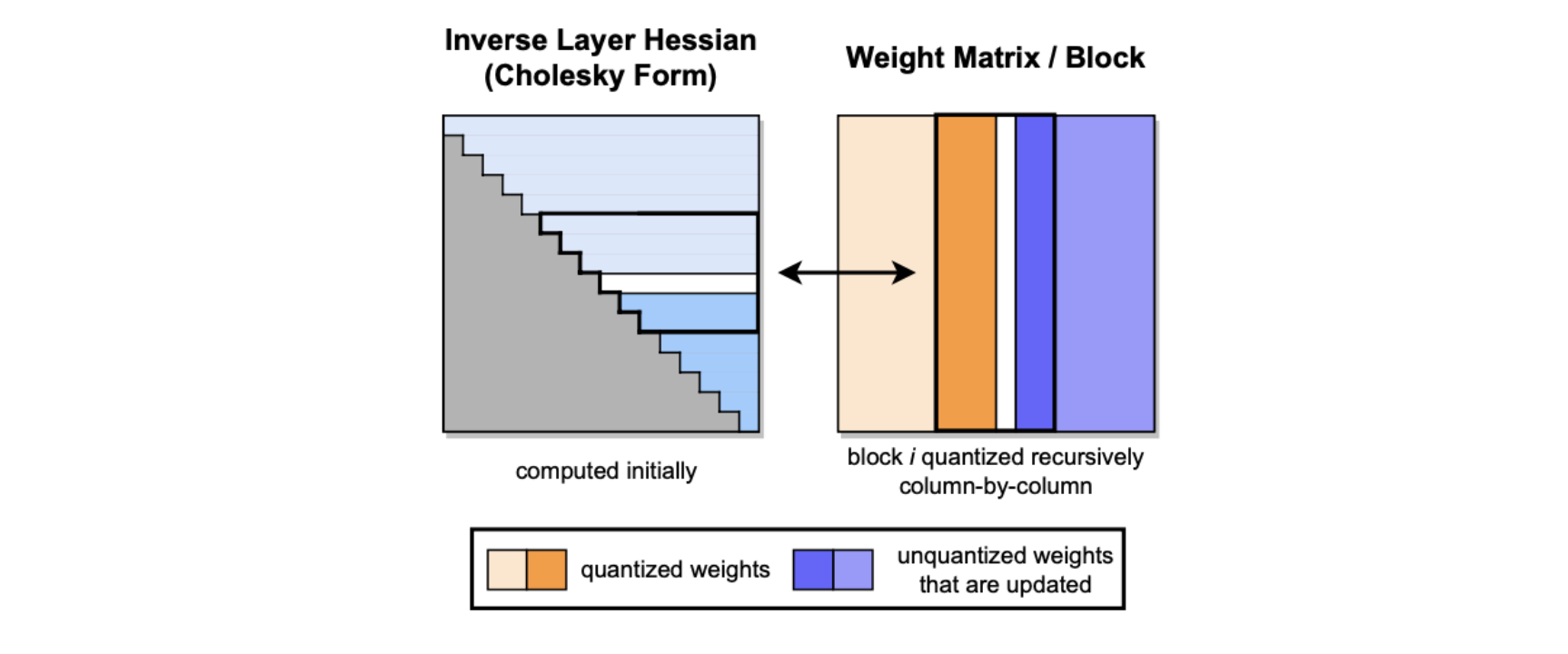
"
결과적으로, unquantized weights 와 가 모든 row에서 동일하다.
따라서, 각 column을 update할 때마다, 번만 update 하면 된다.
(기존 OBQ에선 각 weight를 quantiation 할 때마다,번 update 필요)
이를 통해, 전체적인 runtime을 에서
으로 줄일 수 있다.(by factor of )
update에 소요.
large model에 대해서, 이 효과는 수백~수천 배 커진다.
하지만, 이 알고리즘이 실제로 very large model에 실전에 적용해되기 위해선, 2가지 주요한 문제를 해결해야 한다.
Step 2: Lazy Batch-Updates
핵심: "GPTQ는 여러 column들을 한 번에 batch로 처리하는 batch-update 방식을 도입했다."
문제
Step 1에서 제안한 방식을 그대로 구현하는 것은 상대적으로 낮은 compute-to-memory-access ratio를 갖기에 빠르지 않다.
착안
번째 column에 대한 최종 rounding decision은 오직 이 column에 대해 수행된 updates에만 영향을 받으므로, 이 시점에서 이후 column들에 대한 업데이트는 무관하다. 이를 통해 updates를 'lazily batch' updates 할 수 있게 되어, GPU 활용도를 크게 개선할 수 있다.
해결 방안
GPTQ는 한 번에 의 column에 알고리즘을 적용하며, updates를 해당 column들과 의 해당 블록으로 제한한다. (Figure 2)

Block이 완전히 처리된 후에, 아래에 제시된 Euqation (2)와 (3)의 multi-weight version을 사용해 전체 와 행렬에 대해 global updates를 수행한다.
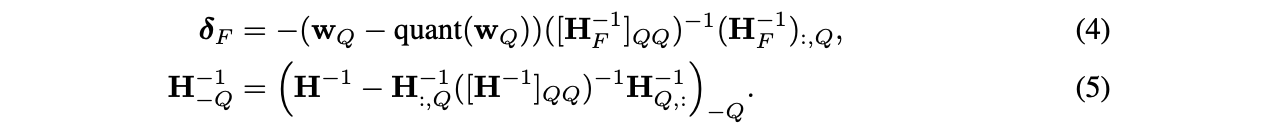
: set of indices, : inverse matrix with the corresponding rows and columns removed
비록 이 전략이 이론적인 계산량을 줄이지는 않지만, 메모리 처리량 병목 현상(memory-throughput bottleneck)을 효과적으로 해결한다. 이는 실제로 매우 큰 모델에서 10배 정도의 속도 향상을 제공하며, 따라서 알고리즘의 핵심 구성 요소가 된다.
Step 3: Cholesky Reformulation
핵심: "GPTQ는 Cholesky 분해를 도입하여 수치적(numerical) 안정성 문제를 해결하고, 대규모 모델(large model)에 적용 가능한 알고리즘을 개발했다."
문제
-
수치적 부정확성(numerical inaccuracies)이 large 모델에서 주요 문제가 된다.
(특히, Step 2의 block updates를 함께 적용하는 경우 더욱더) -
구체적으로, 행렬이 indefinite 해질 수 있고, 이로 인해 remaining weights들이 잘못된 방향으로 aggressive하게 update 되어, 해당 layer의 arbitrarily-bad quantization을 초래한다.
-
실전에서, model size가 커질수록 이 문제가 발생할 가능성이 증가한다. 수십억 개 이상의 parameter를 가진 model에선 몇몇 layer에서 이 문제가 거의 확실히 발생함을 관찰했다.
-
주요 issue는 반복적인 Equation (5)의 적용, 즉 반복적인 batch Hessian inverse update로 인한 것으로 보이며, 특히 matrix inversion을 통해 numerical error가 축적되는 것으로 보인다.
-
더 작은 모델의 경우, dampening을 적용하는 것, 즉 H의 대각 요소에 작은 상수 λ (우리는 항상 평균 대각 값의 1%를 선택합니다)를 추가하는 것이 수치적 문제를 피하기에 충분해 보인다.
그러나 더 큰 모델들은 더 robust하고 일반적인 접근 방식을 필요로 한다.
착안
- 번째 가중치를 양자화할 때, 행렬(아직 quantized 되지 않은 weights set)의 번째 행에서 번째 요소(diagonal)부터 마지막 요소까지만 필요로 한다. 이는 아직 quantized 되지 않은 weight들과의 관계만을 고려하기 때문이다
해결 방안
-
Cholesky decomposition(분해) 도입
- 행렬을 Cholesky 분해하여 수치적으로 더 안정적인 형태로 변환한다.
- 에서 q번째 row와 column을 제거하는 Equation (3)을 사용하는 것과 본질적으로 같다. 단지, Cholesky 분해의 경우 의 제곱근으로 나눠 정규화해주는 것만 추가된다.
-
에서 필요한 q번째 행의 대각선 이후 요소들만 미리 계산 (선택적 계산)
-
최신 Cholesky kernel을 사용하여 계산 속도 향상
-
약간의 dampening (의 diagonal 요소에 작은 상수 추가)을 적용하여 추가적인 수치 안정성(numerical stability) 확보
이 접근 방식은 메모리 사용량을 크게 증가시키지 않으면서도 수치적 안정성을 확보하며, 대규모 모델에서도 robust하게 작동한다.
Full Algorithm

Experimental Validation
Overview
-
smaller model들에 대해 GPTQ의 accuracy를 다른 (accurate-but-expensive) quantization 방법들과 비교하여 검증한다.
-
large model들에 대한 GPTQ의 runtime scaling을 실험한다.
-
BLOOM과 OPT model family 전체에 대한 3-bit 및 4-bit quantization 결과를 제시하며, 이는 challenging한 language generation task에서의 perplexity를 통해 평가된다.
-
weight들의 작은 block으로 granularity를 줄일 때 2-bit quantization에도 stable함을 보여준다.
-
perplexity 분석을 보완하기 위해, 결과로 얻어진 quantized model들을 일련의 standard zero-shot task에서도 평가한다.
-
공개적으로 사용 가능한 가장 큰(그리고 흥미로운) 두 model인 Bloom-176B와 OPT-175B에 초점을 맞추어 여러 task에 대해 상세한 evaluation을 수행한다. 이 model들에 대해, inference에 필요한 GPU 수를 줄이고 generative task에 대한 end-to-end speedup과 같은 practical improvement들을 제시한다.
Setup
-
GPTQ를 PyTorch (Paszke et al., 2019)로 구현하였고, BLOOM (Laurençon et al., 2022)과 OPT (Zhang et al., 2022) model family의 HuggingFace integration을 사용했다.
-
모든 model (1750억 parameter variant 포함)을 80GB memory를 가진 단일 NVIDIA A100 GPU를 사용하여 quantize했다.
-
GPTQ calibration data는 C4 dataset (Raffel et al., 2020)에서 무작위로 선택한 128개의 2048 token segment로 구성되었다. 이는 무작위로 크롤링된 웹사이트에서 발췌한 것으로, 일반적인 text data를 대표한다. 이는 GPTQ가 task-specific data를 전혀 보지 않았음을 의미하며, 따라서 우리의 결과가 실제로 "zero-shot"임을 강조한다.
-
LLM.int8() (Dettmers, 2022)와 유사하게 min-max grid에서 standard uniform per-row asymmetric quantization을 수행한다.
추가적인 evaluation 세부사항은 Appendix A.2.1에서 찾을 수 있다. -
전체 compression 과정이 full precision model 실행에 필요한 것보다 훨씬 적은 GPU memory로 수행될 수 있도록 하기 위해 몇 가지 주의가 필요하다. 구체적으로, 우리는 항상 6개의 layer로 구성된 하나의 Transformer block을 한 번에 GPU memory에 load하고, 그 다음 layer-Hessian을 누적하고 quantization을 수행한다. 마지막으로, 현재 block input을 fully quantized block을 통해 다시 보내어 다음 block의 quantization을 위한 새로운 input을 생성한다. 따라서 quantization 과정은 full precision model의 layer input이 아니라 이미 부분적으로 quantize된 model의 실제 layer input에 대해 작동한다. 우리는 이 방법이 무시할 만한 추가 비용으로 눈에 띄는 개선을 가져온다는 것을 발견했다.
Baselines
-
primary baseline인 RTN은 정확히 동일한 asymmetric per-row grid에서 모든 weight들을 가장 가까운 quantized value로 rounding하는 것으로 구성된다.
-
GPTQ에서 사용되는 것과 정확히 동일하다.
-
이는 LLM.int8() 의 SOTA weight quantization과 정확히 일치한다.
-
이는 현재 매우 큰 language model의 quantization에 관한 모든 연구(LLM.int8(), ZeroQuant, nuQmm)에서 사용되는 method이다.
-
단순히 direct rounding을 수행하기 때문에 수십억 개의 parameter를 가진 network에 대해서도 runtime이 잘 scaling된다.
-
AdaRound(Nagel et al., 2020)나 BRECQ(Li et al., 2021)와 같은 더 accurate한 method들은 현재 수십억 개의 parameter를 가진 model들에 대해서는 너무 느리다. GPTQ 연구의 main focus가 이 지점이다.
-
GPTQ는 small model에 대해서는 이러한 method들과 competitive하면서도 OPT-175B와 같은 huge model로도 scaling 가능함을 보여준다.
-
Quantizing Smaller Models
-
ablation study 1: ResNet18과 ResNet50에 대해 GPTQ의 성능을 state-of-the-art post-training quantization (PTQ) method들과 비교.
- 이는 standard PTQ benchmark로, LLM.int8()와 동일한 setup에서 수행.
-
실험 결과 (Table 1)
- GPTQ는 4-bit에서 동등한 성능을 보이고, 3-bit에서는 가장 accurate한 method들보다 약간 낮은 성능
- 기존 PTQ method 중 가장 빠른 AdaQuant보다 성능 향상.
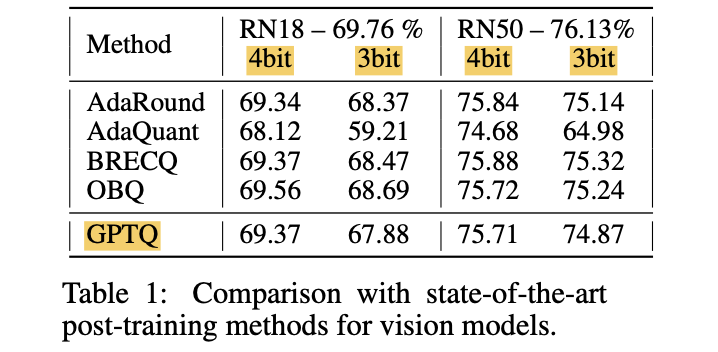
-
ablation study 2: 두 개의 smaller language model인 BERT-base (Devlin et al., 2019)와 OPT-125M에 대해 full greedy OBQ method와 비교
-
실험 결과 (Appendix Table 8)
- 4-bit에서는 두 method가 유사한 성능
- 3-bit에서는 놀랍게도 GPTQ가 약간 더 나은 성능.
(우리는 이 이유에 대해 OBQ가 사용하는 일부 additional heuristic (예: early outlier rounding)이 non-vision model에 대한 optimal performance를 위해 careful adjustment가 필요할 수 있기 때문이라고 추측)

-
전반적으로, GPTQ는 smaller model에 대해 state-of-the-art post-training method들과 competitive한 성능을 보이면서도, ≈ 1시간이 아닌 < 1분만 소요된다. 이를 통해 much larger model로의 scaling이 가능해진다.
Runtime
- GPTQ를 사용한 full model quantization time을 (단일 NVIDIA A100 GPU에서) 측정.
- 실험 결과(Table 2)
- GPTQ는 1-3 billion parameter model을 수 분 내에, 175B model을 몇 시간 내에 quantize.
- 참고로, straight-through 기반 method인 ZeroQuant-LKD (Yao et al., 2022)는 1.3B model에 대해 (동일한 hardware에서) 3시간의 runtime을 보고하는데, 이를 linear extrapolation하면 175B model에 대해서는 수백 시간(몇 주)이 소요될 것이다.
- Adaptive rounding 기반 method들은 일반적으로 훨씬 더 많은 SGD step을 사용하므로 더욱 expensive할 것이다 ( AdaRound(Nagel et al., 2020), BRECQ(Li et al., 2021) )

Quantizing Large Models
-
arge-scale study는 전체 OPT와 BLOOM model family를 3-bit와 4-bit로 compress하는 것으로 시작.
-
그 후 이 model들을 WikiText2 (Merity et al., 2016) (Figure 1, Table 3,4), Penn Treebank (PTB) (Marcus et al., 1994), C4 (Raffel et al., 2020) (둘 다 Appendix A.3에 있음)를 포함한 여러 language task에서 evaluate한다.
-
이러한 perplexity-based task에 focus를 두는데, 이는 model quantization에 particularly sensitive한 것으로 알려져 있기 때문이다 (ZeroQuant, (Yao et al., 2022))
-
실험 결과(Table 3)
- OPT model에서 GPTQ는 RTN을 significant margin으로 명확히 outperform
- 4-bit quantization 시 perplexity GPTQ는 175B 0.03 감소, RTN은 2.2 감소(10배 작은 full-precision 13B model보다 더 나쁜 성능)
- 3-bit에서는 RTN이 완전히 collapse되는 반면, GPTQ는 여전히 reasonable perplexity를 유지
- OPT model에서 GPTQ는 RTN을 significant margin으로 명확히 outperform
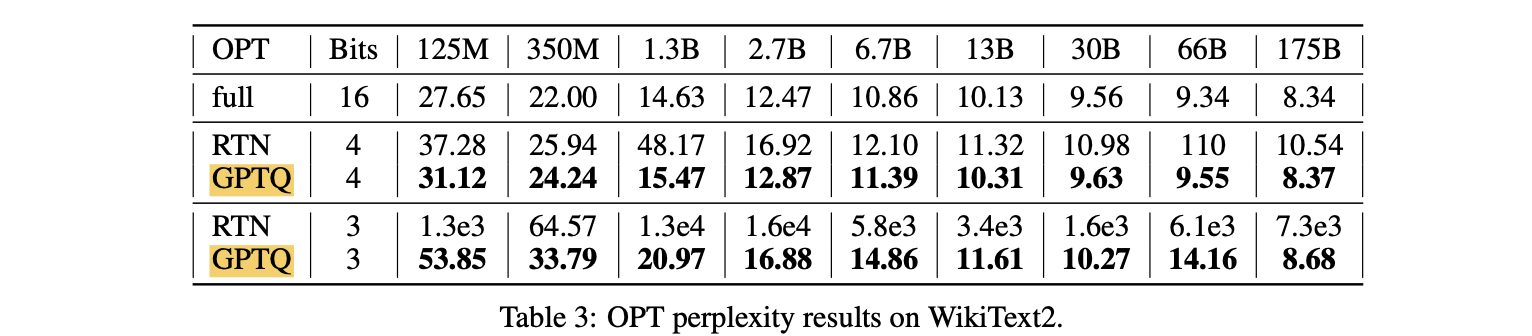
-
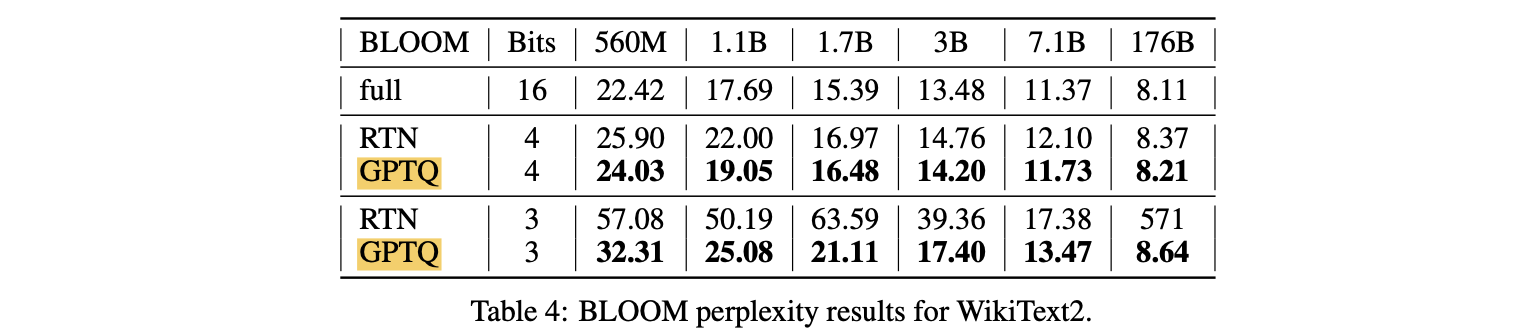
실험 결과(Table 4)
- BLOOM 실험 결과도 유사한 pattern을 보임.
- 하지만 method 간 gap이 대체로 더 작은데, 이는 이 model family가 quantize하기 더 쉬울 수 있음을 시사함.
-
실험 결과(Figure 1)
- 한 가지 interesting trend는 larger model이 일반적으로 (OPT-66B 제외) quantize하기 더 쉬워 보인다는 것. 이는 practical application에 좋은 news인데, 이러한 case가 compression이 가장 필요한 경우이기 때문이다.
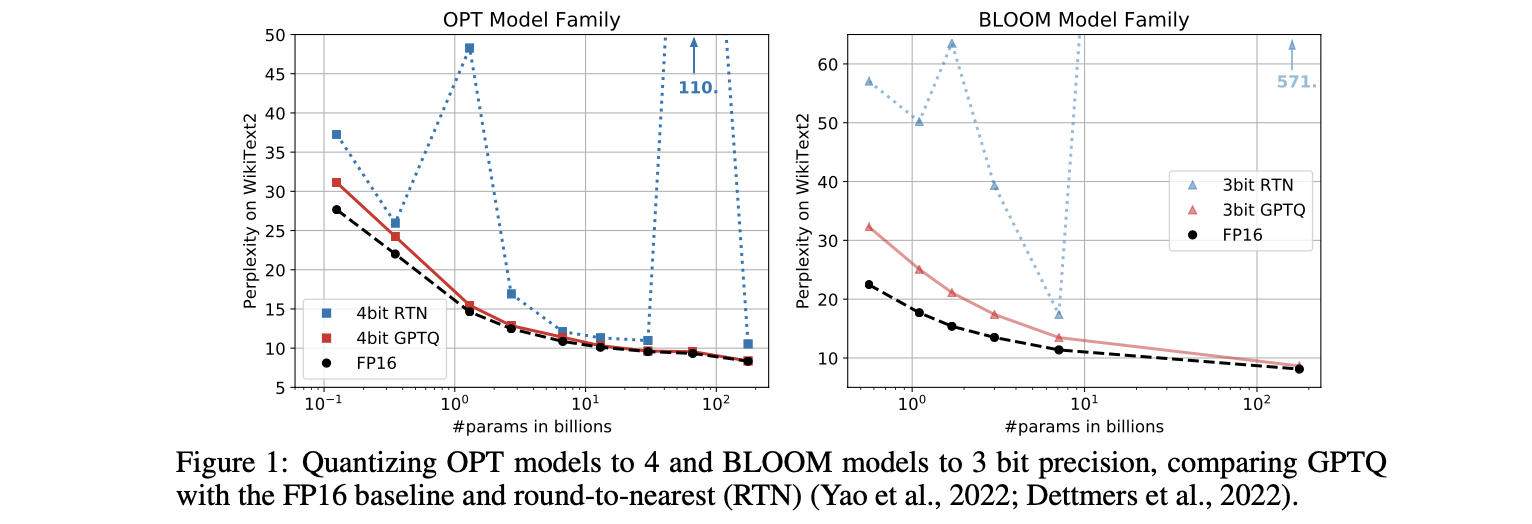
- 한 가지 interesting trend는 larger model이 일반적으로 (OPT-66B 제외) quantize하기 더 쉬워 보인다는 것. 이는 practical application에 좋은 news인데, 이러한 case가 compression이 가장 필요한 경우이기 때문이다.
175B Parameter Model
- 공개적으로 사용 가능한 가장 큰 dense model인 BLOOM-176B와 OPT-175B를 quantize
- text dataset: Wikitext-2, PTB, C4
- GPTQ의 accuracy는 finer-granularity grouping (nuQmm (Park et al., 2022))을 통해 further improve될 수 있음.
- 이는 group parameter가 각 layer의 quantization process 동안 결정 될 수 있고, 항상 가장 current한 updated weight를 사용하기 때문이다.
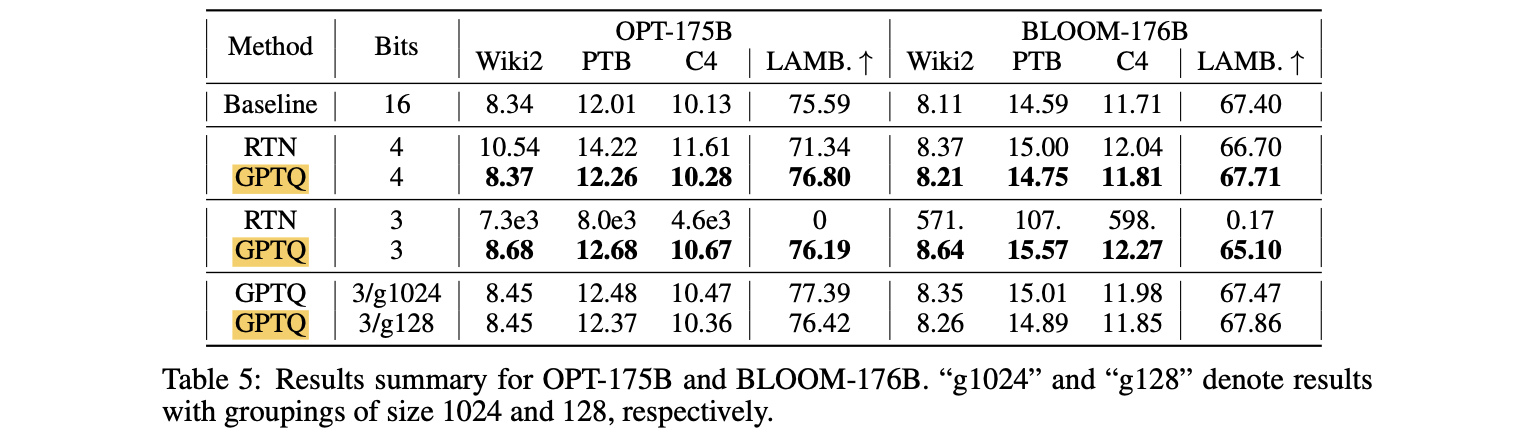
- 실험 결과(Table 5)
- GPTQ는 4-bit에서 full-precision version보다 perplexity가 ≤ 0.25 정도만 낮음.
- 3-bit에서는 RTN이 collapse되는 반면, GPTQ는 대부분 good performance를 유지.
- group-size 1024 (≈ 0.02 extra bit)는 평균적으로 perplexity를 약 0.2 정도 improve
- group-size 128 (≈ 0.15 extra bit)은 추가로 0.1 정도 improve.
Practical Speedups
-
OPT-175B model에 practical appication study.
-
GPU memory cost
- 3-bit로 quantize된 이 model은 embedding과 output layer (full FP16 precision으로 유지됨)를 포함하여 약 63GB의 memory를 차지
- 추가로, generation task를 위한 common optimization인 모든 layer의 key와 value의 complete history를 저장하는 데 최대 2048 token에 대해 약 9GB가 더 필요.
- 따라서, 우리는 실제로 entire quantized model을 단일 80GB A100 GPU에 fit할 수 있으며, 이는 inference 중 필요에 따라 layer를 dynamically dequantizing하여 execute할 수 있다 (4-bit를 사용하면 model이 fully fit하지 않음)
- 참고로, standard FP16 execution은 5x80GB GPU가 필요하고, SOTA 8-bit LLM.int8() quantizer (Dettmers et al., 2022)는 3x80GB GPU가 필요하다.
-
Latency
-
LLM.int8()은 FP16 baseline과 동일한 runtime을 가짐.
-
문제
- Language generation에서 model은 한 번에 하나의 token을 process하고 output하는데, OPT-175B의 경우 token당 쉽게 수백 millisecond가 걸릴 수 있다.
- User가 생성된 결과를 받는 속도를 높이는 것은 challenging한데, compute가 matrix-vector product에 의해 dominate되기 때문이다. Matrix-matrix product와 달리, 이들은 주로 memory bandwidth에 의해 limited된다.
-
해결
- 필요할 때 weight를 dynamically dequantizing하여 matrix vector product를 수행하는 quantized-matrix full-precision-vector product kernel을 develop하여 address한다.
- 가장 주목할 만한 점은, 이것이 activation quantization을 전혀 필요로 하지 않는다는 것이다.
- Dequantization이 extra compute를 consume하지만, kernel이 훨씬 적은 memory에 access해야 하므로 significant speedup을 lead한다.
- speedup의 거의 모든 부분이 우리의 kernel로 인한 것임을 강조한다. 왜냐하면 communication cost가 우리의 standard HuggingFace-accelerate-like setting에서 negligible하기 때문이다 (Appendix A.2.2).
-
실험 결과 (Table 6)
- 단일 A100에서 실행되는 GPTQ를 통해 얻은 3-bit OPT-175B model이 token당 평균 시간 측면에서 FP16 version (5 GPU에서 실행)보다 약 3.25배 더 빠르다.
- NVIDIA A6000과 같은 더 accessible한 GPU는 memory bandwidth가 훨씬 낮으므로 이 strategy가 더욱 effective하다: 2x A6000 GPU에서 3-bit OPT-175B model을 execute하면 FP16 inference (8 GPU에서)의 latency 589 ms에서 130 ms로 줄어들어, 4.5배의 latency reduction을 achieve한다.
-

Zero-Shot Tasks
-
우리의 focus는 language generation이지만, quantized model의 performance를 몇 가지 popular zero-shot task에서도 evaluate한다.
-
LAMBADA (Paperno et al., 2016), ARC (Easy and Challenge) (Boratko et al., 2018), PIQA (Tata & Patel, 2003)에서 평가한다.
-
실험 결과
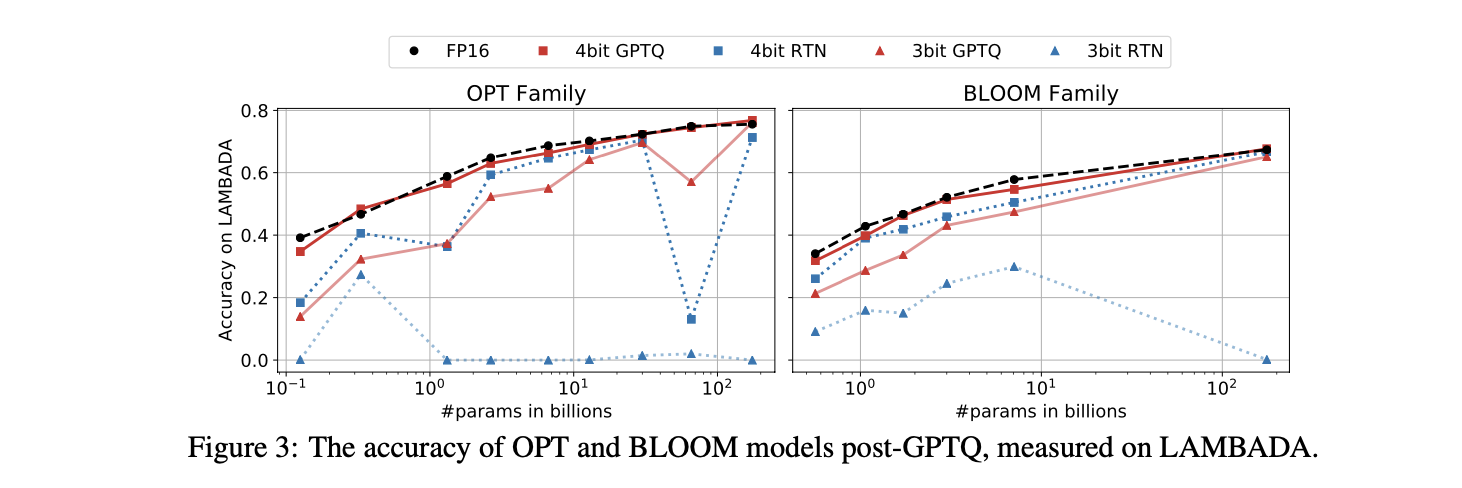
- Figure 3은 LAMBADA에서의 model performance를 visualize한다.
- 4-bit에서는 전체 spectrum의 model에 걸쳐 quantization이 "더 쉬워" 보이며, RTN 조차 성능이 좋다.
- 3-bit에서는 RTN이 breakdown되지만, GPTQ는 여전히 good accuracy를 보인다.
- Appendix A.4에 추가적인 결과
Additional Tricks
-
지금까지의 실험은 vanilla row-wise quantization에 focus했지만, GPTQ가 본질적으로 어떤 quantization grid 선택과도 compatible함을 강조한다.
-
예를 들어, GPTQ는 standard grouping (QSGD(Alistarh et al.), 2017; nuQmm(Park et al., 2022))과 쉽게 combine될 수 있다. 즉, g개의 consecutive weight group에 independent quantization 하는 것이다.
-
실험 결과
- Table 5: 마지막 row에서 보여지듯이, 3-bit에서 largest model에 대해 accuracy를 추가로 향상했다.
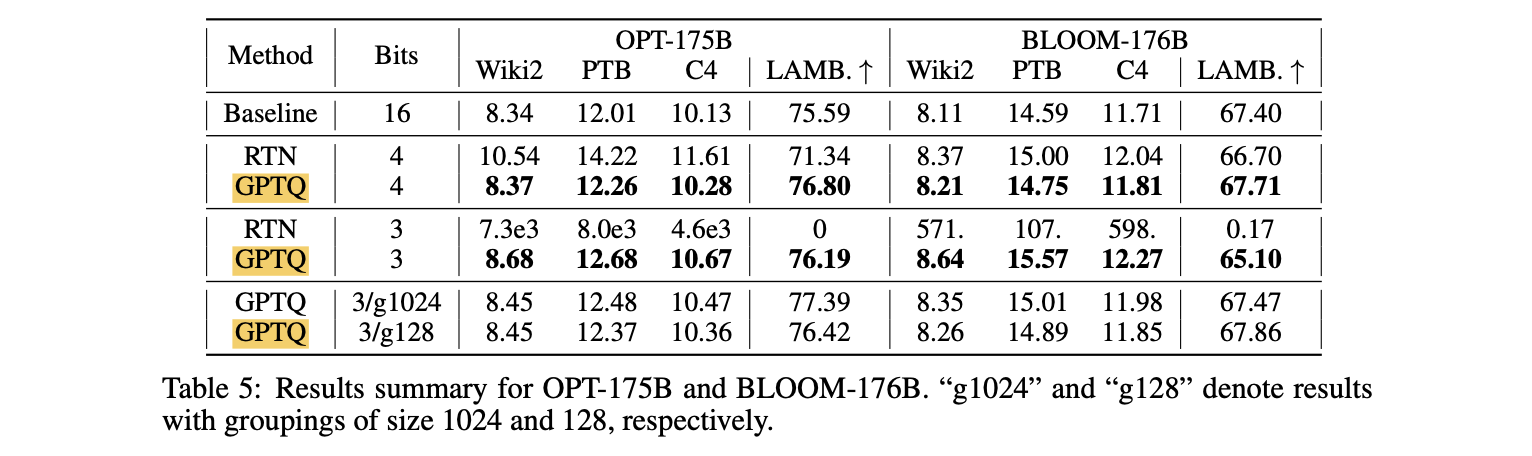
- Figure 4: 4-bit precision에서 medium sized model의 accuracy loss를 크게 줄인다.
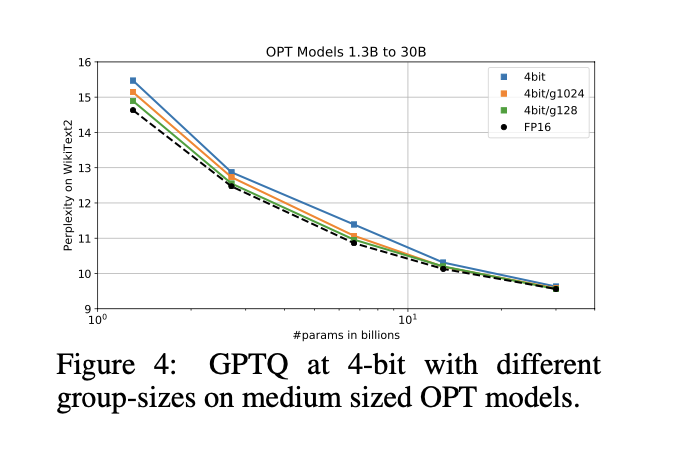
- Table 5: 마지막 row에서 보여지듯이, 3-bit에서 largest model에 대해 accuracy를 추가로 향상했다.
Extreme Quantization
-
grouping은 extreme quantization, 즉 평균적으로 component당 약 2-bit로 reasonable performance를 achieve하는 것을 가능하게 한다.
-
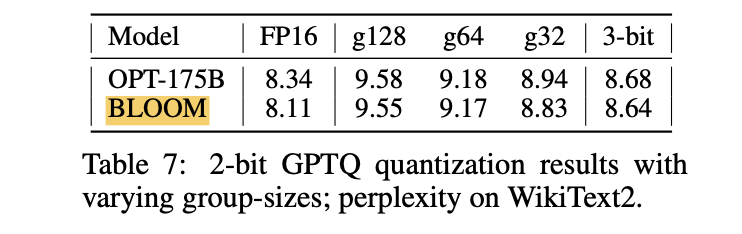
Table 7은 가장 큰 model들을 varying group-size로 2-bit로 quantize할 때 WikiText2에서의 결과를 보여준다.
- ≈ 2.2 bit (group-size 128; group당 FP16 scale과 2-bit zero point 사용)에서 perplexity 증가는 1.5 point 미만
- ≈ 2.6 bit (group-size 32)에서는 0.6 - 0.7로 감소. (이는 vanilla 3-bit보다 slightly worse)
-
group size를 8로 reduce하면, ternary (-1, 0, +1) quantization 적용 가능.
- OPT-175B에서 9.20 WikiText2 PPL을 achieve하며, 1 point 미만의 drop
- 위의 2-bit number에 비해 평균적으로 성능이 떨어지지만, FPGA와 같은 custom hardware에서 효율적으로 구현될 수 있다.
SUMMARY AND LIMITATIONS
SUMMARY
- GPTQ는 publicly-available한 가장 큰 model 중 일부를 3-bit와 4-bit로 accurately compress할 수 있다.
LIMITATIONS
1. 기술적 측면에서, 메모리 이동 감소를 통해 속도 향상을 얻지만, 실제 연산량(computation) 자체를 줄이지는 않는다.
- generative task에 focus하며, activation quantization을 고려하지 않는다.
이들은 future work를 위한 direction이며, 이것이 carefully-designed GPU kernel과 다음의 existing technique를 통해 achieve될 수 있다고 믿는다.
- ZeroQuant: Efficient and Affordable Post-Training Quantization for Large-Scale Transformers (Yao et al., 2022)
- Extreme Compression for Pre-trained Transformers Made Simple and Efficient (Wu et al., 2022)
