code

1. Introduction

Contribution

• layer-wise weight Q (PTQ)

• layer $l$에 대해, weights $\bold{W}_l$, layer inputs $\bold{X}_l$이고, compressed weights를 $\hat{\bold{W}}_l$라고 하면,
  original layer와 compressed layer 간의 squared error를 minimize하는 $\hat{\bold{W}}_l$를 찾는 것이 목표이다.

  $||\bold{W}_l\bold{X}_l - \hat{\bold{W}}_l\bold{X}_l||^2_2$

  (under fixed compression constraint on $\hat{\bold{W}}_l$)

• OBQ 연구는 위 문제에 특화된 framework를 통해, 어떠한 approximain을 사용하지 않고,
  기존에 직접적인 구현은 $\theta(d^4)$ ($d$: layer dimension)이 소요되는 것을,
  $O(d \cdot d^2_{col})$ ($d_{col}$: weight matrix column dimension)으로 계산 비용을 크게 줄이는 알고리즘을 제시한다.

• 각 step마다 (Loss 증가에 미치는 영향에 따라) 하나의 weight를 Q하고, Q되지 않은 나머지 weight들을 update하여 Loss를 더욱 감소시키는 OBQ greedy 전략을 사용한다.
  이는 수천만 개의 parameter를 가진 modern DNN의 scale에서, single GPU로 합리적인 시간 내에 수행 가능하다.

---

2. Related Work

PTQ

• AdaRound, AdaQuant, BRECQ VS OBQ
  $\\$
  AdaRound, AdaQuant, BRECQ: sequential layer Q
  layer를 sequential order로(순차적으로) Q.
  목적: 초기 layer에서 누적된 error를 후속 layer의 weight 조정으로 compensation.
  장점: 성능 개선.
  단점: flexibility 감소. 한 layer의 compression parameter를 변경하려면 전체 과정을 다시 수행해야한다.
  $\\$
  OBQ: independent layer Q
  각 layer를 independent하게 Q.
  장점: layer별(layer-wise) 결과를 단순히 "연결(stitched)"하여 최종 모델 구성 가능하여, flexibility 증가.
  각 layer를 independent하게 처리함에도 불구하고, BN과 같은 statistics를 보정한 후
  uniform quantization에 대해 sequential order 방법들과 대등한 성능을 보인다.

---

3. Problem Definition and Background

Layerwise Compression Problem

• 이전의 PTQ 연구들(AdaRound, AdaQuant)을 따라, 문제를 다음과 같이 정의한다.
  
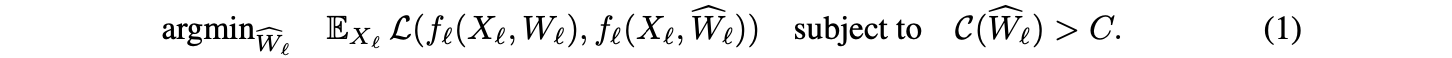
  수학적으로, layer $l$을 input $X_l$에 작용하는 함수 $f_l(X_l,W_l)$로 모델링하며, 이는 weight $W_l$에 의해 parametrized된다.
  $\\$
  Layer-wise compression의 목표는 원래의 weight와 가능한 한 유사하게 수행되는 $W_l$ 의 "compressed" 버전을 찾는 것이다.
  $\\$
  더 formal하게 말하면, compressed weight $\hat{W}_l$은 어떤 loss $L$로 측정된 Expected layer output change를 최소화해야 하며,
  동시에 compression 유형에 따라 customized되는 generic compression constraint $C(\hat{W}_l) > C$를 만족해야 한다.

• Layer input $X_l$에 대한 Expectation은 $N$개 input sample로 구성된 작은 데이터셋들의 mean(평균)을 취함으로써 approximation 한다.

• 대부분의 연구 (BitSplit, AdaRound, AdaQuant)는 linear 형태로 unfolded될 수 있는 linear layer와 convolutional layer 를 compress하는 데 focus를 맞추고 있다. 이는 이러한 layer들이 실제로 널리 사용되고 있기 때문이고, approximation error를 측정하기 위해 squared loss를 사용한다. 이 squared loss는 second-order information으로부터 일련의 approximation을 통해 유도된다.

1. 전체 network의 Loss 변화
   $\Delta{L} = L(\hat{W}) - L(W)$
   whrer, $W$: original parameter, $\hat{W}$: quantized parameter

---

2. Taylor 전개
   $\Delta{L} \approx \nabla{L(W)^T}(\hat{W}-W) + \frac{1}{2}(\hat{W}-W)^T\nabla^2{L(W)}(\hat{W}-W)$

---

3. Hessian 근사
   Hessian$(\nabla^2{L(W)})$를 Fisher Information Matrix로 approximation
   $\nabla^2{L(W)} \approx \mathbb{E} [ \nabla{l} \nabla{l}^T ] = H$
   where, $l$: sample loss

---

4. Layer-wise 분해
   네트워크를 layer별로 분해하고, 각 layer의 output 변화를 $δy$로 표현하면:
   $\nabla{L} \approx \sum_{layer}\mathbb{E}[δy^THδy]$
   where, δy: 각 layer의 output 변화

---

5. layer output 변화(δy) 근사
   $δy \approx \hat{W}x - Wx = (\hat{W}-W)x$
   where, $x$: 해당 layer로 들어가는 input

---

6. 최종 형태
   이를 $\Delta{L}$에 대입하면,
   $\Delta{L} \approx \sum_{layer}{\mathbb{E}(\hat{W}x - Wx)^TH(\hat{W}x - Wx)}$
   이때, Fisher Information Matrix $H$가 identity matrix와 유사한 성질을 가진다고 가정하면,
   이 식을 다음과 같이 단순화할 수 있다.
   $\Delta{L} \approx \sum_{layer}{\mathbb{E}[||\hat{W}x - Wx||^2]}$
   이로써, 각 layer에 대한 objective function이 다음과 같이 된다.
   $\mathbb{E}[||\hat{W}x - Wx||^2]$

• OBQ도 이 convention을 따르며, 아래 수식으로 정의된 layer-wise compression problem을 다룬다.
  
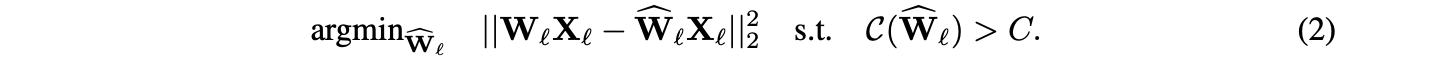
  weights $\bold{W}_l$ has dimensions $d_{row} x d_{col}$
  (conv layer의 경우 $d_{col}$은 single filter에 속한 weight의 total 개수이다)
  input $\bold{X}_l$ has dimensions $d_{col} \times N$

---

OBS Framework

OBS(Optimal Brain Surgen) framework는 훈련된 dense neural network를 정확하게 pruning하는 문제를 다룬다.
OBS framework는 주어진 지점에서의 Taylor approximation에서 시작하고 (이 지점에서 gradient는 무시할 수 있다고 가정한다), 제거할 optimal single weight와 이 제거를 compensation하기 위한 remaining weight의 optimal update에 대한 공식(formula)를 제공한다.

더 정확히 말하면, $\bold{H}$를 주어진 (dense) model에서의 loss의 Hessian matrix라고 하면, loss의 증가를 최소로 야기하는 pruning할 weight $w_p$와 이에 대응하는 remaining weight의 update $δp$는 다음과 같이 계산될 수 있다.

---

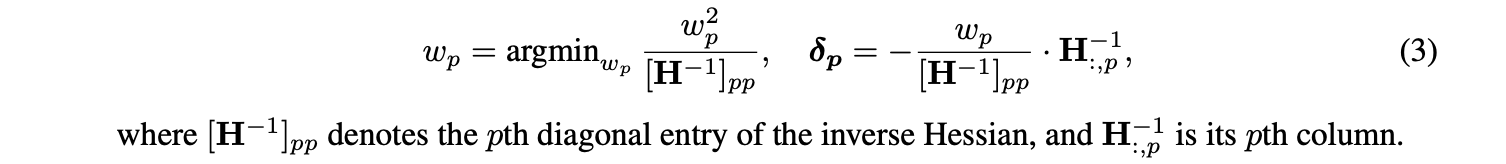
OBS for Layer-Wise Pruning

OBS framework를 앞서 정의한 layer-wise pruning 문제에 적용할 것이다.

1. Equation (2)의 loss는 quadratic 형태이다.
   
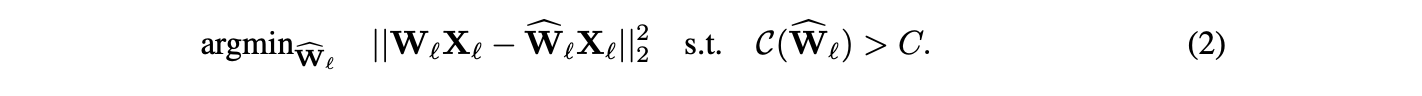
2. 우리의 시작점은 최소 loss인 0을 달성하는 dense weight이다.

이 조건들은 OBS framework의 가정을 완벽히 만족시키므로, 이 문제에 대해 OBS framework의 공식들이 정확히 들어맞는다.
따라서 OBS framework를 반복적으로 적용하여 한 번에 하나의 weight를 제거하면, layer-wise pruning 문제에 대한 정확한 greedy solution을 얻을 수 있다. 이 방법은 각 단계에서 locally 최적의 결정을 내리기 때문이다.
이 greedy approach가 global optimum을 보장하지는 않지만, 정확한 방법으로 다루기에는 너무 큰 문제들을 효과적으로 해결할 수 있다.

---

4. An Optimal Greedy Solver for Sparsity

분명한 문제는 OBS 프레임워크를 원래의 형태로 적용하는 것, 즉 Equation (3)의 true form을 사용하여 한 번에 하나의 가중치를 pruning하는 것이 계산적으로 매우 부담스럽다는 것이다.

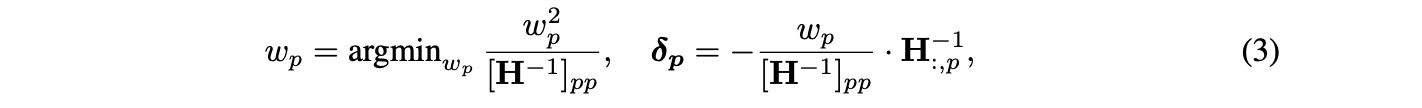
Weight의 dimension을 d{row}, d{col}이라고 할 때,
Hessian $\bold{H}$는 $d \times d$ matrix 이다. (where $d = d_{row} \cdot d_{col}$)
❗❗저장하고 계산하는 데 이미 비용이 많이 든다.

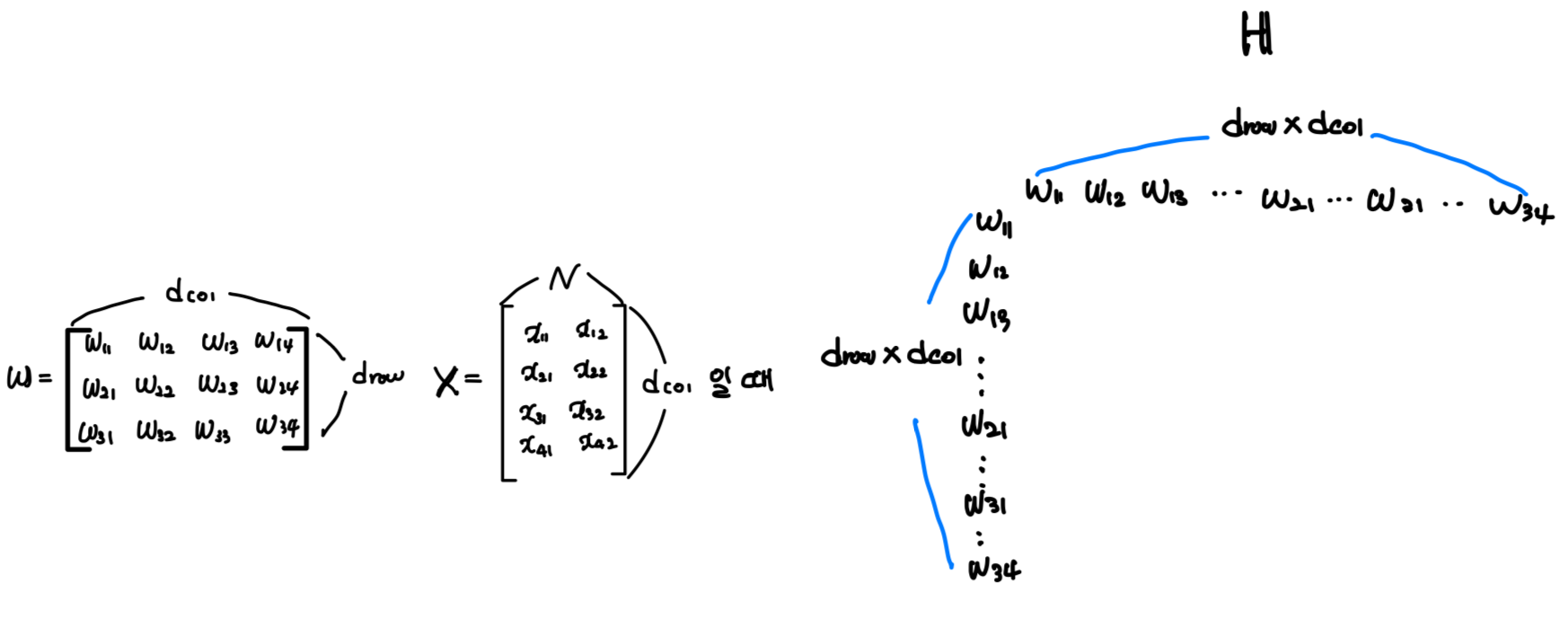
또한, Hessian matrix $\bold{H}$는 각 $O(d)$ step에서 $Θ(d^3)$의 계산 복잡도로 업데이트되고 역행렬이 계산되어야 한다. $O(d^4)$의 총 실행 시간은 현대 신경망의 대부분 층을 pruning하기에는 너무 비효율적이다. $d$는 여러 층에서 $10^5$ 이상이거나 심지어 $10^6$ 이상이기 때문이다.

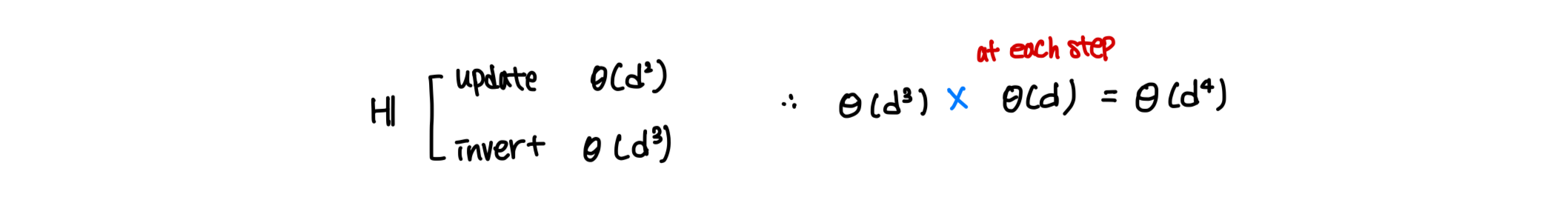
그러나 OBC 연구에선 이 과정의 전체 비용을 $O(d_{row} · d^3_{col})$ 시간과 $Θ(d^2_{col})$ 메모리로 줄였다.

이는 ResNet50과 같은 중간 크기의 모델의 모든 층을 단일 NVIDIA RTX 3090 GPU에서 1시간 조금 넘게 pruning하기에 충분히 효율적이다.
또한, 이전 연구(WoodFisher)와 달리, 우리는 어떠한 근사에도 의존하지 않기에, OBC의 technique들이 정확하다는 점을 강조한다.

---

ExactOBS Algorithm

layer-wise compression 문제에 대한 OBS framework의 efficient한 구현을 단계별로 소개한다. 이를 ExactOBS라고 부른다.
Equation (2)의 matrix squared error를 weight matrix의 각 row에 대한 squared error의 sum으로 objective function을 다시 작성한다.

항상 고정된 layer $l$을 다루고 있으므로, 표기를 간단히 하기 위해 아래 첨자 $l$을 생략한다.

이 방식은

• single weight $W_{ij}$를 제거하는 것이 해당 output row $\bold{Y_{i,:} = W_{i,:}X}$의 error에만 영향을 미친다는 것이 명확해진다.

• 따라서 서로 다른 row 간에는 Hessian 상호작용이 없으며, $d_{row}$의 row 각각에 해당하는 개별 $d_{col} × d_{col}$ Hessian들만으로 작업하면 충분하다.

• 또한, dense layer output $\bold{Y = WX}$가 fixed되어 있으므로, 각 row에 대한 objective function은 standard least squares form을 가지며 그 Hessian은 $\bold{H = 2XX^T}$로 주어진다.
  

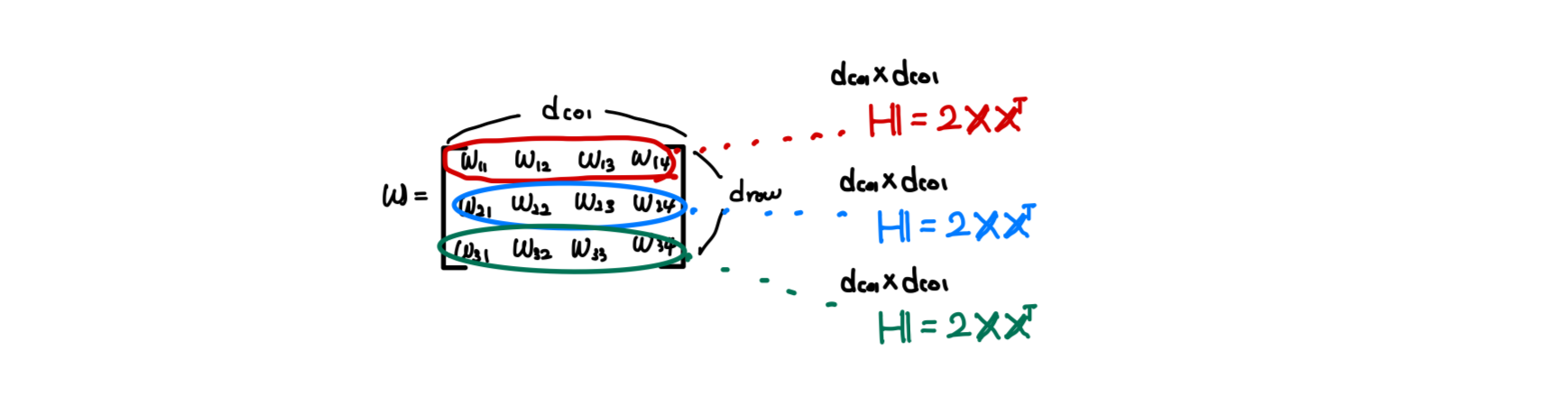
이 관찰이 이미 계산 복잡도를 줄이지만, 두 가지 주요 과제가 남아 있다.
(a) 각 row에 OBS를 적용하는 것은 여전히 $O(d_{col} · d_{col}^3)$ 시간이 소요되며, 이는 큰 layer에 대해 너무 느리다.

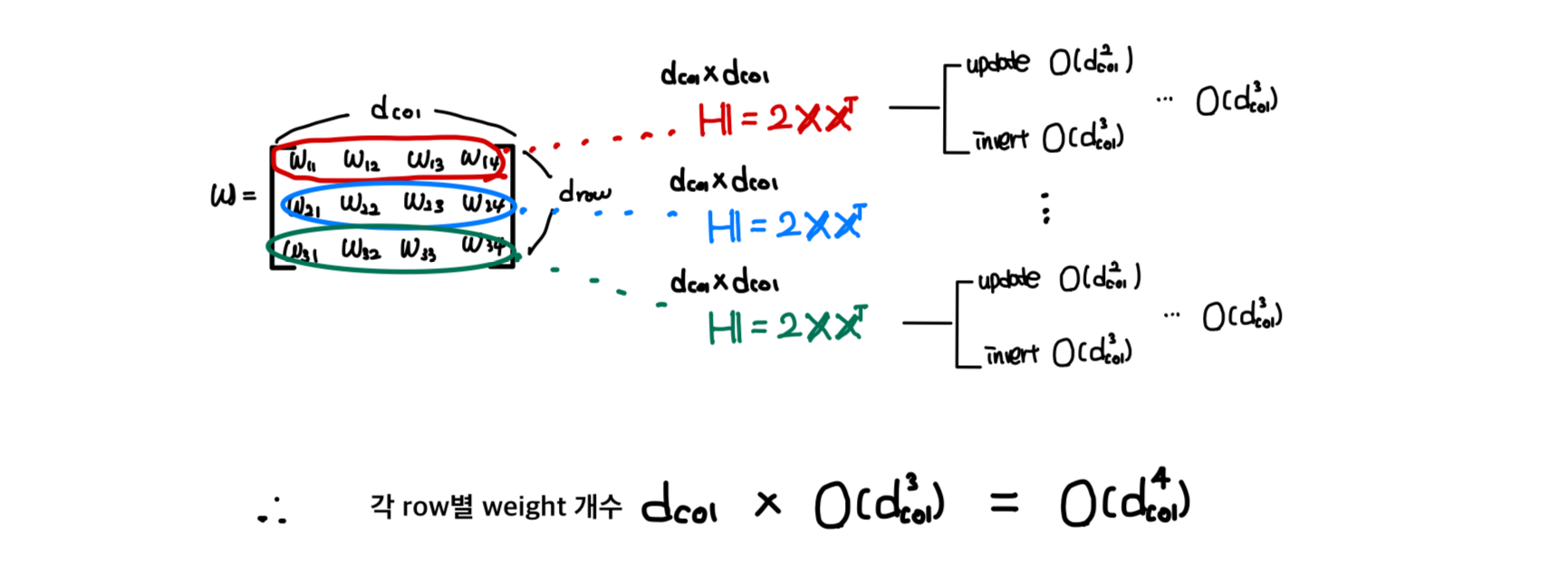
(b) 각 step에서 단순히 row 별로가 아니라, 전체 matrix의 minimum score weight를 pruning하고자 하므로, 모든 $d_{row}$개 row의 Hessian inverse에 빠르게 접근해야 한다.
특히, (b)는 $O(d_{row} · d_{col}^2)$ GPU memory를 필요로 하며, 이는 실현 불가능할(infeasible) 가능성이 높다.

---

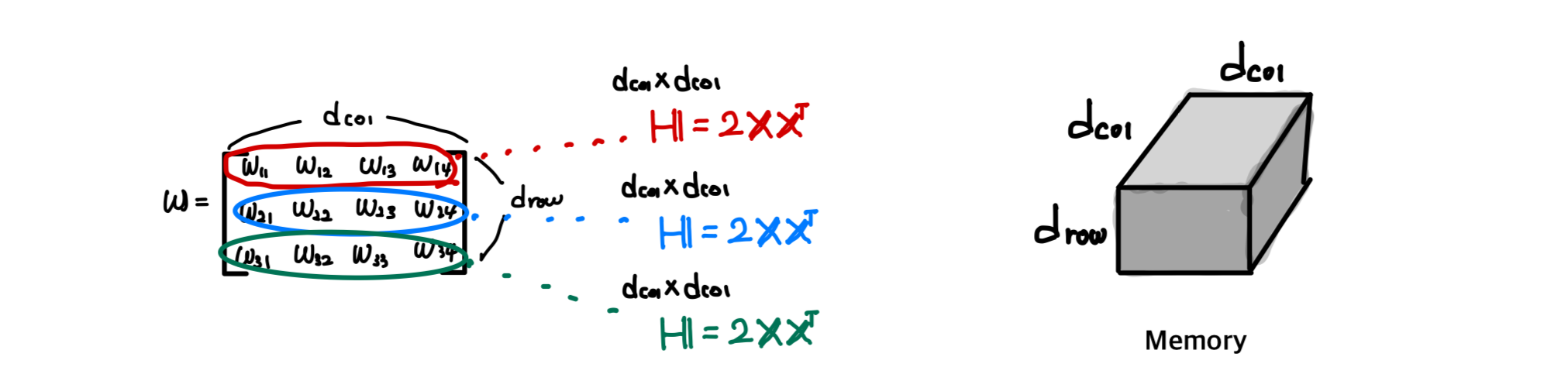
Step 1: Handling a Single Row

$d_{col}$개의 parameter를 가진 single row에서 efficient하게 weights를 prune하는 법을 설명한다.
전체 알고리즘은 Algorithm 1과 같다. ($\bold{w}$: row, $\bold{H}$: Hessian )

"Problem"
연산량이 너무 많다!
Problem 1.매 step마다 Hessian $\bold{H}$ update($\bold{H}=2\bold{XX}^T$)를 위해, 연산 $Θ(N\cdot d_{col}^2)$ 소요.
Problem 2.매 step마다 Hessian $\bold{H}$ inverse를 위해, 연산 $\Theta(d_{col}^3)$ 소요.

"Soltuion"
1.Hessian $\bold{H}$ update
기존: 매 step마다 $\bold{H}=2\bold{XX}^T$ calculation: $\Theta(N\cdot d_{col}^2)$
$\textcolor{red}{OBS: \ 처음 \ 한 \ 번만 \ Θ(Nd_{col}^2) \ 계산 \ 수행, \ 이후 \ pruning \ mask를 \ 사용하여 \ Θ(d_{col}^2) \ 연산으로 \ 필요한 \ 부분만 \ 추출}$

2.Hessian $\bold{H}$ inverse
기존: 매 step마다 $\bold{H}^{-1}$ calcuation: $\Theta(d_{col}^3)$
$\textcolor{red}{OBS: Gaussian \ 소거법을 \ 활용하여 \ Θ(d_{col}^2) \ 연산으로 \ \bold{H}^{-1} \ update}$

"Example"
🟨 1번 문제인 각 step에서 Hessian을 update해야 하는 문제의 해결은 쉽다.
각 step마다 계산하지 않고, H를 한 번만 계산하고,
pruning mask $M$에 따라 $H$에서 필요한 행과 열만 추출하는 방법을 사용할 수 있다.

예를 들어, 5x5 크기의 Hessian 행렬 $\mathbf{H}$가 있다고 가정해 봅시다.

$\mathbf{H} = \begin{bmatrix} h_{11} & h_{12} & h_{13} & h_{14} & h_{15} \\ h_{21} & h_{22} & h_{23} & h_{24} & h_{25} \\ h_{31} & h_{32} & h_{33} & h_{34} & h_{35} \\ h_{41} & h_{42} & h_{43} & h_{44} & h_{45} \\ h_{51} & h_{52} & h_{53} & h_{54} & h_{55} \end{bmatrix}$

그리고 pruning mask $M$이 [1, 0, 1, 0, 1]이라고 가정해봅시다.
여기서 1은 유지할 가중치를, 0은 제거할 가중치를 나타냅니다.
이 경우, $\mathbf{H}_M$은 다음과 같이 구성됩니다:

$\mathbf{H}_M = \begin{bmatrix} h_{11} & h_{13} & h_{15} \\ h_{31} & h_{33} & h_{35} \\ h_{51} & h_{53} & h_{55} \end{bmatrix}$

이 과정에서 우리는:
1. $\mathbf{H}$를 한 번만 계산합니다 (모든 행에 대해 동일).
2. pruning mask $M$에 따라 $\mathbf{H}$에서 필요한 행과 열만 추출합니다.
3. 이렇게 하면 매번 $\mathbf{H}$를 새로 계산할 필요 없이, mask에 따라 필요한 부분만 빠르게 추출할 수 있습니다.

🟨 2번 문제인 각 step마다 Hessian의 inverse를 구하는 문제의 경우, 이 trick을 적용할 수 없다. $(\bold{H}_M)^{−1} ≠ (\bold{H}^{−1})_M$이기 때문이다.
그러나 매개변수 $p$ 하나를 제거하면 $\bold{H}$에서 해당 row와 col이 단순히 제거된다는 사실을 이용하여, 가우스 소거법의 single step을 사용하여 parameter $p$를 직접 제거하도록 역행렬을 update 할 수 있으며, 이는 $Θ(d^2_{col})$의 비용이 든다.
$\footnotesize\textcolor{red}{다음 \ 결과는 \ 이를 \ 형식화하며,\ 그\ 증명은 \ Appendix에 \ 있습니다.}$

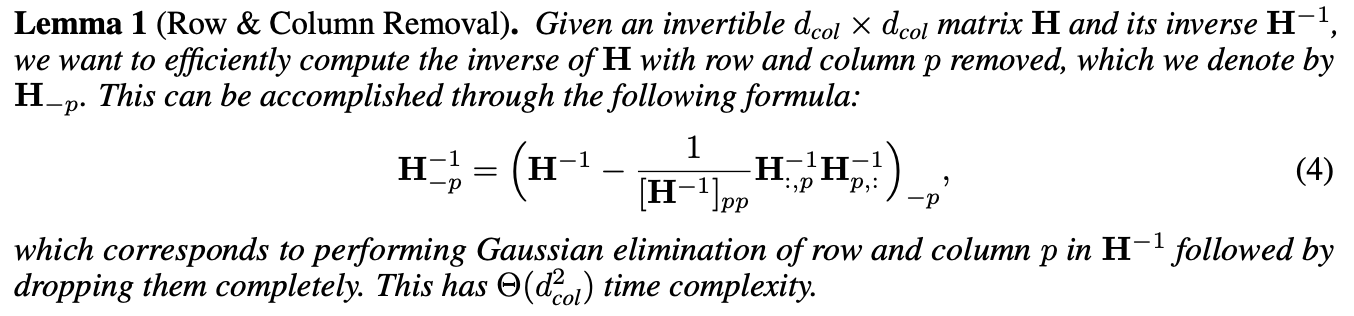
결과 pseudocode는 Algorithm 1과 같다.

여기서 $\bold{H}^{−1}$의 크기를 변경하지 않고 원래 크기를 유지한다.
이는 Lemma 1(보조정리 1)에 의해 row와 column $p$가 제거된 후에는 0이기 때문에(그리고 0이 아닌 대각선 요소는 다시 사용되지 않기 때문에) 이후 계산에 영향을 미치지 않기 때문이다.
이 알고리즘이 $W$의 single row에 OBS를 적용하며 per-step cost가 $Θ(d^2_{col})$이고,
따라서 $k$개의 가중치를 pruning하는 데 총 $Θ(k · d^2_{col})$의 시간이 걸린다.

예를 들어, 5x5 크기의 역 Hessian 행렬 $\mathbf{H}^{-1}$이 있다고 가정해 봅시다:
$\\$

$\mathbf{H}^{-1} = \begin{bmatrix} h_{11} & h_{12} & h_{13} & h_{14} & h_{15} \\ h_{21} & h_{22} & h_{23} & h_{24} & h_{25} \\ h_{31} & h_{32} & h_{33} & h_{34} & h_{35} \\ h_{41} & h_{42} & h_{43} & h_{44} & h_{45} \\ h_{51} & h_{52} & h_{53} & h_{54} & h_{55} \end{bmatrix}$

$\\$
1. 첫 번째 pruning 단계:

• 예를 들어, 세 번째 가중치(p=3)를 제거한다고 가정합니다.
• Lemma 1을 적용하여 3번째 행과 열을 0으로 만듭니다.
• 결과:
  $\begin{bmatrix} h'_{11} & h'_{12} & 0 & h'_{14} & h'_{15} \\ h'_{21} & h'_{22} & 0 & h'_{24} & h'_{25} \\ 0 & 0 & h'_{33} & 0 & 0 \\ h'_{41} & h'_{42} & 0 & h'_{44} & h'_{45} \\ h'_{51} & h'_{52} & 0 & h'_{54} & h'_{55} \end{bmatrix}$

2. 이후 단계:
   • 3번째 행과 열은 모두 0이므로($h'_{33}$ 제외) 이후 계산에 영향을 주지 않습니다.
   • 따라서 실제로는 4x4 행렬로 작업하는 것과 같습니다.
3. 계속된 pruning:
   • 각 단계마다 한 행과 열이 0이 되지만, 행렬 크기는 그대로 유지합니다.
   • 실제 계산은 점점 작아지는 부분행렬에서만 이루어집니다.
4. 계산 복잡도:
   • 각 단계에서 Lemma 1 적용: $\Theta(d^2_{col})$ 시간
   • k개 가중치 pruning: $\Theta(k \cdot d^2_{col})$ 총 시간

• 이 방법의 장점:
  • 행렬 크기 조정이나 인덱스 변경 없이 효율적으로 계산할 수 있습니다.
  • 매 단계마다 실제 계산되는 행렬의 크기가 줄어들어 효율성이 증가합니다.
  • 전체 과정이 $\mathbf{W}$의 단일 행에 대해 $\Theta(k \cdot d^2_{col})$ 시간에 OBS를 적용할 수 있게 합니다.

---

Step 2: Jointly Considering All Rows

"Problem"
OBS를 각 row에 independent하게 적용하는 것보다, 전체 weight matrix에 적용하는 것은 모든 row의 inverse Hessian에 빠르게 접근해야 하므로, memory 측면에서 비용이 많이 든다.
($d_{row}$ 개의 row별 $\bold{H}^{-1}$ ($d_{col} \times d_{col})$를 각각 GPU memory에 저장하는 것은 너무 비용이 많이 든다.)

"Insight"
그런데, row 간에 Hessian 상호작용이 없기 때문에, 다음의 두 insight를 이용한다.

• insight 1.각 row의 최종 결과는 해당 row에서 pruning된 parameter 수에만 의존한다.

• insight 2.일부 weight를 pruning함으로써 발생하는 loss의 변화는 같은 row에서 이전에 pruning된 weight에만 의존하며, 이는 각 row에서 weight가 pruning되는 순서가 고정되어 있음을 의미한다.

"Solution"
이러한 insight의 결과로, 각 row를 independent하게 처리하여 $Θ(d)$의 추가 memory만을 필요로 하는 방법을 제안한다.

• 모든 weight에 대해 loss 변화 $δL_p = w_p^2/H^{−1}_{pp}$를 계산하고 기록한다.

• 전체 weight matrix에 대한 global mask(pruning할 weight 표시)를 결정한다.

  • 모든 weight에 대해 계산된 $δL_p$ 값들 중 가장 작은 값부터 순서대로 선택한다.

• global mask에서 per-row mask $M_i$를 추출하여, 남은 weights들을 update한다.

  • group OBS 공식 $δ_{M_i} = H^{−1}_{:,M_i}((H^{−1})_{M_i})^{−1} \bold{w}_{M_i}$ 을 사용해 남은 weights를 update한다.
  • 이 방법은 Algorithm 1의 반복적 pruning 과정보다 빠르다.

"Example"

예를 들어, 3x4 크기의 weight matrix $\mathbf{W}$가 있다고 가정하자:

$\mathbf{W} = \begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} \\ w_{21} & w_{22} & w_{23} & w_{24} \\ w_{31} & w_{32} & w_{33} & w_{34} \end{bmatrix}$

여기서 $d = d_{row} \cdot d_{col} = 3 \cdot 4 = 12$
$\\$
1. 각 weight에 대한 δLp 계산:
우리는 각 weight를 pruning했을 때의 loss 변화 $δL_p$를 계산한다.
$δL = [δL_{11}, δL_{12}, δL_{13}, δL_{14}, δL_{21}, δL_{22}, δL_{23}, δL_{24}, δL_{31}, δL_{32}, δL_{33}, δL_{34}]$
$\\$
2. δLp 정렬:
이 값들을 오름차순으로 정렬한다. 예를 들어:
sorted ${δL} = [δL_{22}, δL_{13}, δL_{31}, δL_{24}, δL_{11}, δL_{32}, δL_{14}, δL_{21}, δL_{33}, δL_{12}, δL_{23}, δL_{34}]$
$\\$
3. global mask 생성:
pruning할 weight의 수(k)를 정했다고 가정하자 (예: $k=5$).
정렬된 리스트에서 처음 k개의 weight를 선택한다.
global mask = $[w_{22}, w_{13}, w_{31}, w_{24}, w_{11}]$
!! 이 과정은 원래 weight 개수 만큼의 추가 memory $Θ(d)$만 사용했다. !!
$\\$
4. per-row mask 추출
global mask $[w_{22}, w_{13}, w_{31}, w_{24}, w_{11}]$를 바탕으로 각 행에 대한 per-row mask를 추출한다.

• Row 1 $(w_{11}, w_{12}, w_{13}, w_{14})$: $M_1 = [1, 0, 1, 0]$ ➡️ $w_{11}$과 $w_{13}$이 pruning됨.
• Row 2 $(w_{21}, w_{22}, w_{23}, w_{24})$: $M_2 = [0, 1, 0, 1]$ ➡️ $w_{22}$와 $w_{24}$가 pruning됨
• Row 3 $(w_{31}, w_{32}, w_{33}, w_{34})$: $M_3 = [1, 0, 0, 0]$ ➡️ $w_{31}$만 pruning됨.
  여기서 0은 pruning된 weight를, 1은 유지된 weight를 나타낸다.
  $\\$
  5. 남은 weights 업데이트
• Row 1: $δ_{M_1} = H^{−1}_{:,M_1}((H^{−1})_{M_1})^{−1} \bold{w}_{M_1}$ 를 사용하여 나머지 $w_{12}$와 $w_{14}$를 업데이트
• Row 2: $δ_{M_2} = H^{−1}_{:,M_2}((H^{−1})_{M_2})^{−1} \bold{w}_{M_2}$ 를 사용하여 나머지 $w_{21}$과 $w_{23}$를 업데이트
• Row 3: $δ_{M_3} = H^{−1}_{:,M_3}((H^{−1})_{M_3})^{−1} \bold{w}_{M_3}$ 를 사용하여 나머지 $w_{32}$, $w_{33}$, $w_{34}$를 업데이트

대안으로, 충분한 CPU 메모리가 사용 가능하다면,
a) 각 row의 full pruning trace(pruning 단계에서의 weight 값들의 변화)를 CPU memory에 저장
b) 각 개별 pruning 단계 후의 full weight vector를 유지
c) 최종적으로 global mask에 해당하는 항목만 다시 load.
이는 $O(d_{row} · d^2_{col})$의 추가 CPU memory를 필요로 하지만,
pruning되지 않은 weight를 재구성하기 위한 두 번째 caclutation pass를 피할 수 있으므로 더 빠르다.

Figure 1은 CPU memory를 추가적으로 사용하는 옵션(Less compute)과 추가적으로 사용하지 않는 옵션(Less memory)을 비교한다.

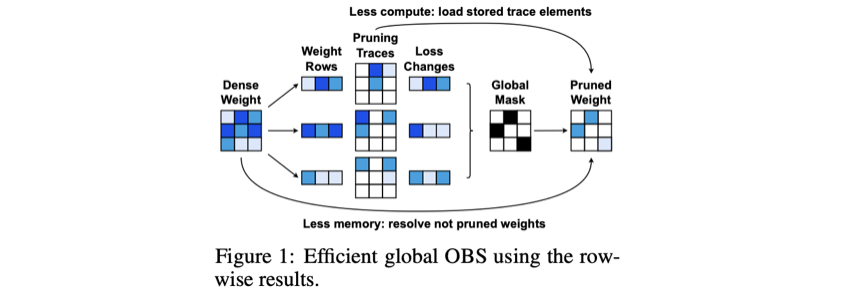
5. Optimal Brain Quantizer(OBQ)

classic한 OBS framework[23, 13]는 DNN을 pruning하는 많은 method 연구의 기반이 되었지만, quantization에는 사용되지 않았다. 본 연구에서 quantization에도 적용 가능함을 보이고, 이 method를 OBQ라고 부른다.

[23] Yann LeCun, Optimal brain damage. (1990)
[13] Hassibi, Optimal brain surgeon and general network pruning. (1993)

Quantization Order and Update Derivations

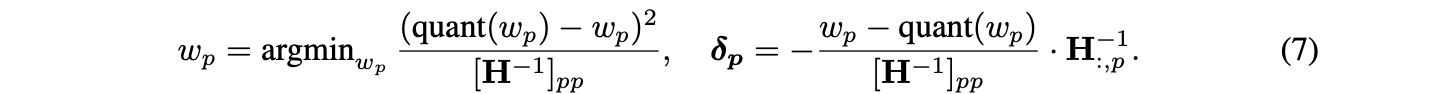
Quantizing Full Layers

얼핏 보면 OBQ는 이상해 보일 수 있다.
1. 다른 방법들은 주로 layer의 모든 weight를 quantize하여 더 이상 update할 weight가 남지 않는다.
2. OBQ의 weight를 선택하는 metric은 quantization order에만 영향이 있고, quantization value에는 영향이 없다.

하지만, OBC의 one-weight-at-a-time pruning 알고리즘의 맥락에서 고려하면 이러한 관점이 바뀐다. OBQ를 사용하면 metric에 따라 현재 "easiest"한 weight를 greedy하게 quantize한 다음, 남아있는 quantized되지 않은 모든 weight를 조정하여 이러한 loss of precision을 보상할 수 있으며, 이로 인해 weight value가 바뀌는 식으로 계속 진행한다.

이를 통해, 처음에 rounding을 통해 선택되었을 quantization assignment와는 다른 결과를 가져올 수 있으며, 전반적으로 더 나은 quantization 결과를 얻을 수 있다.

이를 구현하기 위해, Equation (7)을 Algorithm 1에 적용해 layer의 weights를 iterative하게 quantize할 수 있다.

그리고 Appendix의 Algorithm과 유사하게, 본질적으로 pruning과 quantization을 통합할 수 있다.

Quantization Outliers

OBQ의 greedy 방식의 한 가지 문제는, 현재 standard로 사용되는 방식인 "대다수의 weight에 대해 error를 더 낮추기 위해, 일부 outlier를 허용하는 quantization grid"에 적용될 때 발생할 수 있다.

outlier들은 주로 큰 quantization error를 갖기 때문에 마지막에 quantize 되며, 이 시점에는 이 error를 보상하기 위해 조정할 수 있는 (unquantized) weight가 거의 남아있지 않다.

OBQ는 quantizationerror가 > $\frac{∆}{2}$인 weight(여기서 $∆$는 양자화된 값들 사이의 거리)가 나타나는 즉시 quantize 하는 heuristic으로 이 문제를 방지한다.
(일반적으로 layer 당 적은 횟수만 발생한다).

Section 4에서 논의된 기술의 OBQ 버전은 모든 동일한 runtime 및 memory 특성을 가진다.
단, quantization의 경우, Figure 1의 glboal step은 불필요하다.
(pruning 에선 각 행에서 계산된 loss 변화 정보를 사용하여 전체적으로(global하게) 가장 적은 손실을 초래하는 방식으로 가중치를 선택하는데, quantization의 경우 각 행을 독립적으로 quantization 하는 것으로 충분하다는 뜻이다.)

6. Experiments

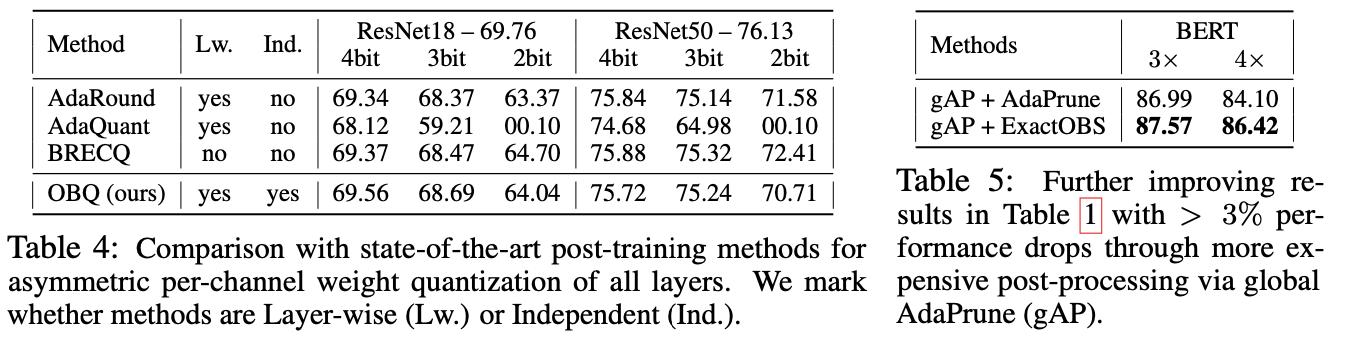
Experimental Setting

OBQ (독립적 수행)를 최신 순차적 post-training 방법들과 비교

• 비교 대상: AdaQuant, AdaRound, BRECQ
• Quantization 방식: asymmetric 채널별 weight quantization
• OBQ와 AdaRound의 quantization grid는 BRECQ와 동일한 Loss Aware PTQ 절차로 결정

Results
OBQ는 layer를 독립적으로 최적화함에도 불구하고, 4 bits와 3 bits에서 기존의 비독립적 방법들과 매우 유사한 (때로는 약간 더 나은) accuracy 달성.