Abstract

PTQ는 convenient하고 straghtforward한 model compression 접근으로, 2D vision task에 널리 채택되어 왔다.
하지만, 이를 바로 3D lidar-based task에 적용하는 것은 performance degradation을 유발한다.
따라서, 우리는 3D lidar detection (both SPConv-based and SPConv-free)에 paticularly curateded된 PTQ method인 LiDAR-PTQ를 제안한다.

LiDAR-PTQ는 세 가지 main components를 특징으로 갖는다.
1) quantization parameter의 initatilization을 결정하기 위한 sparisty-based calibration method

2) quantization 전후의 disparity를 줄여줄 Task-guided Global Positive Loss

3) laywerwise reconstruction error를 minimize하기 위한 adaptive rounding-nearest operation

Extensive한 experimetns를 통해 CenterPoint(both Pillar-based and Voxel-based)에 적용했을 때 SoTA 성능을 달성함을 증명했다.
lidar-based 3D detection tasks에서 가장 첫번째로, PTQ INT8 model의 accuracy가 FP32 모델과 거의 동일하며, inference speed를 3배 이상 향상했다.
더불어, LiDAR-PTQ는 QAT보다 30배 더 cost-effective하다.

코드는 공개 예정이라고 한다: https://github.com/StiphyJay/LiDAR-PTQ

Introduction

[LiDAR-based 3D Detection에서 Quantization의 필요성]
LiDAR-based 3D detection은 self-driving과 robotics의 다양한 범위의 application에 사용되고 있다. 주변 환경에서 obejct를 빠르고 정확하게 detect하는 것이 중요하다. 즉, performance와 latency 두 개 모두 요구된다.
현재, grid-based 3D detector들의 mainstream은 irregular한 point cloud를 arranged grids(voxels/pillars)로 convert한다. 최고 성능을 보이고 있지만, resource-limited edge device에 deploy하는 데에는 crucial challenge를 마주하고 있다.
따라서, grid-based 3D perception methods의 efficiency를 향상하는 것이 중요하다.
(e.g. memory와 computation cost를 줄이기)

[PTQ를 사용하는 이유: QAT와 차이점을 중심으로]
QAT는 모든 labeled training data에 대한 access가 필요하고,
substantial한 computation resource가 요구된다.
반면 PTQ는 오직 적은 수의 unlabeled sample들이 calibration set으로 필요하기 때문에,
fast, effective한 industrial application들에 더욱 적합하다.
게다가, PTQ는 모든 가능한 labeled data로 network를 다시 training할 필요가 없기 때문에, Quantization process가 더 short하다.
RGB-based detection task들에 여러 advanced된 PTQ 방법들이 제안되었지만, image와 point cloud 간의 차이가 있기 때문에, 이를 3D lidar-based task에 직접 적용하는 것은 performance degradation을 피할 수 없을 것이다.

[LiDAR-based Quantization의 Challenges]

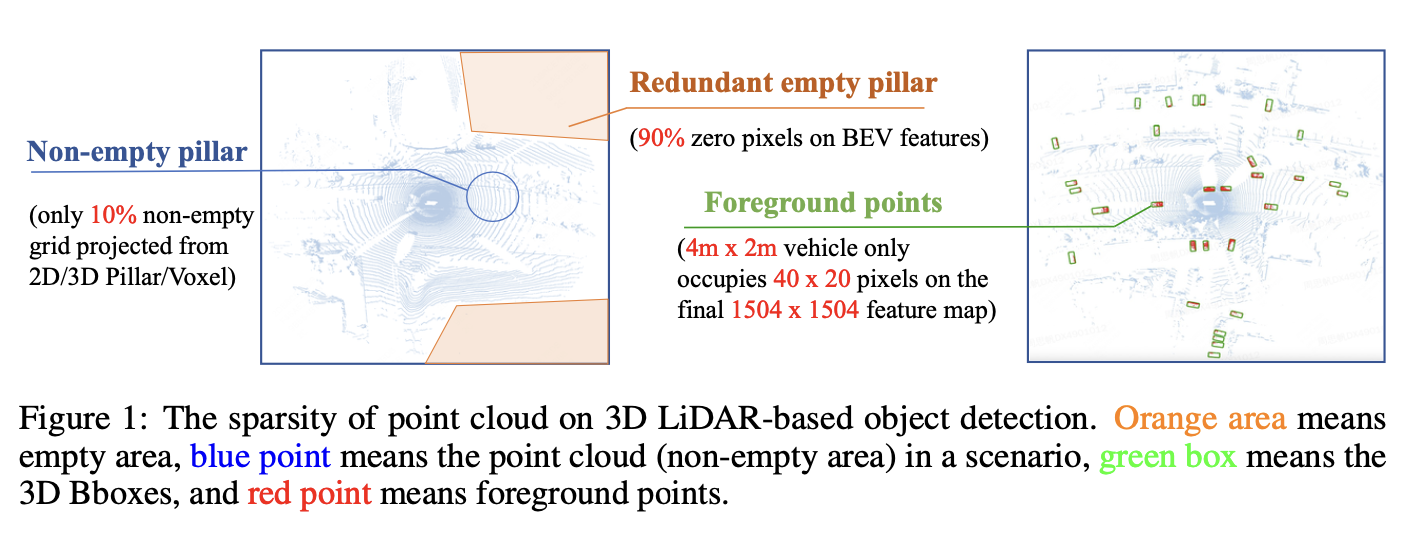
Fig 1에 보이는 것처럼, LiDAR point clouds의 sparsity와 irregular distribution은 3D Lidar-based detector를 quantization하는데 있어 new challenge이다.

(1) point cloud의 sparsity
dense한 RGB image와는 다르게, non-zero pixel은 전체 scene에서 오직 limited한 part만 차지한다.
(Waymo dataset에서는 10% 정도 차지한다)
예를 들어, 많은 수의 zero pixel으로 인해 dense한 RGB-based task와 비교해서 activation distribution에 큰 차이가 있다.

(2) larger arithmetic range
8-bit(0-255) RGB image와 비교해서,
Waymo dataset에서 voxelization 이후의 point 좌표는 1504 x 1504 x 40 (voxel size = 0.1m)의 3D space 안에 위치한다.
따라서 quantization의 clipping error와 같은 영향에 더욱 민감하다.

(3) foreground instnce와 large redundant한 background area 간의 Imbalance
예를 들어, CenterPoint-Voxel 모델 기반으로
input인 1504 x 1504 BEV feature map에서
4m x 2m 크기의 vehicle은 오직 40 x 20 pixel을 차지한다.
이렇듯 3D detection의 large한 perception range와 small한 foreground instance는 quantized된 model이 detection performance를 유지하기 위해 더 적은 information loss를 가져야 할 것이다.

이러한 challenge들이 2D vision task에서의 quantization 방법들이 3D point cloud task에 직접 적용하는데 장애물이 된다.

Preliminaries

[LiDAR-based 3D object detection]

3D space 안의 $N$ 개의 points가 주어질 때, point set은 다음과 같이 정의된다.
$\bold{P} = \{\bold{p}_i = [x_i, y_i, z_i, r_i]^T \in \mathbb{R}^{N \times 4}\}$
$x_i, y_i, z_i$: 각 point의 좌표값, $r_i$: laser reflection intensity

3D scene 안의 object set은 다음과 같이 정의된다.
$\bold{B} = \{\bold{b}_j = [x_j, y_j, z_j, h_j, w_j, l_j, \theta_j, c_j]^T \in \mathbb{R}^{M \times 8}\}$
$M$: total # of objects, $b_i$: $i$-th object in the scene,
$x_j, y_j, z_j$: object's center, $h_j, w_j, l_j$: object's size
$\theta_j$: object's heading angle, $c_j$: object's class

LiDAR-based 3D object detection의 task는 point cloud $\bold{P}$로부터 3D boxes $\bold{B}$를 accurate하게 detect하는 것이다.

[Quantizator for tensor]

quantization operation은 아래 수식을 따라서 floating-point value $x$ (weights 또는 activations)를 integer value $x_int$로 매핑하는 것이다.

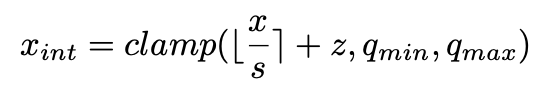
여기서 rounding-to-nearest 연산으로 rounding error $\Delta r$이 발생하고,
$clamp(\cdot)$으로 인해 clipping error $\Delta c$가 발생한다.
$z$: zero-point
$s$: quantization scale factor (FP value와 integer의 비율 관계를 나타냄)
$[q_{min}, q_{max}]$: quantization range (bit-width $b$로 결정됨)

우리는 uniform signed symmetric quantization을 선택했다, 왜냐하면 TensorRT에서 가장 폭넓게 사용되고 accelearation effect를 주기 때문이다.
따라서, $q_{min}=-2^{b-1}$ 이고 $q_{max}=2^{b-1}-1$이다.
Non-uniform quantization은 hardware에 deploy가 challenging하기 때문에 이 연구에선 무시했다.

*calibration: clipping range(quantization range)를 결정하는 과정
보통, weights는 calibration data 없이 quantized가 가능하다.
따라서, PTQ에서 weights는 보통 grid search 또는 MSE를 minimize하는 closed-form solution으로 analytical approximations을 사용한다.

하지만, activation quantization은 input-dependent하다.
따라서, range를 estimation해서 converge하기 위하여, 몇 개의 calibration data의 batch들이 필요하다. real-valued input $x$를 approximate하기 위해서, 우리는 de-quantization step을 수행한다.
$\hat{x}$가 de-quantized된 FP value로 quantization process에서 생긴 error를 포함한다.

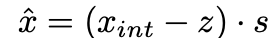
[Quantization range]
clipping error $\Delta c$를 줄이려면, quantization scale factor $s$를 키워서 quantization range를 크게 만들면 된다.
하지만, $s$를 키우는 것은 rounding error $\Delta r$을 증가시킨다.
따라서, clipping error와 rounding error 사이의 trade-off를 적절히 달성할 수 있는 quantization range $(x_{min}, x_{max})$를 정하는 것이 핵심적인 문제다.

구체적으로, fixed bit-width $b$를 정하면, scale factor $s$는 quantizatoin range에 의해 결정된다.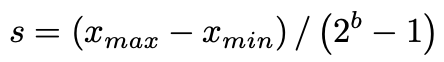
quantization range를 정하는 방법엔 크게 두 가지 보편적인 방법이 있다.

1) Max-min calibration

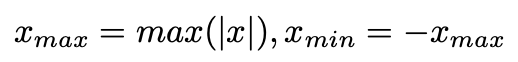
모든 fp value $x$의 range를 커버하기 때문에 clipping error가 존재하지 않는 방법이다.
하지만, 과도한 outlier에 민감한 방법이기에 과도한 rounding error를 유발할 수 있다.

2) Entropy calibration
TensorRT는 KL divergence를 기반으로 $x$와 $\hat{x}$ 사이의 information loss를 minimize하는 방식으로 quantization range를 정한다.

[Quantization for network]

$N$ 개의 layer를 가진 fp 모델에서, 우리는 중심적으로 weights와 activation을 handling하는 convolutional layer 또는 linear layerdml quantization에 focus한다.

$L_i$ layer가 주어질 때, weight와 input tensor에 quantization 연산을 수행한다.
결과적으로, layer의 quantized된 output은 아래와 같이 표현될 수 있다.

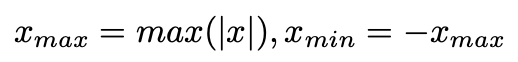
METHODOLOGY

[연구 필요성]
CenterPoint-Pillar 모델에 대해 PTQ ablation study를 진행했다.
Waymo val set에 대해 두 가지 다른 calibrators (Entropy와 Max-min)을 사용했다.
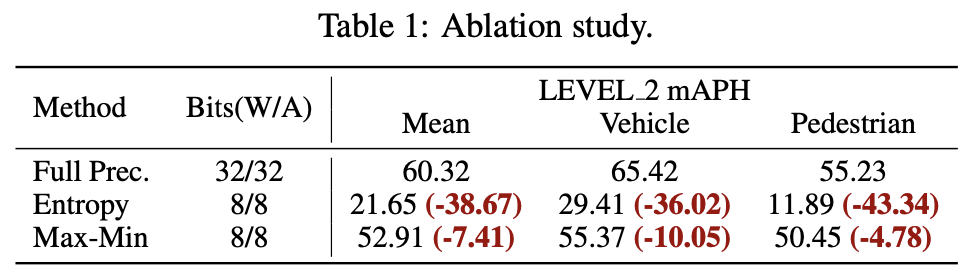
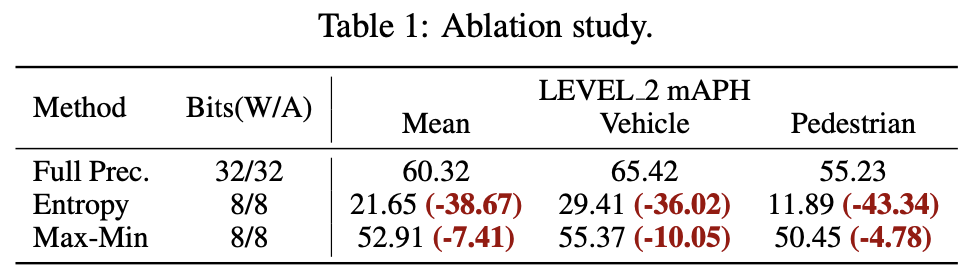
Table 1과 같이, INT 8 quantization을 사용했을 때, 특히 entropy calibrator를 사용했을 때 performance drop이 굉장히 컸다.
2D model quantization에서 두 calibrator를 사용했을 때 entrop calibration은 효율적으로 outlier의 영향을 줄임으로써 superior한 결과를 달성했던 것과는 완전히 대조적인 결과다.
이러한 이상 현상은 우리가 3D LiDAR-based detectors를 위한 PTQ method의 필요성을 보여준다.
(LEVE_2 mAPH는 mAP with Heading으로 Waymo dataset에서 널리 쓰이는 지표이다.)

3.1 LiDAR-PTQ Framework

1) Sparsity-based calibration
Max-min calibrator euqipped with a lightweight grid search를 사용해서
weights와 activations 모두에 대한 quantization parameters를 적절하게 initialize한다.

2) Task-guided Global Positive Loss
foreground-aware global supervision를 활용해 activation의 quantization parameter를 optimzie한다.

3) Adaptive rounding-to-nearest
weight rounding error $\Delta r$을 줄이기 위해 layer-wise reconstruction error를 minimize한다.

요약하면, LiDAR-PTQ는 먼저 parameter space에서의 search를 통해
weights와 activation의 quantzation parameters를 initialize한다.
그리고 model space 에서의 supervised optimization 과정을 거치면서 quantization parameters를 refine한다.
결과적으로, fp 모델의 accuracy와 거의 가깝게 quantized accuracy를 달성한다.

3.2 Sparsity-based Calibration

Tab 1의 Max-min과 entropy calibrator 사이의 큰 performance gap에 대한 원인을 파고들기 위해, RGB-based model과 LiDAR-based object detection model들의 feature maps distribution을 분석했고,
주요 diversity를 Fig 3에 시각화했다.

quantization performance에 영향을 주는 주요 원인은 두 가지 포인트로 요약될 수 있다.

1) Huge sparsity가 inappropriate한 quantization range를 초래했다.
Fig 1과 Fig 3에서 볼 수 있듯, point cloud의 sparsity가 전체 BEV feature map에 수많은 zero pixels가 존재하게 만들었다.
따라서, entropy calibrator will statistic the feature value including zero pixels(\approx 90%) to minimize the information loss,
그리고 이는 quantization range 바깥의 value들이 clipped 되도록 초래한다.
하지만, 이 버려지는 value들은 최종 object detection에 사용될 수 있었던 rich한 geometric representation을 갖고 있다.

2) Point cloud features가 quantization range에 더 sensitive하다.
point cloud는 spatial distances와 object의 shape을 측정한다.
voxelization 과정에서, raw point cloud 좌표 i.e. ego-vehicle 좌표계 안의$(x, y, x)$ 는 voexl features의 한 부분으로 encoded되어 필수적인 geometric information을 갖는다(preserve).
구체적으로, input point cloud 좌표의 arithmetic range는 detection distance에 비례해 증가한다. 그렇기에, voxel feature 안의 arithmetic range는 detecton distance와 끈끈하게 연관되어 있다. 다르게 말하면, point clouddml arithmetic range는 geometrics와 연관이 있다.

나아가서, 우리는 waymo val set에서 각기 다른 range distance들로 abliation study를 진행했다.
Tab 2에 보이는것과 같이, distance가 증가함에 따라 accuracy의 감소는 더욱 증가했다.
entropy calibrator에 대해서, long-range metrics (50m - $\infty$)의 quantized performance는 심각하게 손상됐다. (84.5% drop)
그런 반면에 short-range metrics의 accuracy는 그나마 괜찮게 유지됐다.
이것은 entropy calibrator가 inappropriate한 quantization range를 제공했기 때문에, 중대한 clipping error가 발생한 것이다.
따라서, 많은 수의 geometrics info를 가진 value들이 truncated되고, model accuracy가 substantial하게 degradation된 것이다.
반면, Max-min calibrator는, 모든 FP activation의 range를 커버하므로, geometric information이 효율적으로 보존되었다(preserved).
따라서, 각기 다른 range metric에서도 성능이 잘 나오는 것이다.

이러한 발견에 기초해서, 우리는 RGB image에 흔히 사용되는 calibration method(entropy calibrator)는 sub-optimal하고, Max-min이 3D point clouds에는 더 적합함을 결론지었다.
따라서, 우리는 Max-min calibrator를 weights와 activations에 모두 적용해서 high sparsity의 영향을 줄이고자 했다.
게다가, 더 finer-grained한 scale factor를 얻고 rounding error $\Delta r$ 에서의 outlier들의 영향을 피하기 위해서, light weight grid search를 함께 사용했다.
이를 통해 quantizawtion parameters를 더욱 optimize했다.

구체적으로, weight 또는 activation tensor $X$에 대해서,
먼저 $x_{max}$와 $x_{min}$을 얻는다.

$x_{max} = max(|x|), x_{min} = -x_{max}$

그리고 initial quantization parameter $s_0$를 계산한다.

$s=(x_{max} - x_{min})/(2^b - 1)$

그리고선 $[\alpha s_0, \beta s_0]$ interval을 $T$ 개의 후보 bins로 linear하게
divide한다.

$\{s_t\}^T_{t=1}$

$\alpha, \beta$ 그리고 $T$는 search range와 granularity를 control하기 위해 설계됐다.
최종적으로, ${s_t}^T_{t=1}$를 search해서 quantization error를 최소화하는 optimal한 $s_{opt}$를 찾는다.

3.3 Task Guided Global Positive Loss

앞서 본 calibration initialization 접근은 lidar detectors의 quantization accuracy를 향상할 수 있지만, 여전히 fp 모델과 비교했을 때 gap이 크다.

이전의 연구들에서 empirical 그리고 theoretical하게
단지 parameter space 안에서 quantization error를 최소화하는 것은 model space 안에서 final task loss를 최소화하는 것과 동일함을 보장하지 못함을 밝혀냈다.
따라서, 3D LiDAR-based detection task에 tailored된 global supervisory signal이 필요하다.
이 supervision은 quantization parameters $p$의 fine-tuning을 가능케 해서, 더 higher한 quantized precision을 달성할 수 있을 것이다.
이 fine-tuning process는 labeled training data를 필요로 하지 않는 다는 점도 강조할만 하다.
float output $O^f$ 와 quantized model의 output $\hat{O}$ 사이의 distance를 minimize하면 된다.

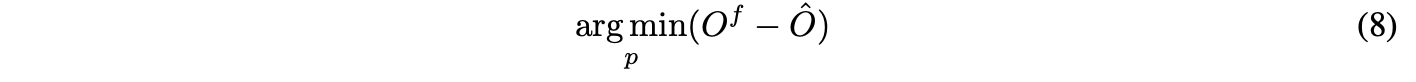
이 논문에서, 우리는 Task-guided Global Positive Loss 함수를 제안해서 quantized 모델과 FP 모델 간의 output disparity를 constrain하려고 한다.
우리의 TGPL 함수는 quantized 모델의 성능을 향상하는 두 가지 특성을 갖는다.

1) Optimal quantization parameter on model space

TGPL 함수는 각 layer의 output에서의 차이가 아닌 FP 모델과 quantized 모델의 final output 차이를 비교한다.

2) Task-guided
Lidar-based detection task에는
작지만 informative한 foreground instance와
크지만 redundant한 background area 간의 imbalance가 존재한다.

sparse한 3D scene에선, dense한 2D image의 모든 feature pixel을 따라하는 것은 sub-optimal하다.
TGPL 함수는 FP 모델의 classification response 안의 cue들을 leverage해서
quantized 모델이 final task와 연관된 중요한 area (i.e. positive sample location)에 focus하도록 guide하게 설계됐다.

구체적으로, FP 모델로부터의 prediction box들을 threshold $\gamma$를 이용해 모두 filter하고, top $K$ 개의 box들을 선택한다.
그리고선, NMS(Neubeck & Van Gool, 2006)을 수행해서 positive boxes(pseudo-labels)로 final prediction을 얻는다.
구체적으로, CenterPoint 모델의 Gaussian label assignment에 inspired돼서, 우리는 center-peak Gaussian distribution으로 positive position을 정의했다.
최종적으로, classification branch에서, 우리는 L1 Loss $L_{reg}$을 사용해서 그들의 localization offset, size, orientation을 supervise한다.
overall한 TGPL loss는 두 가지로 다음과 같이 구성된다.

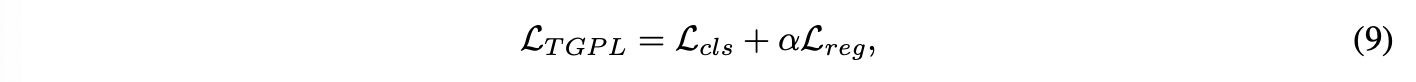
3.4 Adaptive Rounding-to-nearest

grid search initialization과 TGPL function constrain을 통해, quantized model의 performance는 크게 향상됐다.
하지만, 여전히 FP 모델과는 accuracy 차익가 꽤 있다.
최근, 몇몇 연구에서 rounding values라는 variable을 optimize한다. 이는 weight values를 quantization 과정에서 올림할 것인지, 내림할 것인지 결정하는 변수이다.
이 방식으로, weight quantization은 다음과 같이 공식화된다.

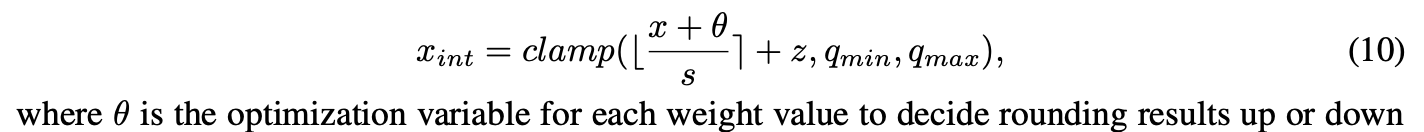
i.e. $\frac{\theta}{S}$ ranges from 0 to 1

AdaRound에서 영감을 받아, 우리는 rounding value $\theta$을 learning하기 위해, local reconstruction item을 추가했다.
local reconsruction item은 다음과 같다.
이 opeartion은 calibration data를 따라 information loss를 minimize하기 위해rounding value를 adapt하도록 해준다.
rounding value를 조정해서, 우리는 더 나은 성능을 가질 수 있다.

최종적인 overall loss는 아래와 같이 두 가지로 구성된다.

Experiments

Dataset
Waymo Open Dataset(WOD)

Implementation Details
Random하게 WOD의 training set에서 256 frames point cloud data를 calibration data로 샘플링
calibration set의 proportions는 WOD의 0.16% (256/158,081)를 차지한다.

first layer와 last lsyer는 full precision을 유지했다.
activation quantization scaling factor를 위한 learning rate은 5e-5이고,
weight quantization rounding을 위한 learning rate은 5e-3이다.
TGPL Loss에서, $\gamma$를 0.1, $K$를 500으로 설정했다.

4.1 Performance Comparison on Waymo Dataset

3D LiDAR-based detection task를 위해 특별히 설계된 PTQ methods들이 없기 때문에, 우리는 2D RGB-based vision task의 여러 PTQ method들을 reimplement했다.
BRECQ, QDROP, PD-Quant가 그것들이다.

특히, 잘 알려진 CenterPoint 모델을 full precision model로 선정했고,
WOD 데이터셋에 performance를 기록했다.
이 모델은 SPConv-based와 SPConv-free 모델을 포함하기 때문에, LiDRAR-PTQ 모델의 generalization을 verify하기에 효율적이다.

Tab 3에 볼 수 있듯, LiDAR-PTQ는 SoTA를 달성했다.

4.2 Effectivenetss of LIDAR-PTQ for Fully Sparse Detector

이 실험은 LiDAR-PTQ가 fully sparse detectors에도 적용 가능함을 증명한다.

최근, FSD와 FSD++, VoxelNet 등과 같이 fully sparse 3D detectors가 부상하고 있다.
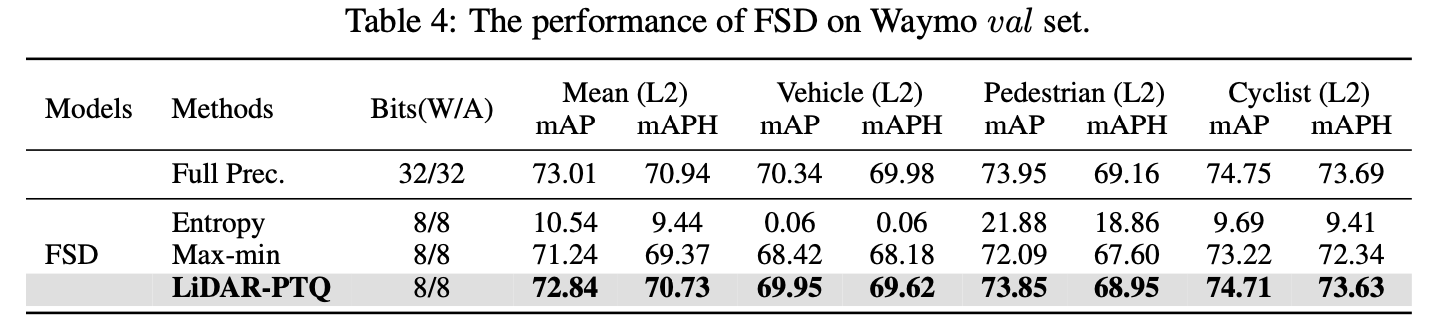
여기서, FSD를 예시로 LiDAR-PTQ의 effectivenetss를 validate했다.

Tab 4에서 볼 수 있듯, entropy calibration을 적용하는 것은 significant한 accuracy drop이 발생한다. (-61.50)
vanilla max-min calibration을 사용하는 것은 바람직한 성능을 가져옴을 발견했다.
그럼에도 불구하고, LiDAR-PTQ는 더 나은 성능을 보임을 알 수 있다.

4.3 Ablation Study

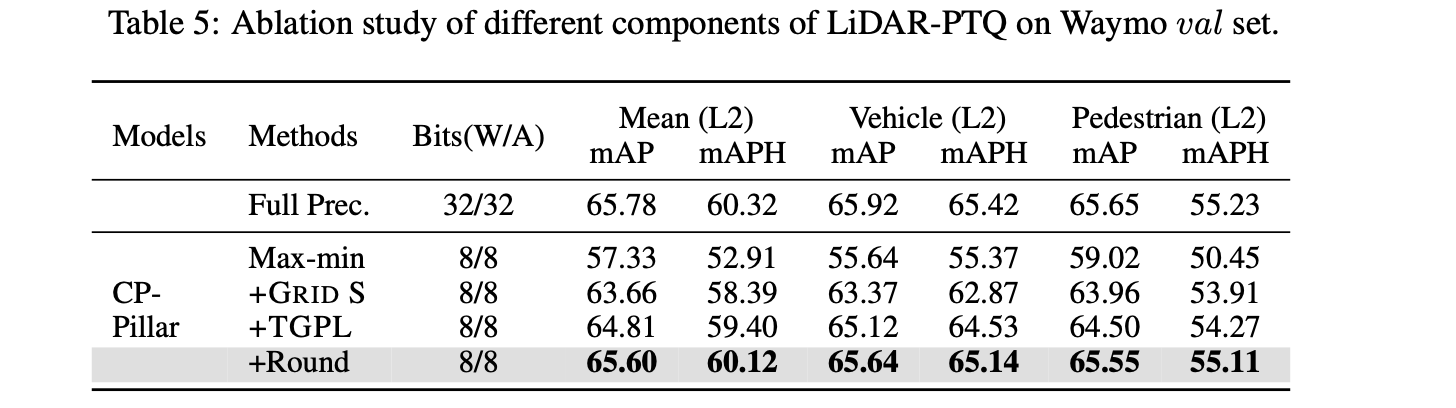
CenterPoint-Pillar model에서 LiDAR-PTQ 의 각기 다른 components의 effects를 verify하기 위해 ablation study했다.
Tab 5에서 볼 수 있듯, 우리가 선택한 Max-min calibrator를 기반으로,
lightweight grid search 방법을 사용해 5.48 mAPH/L2 성능 향상을 얻었다.

하지만, gird search는 오직 parameter sapce 안에서 reconstruction error를 최소화하므로, 이는 final perfrmomance를 최소화 하는 것과 동일하지 않다.
따라서, model space에서 quantization parameters를 fine-tuning하기 위해 TGPL 함수를 도입하는 것을 제안했고, 이를 통해 59.40 performance를 얻었다.

최종적으로, adaptive rounding value를 도입하여, free dom degree가 추가되어 final performance gap을 줄이고, 거의 FP 모델과 유사한 performance를 달성했다. (quantized: 60.12 vs FP: 60.32)

4.4 Inference Acceleration

여기선 NVIDIA Jetson AGX Origin 에서 quantization 전후의 CenterPoint 모델의 speed를 비교한다.
이는 실제 자율주행차에서 널리 사용되는 resource-constrained edge GPU platform이다.
quantized model은 inference speed를 3배 높였다.

4.5 Computation Efficiency

LiDAR-PTQ는 기존 PTQ methods에 비해 추가적인 computation과 fine-tuning process가 요구된다. 따라서 time cost가 증가할 것이다.
quantization time은 LIDAR-PTQ의 한계이지만, 다른 PTQ method들과 비교했을 때, LiDAR-PTQ의 time cost는 acceptable하다.
나아가, QAT method에 비해선, 매우 짧다. 예를 들어, CenterPoint-Pillar는 FP 모델과 동일한 성능을 달성하기 위해 WOD dataset에서 94 GPU/hour이 걸리지만
LiDAR-PTQ는 오직 3 GPU/hour가 걸린다. QAT method보다 거의 30배 이상 빠른 것이다.
이는 LiDAR-PTQ가 cost-effective함을 증명한다.

Related Works

PTQ

현존하는 quantization metho는 두 카테고리로 나뉜다.
1) QAT
2) PTQ
QAT는 모든 labeled training data에 access가 필요하기 때문에, data privacy와 security conscer으로 인해 feasible하지 않다.
QUT와 비교해서 PTQ는 사용이 더욱 간단하고, 제한된 unlabeled data로 quantization이 가능하다.

현재, 많은 method들이 2D vision task를 위한 설계가 제시되고 있다.
AdaRound는 layer-wise quadratic unconstrained binary optimization problem으로 rounding task를 formulate하고, 더욱 나은 성능을 달성했다.
BRECQ는 AdaRound를 기반으로, block reconstruction을 활용해서 PTQ의 accuracy를 향상했다.
그 이후, QDrop은 PTQ 도중 activations의 quantzation을 랜덤하게 drop해서 SoTA accruacy를 달성했다.
PD-Quant는 quantization 전후의 global difference를 고려하고, BN layer statists로 activation의 distribution을 adjust하여 overfitting 문제를 막는다.
하지만, 이런 mehtod들은 RGB image들을 위해 설계 되었고, modal difference로 인해 LiDAR point cloud에 transferable하지 않다.

Quantization for 3D Object Detection

QD-BEV(2023)가 baseline BevFormer(2022) 보다 더 작은 size와 faster speed를 달성했다. QAT와 distllation을 multi-camera 3D detection task에 이용했다.

3D LiDAR-based 3D detection에서, 특히 fully convolutional methods를 위해서, PointPillars(2019), FCOS-LIDAR(2022), FastPillars(2023) 등과 같은 quantization solution이 practical requirement를 위해 latency를 speedup했다.

(Stacker et al. 2021)은 2D CNN을 위한 INT 8 quantization을 직접 사용하는 것은 PointPillars에서 significant performance drop을 가져옴을 발견했고,
entropy calibrator보다 더욱 drop이 심했음을 발견했다.

BiPointNet(2021)은 binarization quantization method로, 작은 CAD simulation으로부터 캡처된 point cloud를 기반으로 classification과 segmentation task에 focus한다.

우리가 아는 지식 안에선, self-driving 에서의 large-scasle outdoor LiDAR-based 3D object detection methods를 위해 설계된 quantization solution은 없다.