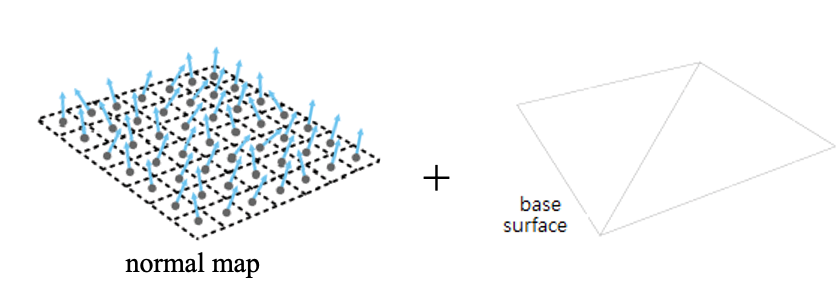
Normal Mapping

• Normal Mapping이란?
  고해상도 mesh 처리에는 많은 시간이 소요된다,
  이를 해결하기 위해 고해상도 mesh의 normal을 미리 계산하고,
  이를 normal map이라고 하는 특수한 texture에 저장한 후,
  runtime에는 저해상도 mesh를 처리하되, normal map으로부터 normal을 읽어서,
  이를 lighting에 사용하는 특수한 texturing 기법.

• normal map을 만드는 방법 중 하나는 height map을 사용하는 것이다.

---

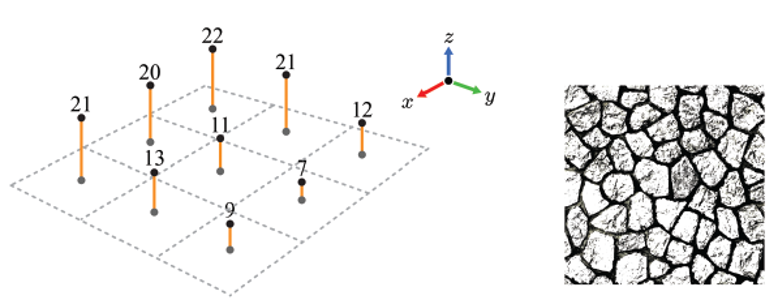
Height map

• hieght map에는
  균일하게 sampling된 $(x,y)$ 좌표에 높이 값 $h$가 저장된다.
  오른쪽 이미지처럼 gray-scale의 이미지로 가시화할 수 있다.
  

• height map은 image texture로부터 반자동으로 생성된다.
  normal map은 height map으로부터 자동으로 생성된다.
  

---

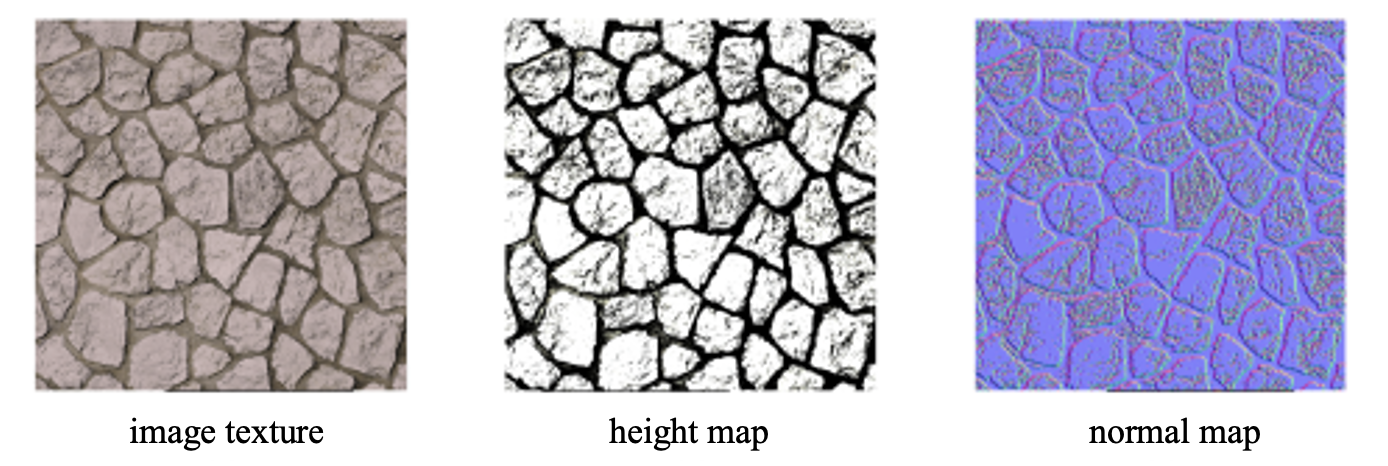
Normal map

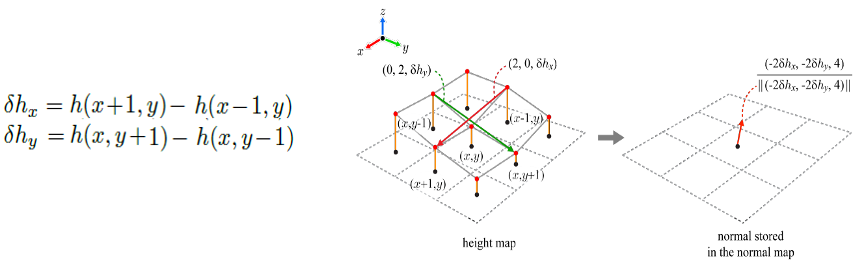
• mesh 표면의 가운데 점인 $(x, y, h(x,y))$의 normal을 계산해보자.
  단, 여기서 $h(x,y)$는 2차원 좌표 $(x,y)$가 주어졌을 때, height 값을 반환하는 함수.

• $(x-1, y, h(x-1, y))$와 $(x+1, y, h(x+1, y))$를 잇는 벡터를 $(2, 0, \delta h_x)$로 표기하고,
  $(x, y-1, h(x, y-1))$와 $(x, y+1, h(x, y+1))$를 잇는 벡터를 $(0, 2, \delta h_x)$로 표기하자.

• $(2, 0, \delta h_x)$와 $(0, 2, \delta h_x)$는 $(x, y, h(x,y))$에서의 tangent vector로 생각할 수 있는데,
  이 둘의 벡터곱 $(-2\delta h_x, -2\delta h_y, 4)$를 $(x, y, h(x,y))$에서의 normal로 취하면 된다.
  이를 정규화한 것이 아래 그림의 가장 오른쪽이다.

• 이 과정을 모두 거치면, 다음과 같은 normal map이 생성되고, image texture와 결합한다.
  

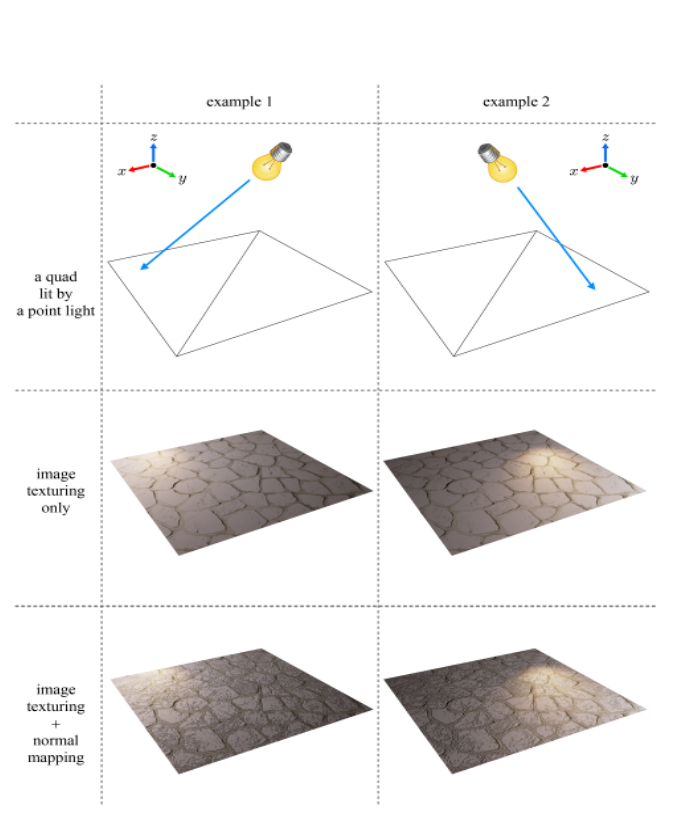
• image texturing만 적용한 사각형과 image texturing + normal mapping을 모두 적용한 사각형을 비교해보면,
  normal mapping을 사용하지 않은 경우, fragment의 normal은 모두 $z$축을 향하는 단위 벡터인 (0, 0, 1)로 고정된다.
  반면, normal mapping을 사용하는 경우, fragment의 normal은 모두 normal map에서 읽어오는데, 이 normal은 (0,0,1)로 고정되지 않은, 조금씩 흔들어 놓은 디테일한 벡터일 것이다.
  따라서 인접한 fragment라고 하더라도, 다른 방향의 normal을 가질 수 있고, 이에 따라 shading 결과가 매우 불규칙하게 되어, 디테일한 영상을 얻게된다.
  

---

Tangent space Normal mapping

• normal mapping을 위해서는, image texturing에서는 불필요했던 한 가지 작업을 더 수행해야 한다.

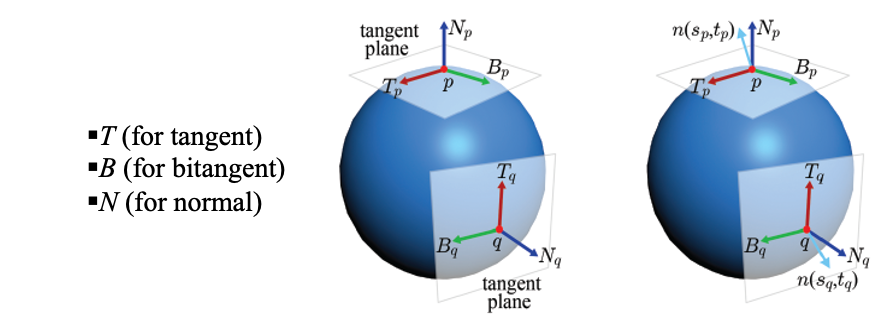
• 물체 표면의 한 점에서의 normal을 $N$이라고 할 때,
  $N$에 수직인 접면(tangent plane)에는
  두 개의 서로 수직인 단위 벡터 $T$와 $B$를 정의할 수 있다.

• 이렇게 한 점에서의 $\{T,B,N\}$은 해당 점과 함께 tanget space를 구성한다.
  표면의 각 점은 자신만의 tangent space를 가진다.

• 왼쪽 그림은 normal mapping을 사용하지 않은 경우, lighting에 $N_p$를 쓰게 되는 경우라고 볼 수 있고,
  오른쪽 그림은 normal mapping을 사용해서, $p$의 texture coordinate $(s_p, t_p)$를 이용해 normal map에서 가져온 normal인 $n(s_p, t_p)$를 사용하는 경우이다.

• 결론적으로, 물체 표면의 어떤 점에서 normal mapping을 적용하든, normal map에서 읽어온 normal은
  바로 그 점의 tangent space에서 정의된 벡터로 보면 된다.
  이런 관점에서 tangent space normal map 이란 용어를 사용한다.

• ${T,B,N}$은 전처리 단계에서 정점별로 계산되고, vertex array에 저장되어 vertex shader로 넘겨진다.
  $T, B, N$은 object space에서 정의된 벡터들이다. vertex shader는 여기에 먼저 world transform을 적용해 world space로 옮긴다.
  그 다음, world space 벡터 $T, B, N$을 행으로 갖는 $3 \times 3$ 회전 행렬을 구성한다.
  이것이 world space 벡터를 tangent space로 변환하는 기저 이전(basis transform) 행렬이다.
  $\\$
  $M_{TBN} \begin{pmatrix} T_x, T_y, T_z \\ B_x, B_y, B_z \\ N_x, N_y, N_z \end{pmatrix}$