[그래픽스] Rasterizer

YEOM JINSEOP·2023년 11월 20일

Computer Graphics

목록 보기

8/14

GPU rendering

GPU는 polygon mesh를 입력으로 받아서,
각각의 3차원 polygon을 스크린에 그려질 2차원 형태로 바꾸고,
이 2차원 polygon 내부를 차지하는 pixel들의 색상을 결정한다.
이 pixel은 color buffer에 기록되는데, 이는 스크린에 나타날 pixel 전체를 저장하는 메모리 공간을 말한다.
color buffer는 주기적으로 스크린에 복사된다.

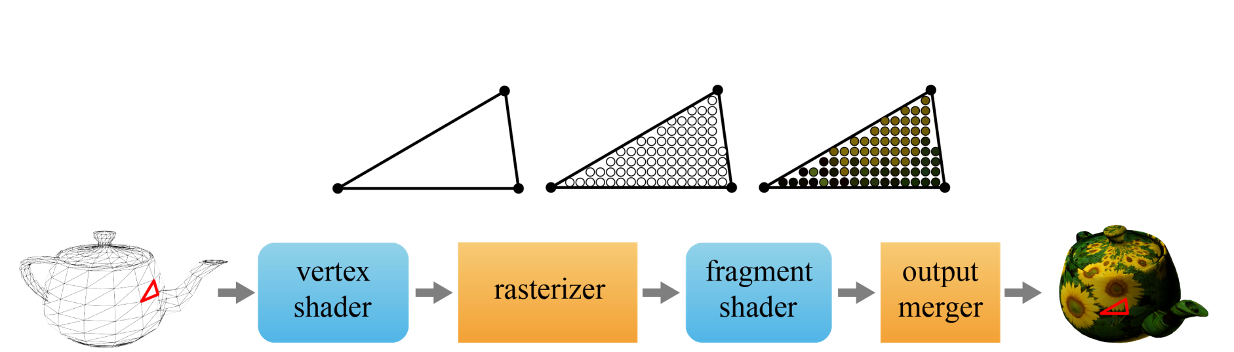
vertex는 program과 동의어다.
GPU rendering을 위해서 vertex shader와 fragment shader 두 가지 프로그램을 작성해야한다.
rasterizer와 output merger는 하드웨어로 고정된 단계로, 정해진 연산을 수행한다.

vertex shader는 vertex array에 저장된 모든 vertx에 대해서 transform을 비롯한 다양한 연산을 수행한다.
rasterizer는 변환된 vertex들로 삼각형들을 조립한 후, 각 삼각형 내부를 차지하는 fragment를 생성한다.
한 fragment는 color buffer의 한 pixel을 갱신하는 데 필요한 데이터를 총칭한다.
예를 들어, 스크린에서 100개의 pixel을 차지하는 삼각형이 있다면,
이 삼각형으로부터 총 100개의 fragment가 만들어진다.
rasterizer가 출력한 fragment는 하나하나 fragment shader로 입력되어,
lighting과 texturing 작업을 거쳐 색상이 결정된다.
output merger는 이러한 fragment와
현재 color buffer에 저장된 pixel 중 하나를 선택하거나 혹은 이들의 색을 결합하여,
color buffer를 갱신한다.

Rasterizer

vertex shader가 출력한 vertex들은 다시 primitive로 다시 조립(assemble)된다.
GPU 파이프라인에서 처리할 기하적인 개체들을 primitive라고 부른다. 삼각형 말고도 line과 point도 독자적인 primitive가 될 수 있다. 하지만, 여기서는 삼각형 primitive만 다룬다.
이 primitive는 스크린에 그려질 형태로 변환된 후, fragment로 분해되는데, 이를 rasterization이라고 부른다.
fragment는 color buffer의 pixel을 갱신하는 데 필요한 데이터를 총칭한다.
vertex들에 저장된 normal과 text coordinate 등은 primitive를 따라 interpolation되어 각 fragment에 할당된다.
이러한 primitive assembly와 rasterization은 GPU 파이프라인의 rasterizer가 담당한다.
shader와 달리 하드웨어도 고정된 단계로,
cliping,
원근 나눗셈(perspective division),
뒷면 제거(back-face culling),
viewport transform,
scan conversion
등의 작업을 수행한다.
Cliping ➡️ Perspective Division ➡️ Back-face culling ➡️ Viewport transform ➡️ Scan Conversion

1. Cliping

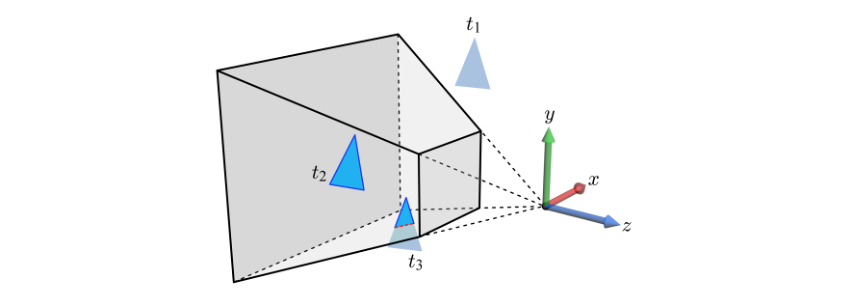
1) 삼각형 $t_1$ 은 view frustum 바깥쪽에 위치하므로 제거된다.
2) 삼각형 $t_2$ 는 view frustum 안쪽에 위치하므로 그대로 둔다.
3) 삼각형 $t_3$ 는 view frustum과 교차하므로, view frustum 바깥에 놓인 부분을 잘라내는 작업이 필요하다.
기존 vertex 일부가 제거되고, 새로운 vertex를 추가해서 새로운 primitive를 만든다.

2. 원근 나눗셈(perspective division)

나눗셈에 사용된 $w$ 좌표는 $- z$ 로, 이는 camera space의 $xy$ 평면으로부터 해당 vertex까지의 수직 거리를 나타내는 양수값이다.
camera로부터 멀리 떨어져 있는 정점은 projection transform 후 $w$ 좌표가 크므로,
$w$ 로 나누는 연산은 머리 떨어진 물체를 작게 만든다. ➡️ 원근법 구현

아래 예시에서 $M_{proj}$ 에 의해 변환된 vertex의 $w$ 좌표는 $-z$ 가 된다.
projection transform을 camera space의 한 점 (x, y, z, 1)에 적용한 예시

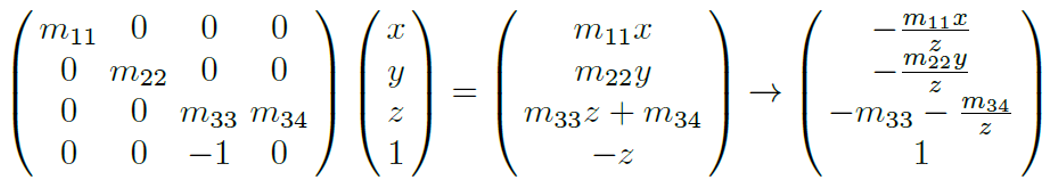
3. 뒷면 제거(back-face culling),

개념적인 뒷면 제거

가상 camera를 등지고 있는 polygon을 back-face라고 부른다.
이는 camera에 보이지 않으므로 제거될 것이다.
반면, camera를 향하는 polygon은 front-face라고 부르는데,
이는 보존되어 rasterizer의 다음 단계로 넘어갈 것이다.

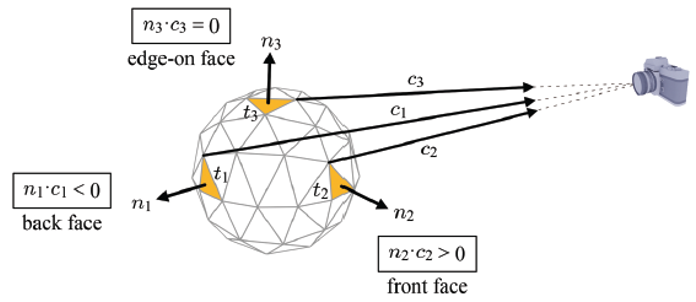
카메라(EYE)가 삼각형 normal이 가리키는 방향의 반대쪽에 존재한다면 이 삼각형은 back-face이다. ➡️ $t_1$
이를 구분하기 위해선 삼각형의 vertex와 camera를 연결하는 벡터가 필요하다.
이를 $c_i$ 라 하고, 삼각형 normal $n_i$ 와 $c_i$ 의 내적을 계산해서 판단한다.

뒷면 제거의 실제 구현

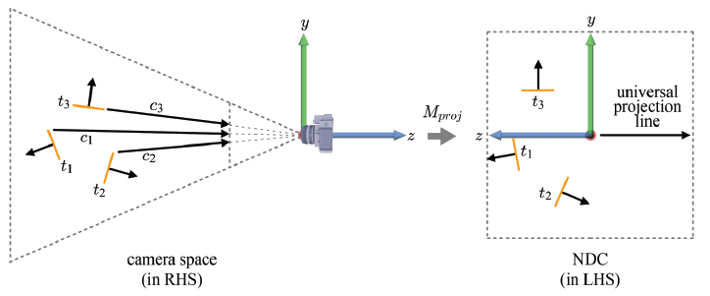
projection transform 이후에는 모든 $c_i$ 가 $z$ 축과 나란해진다. (단일한 투영선과 일치됨)
projectoin transform이 적용된 구가 주어졌을 때, 아래 예시처럼 이 구의 삼각형들을 단일한 투영선을 따라 $xy$ 평면으로 투영해보자.

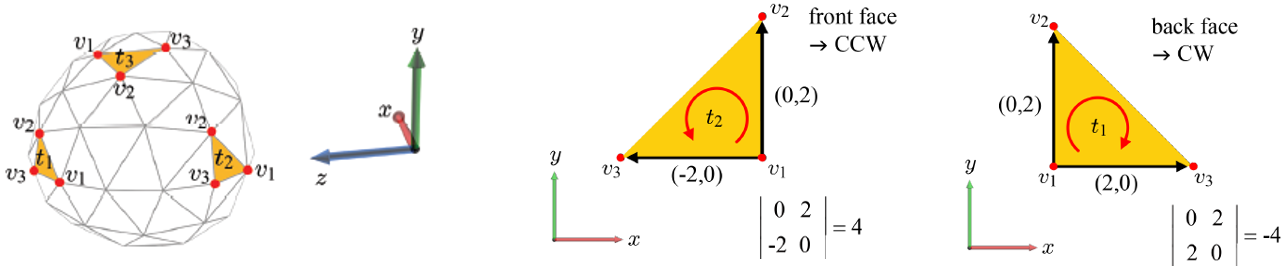
3차원 공간에서는 $t_1$ 을 포함한 모든 삼각형들의 vertex들이 반시계 방향으로 정렬되었었다.
그런데, back-face인 삼각형 $t_1$ 을 투영한 결과는 vertex들이 시계 방향으로 정렬되어 있다.
반면, front-face인 삼각형 $t_2$ 를 투영한 결과는 vertex들이 반시계 방향으로 정렬되어 있다.
이러한 성질을 이용해서,
2차원으로 투영된 vertex가 시계 방향으로 정렬되면 back-face로 판정하고,
반시계 방향으로 정렬되면 front-face로 판정한다.
삼각형의 vertex들이 시계 방향 혹은 반시계 방향으로 정렬되어 있는지는 행렬식(determinant)를 사용해 판정한다.
2차원으로 투영된 삼각형 $<v_1, v_2, v_3>$ 를 생각해보자. 각 정정 $v_i$ 는 $(x_i, y_i)$ 좌표를 가진다.
우선 $v_1$ 과 $v_2$ 를 잇는 벡터 $(x_2 - x_1, y_2 - y_1)$ ,
그리고 $v_1$ 과 $v_3$ 를 잇는 벡터 $(x_3 - x_1, y_3 - y_1)$ 을 계산한 후, 다음과 같은 행렬식을 이용한다.
$\\$
$\begin{vmatrix} (x_2-x_1) & (y_2 - y_1) \\ (x_3-x_1) & (y_3 - y_1) \end{vmatrix} = (x_2-x_1)(y_3 - y_1) - (x_3-x_1)(y_3-y_1)$

이 행렬식의 값이 음수라면 시계방향, 즉 back-face이고
양수이면 반시계방향, 즉 front-face가 된다.
만약 0이라면, 변만 보이는 삼각형을 의미한다.

4. Viewport Transform

컴퓨터 스크린 위의 윈도우는 그 자신의 좌표계를 가지는데,
이를 window space 혹은 screen space라고 부른다.
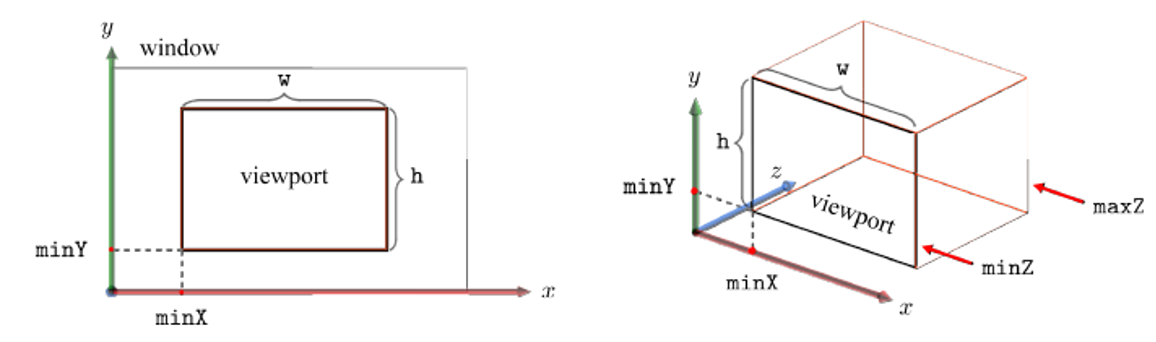
위 그림과 같이 window의 왼쪽 아래 모퉁이에 원점을 가진다.
한편, clip space 정육면체 view volume 안의 내용이 최종적으로 그려질 스크린 영역을 viewport라고 한다.
window에서 viewport의 범위는 glViewport에 의해 정의된다.
goViewport는 다음 parameter를 사용한다.
1) minX와 minY: viewport 왼쪽 아래 모퉁이의 screen space 좌표
2) w, h: viewport의 너비와 높이
viewport의 aspect ratio는 w/h가 되는데, 이는 view frustum의 parameter인 aspect와 동일하게 설정하는게 좋다.
clip space로 표현된 2 $\times$ 2 $\times$ 2 크기의 view volume은 viewport로 변환될 때,
scaling과 translation을 결합한 행렬에 의해 변환된다.
viewport transform =
$\\$
$\begin{pmatrix} \frac{w}{2} & 0 & 0 & minX + \frac{w}{2}\\ 0 & \frac{h}{2} & 0 & minY + \frac{h}{2}\\ 0 & 0 & \frac{maxZ-minZ}{2} & \frac{maxZ+minZ}{2} \\ 0 & 0 & 0 & 1 \end{pmatrix}$
viewport transform은 2 $\times$ 2 $\times$ 2 크기의 view volume 안에 있는 모든 vertex에 적용된다.

5. Scan Conversion

viewport transform은 모든 삼각형들을 screen space로 옮긴다.
그 다음, scan conversion이 수행된다.
scan conversion: 삼각형 내부를 채우는 fragment를 생성한다.
fragment에는 normal과 texture coordinates가 저장되어 있음.
구체적으로는, 개별 삼각형이 차지하는 screen space의 pixel 위치를 결정하고,
삼각형의 vertex별 attriute를 interpolation하여 이를 각 pixel 위치에 할당한다.
scan conversion에서는 $xy$ 좌표만 사용한다. 따라서 아래와 같이 2차원 viewport를 사용해 설명한다.
이를 확대해 본 것이 가장 오른쪽 그림의 삼각형이고, 이 내부에는 18개의 pixel이 있다.
이들 각각의 pixel 위치에 vertex별 attribute가 interpolation되어 할당될 것이다.
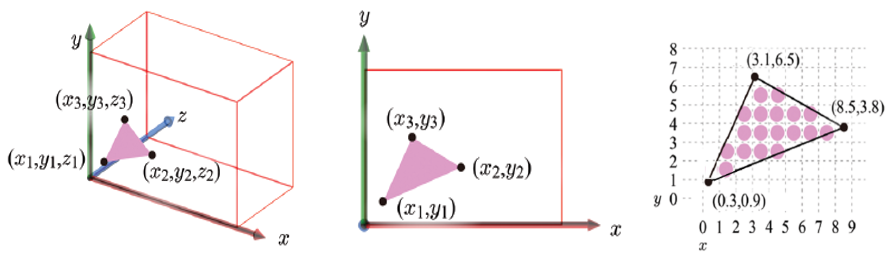
vertex별 attribute는 우선 삼각형의 변을 따라 linear interpolation된다.
interpolation을 위해서는 몇 가지 기울기가 필요하다.
1) $\Delta{attribute}/\Delta{y}:$ 수직 거리 $y$ 의 변화에 따른 $R$ 의 변화율
2) $\Delta{attribute}/\Delta{x}:$ 수평 거리 $x$ 의 변화에 따른 $R$ 의 변화율
수평 방향으로 이어진 스크린 pixel들을 scan line이라고 부른다.
이 scan line을 따라 attributeem들을 interpolation한다.
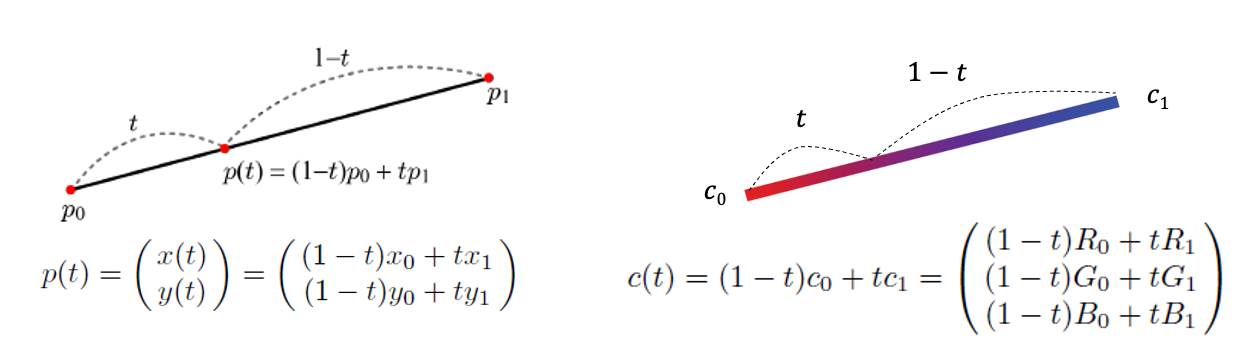
scan conversion은 두 단계로, 먼저 변을 따라 진행되고, 그 다음에는 scan line에 따라 수행된다.
이를 겹선형보간(binliear interpoltation)이라고 한다.