-
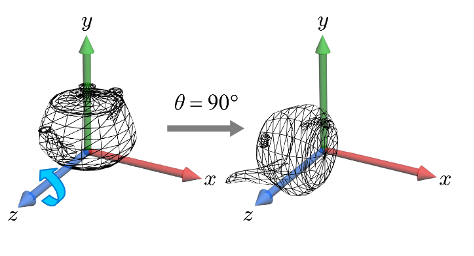
2D rotation에서는 회전 중심(center of rotation)을 필요로 하는데 반해,
3D rotation은 회전축(axis of rotation)을 필요로 한다.
-
Rz(θ): z 축을 중심으로 θ 만큼 회전 ➡️ x,y 좌표가 바뀜.
⎝⎜⎛x′y′z′⎠⎟⎞=⎝⎜⎛cosθsinθ0−sinθcosθ0001⎠⎟⎞⎝⎜⎛xyz⎠⎟⎞
-
Rx(θ): x 축을 중심으로 θ 만큼 회전 ➡️ y,z 좌표가 바뀜.
⎝⎜⎛x′y′z′⎠⎟⎞=⎝⎜⎛1000cosθsinθ0−sinθcosθ⎠⎟⎞⎝⎜⎛xyz⎠⎟⎞
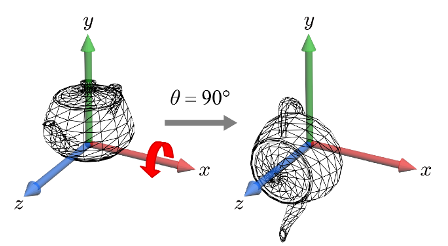
-
Ry(θ): y 축을 중심으로 θ 만큼 회전 ➡️ x,z 좌표가 바뀜.
⎝⎜⎛x′y′z′⎠⎟⎞=⎝⎜⎛cosθ0−sinθ010sinθ0cosθ⎠⎟⎞⎝⎜⎛xyz⎠⎟⎞
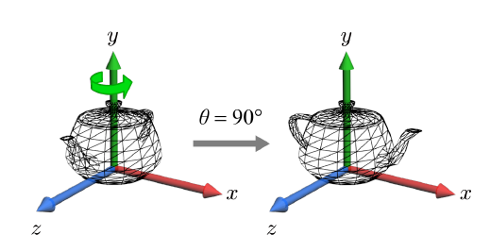
-
동차 좌표(homogeneous coordinate)를 다루기 위해서는 3 × 3 행렬 형태를 4 × 4 행렬 형태로 변경한다.
Rz(θ)=⎝⎜⎜⎜⎛x′y′z′1⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛cosθsinθ00−sinθcosθ0000100001⎠⎟⎟⎟⎞⎝⎜⎜⎜⎛xyz1⎠⎟⎟⎟⎞
Rx(θ)=⎝⎜⎜⎜⎛x′y′z′1⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛10000cosθsinθ00−sinθcosθ00001⎠⎟⎟⎟⎞⎝⎜⎜⎜⎛xyz1⎠⎟⎟⎟⎞
Ry(θ)=⎝⎜⎜⎜⎛x′y′z1⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛cosθ0−sinθ00100sinθ0cosθ00001⎠⎟⎟⎟⎞⎝⎜⎜⎜⎛xyz1⎠⎟⎟⎟⎞
-
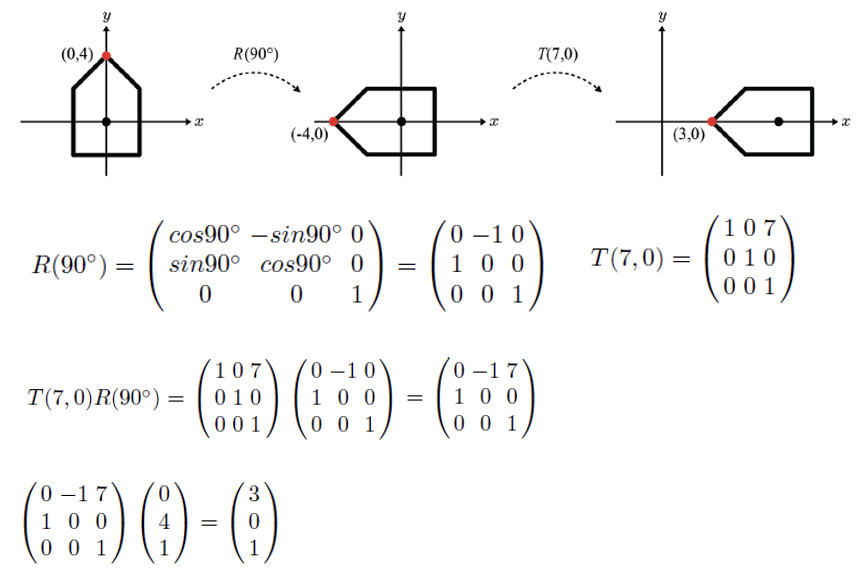
T의 역변환을 T−1 이라고 표기하고, 실제로 T의 역행렬이다.
-
이동(Translation)의 역변환
T=⎝⎜⎜⎜⎛100001000010dxdydz1⎠⎟⎟⎟⎞, T−1=⎝⎜⎜⎜⎛100001000010−dx−dy−dz1⎠⎟⎟⎟⎞
-
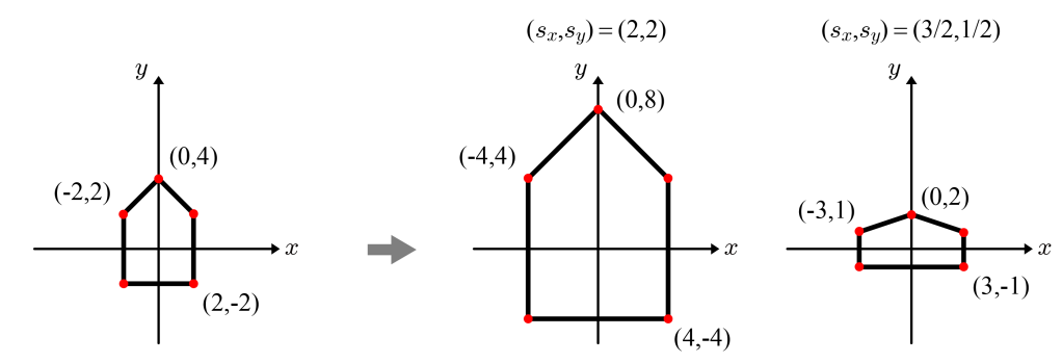
Scaling의 역변환
S=⎝⎜⎜⎜⎛sx0000sy0000sz00001⎠⎟⎟⎟⎞,S−1=⎝⎜⎜⎜⎛1/sx00001/sy00001/sz00001⎠⎟⎟⎟⎞
-
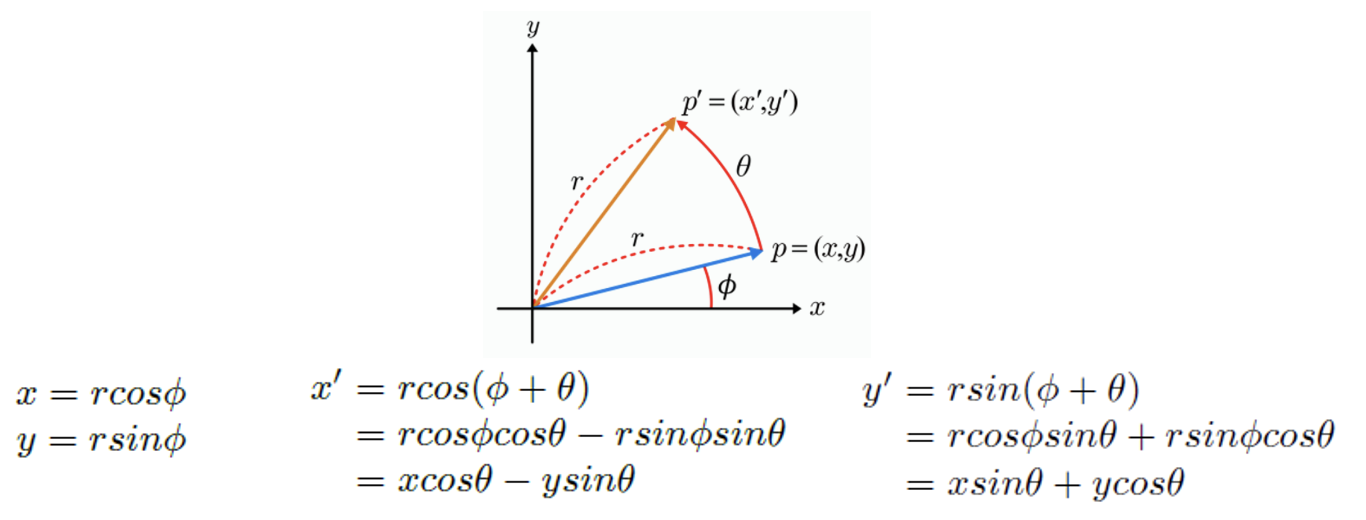
Rotation의 역변환
R=⎝⎜⎛uxuyuzvxvyvznxnynz⎠⎟⎞,RT=⎝⎜⎛uxvxnxuyvynyuzvznz⎠⎟⎞
[식 유도하기 ]
object space의 기저 {u,v,n}이 직교 적교 성질을 가지므로,
하나의 기저 벡터가 자신과 내적되었을 때 그 결과는 1이다. ➡️ u⋅u=v⋅v=n⋅n=1
반면, 서로 다른 기저 벡터간 내적은 0이다. ➡️ u⋅v=v⋅n=n⋅u=0
이를 이용해서, rotation 행렬 R과 그 전치행렬 RT의 곱을 정리하면 다음과 같다.
RTR=⎝⎜⎛uxvxnxuyvynyuzvznz⎠⎟⎞⎝⎜⎛uxuyuzvxvyvznxnynz⎠⎟⎞