[LGaimers] 인과 추론

Part 1. 인과성에 대한 소개 및 인과성 추론을 위한 기본 개념

casual discovery

• 데이터로부터 인과효과와 인과관계를 계산
  casual descision making
• 효율적으로 환경과 인터랙션 하는 것을 연구
  Bayesian Network
• 확률적 그래피컬 모델에 대한 기본적 지식

Causality(인과성)

• 하나의 어떤 무엇인가가 다른 무엇을 생성함에 있어 영향을 미치는 것
• 부분적인 관계
• 운동을 많이하면 비만 감소, 버스를 놓쳐서 지각을 했다 (인과적 관계)
• 관련이 있다, 연관이 있다 -> 상관성의 정보 제시

법칙

• 현상의 본질적인 구조를 명확하게 하는 것
  Cause and Effect
• 원인과 결과의 메커니즘을 기술한 것

인공지능

• 소프트웨어, 로봇 등 어떤 에이전트가 목표를 성취하기 위해 합리적인 액션을 취하는 것
  강화학습
• 주어진 상황에서 어떤 행동을 취할지 학습
• 환경에 변화를 주어 원하는 상태로 변화시키는 인과관계로 해석 가능
  기계학습
• 데이터의 상관성을 학습

인과 계층

• 첫번째, 가장 기본적인 관측 계층, 시스템을 구성하는 변수들의 상관성을 파악, 비교할 수 있음
• 두 번째, 실험 계층, 연구하고자 하는 시스템을 중재함으로써 나오는 결과에 집중 , ex 아스피린을 두 그룹에 무작위로 먹게함
• 세 번째, 관측 값과 실험에 의한 값을 동시에 고려하는 반사실적 계층

Simpson's Paradox

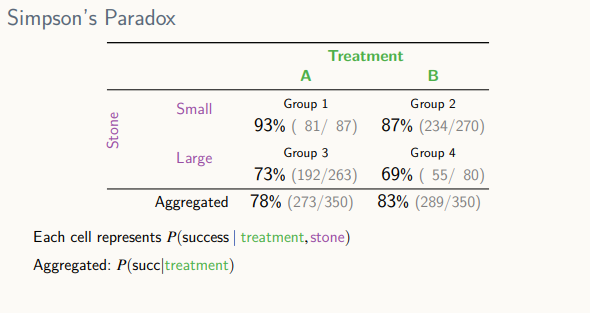
• 결석의 상태와 처방에 따라 환자의 나중 건강 상태가 달라짐

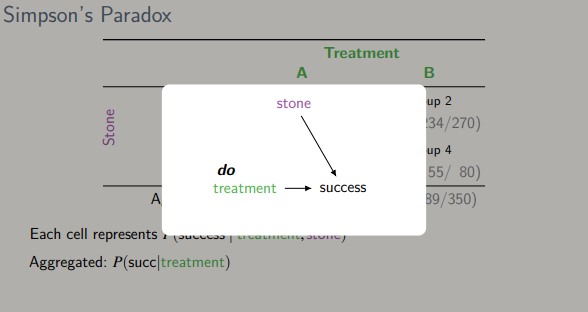
• 처방은 더 이상 신장 결석의 사이즈에 무관

• 가상의 무작위 실험 -> 인과 효과를 계산할 수 있음

• 인과적인 분석을 하기 위해서는 주어진 데이터뿐만 아니라 각 변수들이 가지는 인과적 관계에 대한 이해가 필요

• 변수들 간의 인과적 관계가 그림과 다르다면 인과 효과의 결과가 다르게 도출 될 수 있음

데이터 분석 시 고려해야할 사항
1) 주어진 데이터가 상관성을 지니고 있는지, 인과성을 지니고 있는지
2) 우리가 알고자하는 질문이 단순히 조건부 확률같은 상관성에 관한 것인지, 인과성에 관한 것인지

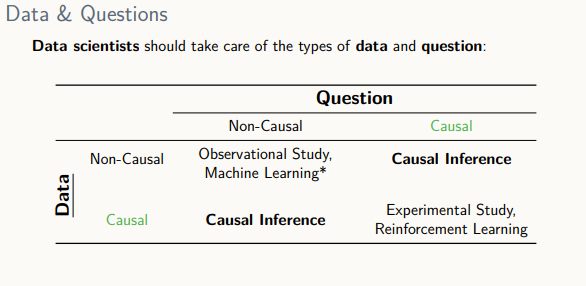
인과 추론

• 인과적인 통찰을 이용하여 하는 그 모든 추론, Casual Inference라고 넓게 정의

계층을 넘나드는 추론 (관층 계층 <-> 실험 계층)

• 인과 추론은 알 수 없는 실험 결과를 관측 데이터와 연결 , 이 두 가지를 연결하려면 블랙박스에 대한 형식적인 수학적 이해가 필요

관측 가능한 변수 V를 생성

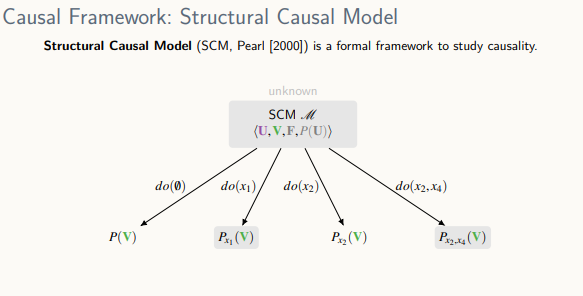
• 이 모델을 기반으로 어떠한 중재도 하지 않을 경우 관측 가능한 모든 변수들에 대한 관측 분포를 볼 수 있는 것, 임의의 변수를 중재하게 된다면 실험에 대한 결과 분포가 나오게 됨

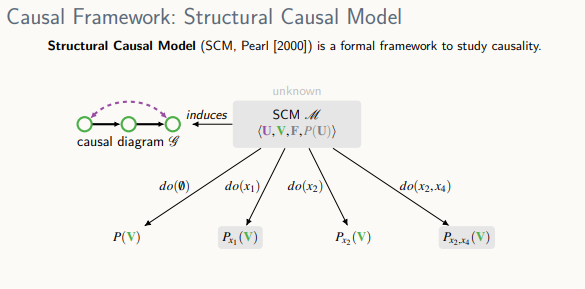
casual diagram : 전문가들의 지식이나 상식 또는 가정에 의해 만들어지는 것

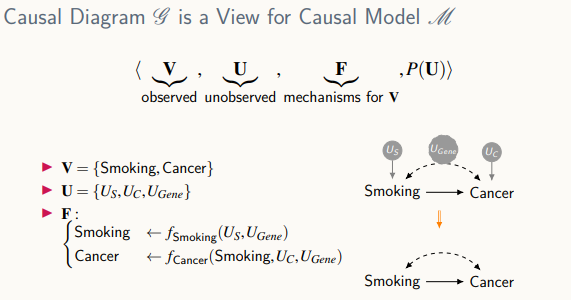
Structual Causal Model(SCM)

• U는 관측되지 않은 변수, V는 관측 가능한 변수
  

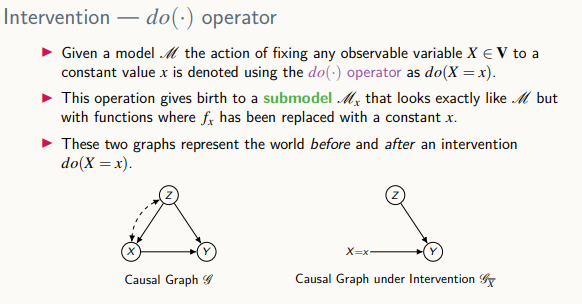
중재

Causal Effects (인과 효과)

• 임의의 변수 집합 X가 있고 이 집합 X가 고정되어 있을 때 관심을 가지고 보는 변수 Y가 특정값을 가지는 확률은 어떻게 될 것인가
  

인과추론 할 때 데이터는 상관성만을 갖고 Causal diagram을 가정을 통해 갖게 됨. causal effect를 계산하기 위해서는 causal diagram에 있는 모든 정보를 이용해 인과 효과를 계산해야 함 - > 가장 많이 사용하는 정보 : 변수들 간의 인과관계, 인과관계 통해 그래프에서 나타나는 조건부 독립성

1,2의 경우 conditional dependency 유지
그래프에서 두 변수간의 패스가 존재하는지, 또 그 패스가 열려있는지 닫혀있는지 판단하여 조건부 독립성을 이끌어냄

요약)

SCM은 인과추론을 위한 수학적 프레임워크를 제공
SCM은 관측, 실험, 반사실적 분포 계층을 포함함
모델을 알 수 없기 때문의 모델의 부분적인 정보로써 causal diagram을 가정
causal diagram은 가정에 의해 상식, 전문가의 지식 등에 의해 생성
모델을 통해 수학적으로 중재를 정의 , 원래 모델이 아닌 submodel이 생성됨, 화살표가 다 삭제된 그래프
우리가 결국 알고싶은 causal effect를 위와 같이 정의

Part 2. 인과추론 수행을 위한 기본 방법론 제시

인과효과가 어떻게 그래프를 통해 특정될 수 있는가

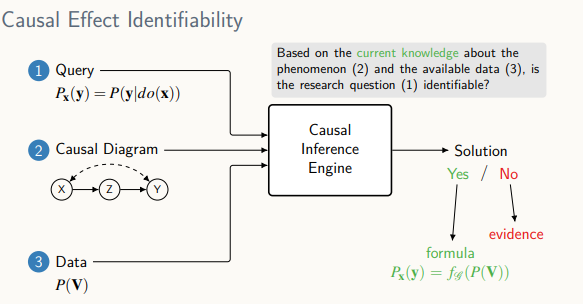
인과 추론 알고리즘 - 인과 추론의 목적

• Z변수 : X와 Y에 서로 영향을 미치는 교란 변수
• W변수: X와 Y 중간에 있는 변수, mediator
• 결합 확률을 식으로 decompose 해놓고 거기에 x가 나오는 확률을 1로 바꾸면 중재 때의 확률 분포가 어떻게 될지 알 수 있게 됨
  
• 식을 전개한 뒤 중재하고 있는 변수와 관련된 조건부 확률을 제거하여 인과효과 계산 -> 그래프들의 모든 변수들이 관측 가능해야함
  
• Adjustment Formular : 인과효과를 구하는 식
• Back-door: 더 일반화

Back-door Criterion

• 뒷문을 제거하기 위해 그래프에서 앞으로 가는 Edge를 제거
• 직접 연결 관계: 직접 연결되어 있기 때문에 나타나는 상관성
• 교란 변수에 의한 연결 관계: z->x->y
• x와 y 사이의 상관성만을 보고 싶기 때문에 교란을 없애는 것이 목적, 뒷문 z를 자른다는 의미
  
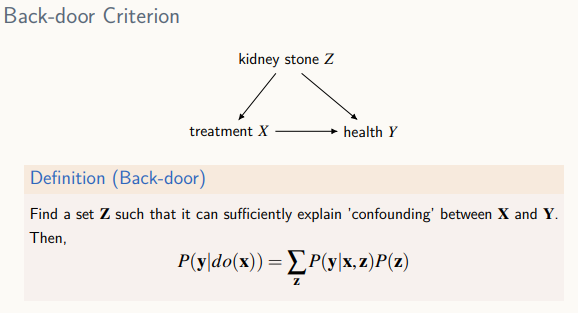
  조건
• Z가 X 이후에 X, X의 영향을 받으면 안됨, not descendent
• X에서 Y로 가는 길 중 뒤로 가는 길을 다 막을 수 있어야 O-> back door formula 가능
  
  - Back-door Criterion =Sound, not complete, 모든 formular를 찾는 것을 보장하진 X -> 이러한 문제를 해결한 것이 Do-calculus

Do-calculus

• Sound&Complete -> 모든 formular에 대해 인과효과를 계산하는 식을 Do-calculus와 공리를 이용해 이끌어낼 수 있음 but it has no algorithmic insight
• 여러 가지 다른 중재 조건에서 나오는 확률들끼리 서로 연결고리를 만들어주고 서로 다른 중재로 어떤 확률 분포를 바꿔주는 역할

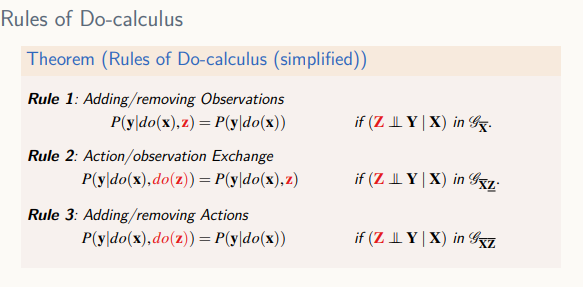
• 첫번째 룰 : 관찰에 대한 것이 추가되거나 삭제될 수 있다 -> 조건부 독립
• 두번째 룰 : Action 과 Observation을 바꿀 수 있다
  X에 대해서는 들어가는 edge를 지우고 Z에 대해서는 나가는 edge들을 지운 그래프에서 조건부 독립을 d-seperation을 통해 확인
• 세번째 룰: Action이 추가되거나 제거될 수 있다, 즉 Action을 취하는 것이 아무런 영향X

어떤 규칙에 의해 조건부 독립 만족
-> 확률을 다른 확률로 변경시킬 수 있다

Part 3. 인과추론의 다양한 연구 방향 제시

주어져있는 도메인-> 관측 데이터 -> 인과 효과
여러 종류의 데이터가 있다면 한 번에 활용해 원하는 인과효과를 계산하면 더 낫지 않을까?

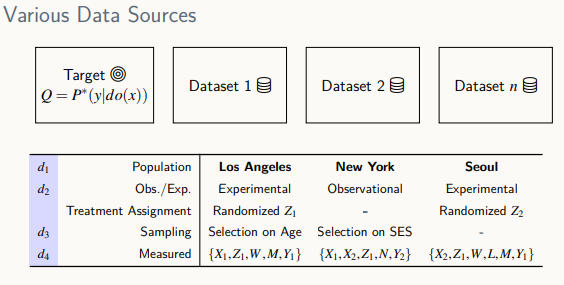
+) SES: 사회 경제적인 사람들의 상태에 따라 데이터 수집

• 데이터들은 다양한 특성을 가짐
  
• 관측 데이터로 인과효과를 얻을 수 없을 경우, 실험 데이터로 원하는 인과효과를 도출
  
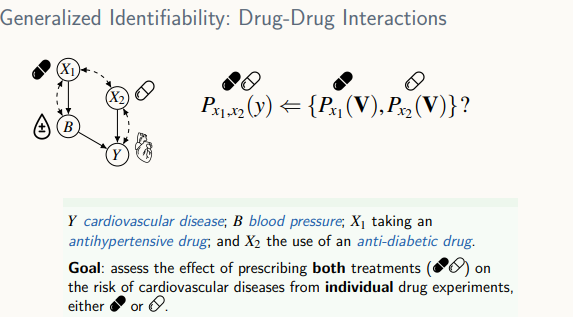
• 각각의 약에 대해 실험한 데이터가 있을 때 두 약을 혼용한 경우 어떤 효과가 날지 알고 싶은 것
  
  
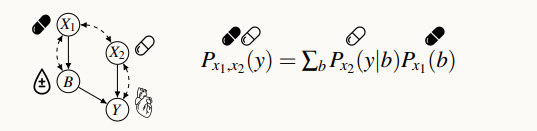
  General Identifiability
• 여러 데이터(중재, 관측 등) 가 한 도메인에 주어져 있을 때 그것을 활용해 원하는 인과효과를 계산하는 것

기계학습에서의 가정

• training dataset과 test dataset이 같은 환경에서 만들어진 것이라 가정 (하나의 도메인)

Transportability

• 주어져 있는 데이터의 소스와 우리가 인과 효과를 계산하고자 하는 타겟이 서로 다른 도메인일 때의 인과 추론을 다룸

• target domain과 source domain 사이 차이를 명시하여 인과효과를 구함

• selection diagram을 이용하여 효과적으로 계산

• transportability 또한 do-calculus를 이용

• 단순 인과 추론이 아닌 통계적 추론
  

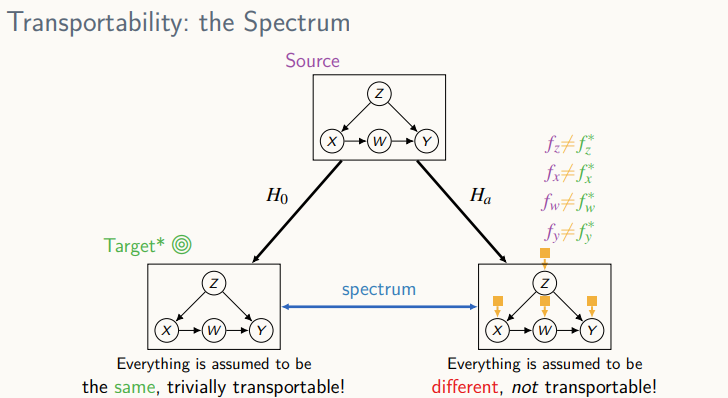
• source와 target사이 공통점이 존재하지만 부분적으로 어떤 변수에 대해서는 다를 수 있다는 것을 인정 -> transportability의 목적
  

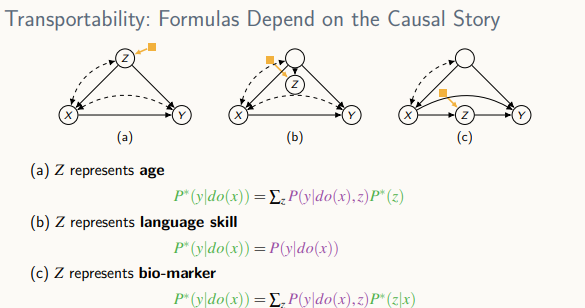
• 실험 데이터를 절대적으로 받아들이지 X

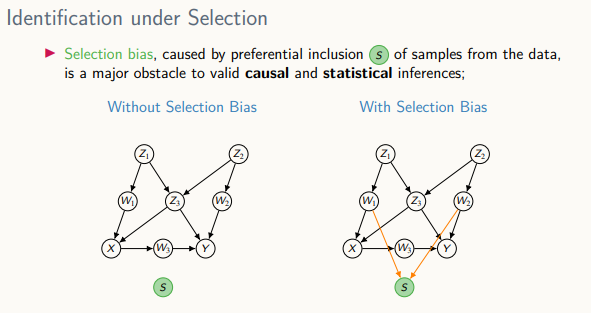
데이터 샘플링 과정에서 선택 편향이 생긴 경우
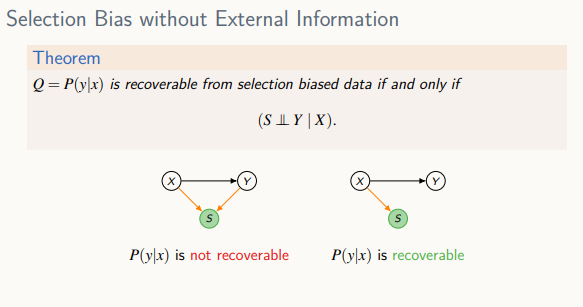
선택 편향

• 데이터의 샘플이 선택적으로 포함되는 경우 발생되는 편향
  
  
  

누락 데이터



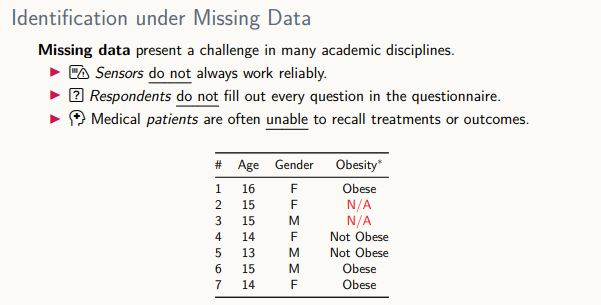
새로운 두 변수를 추가
1) 실제 학생의 비만도
2) 비만도가 누락되는 메커니즘

누락되는 원인
1) Missing Completely At Random 완전 무작위
2) Missing at Random 메커니즘이 누락된 변수와 어떤 조건부 독립이 성립
3) Missing Not At Random 랜덤하지 않은 누락

누락된 정보가 있는 줄들을 삭제, 빈 값들을 채우는 알고리즘들
MCAR,MAR에 부분적으로 동작하지만 MNAR에는 동작하지 않음

요약
1) General Identification : 다양한 실험조건의 데이터를 어떻게 활용할 것인가
2) Transportability: 서로 다른 데이터 소스가 있을 때 소스의 차이를 명시
3) Selection variable: 선택편향이 있는 경우 selection variable 을 추가
4) Missingness : 누락데이터