📊 통계 라이브세션 3회차 : 다양한 가설검정 방법
1. T검정 (t-test)
1개 또는 2개의 집단 평균(정규기반 추정량)을 비교할 때 사용하는 대표적인 모수 검정법
✅ T검정의 전제
- 모수 검정에 속함
- 보통 정규분포에서 나온 데이터라는 전제를 가짐 →
정규성
- 보통 정규분포에서 나온 데이터라는 전제를 가짐 →
- 독립된 두 집단의 평균을 비교하는 경우
→ 분산이 같다는등분산성을 가정하는 경우가 많음
🔎 T-검정의 종류
- 독립표본 T검정
→ 서로 독립된 두 집단의 평균 차이 비교
2. 정규성 & 등분산성
🧪 정규성 (Normality)
- 표본이 정규분포를 따르는 모집단에서 나왔다고 가정
🧪 등분산성 (Homogeneity of Variance)
- 두 집단의 분산이 동일하다고 가정
📈 정규성 검정 관련 메모
표본이 많으면 정규성은 사실상 크게 신경 쓰지 않아도 됨

❓ 정규성과 등분산성, 꼭 검정해야 할까?
-
표본수가 충분히 크면
→ 중심극한정리에 따라 정규성 가정이 완화됨 -
실제로 AB 테스트에서는 거의 정규성을 따지지 않음
-
하지만 소표본일수록 정규성과 등분산성 확인이 매우 중요
- 정규성 위반 → 비모수 검정 사용
- 등분산성 위반 → Welch t 검정 사용
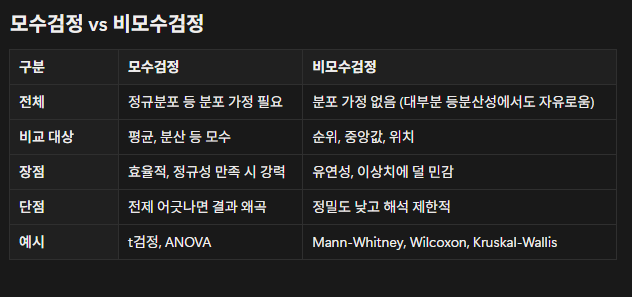
3. 비모수 검정 (Non-parametric test)
모집단의 분포를 전제로 하지 않는 검정 방법
→ 정규분포를 가정하지 않아도 사용할 수 있음
현실의 데이터는 정규분포를 가정할 수 없는 경우가 많고, 이럴 땐
모수(평균, 분산)를 비교하는 것을 신뢰할 수 없음.
🔹 비모수 검정을 고려해야 하는 경우
- 극단값(이상치)이 많은 경우
- 좌우 비대칭 분포인 경우
- 표본 수가 너무 작은 경우
4. 분산분석 (ANOVA : Analysis of Variance)
3개 이상 집단의 평균 차이를 비교하는 검정방법
(t검정의 확장 형태)
⚠️ 왜 t검정을 반복해서 쓰면 안 될까?
3개 이상의 집단에서 평균 비교를 위해 t검정을 계속 쓰면:
- 검정이 반복될수록 1종 오류(α, 잘못된 기각) 누적
- 그래서 한 번의 검정으로 모든 집단 간 평균 차이 유무를 판단하는 방법이 필요 → ANOVA
🧠 ANOVA의 원리
분산을 나눠서 비교함으로써 평균 차이를 판단
- 집단 간 변동(Between-group variance) 이 크고
집단 내 변동(Within-group variance) 이 작다면
→ 집단 간 평균에 차이가 있다고 판단
💡 ANOVA 예시
- 예를 들어, 3가지 랜딩페이지 디자인(A/B/C) 를 만들어서
- A그룹, B그룹, C그룹 각각에게 랜덤 노출
- 각 그룹의 평균 전환율(가입률) 을 비교하고 싶다면?
- 이때
→ A vs B, A vs C, B vs C를 t검정으로 따로따로 돌리면
→ 검정 횟수만큼 1종 오류가 누적됨 - 대신 한 번의 ANOVA로
“세 그룹의 평균 전환율이 전부 같은가?”
를 통합해서 검정한다.
🎯 ANOVA 가설 설정
- 귀무가설(H₀) : 모든 집단의 평균이 같다
- 대립가설(H₁) : 적어도 하나의 집단 평균은 다르다
ANOVA는
“어느 집단끼리 다른지”는 알려주지 않고
“차이가 존재하는지 여부”만 알려줌
→ 그래서 유의미한 차이가 나면, 사후검정(Post-hoc test) 이 필요함
5. 비율 / 빈도 중심 가설검정
범주형 데이터를 숫자로 표현하면 비율 또는 빈도가 된다
→ 이때 이항분포 / 포아송분포가 등장!
🧩 범주형 변수란?
수치가 아닌 범주(label) 로 구분되는 변수
- 명목형(Nominal)
- 성별, 지역, 혈액형처럼 순서나 크기 개념이 없는 변수
- 이항형(Binary)
- 결과가 딱 2개뿐인 명목형
- 예시:
구매/비구매,성공/실패,클릭/비클릭
- 순서형(Ordinal)
- 만족도(
상/중/하), 학점(A/B/C)처럼
순서는 있지만 간격이 일정하지 않은 변수
- 만족도(
🔧 범주형 데이터를 분석하는 2가지 방식
-
숫자로 변환해 비율/빈도를 비교하는 방식
(이산형 형태 분석)- 이항형의 경우
0과1로 변환 - → 이항분포 기반 분석
- 이항형의 경우
-
범주 자체의 분포나 관계를 비교하는 방식
(범주형 관계 검정)
6. z검정 (두 비율 검정, Two-proportion z-test)
두 개 집단의 비율 차이가 통계적으로 유의한지 비교할 때 사용
→ 실무 AB테스트에서 거의 항상 쓰는 기본 검정
예시 느낌:
- A버전 버튼 클릭률 = 5%
- B버전 버튼 클릭률 = 7%
- “이 2%p 차이가 우연인지, 아니면 진짜로 B가 더 좋은지 알고 싶다”
→ 이때 두 비율 z검정 사용
7. 범주형 변수 간 관계
우리가 자주 던지는 질문들 👇
- 성별에 따라 구매 여부가 달라질까?
- 유입 채널에 따라 회원가입률이 다를까?
- 기기 OS(iOS/Android) 에 따라 전환율 패턴이 다를까?
이런 질문들은
→ “범주형 변수들끼리 서로 관련이 있는지”를 보는 문제
8. 카이제곱(χ²) 검정
두 개의 범주형 변수의 관계 또는 분포 차이를 판단하는 대표적인 방법
📌 카이제곱 독립성 검정
두 범주형 변수 간에 관련이 있는지(독립인지) 를 검정할 때 사용
✅ 사용 조건
- 교차표(Contingency table) 로 표현 가능한 두 범주형 변수
- 예:
- 행: 성별(남/여)
- 열: 구매여부(구매/비구매)
- 예:
- 행과 열 변수 간 관계가 있는지를 본다
- 예: “성별에 따라 구매 비율이 다른가?”
9. 파이썬 코드 구현
scipy.stats:scipy라이브러리 내에서
통계검정, 확률분포, 샘플링에 유용한 모듈
from scipy import stats
# 예시 1) 독립표본 t검정
stats.ttest_ind(group_a, group_b, equal_var=True) # 등분산 가정일 때
stats.ttest_ind(group_a, group_b, equal_var=False) # Welch t-test
# 예시 2) 두 비율 z검정 (직접 구현 예시)
# 클릭수: click_a, click_b
# 노출수: n_a, n_b
# 예시 3) 카이제곱 독립성 검정
from scipy.stats import chi2_contingency
chi2, p, dof, expected = chi2_contingency(contingency_table)