TIL_351208 본캠프 36일차
모집단과 표본
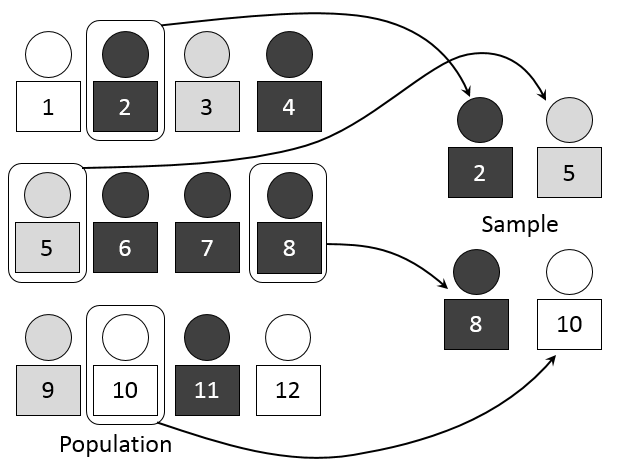
모집단 : 관심의 대상이 되는 전체집단 EX) 한 국가의 모든 성인
표본 : 모집단에서 추출한 일부 EX) 그 국가의 성인 중 일부를 조사
-
표본을 사용하는 이유
1) 현실적인 제약 : 비용과 시간, 접근성
2) 대표성 : 잘 설계된 표본은 모집단의 특성을 반영(무작위 추출)
3) 데이터 관리 : 처리 및 품질관리 용이성
4) 모델 검증용이
✅ 파이썬 실습
import numpy as np
import matplotlib.pyplot as plt
#모집단생성
population = np.random.normal(170, 10, 10000) ->평균 170, 편차10, 1000개의 데이터
#표본추출
sample = np.random.choice(population, 100) -> 무작위로(랜덤하게) 100개
plt.hist(population, bins=50, alpha=0.5, label='population', color='blue')
plt.hist(sample, bins=50, alpha=0.5, label='sample', color='red')
plt.legend()
plt.title('population and sample distribution')
plt.show()
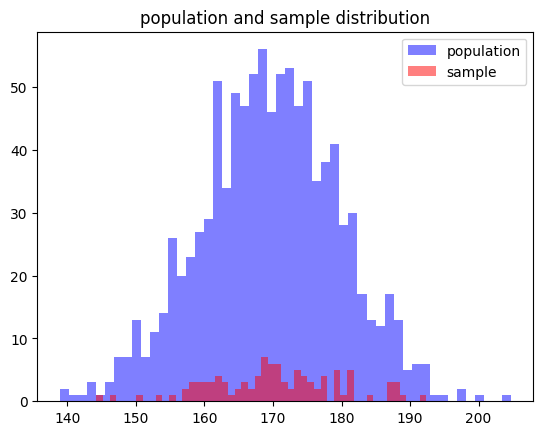
: 데이터 갯수에 대해서는 차이가 있지만, 모집단과 표본의 평균이 170 근처라는 점을 통해 표본이 모집단의 형태와 비슷하다는것을 알수 있음.
표본오차와 신뢰구간
표본오차
표본에서 계산된 통계랑과 모집단의 진짜 값 간의 차이
-표본의 크기 : 크기가 클수록 표본오차는 줄어든다.
-표본 추출방법 : 무작위 추출 방법을 사용하면 표본오차를 줄일수 있음.
신뢰구간
모집단의 특정 파라미터(평균,비율)에 대해 추정된 값이 포함될것으로 기대되는 범위를 나타냄.
- 신뢰구간 = 표본평균±z × 표준오차
여기서 z는 선택된 신뢰수준에 해당하는 z-값
예를 들어, 95% 신뢰수준의 z-값은 1.96. 일반적으로 95% 신뢰수준을 많이 사용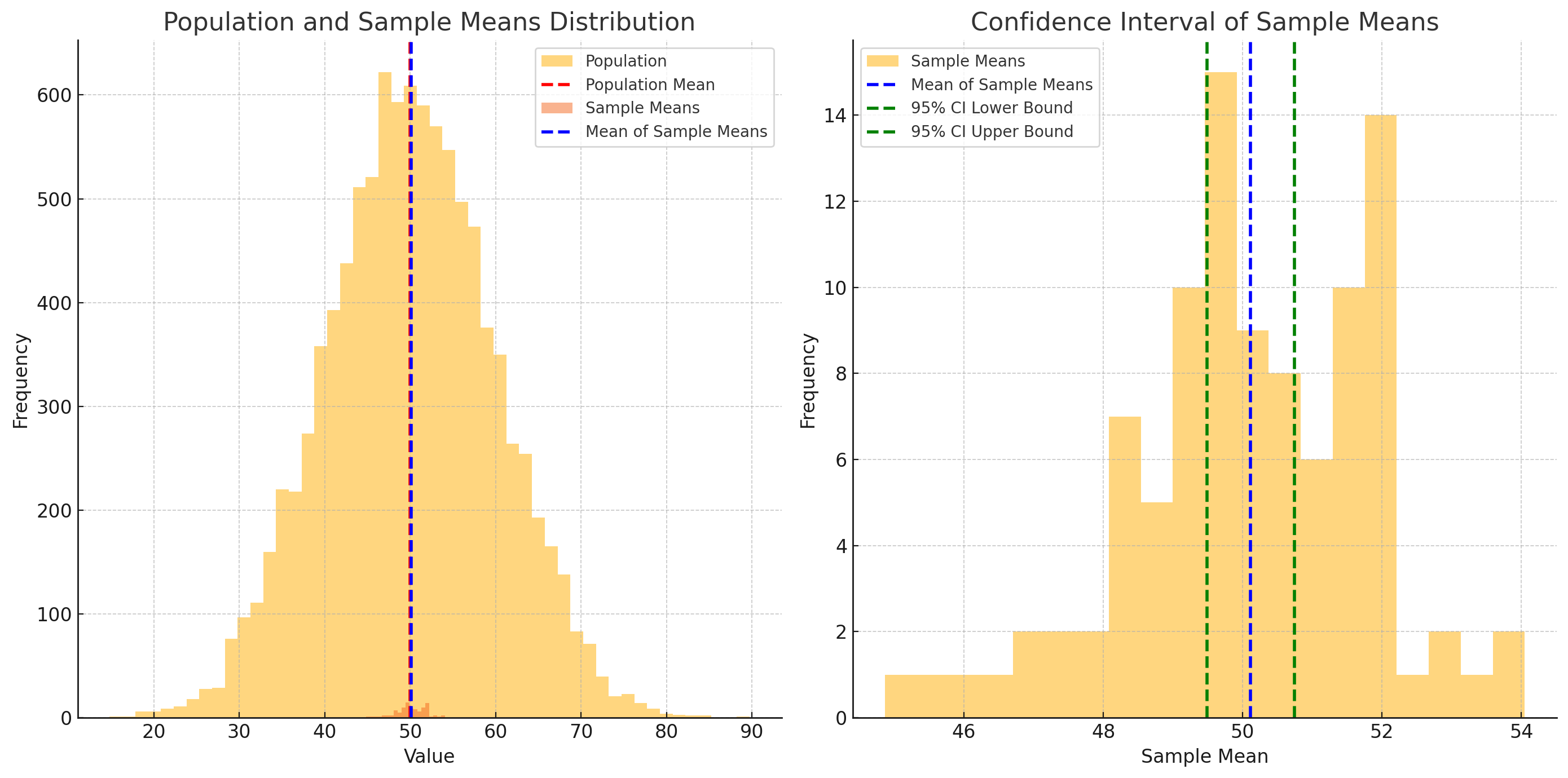
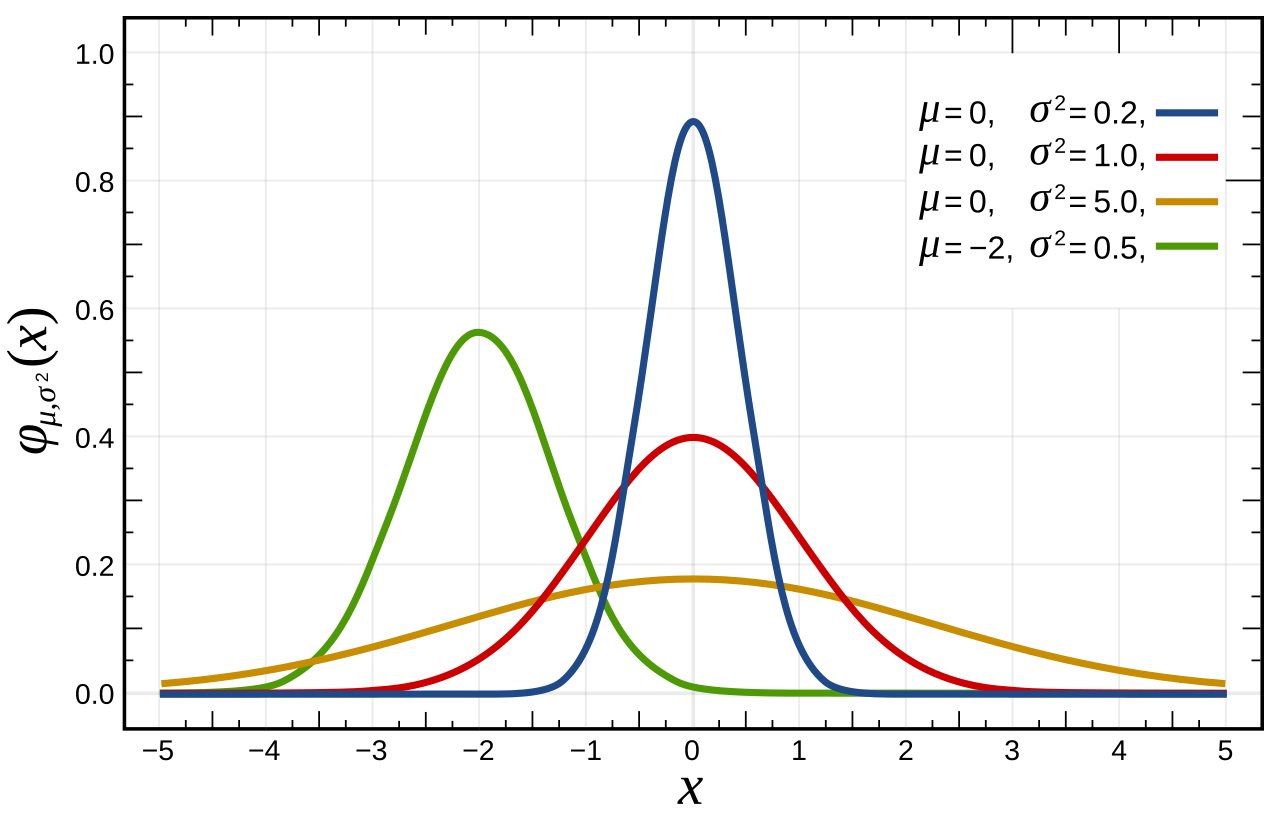
정규분포란?
종 모양의 대칭분포로 평균주위에 몰려있는 분포
평균에서 멀어질수록 데이터의 빈도 감소
파이썬 실습
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 정규분포 생성
normal_dist = np.random.normal(170, 10, 1000)
# 히스토그램으로 시각화
plt.hist(normal_dist, bins=30, density=True, alpha=0.6, color='g')
# 정규분포 곡선 추가
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, 170, 10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('normal distribution histogram')
plt.show()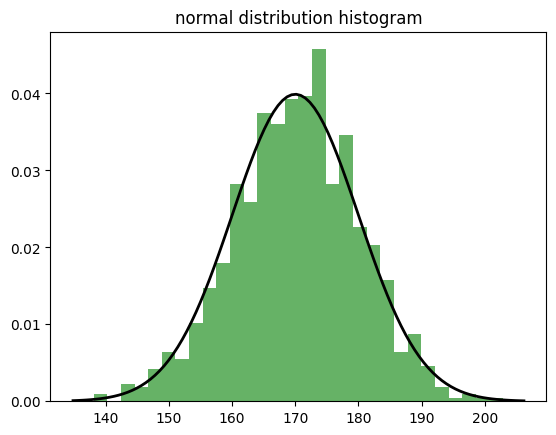
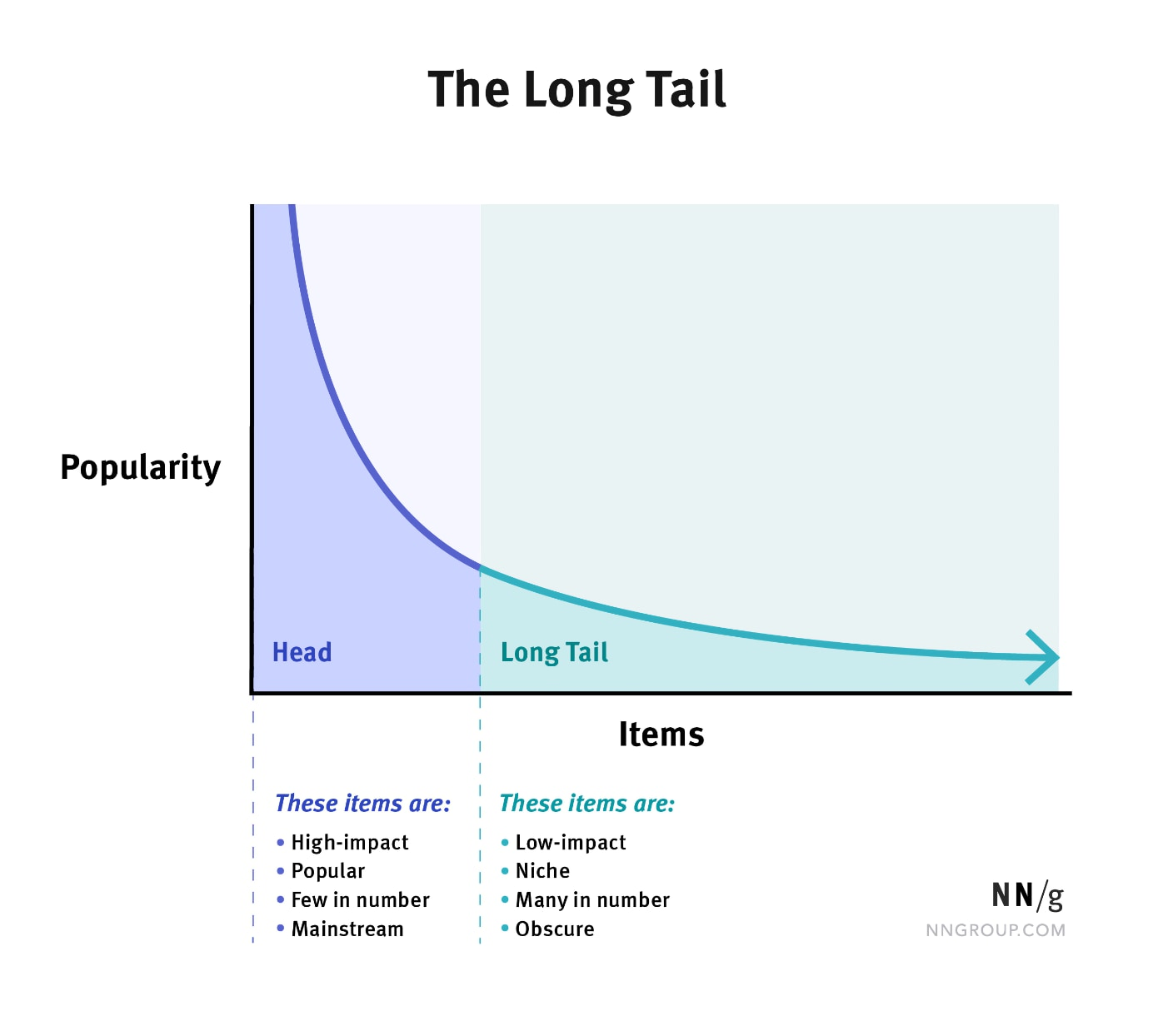
긴꼬리분포
데이터의 분포가 한쪽 끝에 몰려있고, 반대쪽으로 긴꼬리가 이어지는 형태의 분포
잘 팔리는 상위20%가 전체매출의 80% 차지
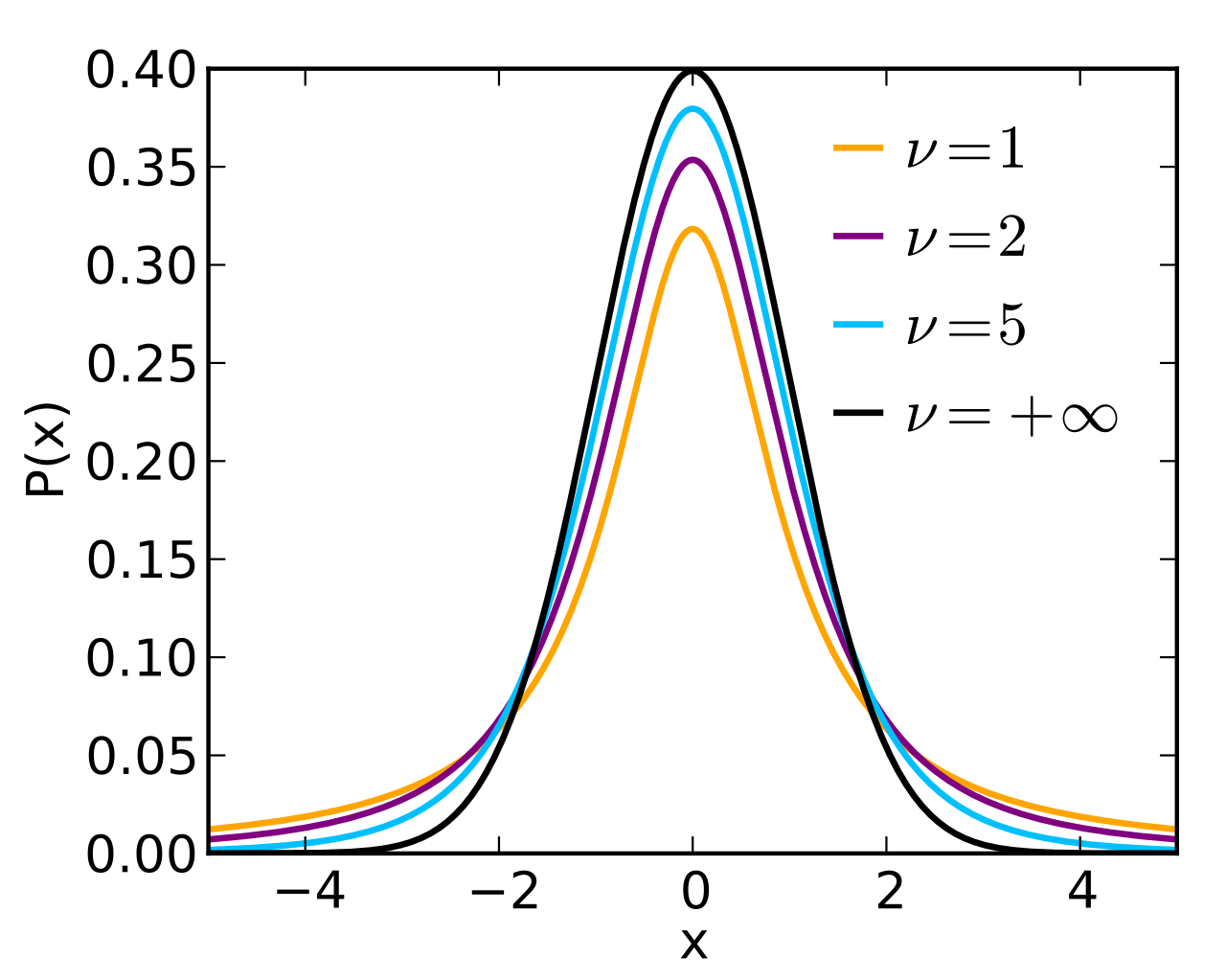
스튜던트 t분포
표본이 작을때 정규분포 대신 사용!
정규분포와 유사하지만, 표본의 크기가 작을수록 꼬리가 두꺼워짐.
파이썬 실습
# 스튜던트 t 분포 생성
t_dist = np.random.standard_t(df=10, size=1000)
# 히스토그램으로 시각화
plt.hist(t_dist, bins=30, density=True, alpha=0.6, color='r')
# 스튜던트 t 분포 곡선 추가
x = np.linspace(-4, 4, 100)
p = stats.t.pdf(x, df=10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('student t distribution histogram')
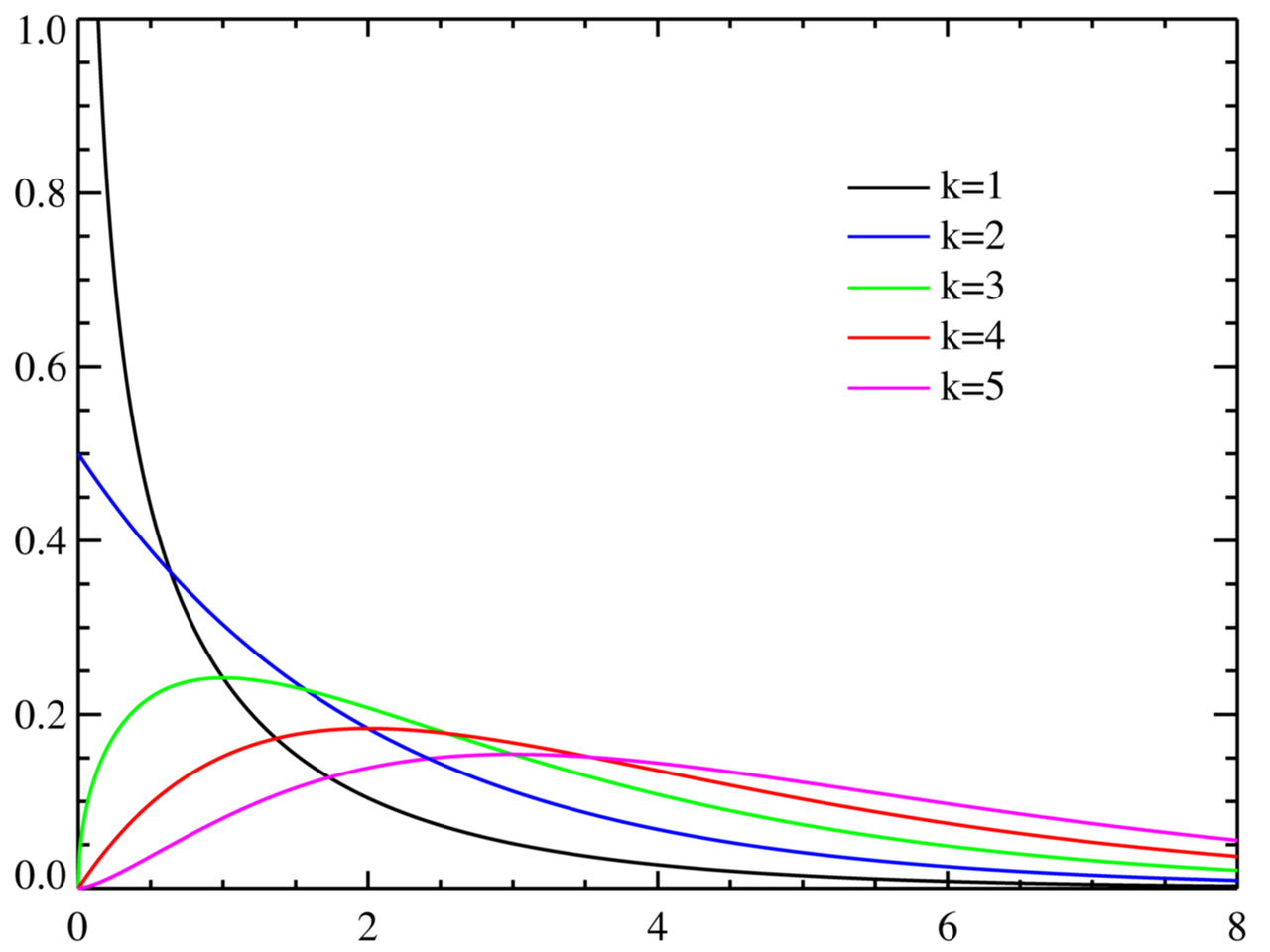
plt.show()카이제곱분포
범주형 데이터의 독립성 검정이나 적합도 검정에 사용되는 분포
ex) 성별이나 나이에 따른 선거후보 지지율
이항분포
결과가 2개 나오는 상황일때 사용
성공/실패 와 같은 두가지 결과를 가지는 실험을 여러번 반복했을때 성공횟수 분포
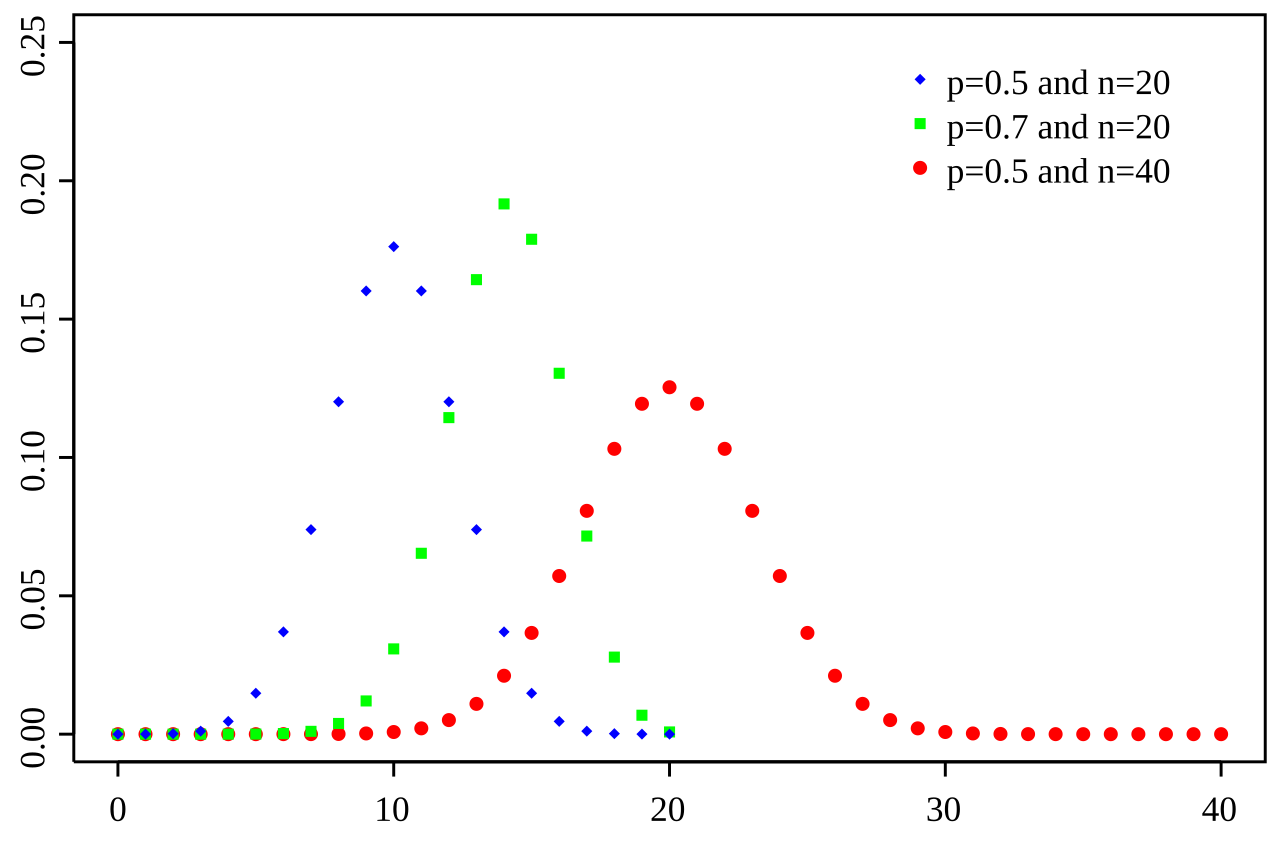
푸아송 분포
휘귀한 사건이 발생할때 사용하는 분포
이항분포처럼 연속된 값을 가지지 않음
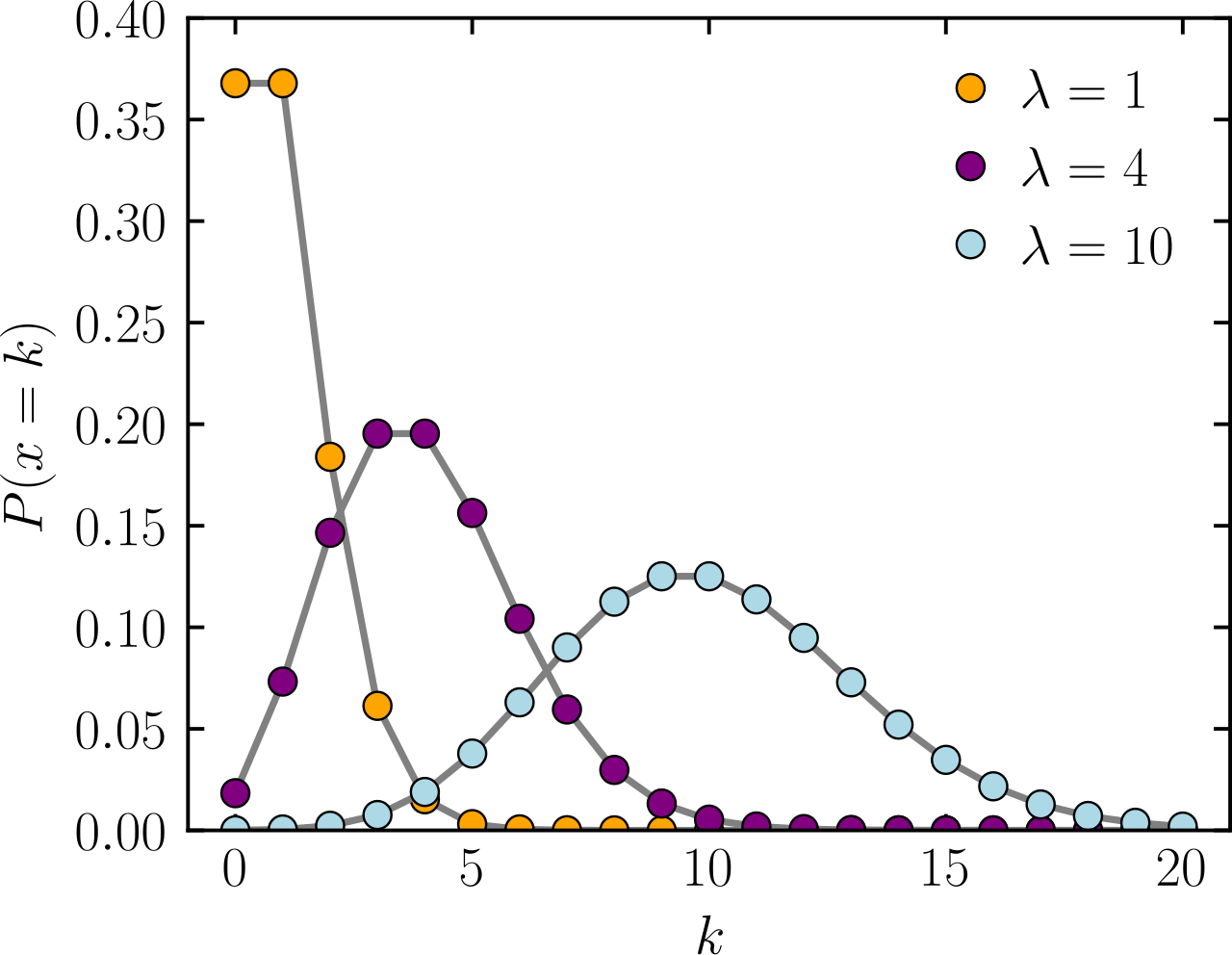
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# 푸아송 분포 파라미터 설정
lambda_value = 4 # 평균 발생률
x = np.arange(0, 15) # 사건 발생 횟수 범위
# 푸아송 분포 확률 질량 함수 계산
poisson_pmf = poisson.pmf(x, lambda_value)
# 그래프 그리기
plt.figure(figsize=(10, 6))
plt.bar(x, poisson_pmf, alpha=0.6, color='b', label=f'Poisson PMF (lambda={lambda_value})')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution')
plt.legend()
plt.grid(True)
plt.show()📊 분포 정리
1) 데이터수가 충분 -> 정규분포
2) 데이터수가 적다 -> 스튜던트 t분포
3) 일부 데이터가 전체적으로 큰 영향을 미침-> 롱테일분포(파레토분포)
4) 범주형 데이터의 독립성 검정이나 적합도 검정 -> 카이제곱 분포
5) 결과가 두개만 나오는 상황 -> 이항 분포
✅유의성 검정
-
A/B 검정
: 두 그룹을 비교, 우연히 일어난건지 통계적으로 유의미한지를 확인.
-
가설검정
: 데이터가 특정 가설을 지지하는지 검정하는게 포인트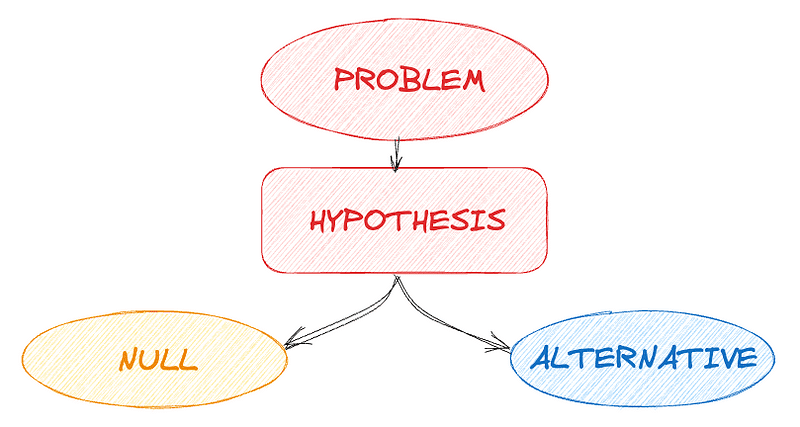
귀무가설(H0) 대립가설(H1) 을 설정하고, 귀무가설을 기각할지 결정.💡단계
- 귀무가설과 대립가설 설정
- 유의수준 결정
- 검정통계랑 계산
- P값과 유의수준 비교
(🔸P-값 일반적으로 P값이 0.05 미만이면 결과를 통계적으로 유의) - 결론도출