통계 라이브세션 4회차
상관관계와 선형회귀
- 상관과 회귀
상관관계 : 두 연속형 변수 사이에 함께 중가/감소 하는 패턴이 있는지를 수치로 표현한것.
-1<= 상관관계 <=1
상관관계는인과관계가 아니다.
- 상관관계 확인방법 -시각화
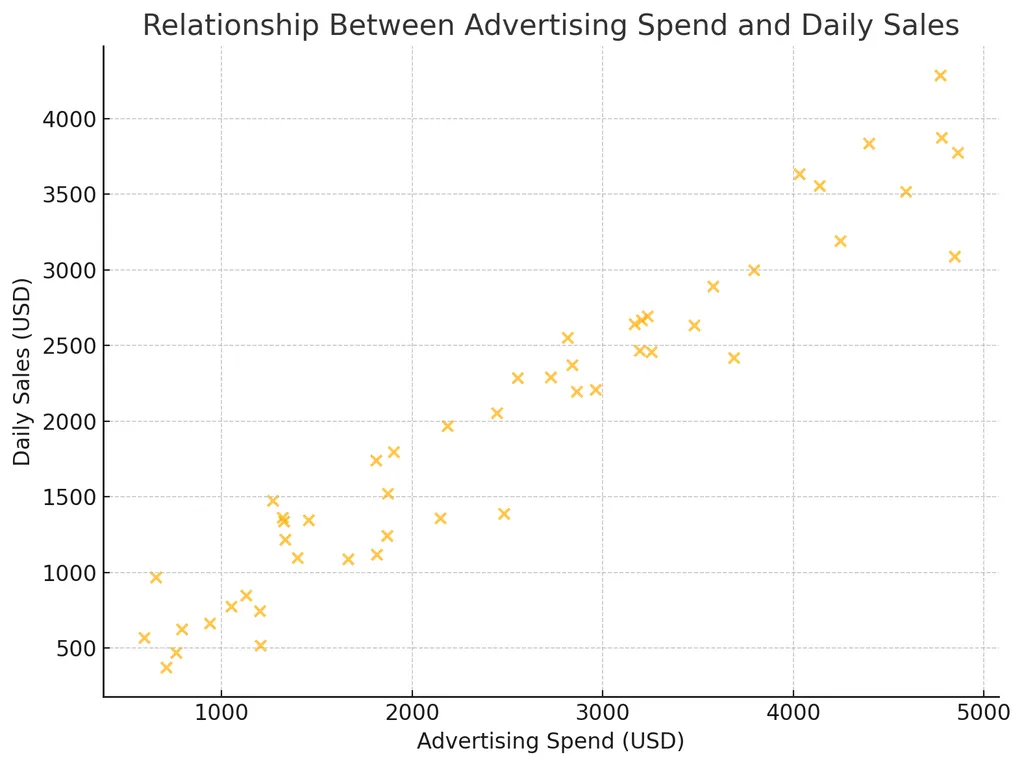
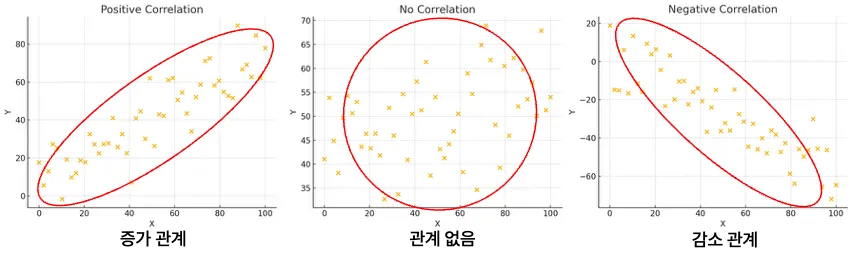
산점도: 두 연속형 변수의 관계를 시각적으로 확인하는 가장 기본적인 방법
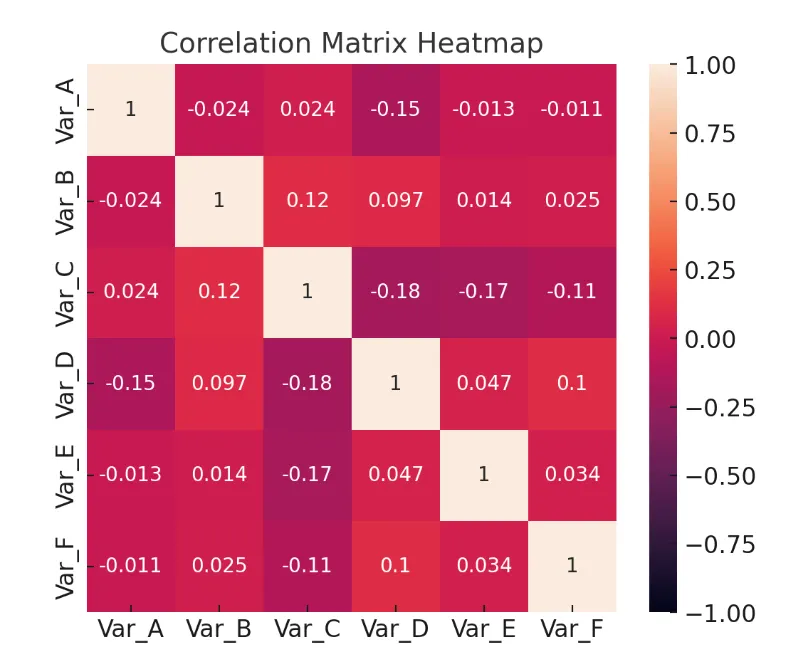
상관행렬 히트맵 : 변수들이 여러개일때, 각 변수 쌍마다 상관계수(피어슨, 스피어만 등) 를 계산하여 행과 열에 변수명을 배치한표.
상관계수
: 두 연속형 변수 사이의 관계를 숫자로 나타낸값.
-
피어슨 상관계수
공분산을 표준화한 값으로 두 변수의 선형관계를 -1~ 1 사이 숫자로 표현한것
공분산(두 변수가 함께 움직이는 정도)
=> 공분산을 두 변수의 표준편차로 나누어 단위 영향을 제거한 값이 상관계수(r) -
피어슨 상관계수를 사용할때 주의점
-상관의 세기는 도메인마다 달라짐
-이상치에 매우 민감(산점도와 함께 볼것)
-비선형 관계를 파악하지 못한다
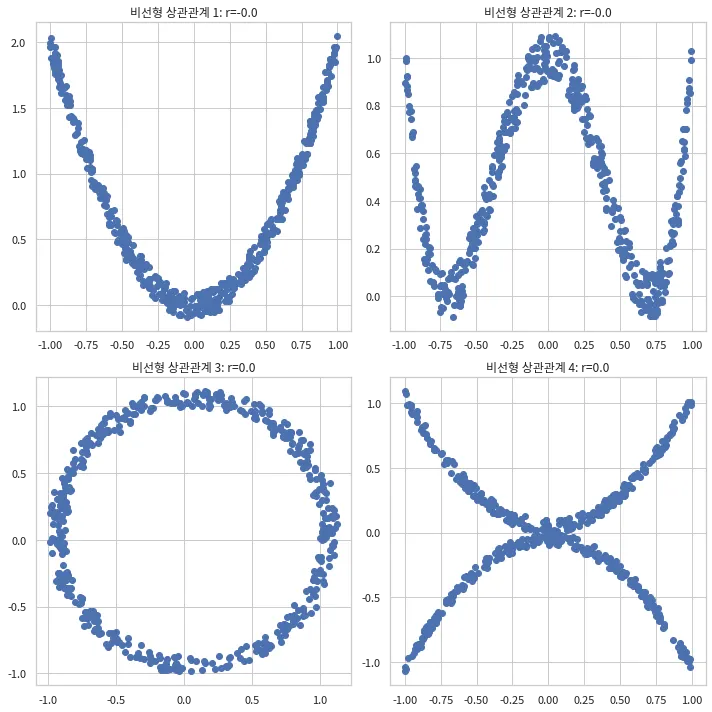
스피어만 순위상관계수
: 두 변수의 값보다 순서(순위)가 비슷하게 움직이는지를 보는 상관계수
-
왜 순위를 볼까?
-비선형 관계를 잘 잡을 수 있다.
-이상치 영향이 훨씬 적다.
-점수,등수,랭킹, 우선순위 등 무엇이 더 크고 작냐가 중요한 경우에 적합.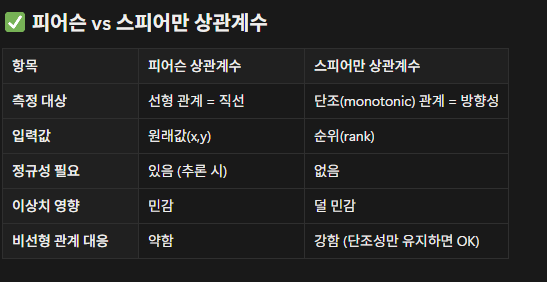
피어슨을 좀더 많이 사용함.
- 상관계수 사용이유?
-두 변수 간 관계의 방향성과 강도를 빠르게 이해하기 위한 가장 기본적인 도구
회귀
y = f(x) 형태의 함수를 통해 X가 변하면 Y가 어떻게 변하는지 수식으로 모델링하는 방법
- 기본적인 회귀모델
선형회귀:
-x가 변할때 y가 일정한 비율(직선관계)로 변한다고 가정하는 모델
단순선형회귀 :
하나의 독립 변수만 사용하는 경우 , 최대한 직선으로 x-y 관계를 설명하는것
- 회귀계수의 가설검정
우리가 구한 x,y 사이에 실제로 관계가 있다고 말할수 있을까?
- 귀무가설(H₀): (X와 Y 사이에 관계가 없다)
- 대립가설(H₁): (X와 Y 사이에 관계가 있다)
🔥회귀모형 평가
회귀분석은 모든 점에 대해 정확한 예측이 아니라 전체적으로 어떤 패턴이나 경향이 있는지를 설명해야한다.
-
잔차표준오차(RSE)
평균적으로 예측이 얼마나 빗나갔는지를 나타내는 값 -
결정계수()
오차만 줄이는게 아니라 데이터의 전체적인 변화를 얼마나 잘 설명하고 있는지를 숫자로 보여주는 지표
다중회귀
다중선형회귀란?
- 단순선형회귀는 독립변수가 1개일때만 사용가능
- 현실에서는 Y에 영향을 주는 원인이 여러개인 경우가 대부분
가설검정
1) 모형 전체가 의미 있는가? F검정
2) 각 변수는 의미 있는가? T검정
📊 통계 라이브세션 5회차
로지스틱 회귀
분류란?
입력값을 통해 미리 정의된 범주 중 하나로 분류하는 문제
-
오즈와 오즈비
성공이 실패보다 몇배 더 많은가를 나타낸것이 오즈, 두 그룹의 오즈를 비교한값이 오즈비확률은 얼마나 늘었는지만 보여주지만,
오즈는 몇배 유리해졌는지 보여줌. -
로짓 함수
오즈에 로그를 씌운 형태(로그 오즈)
오즈는 곱셈적 특징때문에 선형적 관계 이루지 않음.로지스틱 회귀란?
확률을 예측하고 오즈비를 통해 x가 증가하면 성공 가능성이 몇배로 변하는지 설명하는 모델
📌
① 로지스틱 회귀는 “확률을 예측하는 모델”이다. ⇒ 이진 분류 문제에 적용하는 모형
② 확률을 직접 선형식으로 예측할 수 없기 때문에 logit 변환을 사용한다.
③ 최종 출력은 시그모이드(sigmoid)를 통해 다시 확률로 변환된다.
④ 계수 β는 ‘오즈비(odds ratio)’로 해석한다.
모형평가지표
- 혼동행렬
: 예측값과 실제값을 비교해서 정답/오답 네가지로 분류한표 (TP, FP, TN, FN)
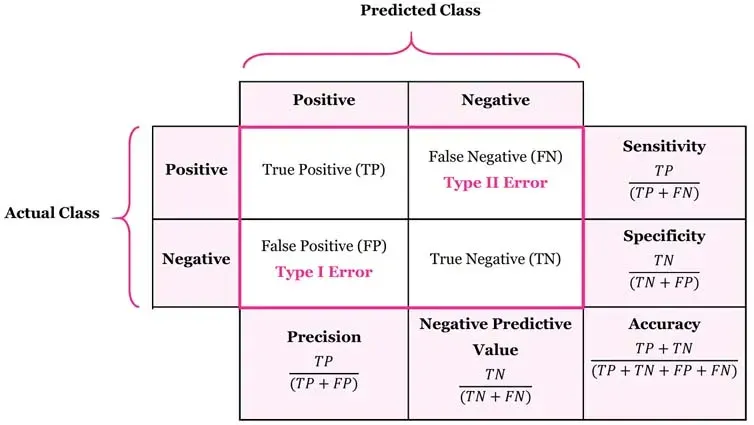
🔸 평가 지표
| 지표 | 설명 | 사용 상황 |
|---|---|---|
| 정확도(Accuracy) | 전체 중 맞춘 비율 | 클래스 비율이 균형 잡혀있을 때 |
| 정밀도(Precision) | 예측한 것 중 맞춘 비율 | False Positive가 민감할 때 |
| 재현율(Recall) | 실제 있는 것 중 맞춘 비율 | False Negative가 민감할 때 |
| F1-Score | 정밀도와 재현율의 조화 평균 | 둘 다 중요할 때 |
| ROC Curve, AUC | 다양한 임계값에서 모델 성능 시각화 | 모델 전반 평가용 |
