[CV] Edge Detection(2) - Cany Edge Detector

Yeontachi·2025년 8월 14일

Computer Vision Note

목록 보기

25/47

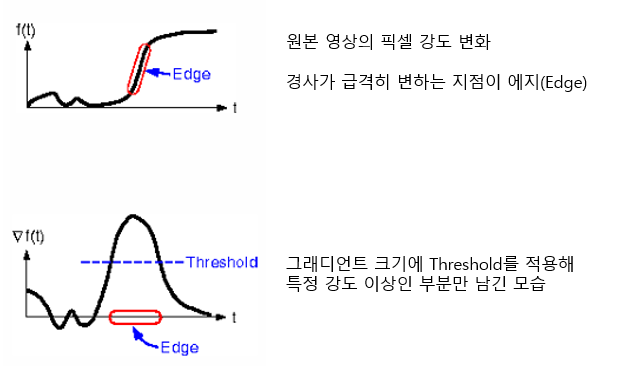
Canny Edge Detector는 1986년 J.Canny가 제안한 에지 검출 알고리즘으로, 현재까지도 가장 널리 사용되는 에지 검출 기법 중 하나이다. 기존의 Sobel, Prewitt, Laplacian 등의 단순 마스크 기반 에지 검출 방법에 비해 정확도와 안정성이 높으며, 잡음 억제와 에지 위치 정확도를 동시에 고려하는 점이 특징이다.

이 알고리즘의 설계 목표는 다음 세 가지로 요약된다.

1. 낮은 오류율(Low error rate)

가능한 모든 실제 에지를 검출하고, 에지가 아닌 부분은 검출하지 않는 것
잡음이나 불필요한 세부 사항에 의한 거짓 검출(False detection)을 최소화한다.

2. 정확한 위치(Localization)

검출된 에지 픽셀이 실제 에지 위치와 가능한 가깝도록 한다.
즉, 검출 결과의 공간적 오차를 최소화한다.

3. 단일 에지 응답(Single edge point response)

실제 하나의 에지가 존재하는 위치에서 여러 개의 픽셀이 연속적으로 에지로 검출되는 현상을 방지한다.
이중 응답(double response)을 억제하여 깨끗한 단일 픽셀 에지 맵을 생성한다.

Canny 알고리즘은 이러한 목표를 달성하기 위해 다음과 같은 절차를 따른다.

가우시안 필터를 이용한 노이즈 제거
1차 미분 연산을 통한 그래디언트 계산
비최대 억제(Non-maximum suppresstion)를 통한 에지 얇게 만들기
이중 임계값(Double thresholding)과 히스테라시스(Hysteresis)로 강한/약한 에지 연결

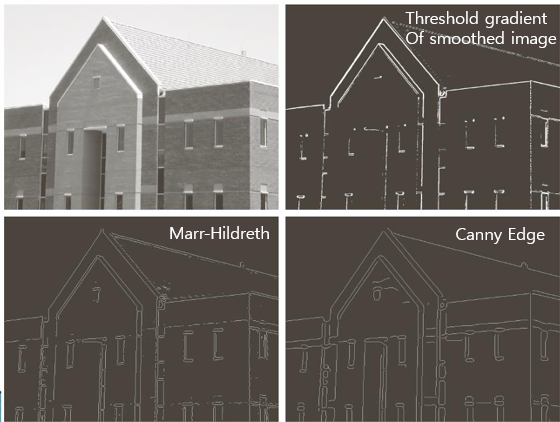
The Canny Edge Detector

위 그림은 원본 영상과 그래디언트 크기(norm of the gradient) 영상이다. 즉, 오른쪽은 각 픽셀의 밝기 변화 강도를 계산한 결과이다. 그래디언트 크기가 큰 영역일수록 경계가 뚜렷하게 나타나며, 이는 에지 후보가 될 가능성이 높다.

Canny 알고리즘에서는 먼저 가우시안 스무딩을 통해 잡음을 제거한 뒤, x방향과 y방향으로 영상의 미분을 수행하여 $g_x$ 와 $g_y$ 를 얻는다. 이를 이용해 그래디언트 크기를 다음과 같이 계산한다.

|∇f| = \sqrt{g_x^2 + g_y^2}

이 값이 바로 norm of the gradient이며, 영상 내 각 지점의 에지 강도를 나타낸다. 이 결과를 임계값(thresholding)으로 필터링하면, 강한 에지 영역만 남게 된다.

그러나 위 과정을 거친 후에도, 아래 그림처럼 에지는 여전히 굻은 띠 형태로 존재한다. 이는 그래디언트 크기가 에지 중심뿐 아니라 주변 픽셀에서도 비교적 높은 값을 갖기 때문이다.

그렇다면 이 두꺼운 에지 띠를 어떻게 하면 단일 픽셀 두깨의 매끄러운 곡선 형태로 변환할 수 있을까?

이를 해결하기 위해 비최대 억제(Non-maximum Suppression) 과정이 적용된다. 이 단계에서는 에지 방향을 따라 이웃 픽셀과 비교하여, 국소적으로 가장 강한 에지 픽셀만 남기고 나머지는 제거한다. 그 결과 두꺼운 띠 형태였던 에지가 얇고 선명한 곡선으로 바뀌어 최종 에지 맵의 기반이된다.

Non-Maximum Suppression

비최대 억제(Non-maximum Suppression, NMS)는 Canny Edge Detector에서 두꺼운 에지 영역을 단일 두께의 선으로 만드는 과정이다.

임계값 처리 이후의 그래디언트 크기 영상에는 에지 중심뿐만 아니라 주변 픽셀도 비교적 큰 값을 갖기 때문에, 그대로 사용하면 에지가 띠 형태로 두껍게 남는다. 이를 해결하기 위해 NMS는 그래디언트 방향을 따라 국소적으로 가장 강한 에지 픽셀만 남기고 나머지를 제거한다.

핵심 원리는 다음가 같다.

1. 각 픽셀의 그래디언트 방향을 계산한다.

2. 그래디언트 방향을 따라 양 옆 이웃 픽셀과 비교한다.

**3. 현재 픽셀이 국소 최대값이면 유지, 그렇지 않으면 제거(0으로 설정)한다.

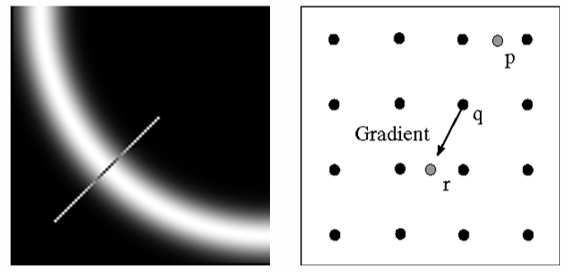
왼쪽 그림의 흰색 곡선 띠는 임계값 처리 후 남은 두꺼운 에지 영역이다. 대각선 선분은 해당 위치에서의 그래디언트 방향을 나타낸다. 이 방향을 기준으로 양 옆 픽셀과 비교하여 중심선만 남기는 작업을 수행한다.

오른쪽 그림에서 q는 검사 중인 픽셀이다. 화살표는 그래디언트 방향을 나타내며, p와 r은 q와 같은 방향선 위에 있는 이웃 픽셀들이다. q의 그래디언트 크기를 p와 r과 비교하여, q가 가장 크면 유지, 그렇지 않으면 제거하는 과정을 반복하여 두꺼운 에지들을 없애고, 중심선만 남게 된다.

Hysteresis thresholding

히스테리시스 임계값(Hystersis Thresholding)은 Canny Edge Detector의 마지막 단계로, 유효한 에지만 남기고 잡음을 제거하는 과정이다.

이 단계에서는 두 개의 임계값(High, Low)을 사용하여 에지를 세 가지로 분류한다.

강한 에지(Strong edge)
- 그래디언트 크기가 High 이상인 픽셀
- 확실한 에지로 분류되어 최종 에지 맵에 포함된다.
약한 에지(Weak edge)
- 그래디언트 크기가 Low 이상 High 미만인 픽셀
- 단독으로는 에지를 확정할 수 없지만, 강한 에지와 연결되어 있으면 유지된다.
Non-edge
- 그래디언트 크기가 Low 미만인 픽셀
- 최종적으로 제거된다.

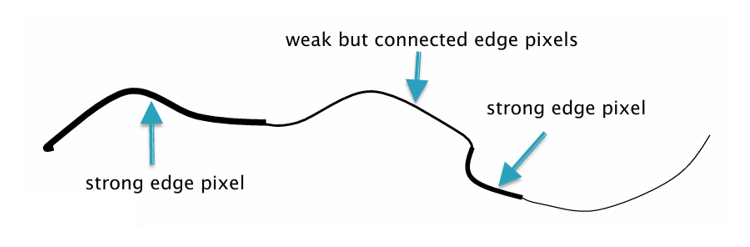
위 그림의 굵은 검은 선은 NMS를 거친 후 남아 있는 에지 후보이다. 화살표로 표시된 strong edge pixel들은 High 임계값 이상을 가지므로 확실한 에지로 즉시 선택된다.

Weak but connected edge pixels는 Low~High 범위의 값이지만, Strong edge와 연결되어 있기 때문에 에지로 유지된다. 반대로 연결되지 않은 약한 에지는 최종적으로 제거된다.

히스테리시스 임계값의 장점은 연속성을 유지하면서 노이즈로 인한 단절이나 잘못된 에지 검출을 최소화한다는 것이다.

즉, 강한 에지 주변의 약한 에지를 살려 경계선이 끊기지 않게 하고, 잡음처럼 고립된 약한 에지는 제거한다.

Final Canny Edges

추가 설명 High? Low?
여기서 “High 이상”이라는 표현은
그래디언트 크기( $M(x,y) = \sqrt{G_x^2 + G_y^2}$ )가 설정한 높은 임계값(High threshold)보다 크거나 같은 경우를 의미한다.

수치적으로 설명

Canny Edge Detector에서는 그래디언트 크기 $M(x,y)$ 가 0~255 범위(8비트 영상)로 표현되는 경우가 많다.
이때 High와 Low 임계값은 보통 절대값이나 비율로 지정한다.
- 절대값 방식 예시:
  - Low = 50, High = 100
  - $M(x,y) \geq 100$ → 강한 에지(Strong edge)
  - $50 \leq M(x,y) < 100$ → 약한 에지(Weak edge)
  - $M(x,y) < 50$ → 비에지(Non-edge)
- 비율 방식 예시(OpenCV 기본 동작):
  - High = 0.2 × (최대 그래디언트 값)
  - Low = 0.1 × (최대 그래디언트 값)
  - 예를 들어 최대값이 200이면, High=40, Low=20이 된다.

Effect of $\sigma$ in Canny Edge Detector

Canny 에지 검출에서 $\sigma$ 는 가우시안(Gaussian) 필터의 표준 편차를 의미하며, 이는 에지 검출 전 단계에서 노이즈를 제거하기 위해 적용하는 가우시안 스무딩의 정도로 결정한다.

$\sigma$ 가 작을 때 (Small $\sigma$ )
- 가우시안 커널의 폭이 좁아, 스무딩 효과가 약하다.
- 세부적인 구조나 미세한 패턴까지 보존되어 에지로 검출된다.
- 하지만 잡음(Noise)도 그대로 남아, 불필요한 에지가 많이 생길 수 있다.
$\sigma$ 가 클 때(Large $\sigma$ )
- 가우시안 커널이 넓어져 강한 스무딩 효과가 발생한다.
- 세부적인 구조가 사라지고, 크고 뚜렷한 경계선 위주로 에지가 검출된다.
- 잡음이 크게 줄어들지만, 작은 디테일은 손실될 수 있다.