[CV] Intensity Transformation(3) - Histogram Processing

Yeontachi·2025년 8월 1일

AI Computer_Vision

Computer Vision Note

목록 보기

10/47

히스토그램 처리(Histogram Processing)은 영상의 밝기 값 분포를 분석하고 조정하는 기법으로, 디지털 영상 처리에서 가장 기본적이고 중요한 역할을 한다.

히스토그램은 영상에서 각 픽셀의 밝기 값(그레이 레벨)이 얼마나 자주 나타나는지를 보여주는 그래프이다. X축은 밝기 값(0~255), Y축은 해당 밝기 값의 픽셀 개수를 의미한다.

이 정보를 기반으로 다음과 같은 처리가 가능하다.

대비(Contrast) 향상 : 어두운 영상 또는 너무 밝은 영상의 대비를 조정
밝기 조정 : 영상이 전반적으로 너무 어둡거나 밝을 때 조정
세부 특징 강조 : 의학 영상, 위성 사진, 저조도 영상에서 세부 정보 강화

그 중 가장 널리 사용되는 기법은 히스토그램 균일화(Histogram Equalization)이며, 이는 픽셀 값이 가능한 범위 (0~L-1)에 균일하게 분포되도록 조정하여 대비를 향상시킨다.

Histogram for image processing

히스토그램 정의는 아래와 같다.

h(r_k) = n_k

$r_k$ : k번째 그레이 레벨(0~L-1)
$n_k$ : 레벨 $r_k$ 를 가진 픽셀 수

//Example 8bit Image
unsigned int Histogram[256] = {0}; 

for(h = 0; h < H; h++) //영상의 세로
	for(w = 0; w < W; w++){ //영상의 가로
    	Histogram[img[w][h]]++; //img[w][h]는 좌표 (w, h)에 있는 픽셀의 밝기 값 r_k
    }
//결과: Histogram[k]에는 밝기 값이 k인 픽셀의 총 개수가 저장됨(위 식과 동일)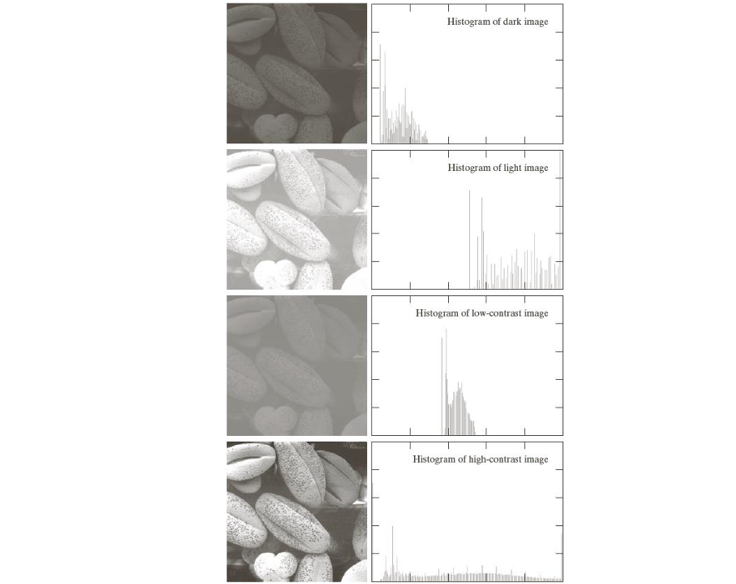

Histogram의 X축은 픽셀의 밝기 값(그레이 레벨)로, 왼쪽(0)에서 오른쪽(255)로 갈수록 밝아진다. Y축은 각 밝기 값에 해당하는 픽셀의 개수(빈도, Frequency)를 의미하며, 값이 클수록 해당 밝기 값을 가진 픽셀이 많다는 의미이다.

정규화 히스토그램(Normalized Histogram)

p(r_k) = \frac{n_k}{MN}

$M \times N$ : 영상 크기
$p(r_k)$ : 밝기 값 $r_k$ 의 확률

누적 분포 함수(CDF)

C(r_k) = \sum_{j=0}^k p(r_j)

Histogram Equalization

히스토그램 평활화는 픽셀 밝기 값의 분포를 재조정하여 영상의 대비(contrast)를 향상시키는 기법이다.

원본 영상의 히스토그램이 특정 영역(예: 어두운 쪽)에 집중되어 있을 때, 이 값들을 전체 밝기 범위(0~255)에 고르게 분포시키는 것이 목적이다. 그 결과, 영상은 더 선명해지고, 세부 정보가 잘 드러나며, 어두운 이미지 $\to$ 고대비 이미지로 변화한다.

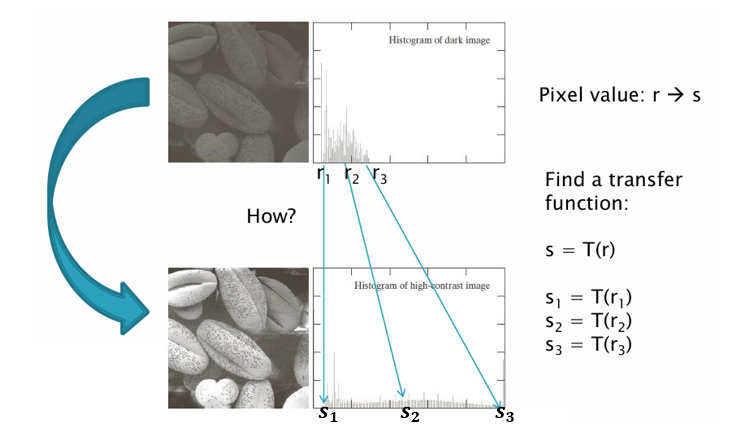
전체적으로 어두운 위쪽 이미지의 Histogram의 경우 대부분의 픽셀 값이 왼쪽(어두운 영역)에 몰려있다.(저대비)

대비가 향상된 아래쪽 이미지의 Histogram은 픽셀 값이 0~255 전체에 걸쳐 고르게 분포(고대비)되어 있는 모습을 확인할 수 있다.

원래 픽셀 값 $r_1, r_2, r_3$ 에 대해 새로운 값을 매핑하는 Transfer Function을 정의하여,

s = T(r)

새로운 값 $s_1, s_2, s_3$ 로 매핑 시키는 작업이 히스토그램 평활화(Histogram Equalization)이라고 부른다.

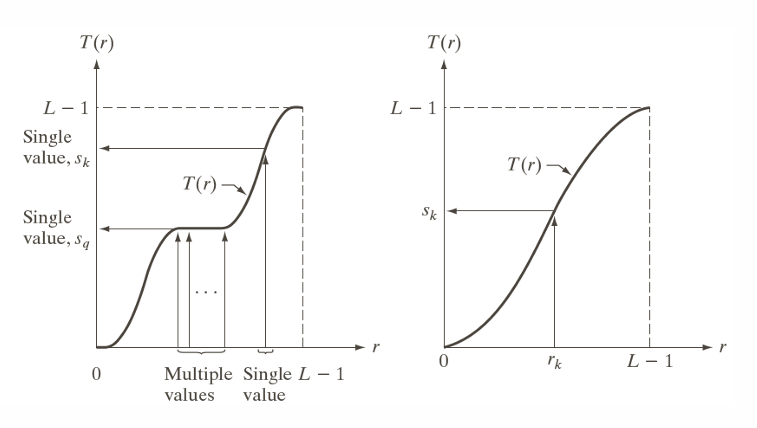
좌측 Histogram을 보면, 특정 구간에서는 여러 입력 값이 같은 출력 값으로 매핑됨을 확인할 수 있다. 이런 평평한 구간에서는 정보 손실 가능성이 있다.

우측 Histogram은 단조 증가 함수 형태로 가장 이상적인 형태이다. 모든 입력 값이 고유한 출력 값으로 매핑되며 이 경우 정보 손실이 발생하지 않는다.

히스토그램 평활화 전후의 히스토그램 상태를 살펴보면,

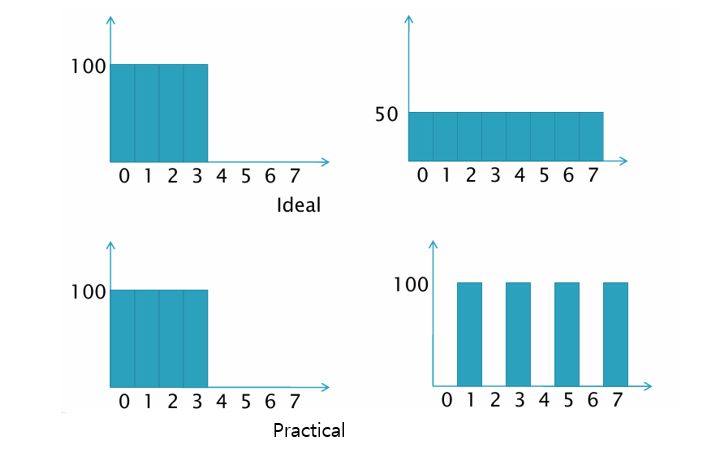
원본 영상(저대비 영상)의 히스토그램은 현재 값이 특정 구간(0-3)에 몰려 있다. Histogram Equalization으로 값이 균등하게 펴진 우측 Histogram 형태를 원하지만, 이것은 이론상 이상적인 결과이며, 실제로는 하단 Histogram 예제와 같이 완벽히 균등 분포가 되지는 않는다.

히스토그램 평활화는 픽셀 값 분포를 균등하게 재배치하려 하지만, 실제로는 근사적으로 수행됨을 알 수 있다.

이러한 히스토그램 평활화(Histogram Equalization) 변환 함수는 CDF(누적 분포 함수)에 기반한다.

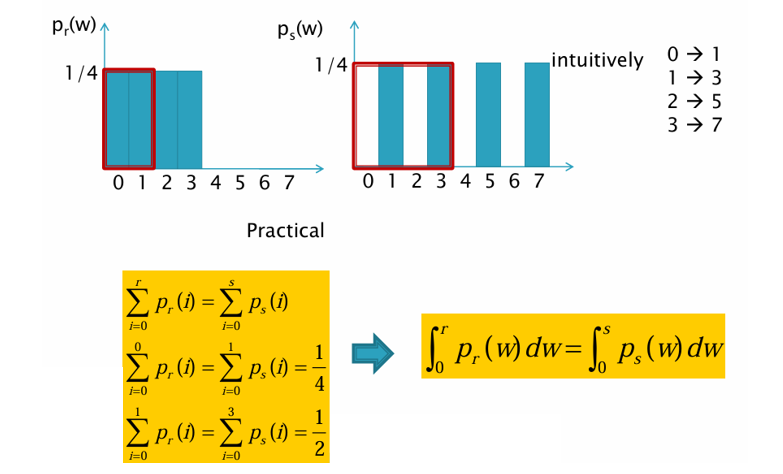
$p_r(w)$ : 원본 영상 픽셀 값의 확률 분포
$p_s(w)$ : 평활화 후 목표 확률 분포(균등 분포)

위 이미지의 빨간색 박스 부분을 누적 확률(CDF)을 이용해 매핑을 하면,

원본 값 0 $\to$ 변환 후 값 1
원본 값 1 $\to$ 변환 후 값 3
원본 값 2 $\to$ 변환 후 값 5
원본 값 3 $\to$ 변환 후 값 7

즉, 변환된 값 $s$ 는 원본 값 $r$ 의 누적 확률과 동일한 누적 확률을 갖도록 매핑하는 것이 히스토그램 평활화(Histogram Equalization)이다.

식으로 정리하면 아래와 같다.

\sum_{i=0}^{r} p_r(i) = \sum_{i=0}^{s} p_s(i)\\\\

\int_{0}^{r} p_r(w) \, dw = \int_{0}^{s} p_s(w) \, dw

이때 $p_s(w) = \frac{1}{L-1}$ 이므로,

\int_{0}^s p_s(w)\,dw = \frac{s}{L-1}\\ c =\frac{s}{L-1}

즉, 변환 함수 $T(r)$ 은

s = (L-1)\int_{0}^{r} p_r(w) \, dw = T(r)

변환 함수 $T(r)$ 은 새로운 값 $s$ 는 원본 값 $r$ 의 $CDF \times (L-1)$ 로 결정되며 즉, 원본 히스토그램의 누적확률을 이용해 픽셀 값을 재매핑한다는 의미이다.

이것이 히스토그램 평활화(Histogram Equalization)의 핵심 공식이며, 실제 구현은 누적 히스토그램을 정규화해서 픽셀 값에 적용한다.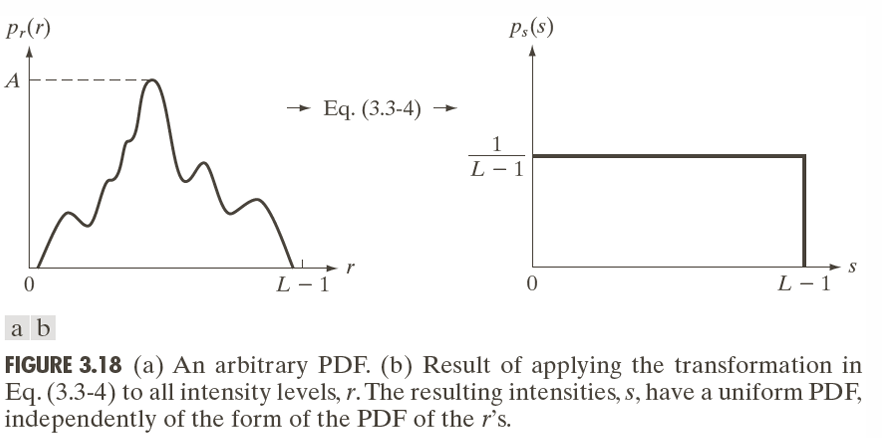
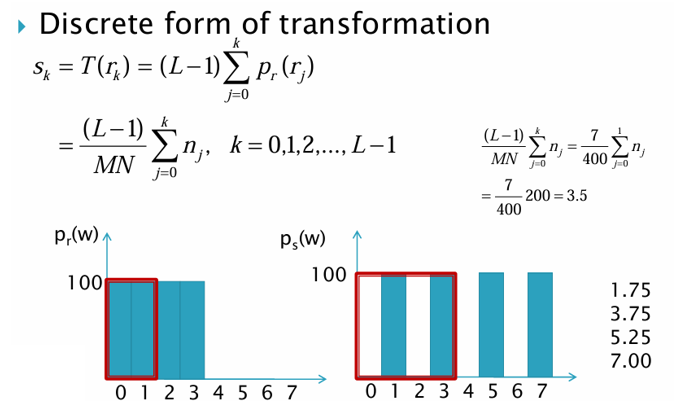
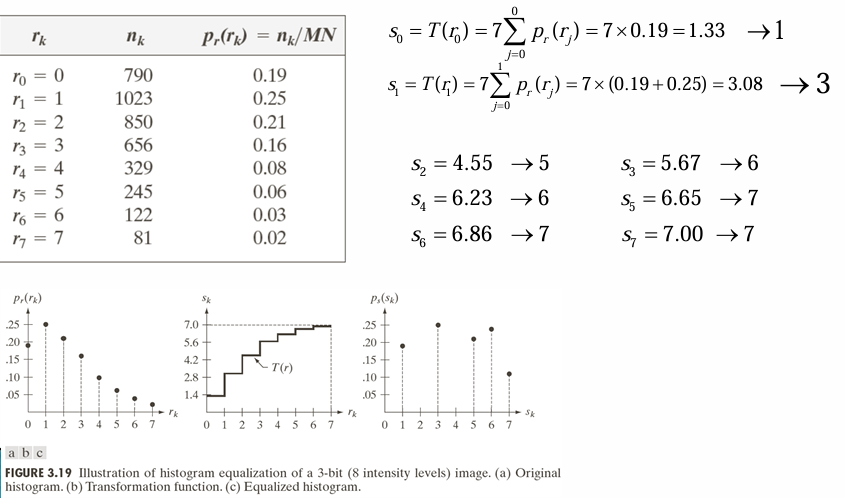
Example

Histogram Specification(Matching)

히스토그램 매칭(Histogram Matching, Histogram Specification)은 원본 영상의 픽셀 값 분포를 사용자가 원하는 목표 히스토그램 형태로 변환하는 과정이다.

히스토그램 평활화(Histogram Equalization)는 이 기법의 특수한 경우로, 목표 히스토그램이 균등(Uniform)한 경우이다.

히스토그램 매칭의 핵심 목표는 픽셀 값 분포를 재구성해 원하는 톤, 조명 특성, 대비를 구현하는 것이다.

주요 활용은 멀티센서 영상 정규화, 영화나 사진 후처리에서 특정 색감 구현, 의료 영상에서 특정 구조 강조 등에 활용된다.

Implementation

원본 영상의 밝기 값 확률 분포를 $p_r(r)$ , 목표 히스토그램의 확률 분포를 $p_z(z)$ 라고 한다. 이 두 분포를 직접 매핑하기는 어렵기 때문에, 각 분포를 누적분포함수(CDF)로 변환해 사용한다.

원본 영상의 각 밝기 값의 확률은 다음과 같이 계산된다.(확률 밀도 함수)

p_r(r_j) = \frac{n_j}{n}

$n_j$ : 밝기 값 r_j를 가진 픽셀의 개수
$n$ : 전체 픽셀 수

히스토그램 매칭은 픽셀 값 r에 대한 누적 확률을 동일하게 맞추는 원리로 동작한다. 따라서 위 확률 밀도 함수를 누적 분포 함수(CDF)로 변환한다.

원본 영상의 CDF

S(r_k) = \sum_{j=0}^k p_r(r_j)

목표 히스토그램의 CDF

G(z_k) = \sum_{j=0}^k p_z(z_j)

핵심 아이디어는 다음과 같다.

S(r_j) = G(z_i)

즉, 원본 영상에서 누적 확률이 $s(r_j)$ 인 픽셀 값은, 목표 히스토그램에서 동일한 누적 확률을 갖는 $z_i$ 로 변환한다.

이것을 수식으로 정리하면

z = G^{-1}(S(r))

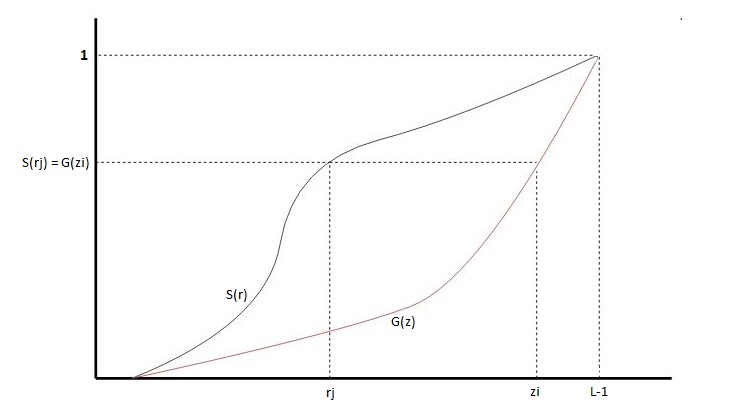
위 그래프를 기준으로 매핑을 하게 되면 원본 값 $r_j$ 의 누적 확률을 계산 $\to$ 동일한 확률을 갖는 목표 값 $z_i$ 로 변환

예를 들면, $S(r_j)$ = 0.6일 때, 목표 히스토그램의 CDF에서 0.6에 해당하는 z값을 찾아 매핑한다.

히스토그램 매칭은 픽셀 값의 순서를 유지하면서, 원하는 밝기 분포로 영상을 조정한다. 원본 영상과 목표 히스토그램이 다르더라도, CDF를 이용하면 두 분포 간의 매핑이 안정적으로 가능하다.

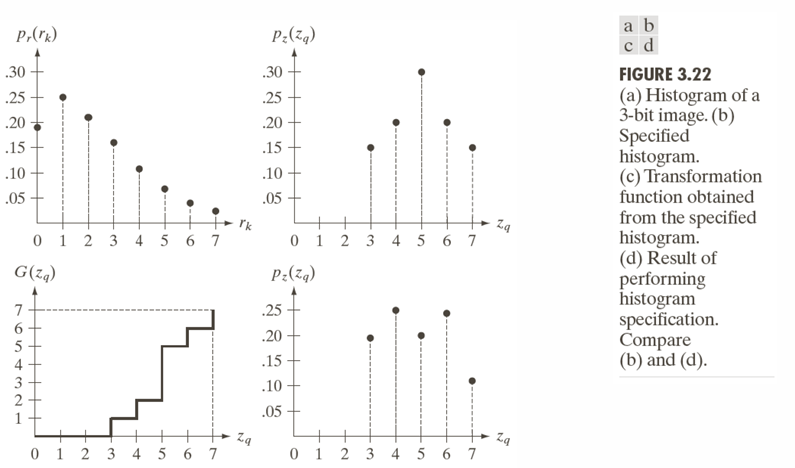
위 이미지의 (a)는 원본 영상의 히스토그램이다. 원본 영상은 어두운 톤(작은 값)이 많은 어두운 이미지이다.

(b) 이미지는 목표 히스토그램이다. 즉, 목표는 중간 톤 강조이다.

(d) 이미지는 히스토그램 명세(Histogram Specification) 이후 결과 이미지이다. 목표 히스토그램 (b)와 실제 결과 (d)를 비교해보면

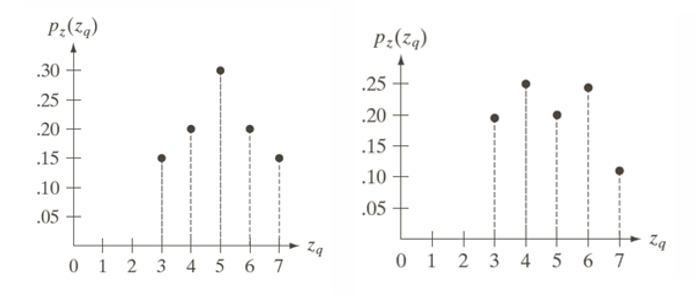
완벽히 동일하지는 않지만, 목표 형태와 유사함을 확인할 수 있다. 이것은 입력 값이 이산적이고 같은 값의 픽셀이 하나의 값으로만 변환되기 때문이다.

Example

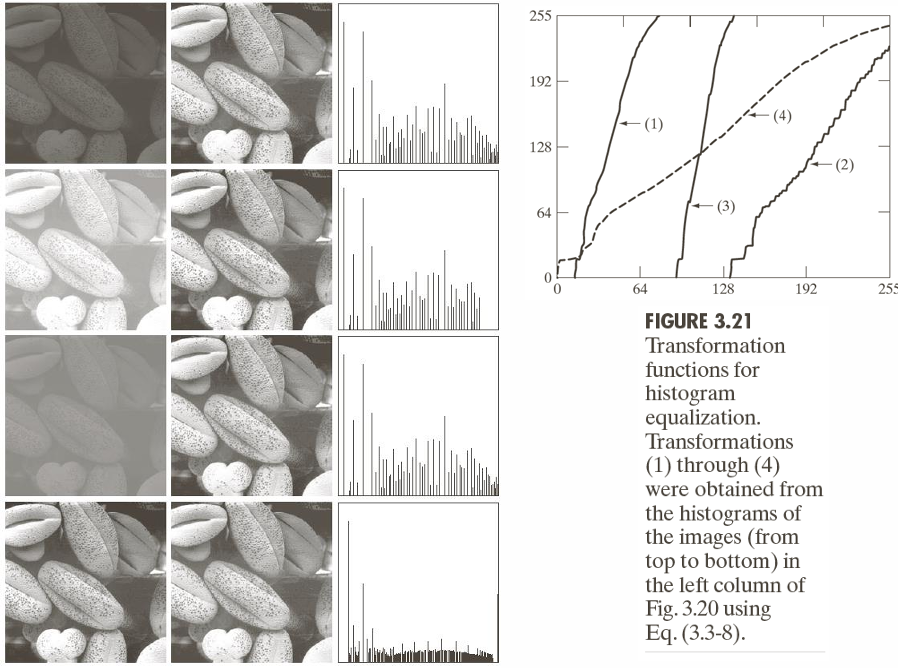
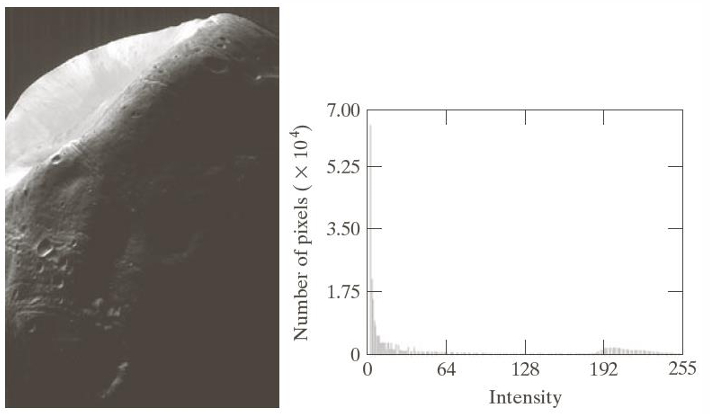
달 표면 이미지의 원본 이미지와 히스토그램이다. 대부분의 픽셀이 0~30 범위(어두운 영역)에 몰려 있어 영상이 매우 어둡고 디테일이 잘 보이지 않는다.

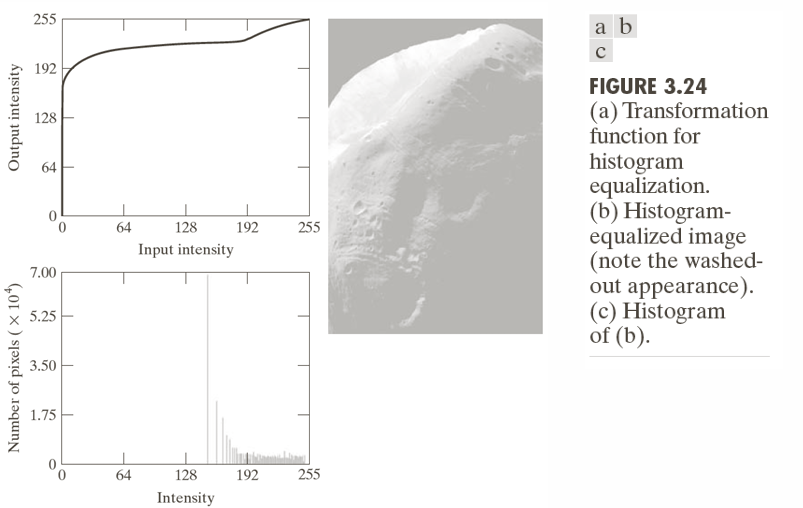
아래는 Histogram Equalization 결과 이미지이다. 좌상단 그래프는 변환 함수이고, 우측 영상은 Histogram Equalization 적용 결과 영상이다. 결과 히스토그램을 살펴보면 값이 한쪽으로 치우쳐져 있는 형태이며, 완벽한 균등 분포는 아님을 확인할 수 있다. 실제 영상도 너무 밝아지고 세부 톤이 사라진 느낌을 준다.

아래 영상은 Histogram Specification 결과이다. 명세화는 사용자가 지정한 히스토그램 형태를 목표로 하므로, 영상의 특성을 보전하면서 원하는 톤으로 조정이 가능하다.

Local Histogram Processing

히스토그램 평활화(Histogram Equalization)는 일반적으로 영상 전체(Global)의 히스토그램을 이용해 픽셀 값을 변환한다.
그러나 영상 전체에 대해 같은 변환 함수를 적용하면, 국소적인 대비(Local Contrast)가 잘 보존되지 않는 문제가 생길 수 있다.

이를 해결하기 위해 사용하는 기법이 지역 히스토그램 처리(Local Histogram Processing)이다.

전체 영상이 아닌, 작은 영역(이웃, Neighborhood)마다 별도로 히스토그램을 계산하고 그에 맞는 변환을 적용한다. 그 결과 로컬 대비가 강화된다. 즉, 국소적 세부 구조가 더 잘 드러나게된다.

작동 방식
(1) 이웃(Neighborhood) 정의

보통 $m \times n$ 크기의 윈도우(예: 3x3, 5x5 등)를 선택한다.

(2) 윈도우 이동

중심 픽셀을 기준으로 해당 영역의 히스토그램을 계산한다.

(3) 변환 함수 계산

그 영역에서 히스토그램 평활화 또는 히스토그램 명세화를 적용한다.

(4) 픽셀 값 변환

중심 픽셀의 값을 변환된 값으로 매핑한다.

(5) 다음 픽셀로 이동

윈도우를 한 픽셀씩 이동하면서 위 과정을 반복한다.

위 이미지에서 Original Image(a)는 네모 박스와 안쪽의 패턴이 있지만, 전반적으로 대비가 낮아 패턴이 잘 보이지 않는다.

Global Histogram Equalization 적용 결과(b), 영상 전체 대비는 향상되었으나, 일부 패턴은 여전히 잘 보이지 않는다.

Local Histogram Equalization 적용 결과(c),(윈도우 크기 3x3) 각 픽셀 주변 3x3 영역에서 히스토그램 평활화를 수행, 그 결과 로컬 대비가 크게 향상되어 숨겨져 있던 패턴(글자, 선, 원)이 뚜렷하게 보인다.

References

Images from Rafael C. Gonzalez and Richard E.
Wood, Digital Image Processing, 2nd Edition.

Histogram matching - Wikipedia https://en.wikipedia.org/wiki/Histogram_matching

Yeontachi

기초를 다지는 중입니다.📚🧑‍💻

이전 포스트

[CV] Intensity Transformation(2) - Piecewise-Linear Functions and Bit-Plane Slicing

다음 포스트