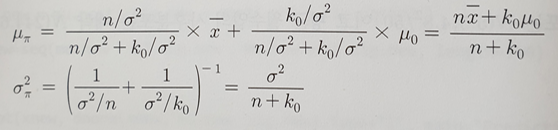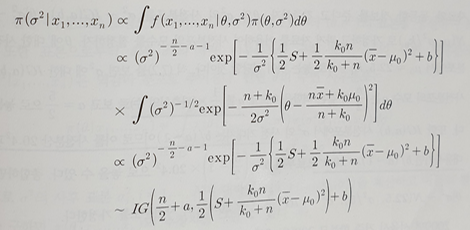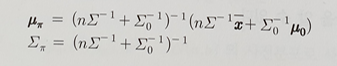7.1 평균의 추정과 예측분포
사후분포
- 자료: X1,...,Xn|θ ~ N(θ, σ^2)
- X.bar|θ ~ N(θ, σ^2/n)
- f(x1,...,xn|θ)가 x.bar를 통해서만 θ에 의존하므로 x.bar가 θ에 대한 충분통계량
- θ의 공액 사전분포: N(μ(0), σ(0)^2)
- 사후분포
π(θ|x1,...,xn) ∝ f(x.bar|θ)π(θ) ~ N(μ(π), σ(π)^2)
θ|x.bar ~ N(μ, σ^2)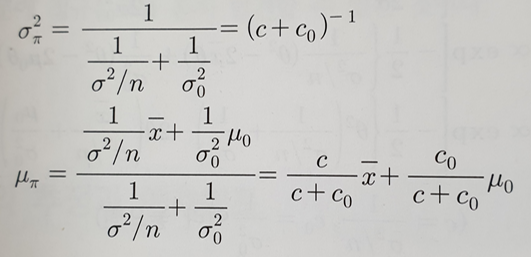
- 표본평균 x.bar의 정확도: c, 사전평균 μ(0)의 정확도: c0
- n이 크면 표본평균의 가중치가 커져서 μ(π)가 x.bar와 거의 일치하게 되고,
n이 작으면 μ(π)가 μ(0)의 영향을 상대적으로 많이 받음 - n이 크거나, 사전분산σ(0)^2이 표본분산σ^2에 비해 상당히 크면 σ(π)^2 = σ(0)^2 -> 사전분산이 매우 커서 사전분포의 영향이 거의 없기 때문
- c0>0이면 사전 정보가 있다는 것 의미, 사후추정치의 정확도는 표본추정치의 정확도보다 커짐
예측분포
- X(n+1)|θ ~ N(θ,σ^2)
θ|x1,...,xn ~ N(μ(π), σ(π)^2) - (X(n+1)-θ)|θ ~ N(θ-θ,σ^2) = N(0, σ^2) : θ와 무관 -> X(n+1)-θ와 θ는 독립
- (X(n+1)-θ)+θ|x1,...,xn ~ N(0+μ(π), σ^2+σ(π)^2) = N(μ(π), σ^2+σ(π)^2)
- X(n+1)의 예측평균 = θ의 사후평균
X(n+1)의 예측분산
= θ의 사후분산 σ(π)^2 + θ가 주어졌을 때 X(n+1)의 분산 σ^2 >= 표본분산, θ의 사후분산
ex. 7.2
무정보 사전분포
: π(θ) = 1
- 부적합(improper): 전체 실수 공간에서 적분값이 1이 아니므로 확률밀도함수가 아닌 사전분포 도는 사전밀도함수
- 이로부터 유도되는 사후분포 또는 사후밀도함수는 적분값이 1이 되어 적합한(proper) 밀도함수
- 사전분포가 부적합하더라도 사후분포만 적합하면 상관 없음(최종적으로 사용하는 것이 사후분포이기 때문)
θ의 사후밀도함수
θ|x1,...,xn ~ N(x.bar, σ^2/n)
- 95% 최대사후구간: x.bar ± 1.96 σ/sqrt(n)
= 빈도론적 최우 추정치 - 베이지안 해석: θ가 구간에 속할 확률이 95%
빈도론적 해석: n개의 표본을 반복적으로 추출하여 신뢰구간을 구하면, 그 중 95%의 구간은 θ를 포함. 주어진 구간은 이 중 하나이므로 θ가 이 구간에 속할 확률이 1일 확률이 95%
θ의 예측분포
X(n+1)|x1,...,xn ~ N(x.bar, σ^2/n+σ^2)
7.2 평균과 분산의 추정
평균 θ와 분산 σ^2이 둘 다 모수인 경우
- 결합사후분포
π(θ, σ^2|x1,...,xn) = f(x1,...,xn|θ, σ^2)π(θ,σ^2)/f(x1,...,xn) - 사전분포 π(θ, σ^2) = π(θ|σ^2)π(σ^2)
- π(θ|σ^2) ~ N(μ(0), σ^2/k0)
- μ(0): σ^2가 주어진 조건하에서 θ의 사전평균
- k0: 사전정보를 얻는 데 사용된 표본의 대략적인 개수(표본평균의 분산이 σ^2/n인 것과 같은 맥락)
- π(σ^2) ~ IG(a,b) 역감마분포
σ^2 ~ IG(a,b), θ|σ^2 ~ N(μ(0), σ^2/k0)인 경우
- X1,...,Xn|θ, σ^2 ~ N(θ, σ^2)
σ^2 ~ IG(a,b)
θ|σ^2 ~ N(μ(0), σ^2/k0) - θ|σ^2,x ~ N(μ(π), σ(π)^2)
- σ^2의 주변 사후밀도함수
σ^2|x1,...,xn ~ IG - 결합사후분포
π(θ, σ^2|x1,...,xn) = π(θ|σ^2,x1,...,xn) π(σ^2|x1,...,xn) - θ의 주변 사후밀도함수
: 결합사후분포를 σ^2에 대해 적분 - π(θ|x1,...,xn) 추정치
= π(θ|x1,...,xn,σ^2)/N (N: σ^2의 사후표본 개수)
π(σ^2) = 1/σ^2, π(θ) = 1, π(θ,σ^2) = π(θ)π(σ^2)인 경우
- θ|σ^2,x ~ N(x.bar, σ^2/n)
σ^2|x1,...,xn ~ IG((n-1)/2, S/2) - θ|x1,...,xn ~ t(n-1)(x.bar, s^2/n)
- 최대사후구간: x.bar ± t(n-1, α/2) x s/sqrt(n)
- 분산을 모를 경우 θ에 대한 고전적 추론의 결과와 일치
7.3 다변량 분포
공분산이 알려진 경우 평균의 추정
π(θ) ~ Np(μ(0), Σ(0))
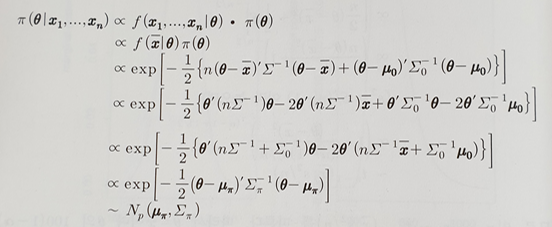
평균과 공분산의 추정
W ~ IW(v0, Λ0)
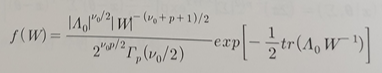

- 단변량인 경우와 마찬가지로 무정보 사전분포를 사용한 경우 고전적 θ 추정과 일치