선형대수 : 01. 벡터(Vector) - 1 : 벡터의 정의와 표기, 벡터의 기본적인 성질

❇️ 요약

• 벡터의 정의와 표기
• 벡터의 기본적인 성질

📖 벡터의 정의

🔆 벡터란? - 1

• 벡터라는 단어는 라틴어에서 비롯
• 옥스퍼드 사전에서 1704년에 출간된 존 해리스의 저서에 벡터라는 단어가 처음 등장
• 라틴어 Vector는 물건을 운반하는 물체를 뜻하며 영어로 Carrier로 번역 가능
• 우리 주변의 세계를 보고 이를 코드로 영리하게 묘사하는 방법
• 사과가 나무에서 떨어지고, 추가 공중에서 흔들리고, 지구가 태양을 중심으로 움직이는 현상 표현(크기와 방향성 필요)
• 모두 벡터(Vector) 개념이 들어가 있음
• 벡터는 사물의 움직임을 프로그래밍하기 위한 가장 기본적인 구성요소
• 벡터는 크기와 방향을 모두 가지는 어떤 양으로 정의

🔆 벡터란? - 2

• 벡터는 물리학 및 공학에서 벡터는 위치, 속도, 힘 등과 같이 크기와 방향성을 나타냄
• 공학에서는 벡터 공간이 유클리드 공간인 경우를 대부분 다룸
• 따라서, 유클리드 벡터(Euclidean Vector), 기하벡터(Geommetric Vector), 공간 벡터(Spatial Vector)라고 부름
• 벡터와 대비하여 크기만(길이, 높이, 질량, 에너지)을 갖는 대상을 스칼라(Scalar)라고 함
  

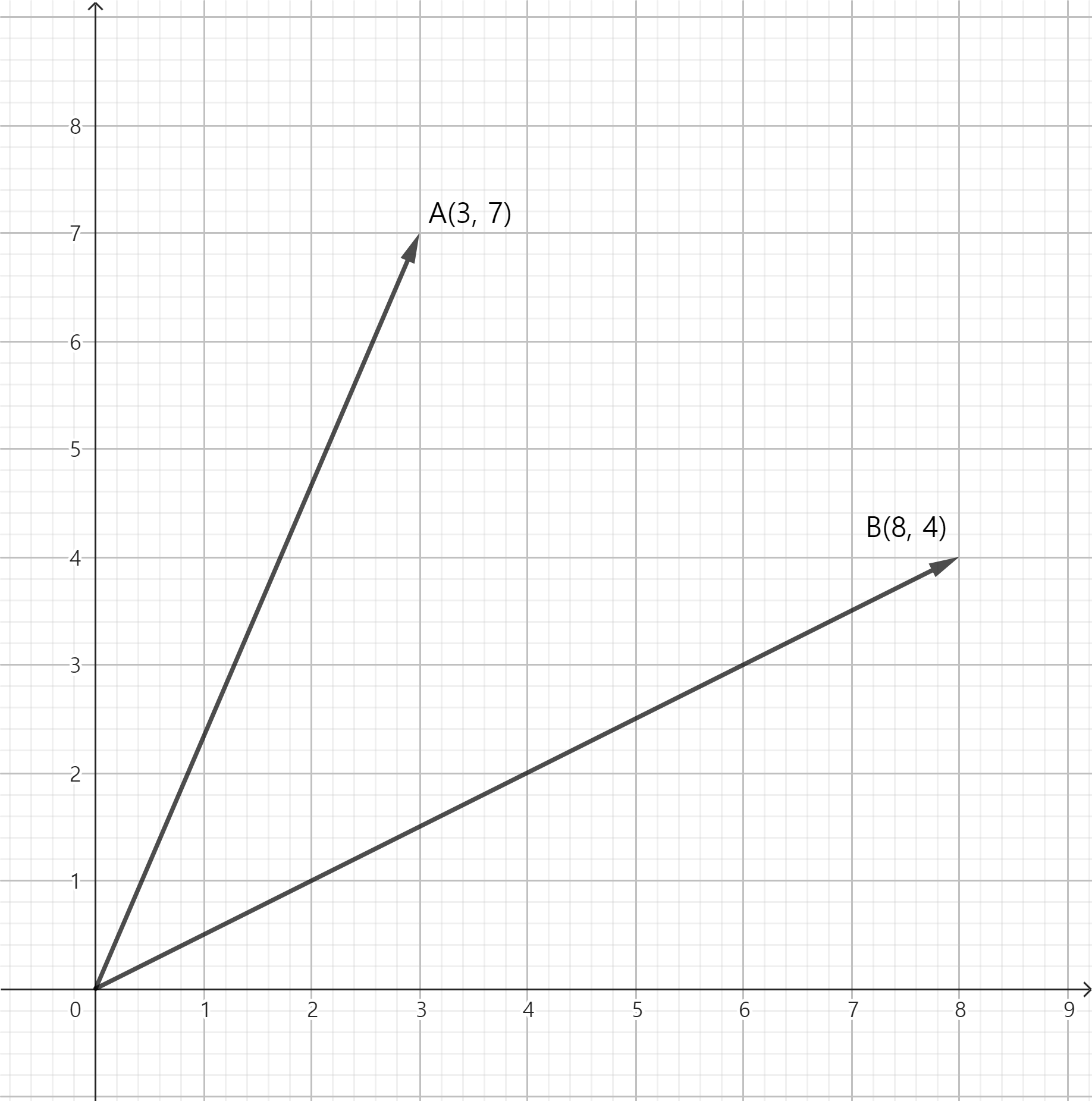
X의 힘이 8일때 Y의 힘이 4이면 B지점의 힘의 방향은 위 사진의 B지점과 같다.

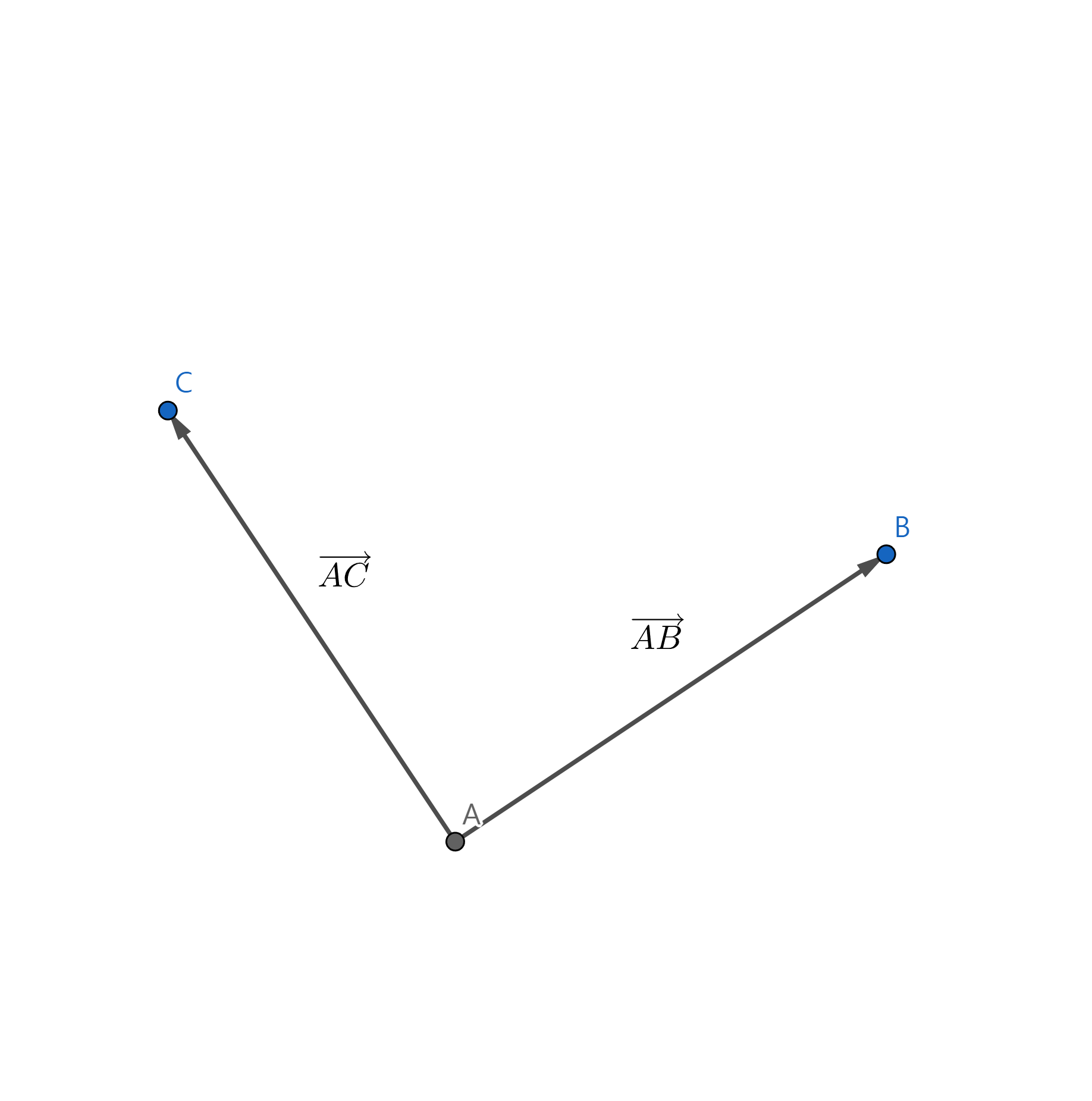
두 선의 크기는 같으나, 방향성이 다르다.

📖 벡터의 표기법

🔆 벡터의 표기법

• 한 벡터를 부호 $\large a$를 사용하여 나타낼 때, $\large a, \color{red}\vec{a}, \tilde{a}$ 등과 같이 표기함
• $\large a$의 크기만을 나타낼 때는 $\large \textcolor{red}{|a|}, a$ 등의 방법으로 표기
• 점 A에서 점 B를 향하며, 크기가 두 점 사이를 잇는 선분의 길이인 벡터를 부호로 사용하여 나타낼 때, 대게 $\color{red}\overrightarrow{AB}$와 같이 표현함
• A를 화살표 원점,기점,꼬리라고 하며 B는 화살표의 끝,종점,머리라고 표현

📖 벡터의 기본적인 성질

🔆 벡터의 기본적인 성질

• 동등성

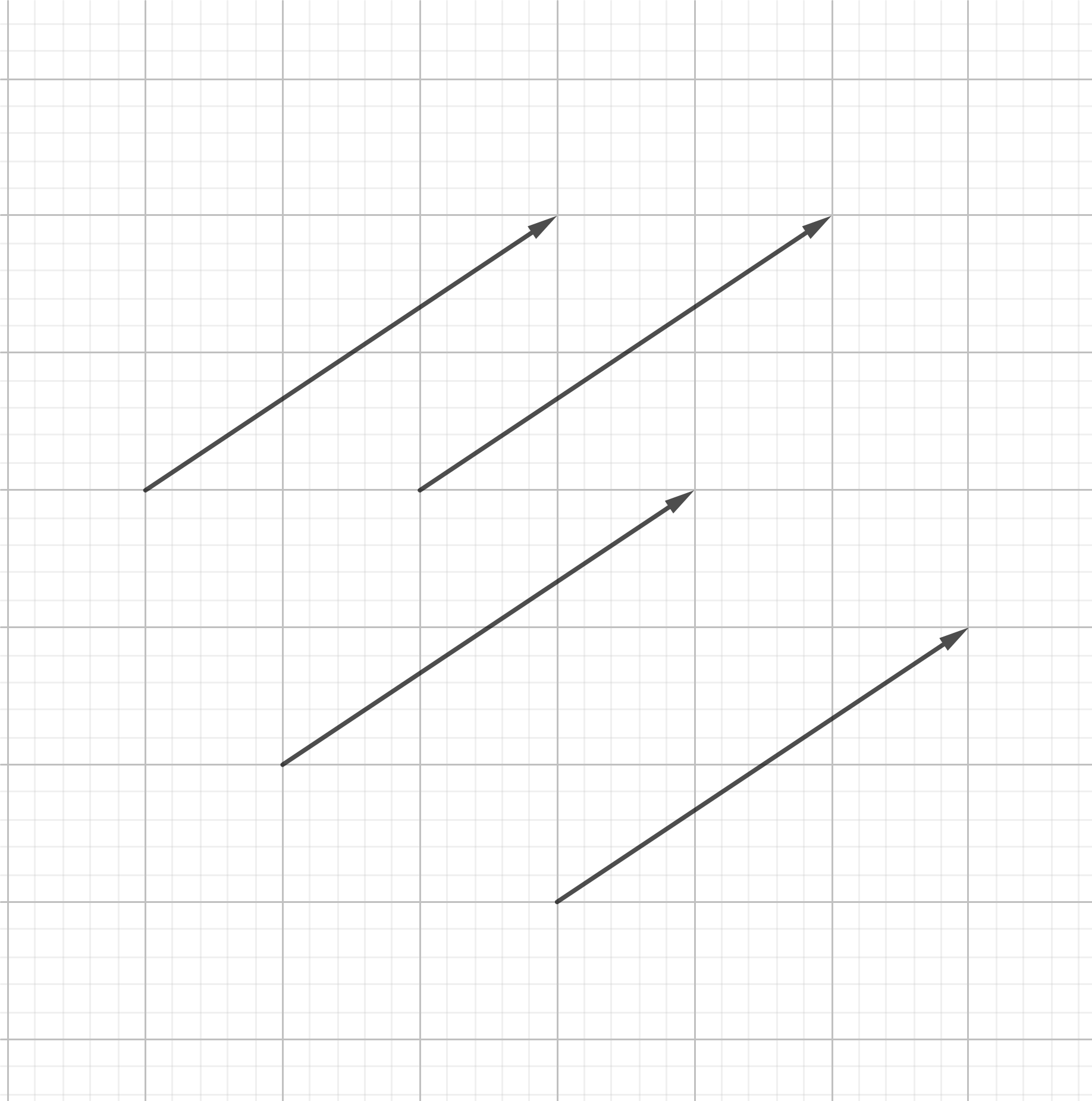
  • 벡터가 크기와 방향만을 가지므로 원점의 특정한 위치는 아무런 의미를 갖지 않음.
  • 즉, 원점이 일치하지 않더라도 두 화살표의 방향이 일치하고 그 크기가 같으면, 동일한 벡터임
    

• 영 벡터

  • 영벡터는 크기가 영인 벡터를 의미함
  • 방향성만 갖는 벡터

• 음 벡터

  • 벡터 $\text{a}$ 자신에 더했을 때 결과가 영벡터가 되는 벡터를 a의 음벡터라고 정의함
  • $\large \color{red}-\text{a}$로 표시하고 음벡터 $-\text{a}$는 $\text{a}$와 크기는 같으나 방향이 정반대인 벡터를 의미함

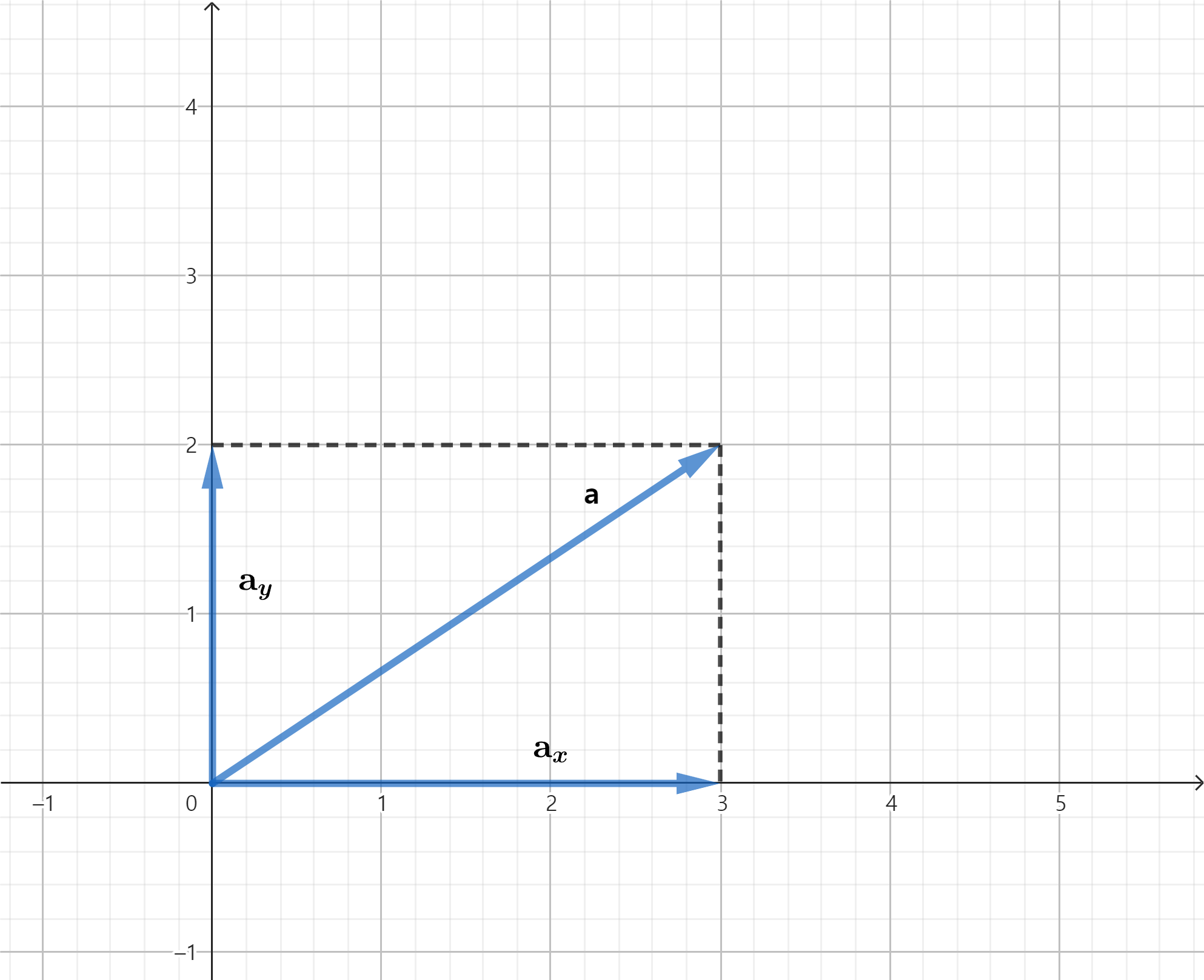
🔆 벡터의 좌표와 성분

• 벡터를 표현하는 방법으로 공간에 좌표계를 설정하여 좌표 값을 사용할 수 있음
• 기하학적으로 벡터를 다루는 방법보다 편리하며, 보다 체계적으로 정확한 계산을 할 수 있음
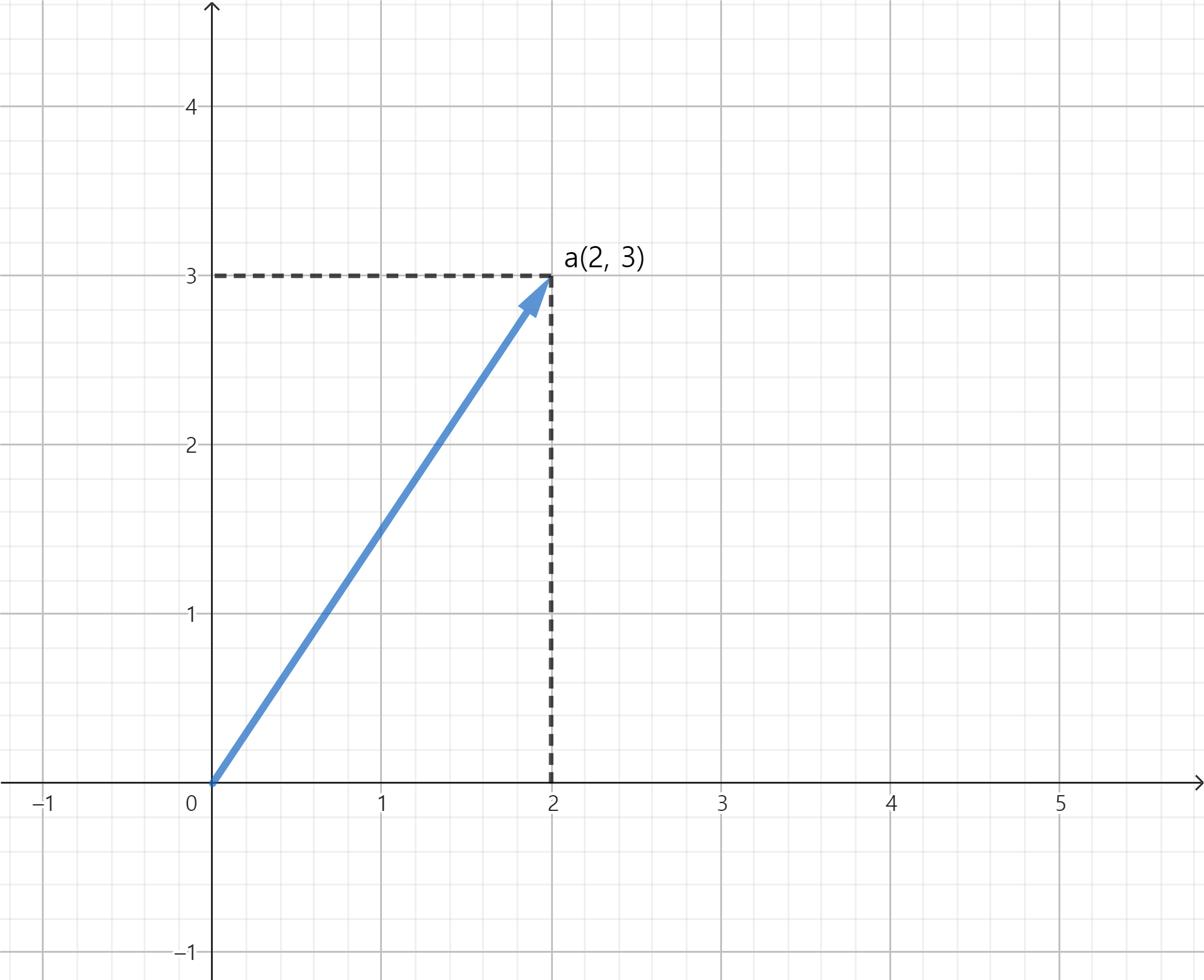
• 가장 흔한 예로는 직각좌표계를 사용함. 한 벡터의 기점을 좌표계의 원점으로 하고 벡터의 종점의 좌표로 해당 벡터를 표시함
  

🔆 벡터의 성분, 분해, 합성

• 벡터의 성분은 각각의 좌표축에 벡터를 투영 시켜(Projection)얻음
• 이 또한 벡터이므로 성분벡터(Component Vector, $a_x, a_y$)라고 부름
• 따라서 $a_x, a_y$는 “벡터 a의 축 성분 벡터” 라고 부름
• 이것은 2차원 이상의 공간에서는 차원의 수 만큼 성분이 존재하며, 차원을 확장하여 적용 가능
• $\text{a} = a_x + a_y$ 로 표현 가능
• 한 벡터를 자신의 성분 벡터들의 합으로 나타내는 것이 벡터의 분해라고 함
  

📖 단위벡터

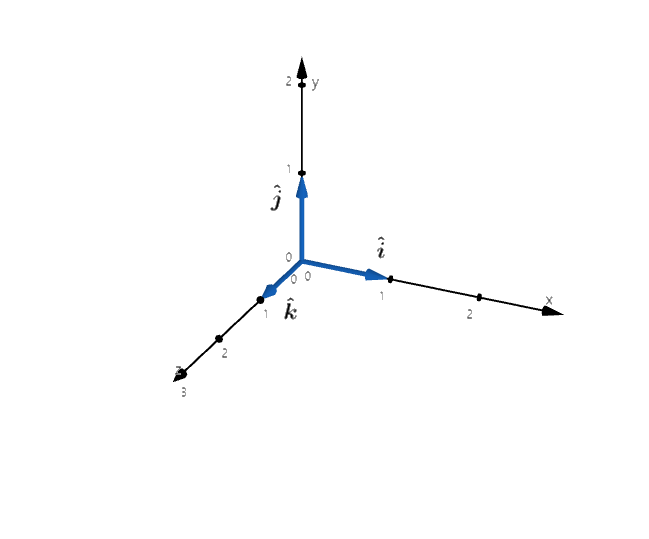
🔆 단위 벡터 - 1

• 벡터의 성분 표시를 편리하게 하기 위해 추가적인 단위 벡터를 도입할 수 있음
• 단위 벡터는 크기가 1 이며, 특정한 방향을 갖는 벡터임. 벡터의 방향을 나타내기 위할 뿐 차원과 단위가 없음
• 3차원 직각좌표계(X, Y, Z)가 주어질 때, 각 좌표축에 나란한 방향을 갖는 단위 벡터를 각각 $\large\color{red}\hat{i},\hat{j},\hat{k}$라고 나타냄
  

🔆 단위 벡터 - 2

• 축의 방향은 오른나사 규칙, 오른손 규칙의 관례를 따라 정한 것
• 모든 좌표 축에 대한 단위 벡터들의 집합 { $\color{red}\hat{i},\hat{j},\hat{k}$ }을 기저 벡터 집합(basis vectors)라고 부름
• 특정 기저벡터 집합을 선택하는 것은 특정한 직각좌표계를 선택하는 것과 동등
  • 직각 좌표계의 축 자체가 기저 벡터 집합
• 스칼라 배(Scalar multiplication)의 정의를 이용하여 벡터 a의 성분 벡터들은 각각 아래와 같이 표현 할 수 있음
  • $\large\text{a}_x= a_x\hat{i}\\\text{a}_y= a_y\hat{j}\\\text{a}_z= a_z\hat{k}$
• 여기서 벡터들과 함께 벡터 공간에 연관된 스칼라인 $a_x, a_y, a_z$를 벡터의 성분이라고 부름
• $\text{a} = a_x\hat{i} +a_y\hat{j} +a_z\hat{k}$ 또는 $\text{a} = (a_x, a_y, a_z)$