선형대수 : 01. 벡터(Vector) - 2 : 벡터의 연산

❇️ 요약

• 벡터의 덧셈
• 벡터의 뺄셈
• 벡터의 곱셈

📖 벡터의 덧셈

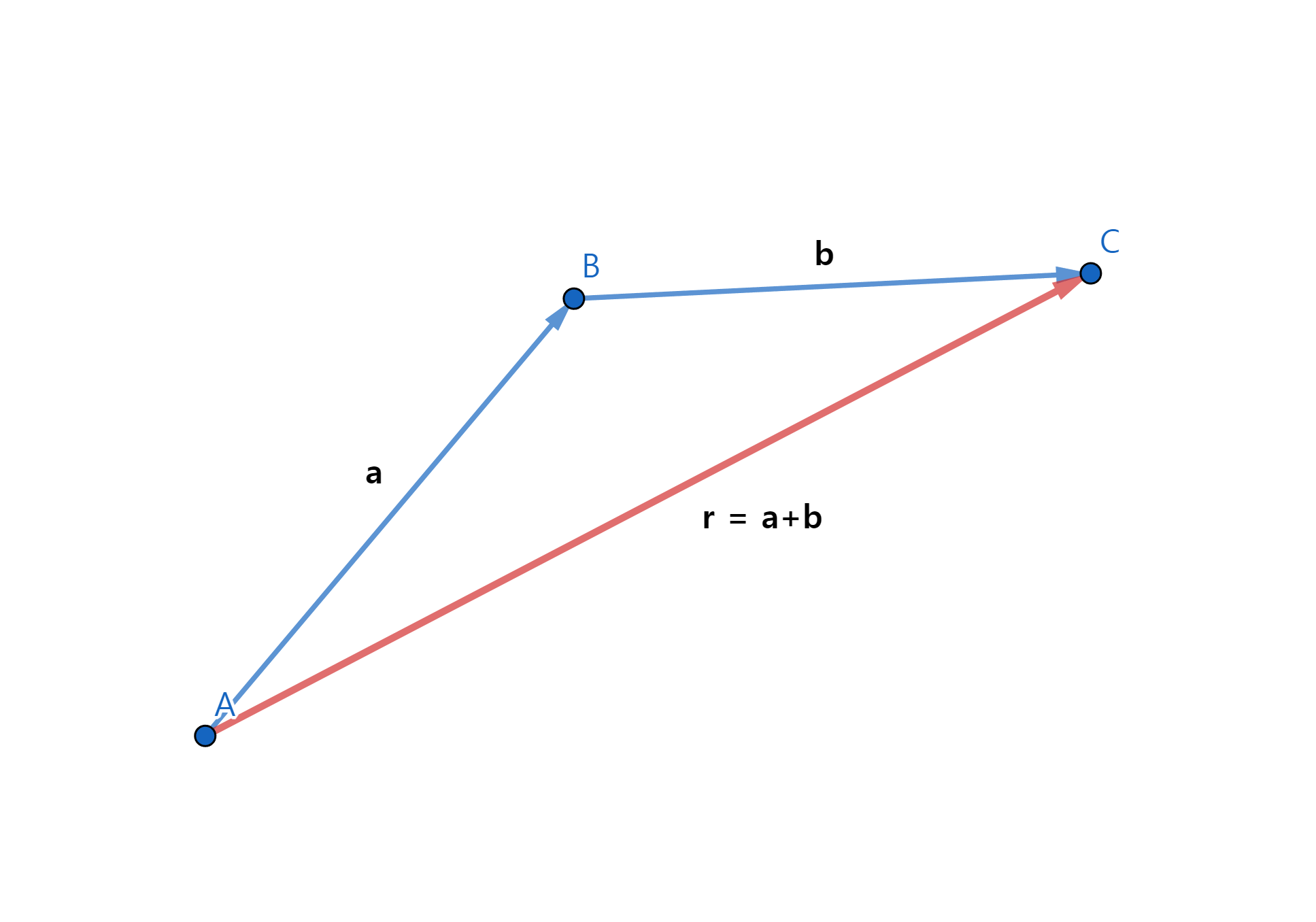
🔆 기하학적인 방법 1 : 삼각형법(Tail-to-tip method)

• 공간 상의 위치는 벡터 량임
• 위치의 변화인 변위(displacement)도 벡터 량임
• r = a + b
  

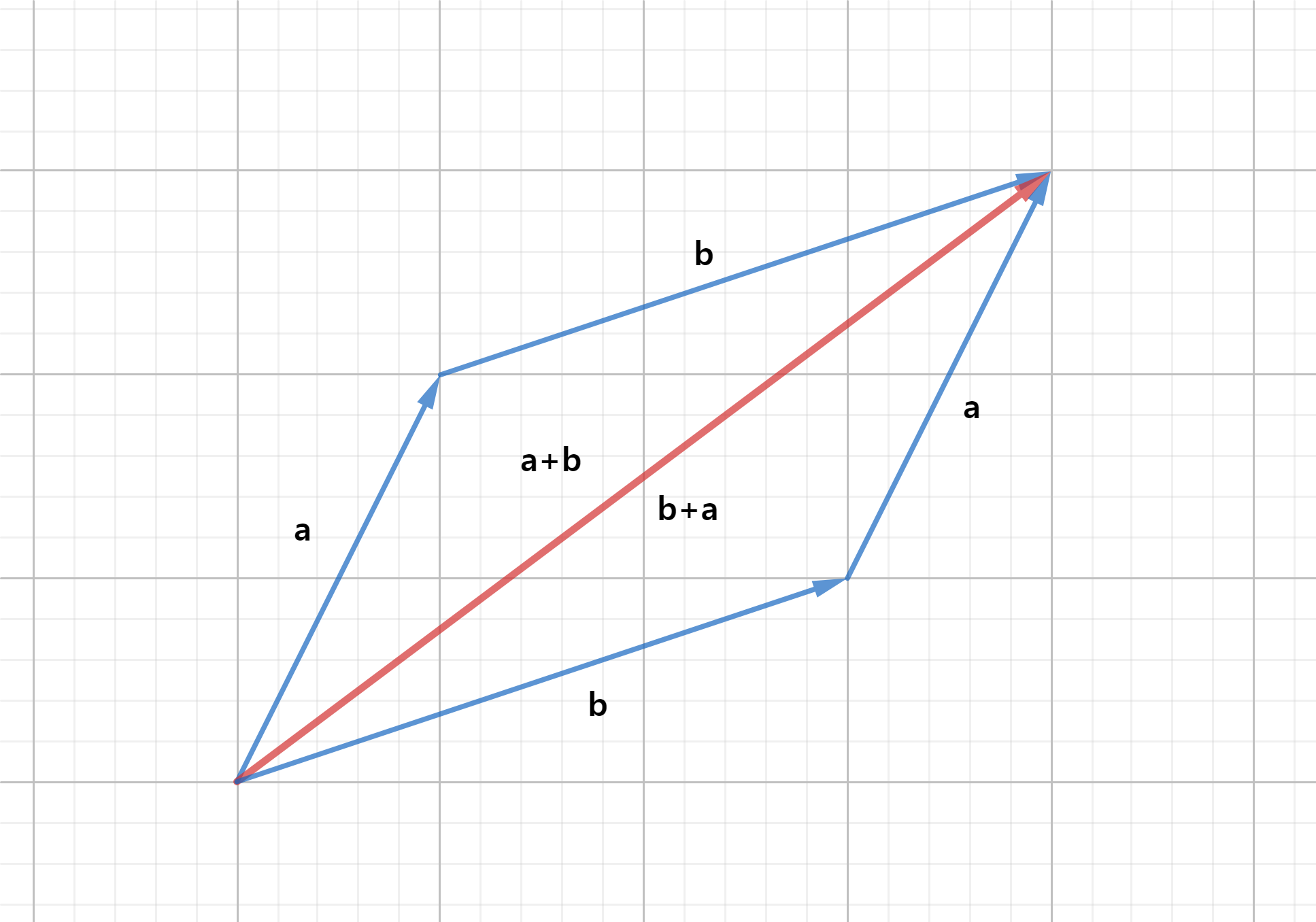
🔆 덧셈의 교환 법칙

• 두 벡터의 순서가 바뀌어도 결과는 마찬가지임
• 이를 벡터의 덧셈이 교환법칙을 만족시킨다라고 말함
• a + b = b + a
  

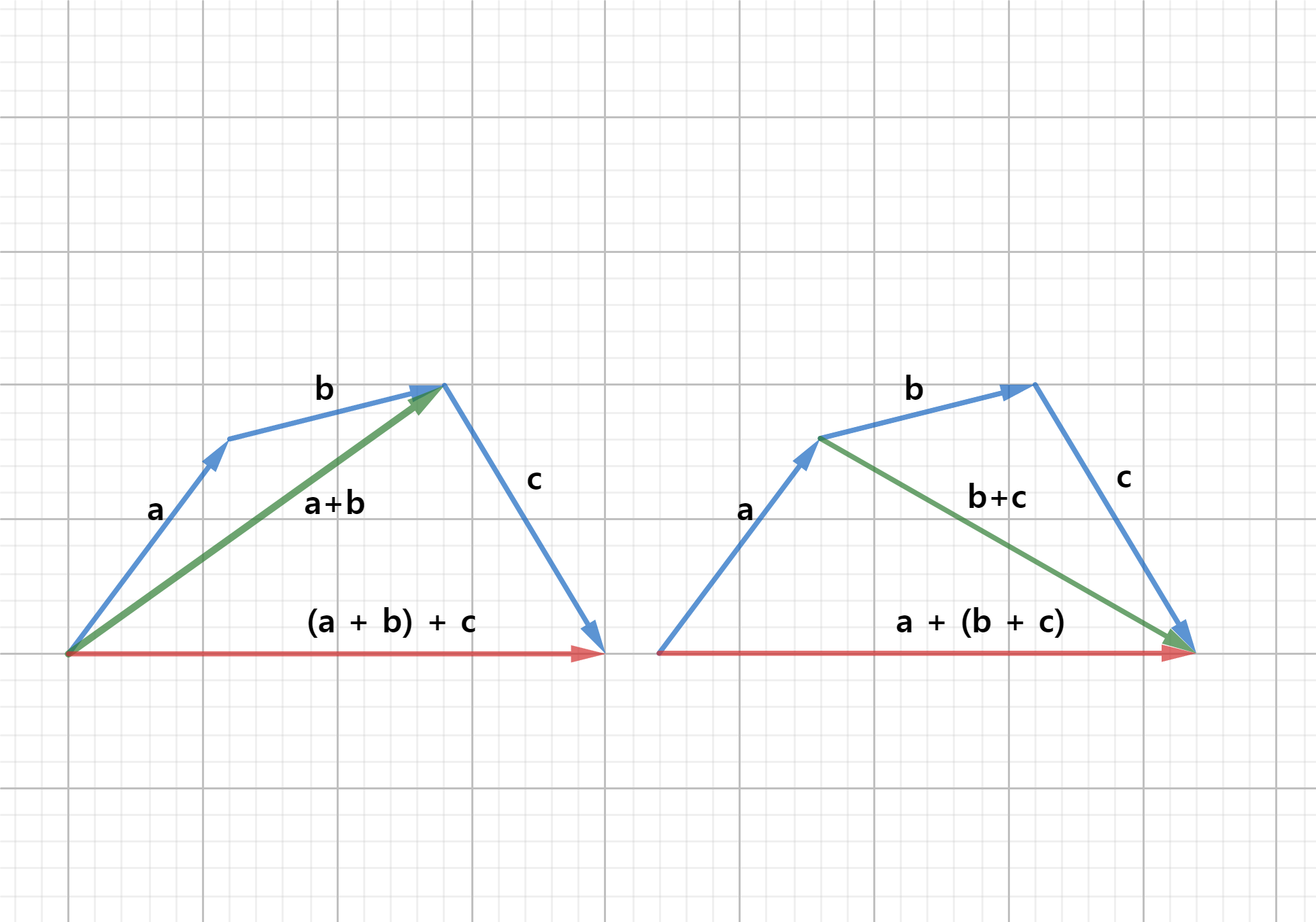
🔆 덧셈의 결합 법칙

• 더하는 벡터들이 두 개 이상인 경우에도, 더하는 순서에 상관없이 결과는 동일함
• 이를 벡터의 덧셈이 결합법칙을 만족시킨다라고 말함
• $\color{red}(a+b)+c = a + (b+c)$
  

🔆 기하학적인 방법 2 : 평행사변형법(Parallelogram method)

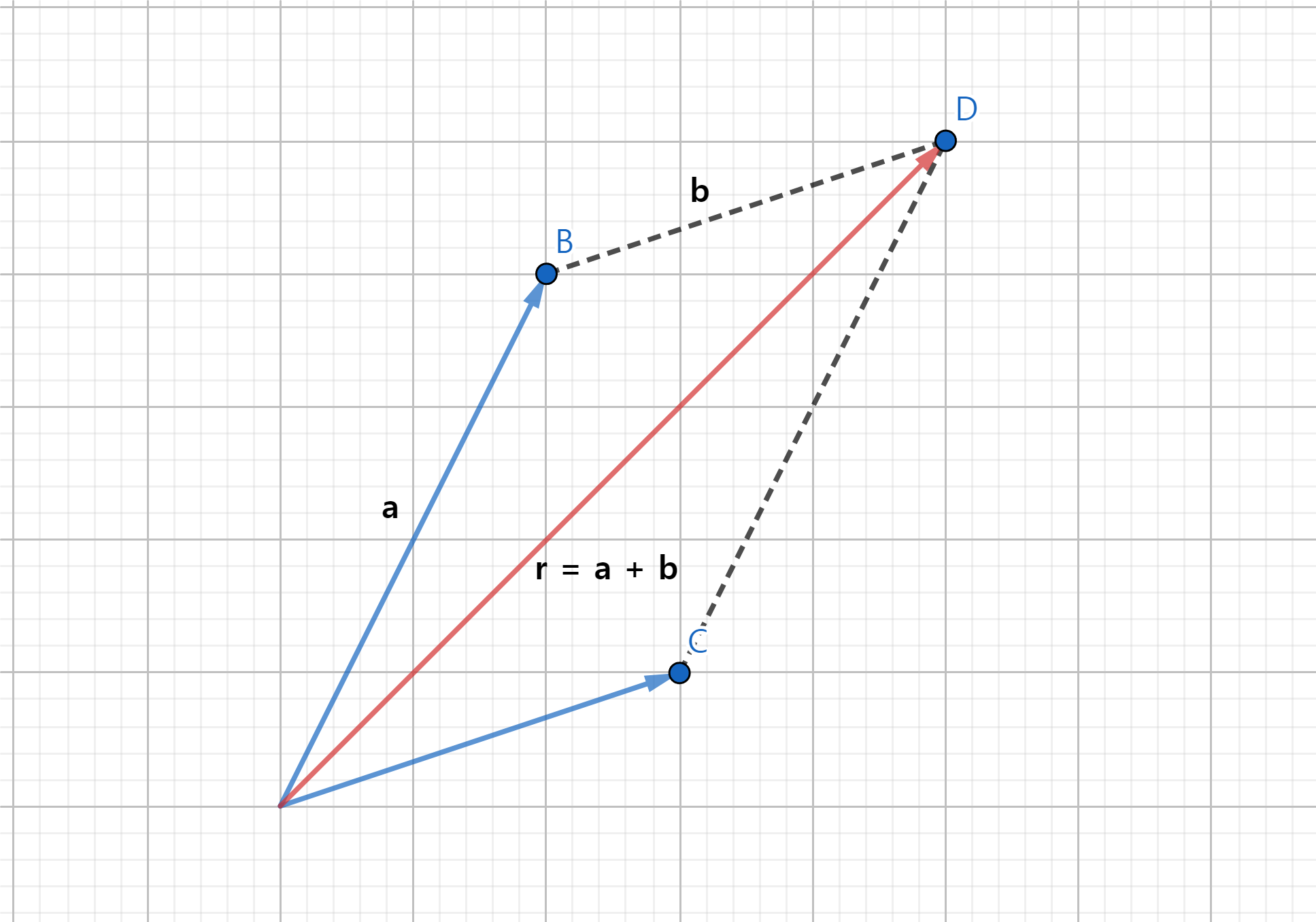
• b를 평행이동하여, a와 b의 꼬리를 일치 시킨 후, 두 벡터를 인접한 두 변으로 평행사변형을 그렸을 때, 두 벡터의 꼬리에서 시작하는 평행사변형의 대각선이 a와 b의 합벡터에 해당됨
• 이것이 삼각형법과 같은 결과를 준다는 사실은 그림으로 입증
  

🔆 성분을 이용한 대수적인 방법

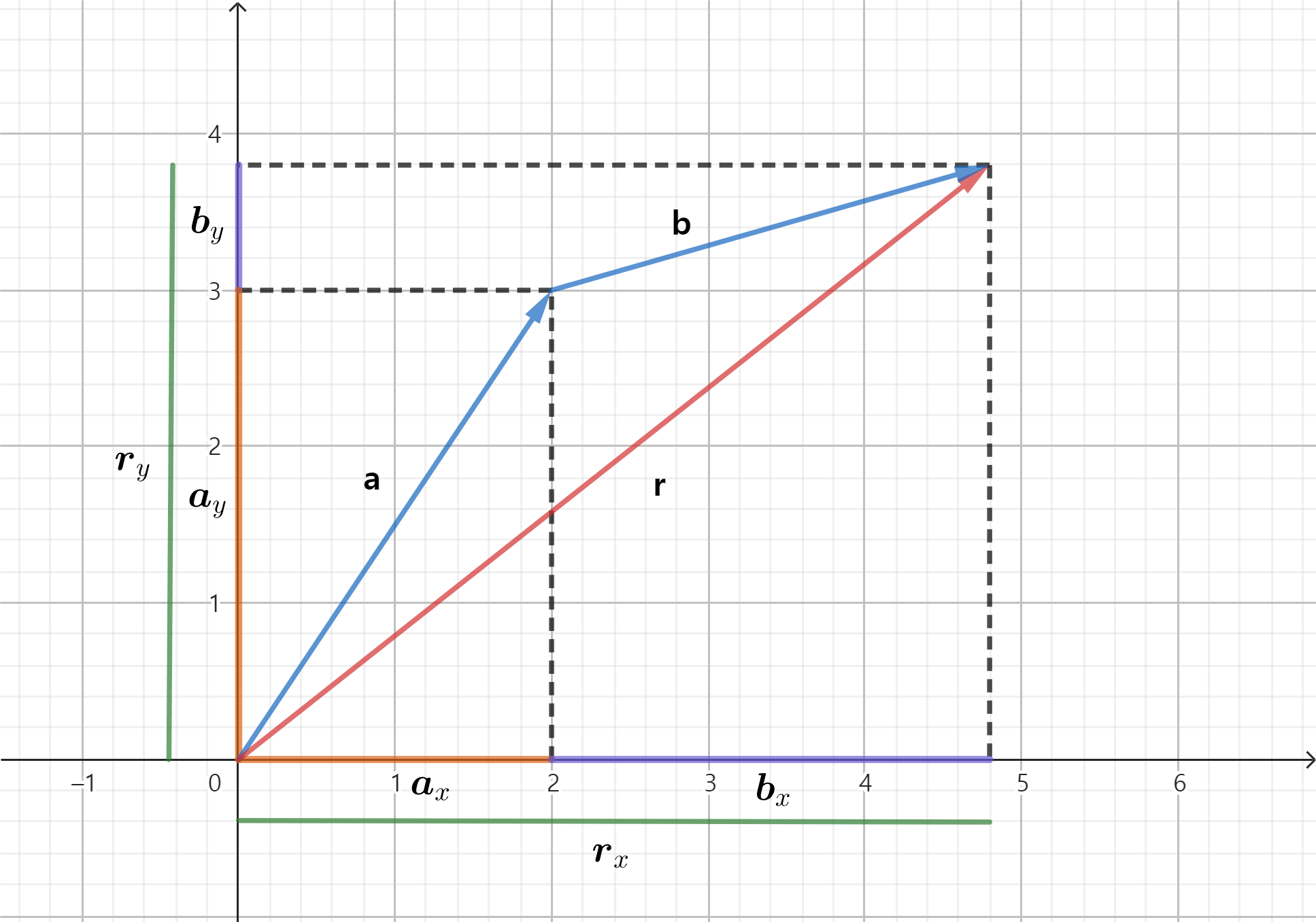
• 두 벡터가 동일하다면 대응하는 벡터의 성분이 반드시 같아야 함
• $\large \color{red}r_x = a_x +b_x \quad r_y = a_y +b_y$

  📌 예시
  a=(2, 3), b=(2.7, 0.7) 일 경우 r=(4.7, 3.7)
  ※ b 벡터를 r 벡터로 잘못 쓰는 경우 조심!

• $\large \text{r} = r_x + r_y$
  

📖 벡터의 뺄셈

🔆 벡터의 뺄셈

• 자기 자신과 크기는 같고, 방향이 정반대인 음벡터의 정의를 이용하면 됨
• 식 $\large\color{red}r=a-b$의 양쪽에 b를 더한 후 결합법칙과 교환법칙을 적용하여 연산의 순서를 정리하면 식 $\large\color{red}a = b+r$을 얻을 수있음
  

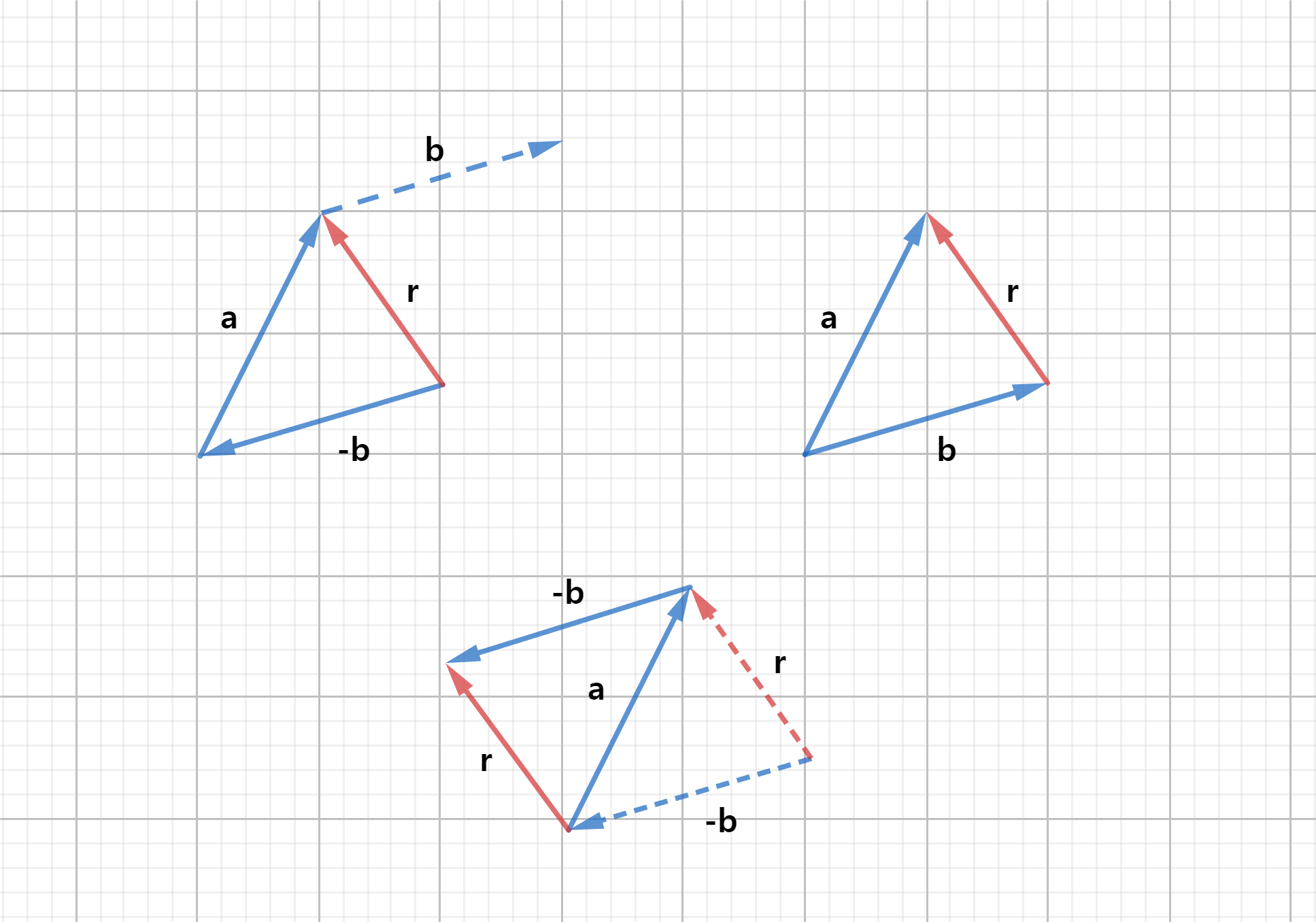
-b의 기점를 a의 종점으로 옮겨 r을 구할수도 있다.

📖 벡터의 곱셈

🔆 벡터의 곱셈

• 내적 | 內積 | inner product ( • )
  • Result : Scalar(크기)
• 외적 | 外積 | outer product ( × )
  • Result : Vector(크기, 방향)

🔆 벡터의 내적-1

• 내적은 벡터를 마치 수처럼 곱하는 개념
• 벡터에는 방향이 있으므로, 방향이 일치하는 만큼만 곱함
  • 예를 들어 두 벡터의 방향이 같으면, 두 벡터의 크기를 그냥 곱함
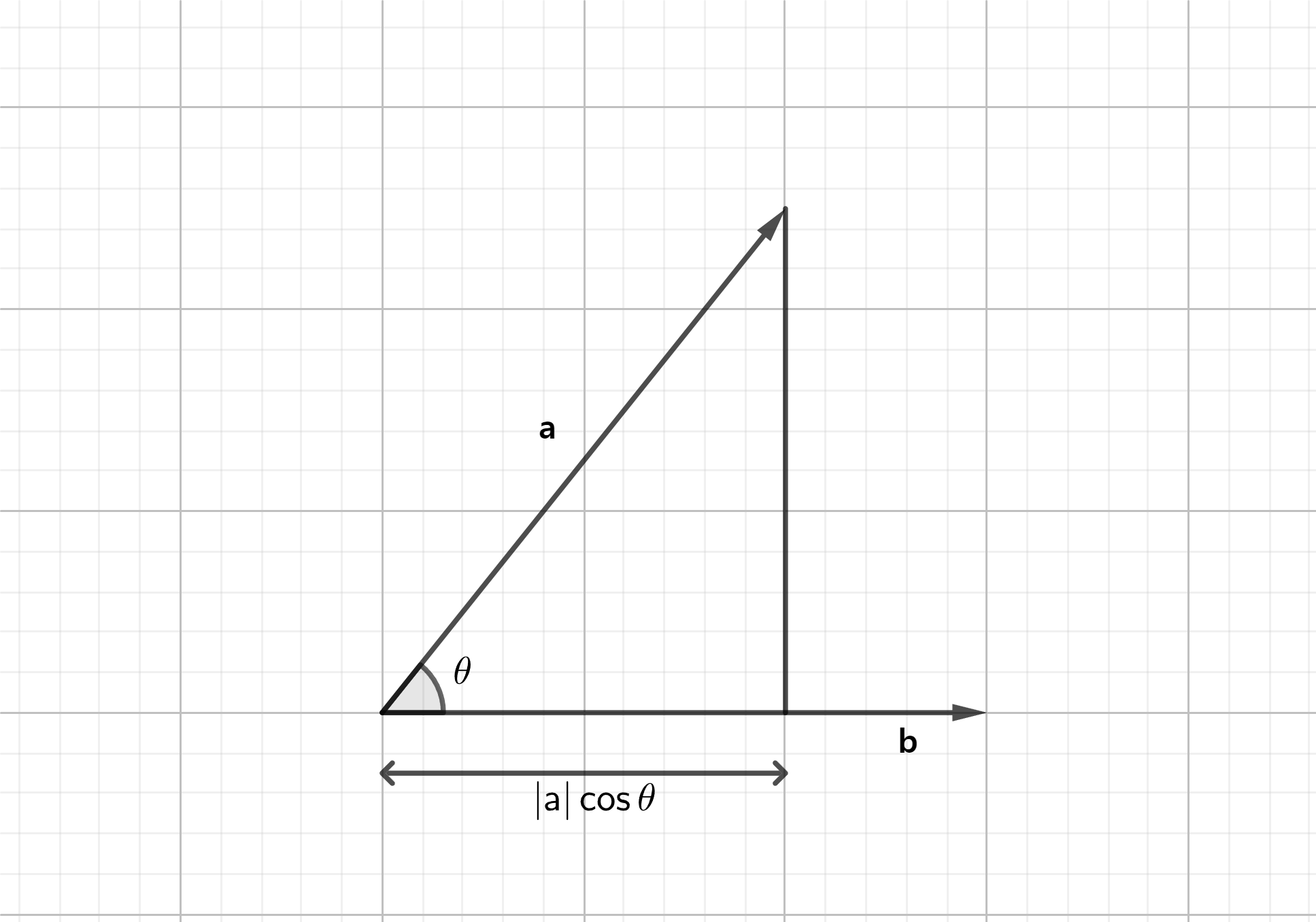
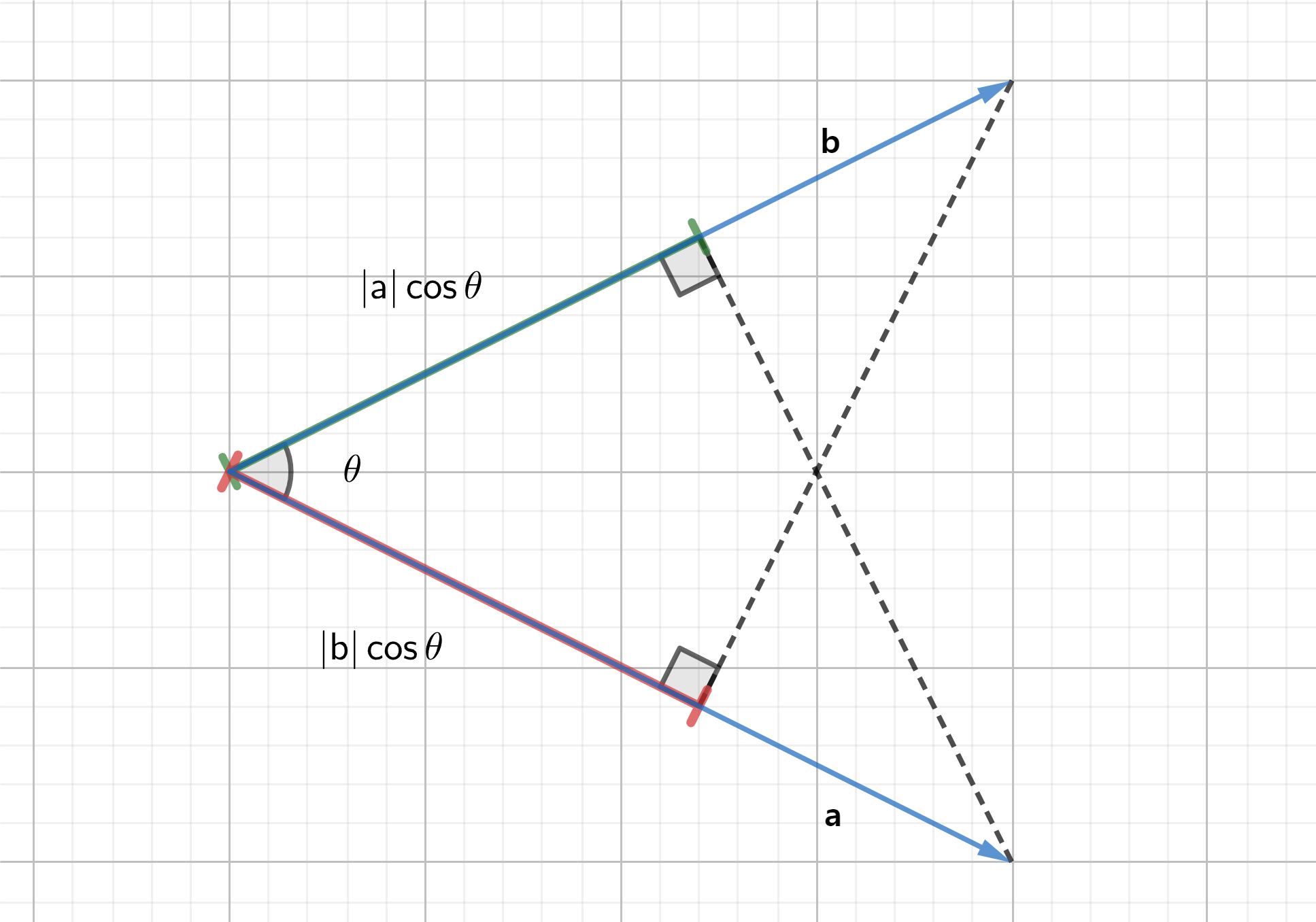
• 두 벡터가 이루는 각이 90도 일 땐, 일치하는 정도가 전혀 없기 때문에 내적의 값은0
• 내적은 한 벡터를 다른 벡터로 투영(Projection), 정사영 시켜서, 그 벡터의 크기를 곱함
• $\large\color{red}\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos\theta$
  

🔆 벡터의 내적-2

• 단위 벡터인 $\large\color{red}\hat{i},\hat{j},\hat{k}$는 곱셈에 사용되지 않고 스칼라 값들만으로 계산을 하게 됨
• Scalar 곱은 한 벡터의 크기에 그 벡터에 투영된 다른 벡터의 크기를 곱한 양으로 간주함
• $\large\color{red}a\cdot b=(a\cos\theta)b\\\qquad= a(b\cos\theta)$
• $\large\color{red}a\cdot b = b\cdot a$ (Scalar곱은 교환법칙 만족)
• $\large\color{red} a\cdot b = (a_x\hat{i}+a_y\hat{j}+a_z\hat{k})\cdot(b_x\hat{i}+b_y\hat{j}+b_z\hat{k})\\ \qquad= a_xb_x+a_yb_y+a_zb_z$

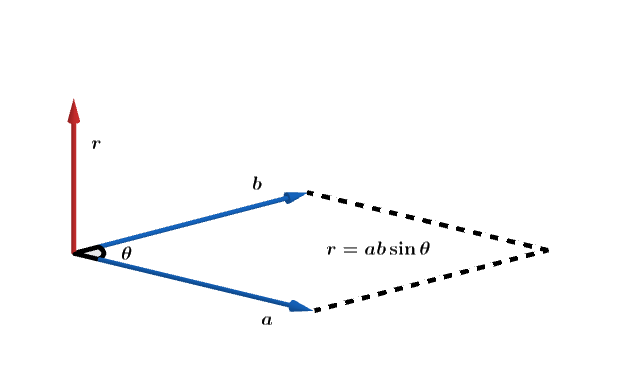
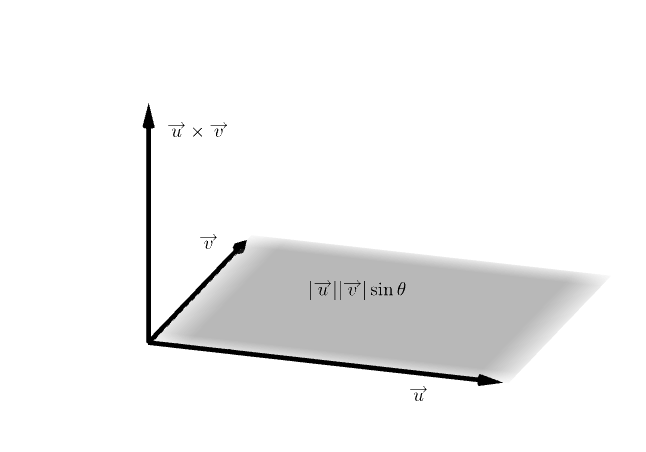
🔆 벡터의 외적-1

• 두 벡터를 곱하는 또다른 정의로 외적이 있음
• 외적의 결과 값은 벡터인데, 방향은 두 벡터 a와 b가 이루는 평면에 수직
• $r= uv \sin\theta$
• $u\times v= -v\times u$
  • 교환, 결합 X
• $\large\color{red}|\overrightarrow{u}\times\overrightarrow{v} | = |\overrightarrow{u}||\overrightarrow{v}|\sin\theta$

🔆 벡터의 외적-2

• 직각좌표계에서 단위 벡터들은 서로 수직하므로, 서로 다른 단위벡터들의 벡터곱은 크기가 1이고 나머지 단위벡터에 나란한 방향임
• 벡터곱과 좌표축의 양의 방향들이 모두 오른손 규칙을 따르므로, 벡터 곱을 취하면 아래와 같음
  • $\large\color{red} \hat{i}\times\hat{j}=\hat{k} \\ \hat{j}\times\hat{k}=\hat{i} \\ \hat{k}\times\hat{i}=\hat{j}$
• 자기 자신과의 벡터곱은 사이각이 0이므로 모두 영임
  • $\large\color{red} \hat{i}\times\hat{i}= \hat{j}\times\hat{j}= \hat{k}\times\hat{k}=0$

🔆 벡터의 외적-3

• $\large\color{red} a\times b = (a_x\hat{i}+a_y\hat{j}+a_z\hat{k})\times(b_x\hat{i}+b_y\hat{j}+b_z\hat{k})\\ \qquad= (a_yb_z-a_zb_y)\hat{i} +(a_zb_x-a_xb_z)\hat{j}+(a_zb_y-a_yb_x)\hat{k}$