선형대수 : 03 선형대수학 - 7 : 고유벡터와 고유값 ⭐

❇️ 요약

• 고유값 - eigenvalue
• 고유벡터 - eigenvector
• 고유공간 - eigenspace

📖 고유값과 고유벡터

중요

$\begin{aligned} A\text{x} =\lambda\text{x}일때, \\\lambda = 고유값, \quad \text{x}=고유벡터\\ \text{위 두값을 가질려면 nontrivial solution(비자명해)가 있어야하고,}\\ \text{그러기 위해서 free variable이 있어야 함} \end{aligned}$

🔆 1. 고유값과 고유벡터의 기본 아이디어

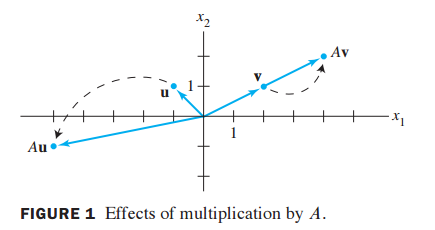
• 행렬 A, u, v가 다음과 같이 주어졌을 때 곱셈 결과를 시각적으로 표현
• $Av$의 결과는 동일한 line에 solution이 존재하도록 결과가 나옴
• 고유값(Eigenvalue)와 고유벡터(Eigenvector)의 기본 idea

🔆 2. 고유벡터 - eigenvector

• 고유벡터의 정의

• $A\text{x} = \lambda \text{x}$를 만족하는 nonzero vector $\text{x}$가 고유벡터(eigenvector)
• 또한, $A\text{x} = \lambda \text{x}$에서 $\text{x}$가 nontrivial solution(비장명해)이 존재할 때 scalar $\lambda$가 고유값(eigenvalue)가 됨
• 여기서 $\text{x}$를 $\lambda$에 상응하는 고유벡터(eigenvector)이라고 함

nontrivial solution(비장명해) :
free variable($\det=0$)를 갖고 있을 때 비자명해를 가지게 됨
free variable이 없으면 unique solution을 갖고, free variable이 있으면 infinitely many solution을 갖음
→평행하면 infinitely many solution → 같은 line 상에 존재하는 것 → 고유벡터와 고유값 계산

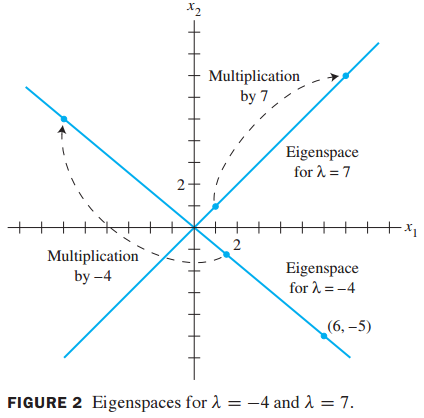
• 예시 1 : 행렬 u와 v가 A의 고유벡터(eigenvector)인지 판단하는 문제
  $A= \begin{bmatrix} 1&6\\ 5&2 \end{bmatrix}, \quad u= \begin{bmatrix} 6\\-5 \end{bmatrix}, \quad v= \begin{bmatrix} 3\\-2 \end{bmatrix}$

  • $A\text{x} = \lambda \text{x}$를 만족하는지 확인하면 됨

    $\begin{aligned} Au&= \begin{bmatrix} 1&6\\ 5&2 \end{bmatrix} \begin{bmatrix} 6\\ -5 \end{bmatrix}= \begin{bmatrix} -24\\ 20 \end{bmatrix}= -4\begin{bmatrix} 6\\ -5 \end{bmatrix}=-4u\\\\ Av&= \begin{bmatrix} 1&6\\ 5&2 \end{bmatrix} \begin{bmatrix} 3\\ -2 \end{bmatrix}= \begin{bmatrix} -9\\ 11 \end{bmatrix}\not=\lambda \begin{bmatrix} 3\\ -2 \end{bmatrix} \end{aligned}$

  • $u$는 $A$의 고유벡터, -4는 $A$의 고유값이 됨

  • $v$는 $A$의 고유벡터가 아님

• 예시 2 : 7이 $A$의 고유값(eigenvalue)인지 파악하고 그에 해당하는 고유벡터(eigenvector)를 찾는 문제
  $A= \begin{bmatrix} 1&6\\ 5&2 \end{bmatrix} \\ A\text{x}=7\text{x}$

  • 위 식을 만족해야 7이 $A$의 고유값(eigenvalue)이 성립함

    $A\text{x}-7\text{x}=0\\ (A-7I)\text{x}=0$

  • 여기서 x는 nonzero vector가 되어야함

    $A-7I= \begin{bmatrix} 1&6\\ 5&2 \end{bmatrix}- \begin{bmatrix} 7&0\\ 0&7 \end{bmatrix}= \begin{bmatrix} -6&6\\ 5&-5 \end{bmatrix}$

  • nontrivial solution을 파악하기 위해 zero vector를 포함한 augmented matrix를 row reduction 후 free variable이 존재하는지 파악하면 됨

    $\begin{bmatrix} -6&6&0\\ 5&-5&0 \end{bmatrix}\sim \begin{bmatrix} 1&-1&0\\ 0&0&0 \end{bmatrix}$

  • $x_2$가 free variable임

  • $x_2$로 표현한 general solution은 다음과 같음

    $x_2\begin{bmatrix} 1\\ 1 \end{bmatrix}$

  • nontrivial solution이 존재하므로 7은 A의 고유값(eigenvalue)이 성립됨

🔆 3. 고유공간 - Eigenspace

• $\lambda$가 $A$의 고유값(eigenvalue)이면 $(A-\lambda I)\text{x}=0$은 nontrivial solution을 가짐
• $\lambda$에 해당하는 A의 고유공간(eigenspace)는 $A-\lambda I$행렬의 null space임
• 고유공간(eigenspace)은 zero vector와 $\lambda$에 해당하는 고유벡터(eigenvectors) 두 가지를 포함
• zero vector는 고유벡터(eigenvector)에 포함되진 않지만 eigenspace에 포함

• 예시문제 : 행렬 A가 다음과 같이 주어졌을때 $\lambda =2$에 해당하는 고유공간(eigenspace)를 찾고 basis를 찾는 문제
  $\begin{aligned} A&= \begin{bmatrix} 4&-1&6\\ 2&1&6\\ 2&-1&8 \end{bmatrix} \\\\ A-2I= \begin{bmatrix} 4&-1&6\\ 2&1&6\\ 2&-1&8 \end{bmatrix}&- \begin{bmatrix} 2&0&0\\ 0&2&0\\ 0&0&2 \end{bmatrix}= \begin{bmatrix} 2&-1&6\\ 2&-1&6\\ 2&-1&6 \end{bmatrix}\\\\ &(A-2I)\text{x}=0 \end{aligned}$

  • homogeneous equation에서 nontrivial solution이 존재하는지 판단하기 위해 augmented matrix를 만들고 row reduction을 통해 free variable이 존재하는지 파악

    $\begin{bmatrix} 2&-1&6&0\\ 2&-1&6&0\\ 2&-1&6&0 \end{bmatrix}\sim \begin{bmatrix} 2&-1&6&0\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix}$

  • x_2, x_3이 free variable임

  • free variable을이용해서 general solution을 표현하면 다음과 같이 됨

    $\begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix}=\begin{bmatrix} 0.5x_2-3x_3\\x_2\\x_3 \end{bmatrix}=x_2 \begin{bmatrix} 1/2\\1\\0 \end{bmatrix}+x_3 \begin{bmatrix} -3\\0\\1 \end{bmatrix}, \quad x_2\text{ and }x_3 \text{ free}$

  • 두 개의 vector는 independent vector이며 고유벡터(eigenvectors)임

  • 두 vector가 independent set이므로 basis는 다음과 같음

    $\begin{Bmatrix} \begin{bmatrix} 1\\2\\0 \end{bmatrix}, \begin{bmatrix} -3\\0\\1 \end{bmatrix} \end{Bmatrix}$

🔆 4. 행렬 A에 의한 곱셈 - Multiplication by A

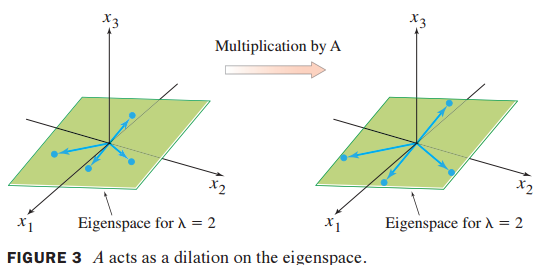
• 3차원 공간에 $\lambda=2$에 대한 고유공간(eigenspace)가 주어졌다고 가정
• 고유공간(eigenspace)는 zero vector와 고유벡터(eigenvectors)를 포함
• 고유공간(eigenspace)에 존재하는 임의의 vector 4개를 선택해서 행렬 A 곱을 하면 크기가 2배씩 늘어나게 됨

🔆 5. 이론 1 - Theorem 1

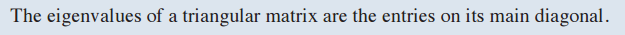
• triangular matrix(삼각행렬)의 고유값(eigenvalues)는 diagonal term(대각행렬)
• 증명

  1. $A$가 upper triangular matrix인 경우

     • $A-\lambda I$는 다음과 같음
     $\begin{aligned} A-\lambda I&= \begin{bmatrix} a_{11}&a_{12}&a_{13}\\ 0&a_{22}&a_{23}\\ 0&0&a_{33} \end{bmatrix}- \begin{bmatrix} \lambda&0&0\\ 0&\lambda&0\\ 0&0&\lambda \end{bmatrix}\\\\ &= \begin{bmatrix} a_{11}-\lambda&a_{12}&a_{13}\\ 0&a_{22}-\lambda&a_{23}\\ 0&0&a_{33}-\lambda \end{bmatrix}\\\\ &(A-\lambda I)\text{x}=0 \end{aligned}$
     • 위 방정식에서 nontrivial solution이 존재해야 함
     • 이는 free variavle이 존재한다는 것을 의미하므로 pivot position이 0이 되어야 함
     • 따라서 $\lambda$는 $a_{11},a_{22},a_{33}$이 될 수 있음
     • $\lambda$의 개수는 n개 이하가 되야하므로 3개 이하가 되어야 함

  2. $A$가 lower triangular matrix인 경우

     • $A$와 $A^T$가 동일한 eigenvalue를 갖고 있다는 것을 증명하면 됨
     • $\lambda I$가 digonal term만 존재하므로 다음의 식이 성립
     $(A-\lambda I)^T=A^T-(\lambda I)^T$
     • $A-\lambda I$는 free variable이 존재하고 lower triangular matrix이므로 det = 0이 되어 not invertible이 됨
     • 역행렬의 성질에 의해 $(A=\lambda I)^T$도 not invertible이 됨
     • 따라서 $(A^T-\lambda I)$도 not invertible이 됨
     • A 행렬을 transpose하여도 diagonal term은 변하지 않으므로 $A$와 $A^T$는 동일한 eigenvalue를 갖게 됨

🔆 6. 고유값이 0

• A의 eigenvalue가 0이면 A는 not invertible
• eigenvector는 nonzero vector이어야 함
• eigenvalue는 0이 되어도 됨
• $A\text{x}=\lambda$에서 $\lambda= 0$ 이면 $A\text{x}=0$인 homogeneous equation이 됨
• 이 homogeneous equation이 nontrivial solution이 존재하면 eigenvector가 존재함
• 따라서  $\lambda= 0$인 경우에도 eigenvector는 존재하게 됨

🔆 7. 이론 2 - Theorem 2

• n×n 행렬 A의 별개의 eigenvalue에 해당하는 eigenvector는 linearly independent set
• 증명

  • {v1,...,vr𝑣1,...,𝑣𝑟}이 linearly dependent이고, v1𝑣1이 nonzero라고 가정

  • linearly dependent sets의 성질에 의해 $v_{p+1}$는 다음과 같이 표현

    $c_1v_1+\cdots+c_pv_p=v_{p+1}$

  • 여기서 A를 곱하면

    $c_1Av_1+\cdots+c_pAv_p=Av_{p+1}$

  • $Av = \lambda v$이므로 아래와 동일하게 표현

    $c_1\lambda_1v_1+\cdots+c_p\lambda_pv_p=\lambda_{p+1}v_{p+1}$

  • 이 두식을 빼면

    $c_1(\lambda_1-\lambda_{p+1})v_1+\cdots+c_p(\lambda_p-\lambda_{p+1})v_p=0$

  • $\lambda$는 distinct이므로 $\lambda_1-\lambda_{p+1}$는 nonzero가 됨

  • 따라서 $c_1, \cdots, c_p$가 무조건 0이 되어야 함

  • 이는 trivial solution밖에 존재하지 않다는 말과 동일

  • 따라서 처음에 linearly dependent로 가정했던 것과 모순이 됨

  • 즉, distinct eigenvalue가 주어지고 그에 해당하는 eigenvector set은 무조건 linearly independent set이 됨