선형대수 : 03 선형대수학 - 6 : 행렬식

yeppi1802·2024년 7월 6일
선형대수제로베이스
0

선형대수_제로베이스 데이터 분석 스쿨

목록 보기
11/12

❇️ 요약

  • 행렬식 - determinant
  • 여인수 - cofactor
  • 여인수 전개 - cofactor expansion
  • 행 연산에 의한 행렬식 변화 - Determinant changes by - row operations
  • det⁡≠0\det ≠ 0
  • det⁡AT=det⁡A\det AT = \det A
  • det⁡AB=(det⁡A)(det⁡B)\det AB = (\det A)(\det B)

📖 행렬식 개요

🔆 계수 - Rank, Pivot, Null space

The rank of a matrix A,denoted by rank A, is the dimension of the column space of A\text{The }\bold{rank}\text{ of a matrix }A,\text{denoted by rank }A,\text{ is the dimension of the column space of }A

  • matrix A의 Rank는 A의 column space의 dimension을 의미

  • column space의 basis vector가 몇 개 존재하는지 알면 그것이 dimension이 됨

  • 예시 문제 - 주어진 행렬의 계수를 구해라

    A=[25−3−4847−4−3969−5240−965−6]A= \begin{bmatrix} 2&5&-3&-4&8\\ 4&7&-4&-3&9\\ 6&9&-5&2&4\\ 0&-9&6&5&-6 \end{bmatrix}

    • A를 row reduction을 통해 echelon form(행사다리꼴)으로 변환하고 pivot column을 찾음

      A∼[25−3−480−325−70−6414−200−965−6]∼⋯∼[25−3−480−325−70004−600000]Pivot columns  _↑_↑_______↑\begin{aligned} A\sim \begin{bmatrix} 2&5&-3&-4&8\\ 0&-3&2&5&-7\\ 0&-6&4&14&-20\\ 0&-9&6&5&-6 \end{bmatrix} \sim\cdots\sim& \begin{bmatrix} \color{tomato}2&5&-3&-4&8\\ 0&\color{tomato}-3&2&5&-7\\ 0&0&0&\color{tomato}4&-6\\ 0&0&0&0&0 \end{bmatrix}\\ \color{blue}\text{Pivot columns}&\;\color{blue}\text{\_}\uparrow\text{\_}\uparrow\text{\_\_\_\_\_\_\_}\uparrow \end{aligned}

    • pivot column 위치의 A의 column이 A의 basis

    • pivot column이 3개 존재하므로 rank A는 3

      추가적으로 null space의 dimension도 구할 수 있음

      free variable이 x3,x5x_3, x_5 2개 이므로 dim Null A = 2

      Null space의 dimension은 free variable의 개수와 같음

🔆 1. 2 × 2 Matirx

  • 2 × 2 행렬에서의 determinant가 nonzero이면 invertible
A=[a11a12a21a22]det⁡A=a11a22−a12a21A= \begin{bmatrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{bmatrix}\\ \det A=a_{11}a_{22}-a_{12}a_{21}

🔆 2. 3 × 3 역행렬이 존재하는 행렬 - 3 x 3 invertible matrix

  • 3 × 3 이상 행렬 부터는 determinant를 구하는 것이 복잡
  • determinant가 0이 아닌 것의 의미는 모든 row에 pivot이 존재한다는 의미
  • row reduction을 진행하고 모든 pivot이 nonzero임을 확인하면 됨
[a11a12a13a11a21a12a22a13a23a11a31a12a32a13a33]∼[a11a12a130a11a22−a12a21a11a23−a13a210a11a32−a12a31a11a33−a13a31]A∼[a11a12a130a11a22−a12a21a11a23−a13a2100a11Δ]\begin{aligned} \begin{bmatrix} a_{11}&a_{12}&a_{13}\\ a_{11}a_{21}&a_{12}a_{22}&a_{13}a_{23}\\ a_{11}a_{31}&a_{12}a_{32}&a_{13}a_{33} \end{bmatrix}\sim\begin{bmatrix} a_{11}&a_{12}&a_{13}\\ 0&a_{11}a_{22}-a_{12}a_{21} &a_{11}a_{23}-a_{13}a_{21} \\0&a_{11}a_{32}-a_{12}a_{31} &a_{11}a_{33}-a_{13}a_{31} \end{bmatrix}\\\\ A\sim\begin{bmatrix} a_{11}&a_{12}&a_{13}\\ 0&a_{11}a_{22}-a_{12}a_{21} &a_{11}a_{23}-a_{13}a_{21} \\0&0 &a_{11}\varDelta \end{bmatrix} \end{aligned}
  • 여기서 Δ\varDelta 는 다음과 같다.
Δ=a11a22a33+a12a23a31+a13a21a32−a11a23a32−a12a21a33−a13a22a31\varDelta=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31}
  • AA가 invertible이므로 Δ\varDelta은 nonzero이여야만 함
  • 2 × 2 matrix에서 determinante는 아래와 같으므로 Δ\varDelta을 다음과 같이 표기 할 수 있음
det⁡A=a11a22−a12a21Δ=a11⋅det⁡[a22a23a32a33]−a12⋅det⁡[a21a23a31a33]+a13⋅det⁡[a22a23a32a33]Δ=a11⋅det⁡A11−a12⋅det⁡A12+a13⋅det⁡A13\begin{aligned} \det A&=a_{11}a_{22}-a_{12}a_{21}\\\\ \varDelta=a_{11}\cdot\det \begin{bmatrix} a_{22}&a_{23}\\ a_{32}&a_{33} \end{bmatrix} &-a_{12}\cdot\det \begin{bmatrix} a_{21}&a_{23}\\ a_{31}&a_{33} \end{bmatrix} +a_{13}\cdot\det \begin{bmatrix} a_{22}&a_{23}\\ a_{32}&a_{33} \end{bmatrix}\\\\ \varDelta=a_{11}\cdot\det A_{11} &-a_{12}\cdot\det A_{12} +a_{13}\cdot\det A_{13} \end{aligned}
  • A13A_{13}은 1th row와 3th column을 제외한 요소들을 의미
A=[1−250204−1310704−20]A=\begin{bmatrix} 1&-2&5&0\\ 2&0&4&-1\\ 3&1&0&7\\ 0&4&-2&0 \end{bmatrix}
  • AA가 위와 같이 주어졌을 때 A32A_{32}은 다음과 같이 표기할 수 있음
[1-250204−1310704−20]\begin{bmatrix} 1&\colorbox{#d4effb}{-2}&5&0\\ 2&\colorbox{#d4effb}0&4&-1\\ \colorbox{#d4effb}3&\colorbox{#d4effb}1&\colorbox{#d4effb}0&\colorbox{#d4effb}7\\ 0&\colorbox{#d4effb}4&-2&0 \end{bmatrix}
  • 3th row와 2th column을 제거하면 아래와 같이 됨
A32=[15024−10−20]A_{32}=\begin{bmatrix} 1&5&0\\ 2&4&-1\\ 0&-2&0 \end{bmatrix}

🔆 3. 행렬식 - Determinant

  • 2 x 2 이상 matrix 일때 determinant 결정 방법은 다음과 같다.

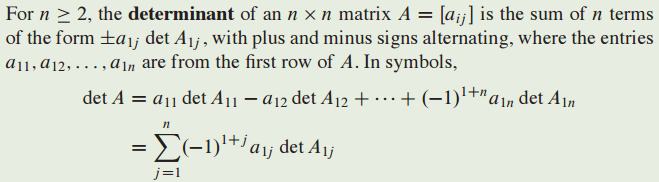
  • determinant의 정의는 다음과 같다.

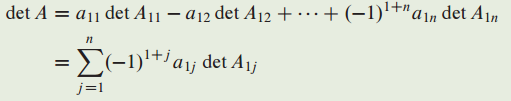
  • 예시문제 : AA 행렬이 주어졌을 때 determinant를 계산하는 문제
A=[15024−10−20]A=\begin{bmatrix} 1&5&0\\ 2&4&-1\\ 0&-2&0 \end{bmatrix}
det⁡A=a11det⁡A11−a12det⁡A12+a13det⁡A13\det A = a_{11}\det A_{11} -a_{12}\det A_{12} +a_{13}\det A_{13}
det⁡A=1⋅det⁡[4−1−20]−5⋅det⁡[2−100]+0⋅det⁡[240−2]=1(0−2)−5(0−0)+0(−4−0)=−2\begin{aligned} \det A&=1\cdot\det \begin{bmatrix} 4&-1\\ -2&0 \end{bmatrix} -5\cdot\det \begin{bmatrix} 2&-1\\ 0&0 \end{bmatrix} +0\cdot\det \begin{bmatrix} 2&4\\ 0&-2 \end{bmatrix}\\ &=1(0-2)-5(0-0)+0(-4-0)=-2 \end{aligned}
  • determinant를 간단히 표현
    • | | 행렬 = def 행렬 표현
det⁡A=1∣4−1−20∣−5∣2−100∣+0∣240−2∣=⋯=−2\det A= 1\begin{vmatrix} 4&-1\\ -2&0 \end{vmatrix} -5\begin{vmatrix} 2&-1\\ 0&0 \end{vmatrix} +0\begin{vmatrix} 2&4\\ 0&-2 \end{vmatrix}=\cdots=-2

🔆 4. 여인수 - Cofactor

  • cofactor를 이용해서 determinant를 여러가지 형태로 표현
  • 이를 여인수 전개(confactor expansion)라고 함
A=[aij],the (i,j)−cofactor of A is the number Cij givenCij=(−1)i+jdet⁡AijA=[a_{ij}], \text{the }\bold{(i,j)-cofactor}\text{ of }A\text{ is the number }C_{ij}\text{ given}\\ C_{ij}=(-1)^{i+j}\det A_{ij}
det⁡A=a11C11+a12C12+⋯+a1nC1n\det A = a_{11}C_{11}+a_{12}C_{12}+\cdots +a_{1n}C_{1n}
  • confactor의 부호는 (−1)i+j(-1)^{i+j}는 다음과 같은 규칙을 가짐
[+−+⋯−+−⋯+−+⋯⋮⋱]\begin{bmatrix} +&-&+&\cdots\\ -&+&-&\cdots\\ +&-&+&\cdots\\ \vdots&&&\ddots \end{bmatrix}

🔆 5. 이론 1 - Theorem 1

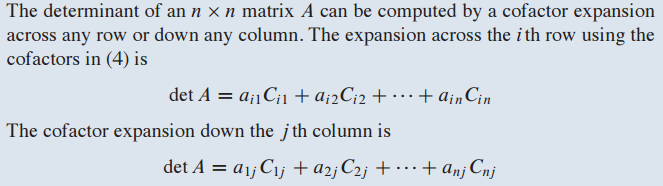
  • cofactor expansion을 이용하면 임의의 row와 column으로 determinant를 표현 가능
  • 어떤 cofactor를 이용하더라도 결과는 동일
  • cofactor를 이용할 때 zero가 많은 row나 column을 기준으로 cofactor expansion을 이용하면 계산이 단순해짐
  • 예시문제 : A가 주어졌을 때 det A를 cofactor expansion을 사용해서 계산하는 문제
A=[15024−10−20]A=\begin{bmatrix} 1&5&0\\ 2&4&-1\\ 0&-2&0 \end{bmatrix}
임의의 row 3 selectdet⁡A=a31C31+a32C32+a33C33=(−1)3+1a31det⁡A31+(−1)3+2a32det⁡A32+(−1)3+3a33det⁡A33=0∣504−1∣−(−2)∣102−1∣+0∣1524∣=0+2(−1)+0=−2\begin{aligned} &\text{임의의 row 3 select}\\ \det A &=a_{31}C_{31}+a_{32}C_{32}+a_{33}C_{33}\\\\ &=(-1)^{3+1}a_{31}\det A_{31}+(-1)^{3+2}a_{32}\det A_{32}+(-1)^{3+3}a_{33}\det A_{33}\\\\ &=0\begin{vmatrix} 5&0\\ 4&-1 \end{vmatrix} -(-2)\begin{vmatrix} 1&0\\ 2&-1 \end{vmatrix} +0\begin{vmatrix} 1&5\\ 2&4 \end{vmatrix} \\\\ &=0+2(-1)+0=-2\\ \end{aligned}
  • 예시문제 2 : 0이 많이 구성되어 있는 matrix는 다음과 같이 cofactor expansion을 사용 가능
A=[3−789−602−573001500024−1000−20]A=\begin{bmatrix} 3&-7&8&9&-6\\ 0&2&-5&7&3\\ 0&0&1&5&0\\ 0&0&2&4&-1\\ 0&0&0&-2&0 \end{bmatrix}
  • first column에 0이 제일 많으므로 이를 기준으로 cofactor expansion을 사용
A=[15024−10−20]A=\begin{bmatrix} 1&5&0\\ 2&4&-1\\ 0&-2&0 \end{bmatrix}
  • first column에 0이 제일 많으므로 이를 이용
det⁡A=3⋅2⋅∣15024−10−20∣det⁡A=3⋅2⋅(−2)=−12\det A = 3\cdot2\cdot \begin{vmatrix} 1&5&0\\ 2&4&-1\\ 0&-2&0 \end{vmatrix}\\ \det A = 3\cdot2\cdot(-2)=-12
  • 0이 많은 row나 column을 이용하면 cofactor expansion을 유용하게 이용할 수 있음

🔆 6. 이론 2 - Theorem 2

  • A가 삼각 행렬(triangular matrix)이면 det A는 A의 digonal term을 곱한 것
  • det⁡A=a11a22a33\det A = a_{11}a_{22}a_{33}
(a1100a21a220a31a32a33):Lower triangular matrix(a11a12a130a22a2300a33):Upper triangular matrix\begin{aligned} \begin{pmatrix} a_{11}&0&0\\ a_{21}&a_{22}&0\\ a_{31}&a_{32}&a_{33} \end{pmatrix} &:\text{Lower triangular matrix}\\\\ \begin{pmatrix} a_{11}&a_{12}&a_{13}\\ 0&a_{22}&a_{23}\\ 0&0&a_{33} \end{pmatrix} &:\text{Upper triangular matrix}\\ \end{aligned}

🔆 7. det EA = (det E)(det A)

  • EE는 기본 행렬(elementary matirx)를 의미
  • det⁡EA\det EA 는 (det⁡E)(det⁡A)(\det E)(\det A)와 동일
E1=[0110]E2=[100k]E3=[1k01]E4=[10k1]A=[abcd]E_1=\begin{bmatrix} 0&1\\ 1&0 \end{bmatrix}\quad E_2=\begin{bmatrix} 1&0\\ 0&k \end{bmatrix}\quad E_3=\begin{bmatrix} 1&k\\ 0&1 \end{bmatrix}\quad E_4=\begin{bmatrix} 1&0\\ k&1 \end{bmatrix}\quad A=\begin{bmatrix} a&b\\ c&d \end{bmatrix}\quad
  • E1E_1은 interchange
  • E2E_2는 second row k scaling
  • E3E_3은 second row에 k scaling한 것을 first row에 더한 replacement
  • E4E_4는 first row에 k scaling 한 것을 second row에 더한 replacement를 의미
  • 각 det⁡\det은 다음과 같다
∣E1∣=−1∣E1∣=k∣E1∣=1∣E1∣=1∣A∣=ad−bc|E_1|= -1 \quad |E_1|= k \quad |E_1|= 1 \quad |E_1|= 1 \quad |A|= ad-bc \quad
  • det⁡EA=(det⁡E)(det⁡A)\det EA = (\det E)(\det A)를 증명하는 과정
∣E1A∣=∣cdab∣=−(ad−bc)=−∣A∣=∣E1∣∣A∣∣E2A∣=∣abkckd∣=(kad−kbc)=k∣A∣=∣E2∣∣A∣∣E3A∣=∣a+kcb+kdcd∣=(ad+kcd−bc−kcd)=∣A∣=∣E3∣∣A∣∣E4A∣=∣abc+kad+kb∣=(ad+kab−bc−kab)=∣A∣=∣E4∣∣A∣\begin{aligned} |E_1A|&= \begin{vmatrix} c & d \\ a & b \end{vmatrix} =-(ad-bc)=-|A|=|E_1||A|\\\\ |E_2A|&= \begin{vmatrix} a & b \\ kc & kd \end{vmatrix} =(kad-kbc)=k|A|=|E_2||A|\\\\ |E_3A|&= \begin{vmatrix} a+kc & b+kd \\ c & d \end{vmatrix} =(ad+kcd-bc-kcd)=|A|=|E_3||A|\\\\ |E_4A|&= \begin{vmatrix} a & b \\ c+ka & d+kb \end{vmatrix} =(ad+kab-bc-kab)=|A|=|E_4||A| \end{aligned}

🔆 8. 수치적인 메모 - Numerical Note

  • cofactor expansion이 복잡하다는 내용
  • cofactor expansion으로 det⁡\det를 구하는 연산은 n!n!이 소요되므로
  • det⁡\det를 cofactor expansion으로 계산하는 것은 멍청한 짓이라는 말로 해석 가능

📖 행렬식 성질

🔆 1. 이론 3. 행 연산 - Theorem 3. Row Operations

  • a. A의 하나의 row 곱이 다른 row에 더해져 B 행렬이 만들어지면 det⁡B=det⁡A\det B = \det A
    • 이는 row replacement를 의미
  • b. B를 만들기 위해 A의 두개의 row가 interchange 됐으면 det⁡B=−det⁡A\det B = -\det A
  • c. A의 하나의 row에 k가 곱해져 B가 만들어졌으면 det⁡B=kdet⁡A\det B = k \det A
    • scaling을 의미
  • 이 세가지 성질을 이용해서 row reduction을 통해 echlon form을 만든 후 cofactor expansion을 이용하면 det를 쉽게 구할 수 있습니다.
  • det⁡EA=(det⁡E)(det⁡A)\det EA = (\det E)(\det A)와 det⁡E=1,−1,k\det E = 1, -1, k
  • BB는 AA 행렬에 row reduction을 사용하여 만들어진 echelon form(행사다리꼴)이라고 가정하면 B=EAB = EA로 표현
  • 각각의 row operation은 두 개의 row에 영향을 끼치므로 영향을 받지 않은 row를 기준으로 cofactor expansion을 사용하면 det⁡A\det A를 쉽게 구할 수 있다.
det⁡EA=ai1(−1)i+1det⁡Bi1+⋯+ain(−1)i+ndet⁡Bin=αai1(−1)i+1det⁡Ai1+⋯+αain(−1)i+ndet⁡Ain=α⋅det⁡A\begin{aligned} \det EA&=a_{i1}(-1)^{i+1}\det B_{i1}+\cdots+a_{in}(-1)^{i+n}\det B_{in}\\\\ &=\alpha a_{i1}(-1)^{i+1}\det A_{i1}+\cdots+\alpha a_{in}(-1)^{i+n}\det A_{in}\\\\ &=\alpha\cdot\det A \end{aligned}
  • 예시
A=[2−8683−9510−301−21−406]A=\begin{bmatrix} 2&-8&6&8\\ 3&-9&5&10\\ -3&0&1&-2\\ 1&-4&0&6 \end{bmatrix}
  • row reduction을 사용하여 echelon form으로 변환하면 det A를 쉽게 구할 수 있음
det⁡A=2∣1−4343−9510−301−21−406∣=2∣1−43403−4−20−12101000−32∣\det A = 2 \begin{vmatrix} 1&-4&3&4\\ 3&-9&5&10\\ -3&0&1&-2\\ 1&-4&0&6 \end{vmatrix}=2 \begin{vmatrix} 1&-4&3&4\\ 0&3&-4&-2\\ 0&-12&10&10\\ 0&0&-3&2 \end{vmatrix}
det⁡A=2∣1−43403−4−200−6200−32∣\det A = 2 \begin{vmatrix} 1&-4&3&4\\ 0&3&-4&-2\\ 0&0&-6&2\\ 0&0&-3&2 \end{vmatrix}
det⁡A=2∣1−43403−4−200−620001∣=2⋅(1)(3)(−6)(1)=−36\det A = 2 \begin{vmatrix} 1&-4&3&4\\ 0&3&-4&-2\\ 0&0&-6&2\\ 0&0&0&1 \end{vmatrix}=2\cdot(1)(3)(-6)(1)=-36

  • echelon form(행사다리꼴)은 triangular matrix이므로 각각의 diagonal term을 곱하면 det을 구할 수 있음

  • 이는 echelon form에서 각각의 pivot들의 곱을 의미

  • row operation 성질을 이용해서 elementary matrix의 det⁡\det를 곱하면 det⁡A\det A가 나오게 됨

  • 간단하게 정리

det⁡A={(−1)r⋅(product ofpivot in U)when A is invertible0when A is not invertible\det A = \begin{cases} (-1)^r\cdot \begin{pmatrix} \text{product of}\\ \text{pivot in }U \end{pmatrix} &\text{when }A \text{ is invertible} \\ 0 &\text{when }A \text{ is not invertible} \end{cases}
  • A가 not invertible이면 pivot이 0인 row가 존재하게 되어 pivot들의 곱이 0이 되게 됨. 따라서 det⁡A=0\det A = 0

🔆 2. 수치적인 메모 - Numerical notes

  • cofactor expansion을 사용해서 determinant를 구하면 n!n!의 연산이 필요
  • 하지만 row operation을 이용하면 방법은 2n3/32n^3/3의 연산이 필요하므로 25 x 25이상의 행렬도 빠르게 계산 가능

🔆 3. 이론 4. - Theorem 4

  • det⁡A=0\det A = 0이 아니면 A는 invertible
  • A가 not invertible이면 det⁡A=0\det A = 0
  • A가 다음과 같이 주어졌을 때 det⁡A=0\det A = 0이 나오므로 A는 not invertible matrix
A=[3−12−505−3−6−67−74−5−809]A=\begin{bmatrix} 3&-1&2&-5\\ 0&5&-3&-6\\ -6&7&-7&4\\ -5&-8&0&9 \end{bmatrix}
det⁡A=det⁡[3−12−505−3−605−3−6−5−809]=0\det A=\det\begin{bmatrix} 3&-1&2&-5\\ \color{tomato}0&\color{tomato}5&\color{tomato}-3&\color{tomato}-6\\ \color{tomato}0&\color{tomato}5&\color{tomato}-3&\color{tomato}-6\\ -5&-8&0&9 \end{bmatrix}=0

🔆 4. 이론 5 - Theorem 5

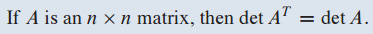
  • ATA^T의 det과 det A는 동일

🔆 5. 이론 6. 곱셈의 성질 - Multiplicative Property

  • det⁡AB=(det⁡A)(det⁡B)\det AB = (\det A)(\det B)
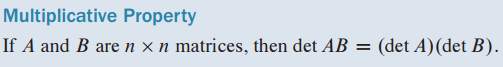
  • A와 B가 다음과 같이 주어졌을 때 det⁡AB=(det⁡A)(det⁡B)\det AB = (\det A)(\det B)가 성립하는지 확인
A=[6132]  and  B=[4312]A=\begin{bmatrix} 6&1\\ 3&2 \end{bmatrix} \;\text{and}\; B=\begin{bmatrix} 4&3\\1&2 \end{bmatrix}
AB=[6132][4312]=[25201413]det⁡AB=25⋅13−20⋅12=325−280=45(det⁡A)(det⁡B)=9⋅5=45=det⁡AB\begin{aligned} AB&=\begin{bmatrix} 6&1\\ 3&2 \end{bmatrix} \begin{bmatrix} 4&3\\1&2 \end{bmatrix}= \begin{bmatrix} 25&20\\14&13 \end{bmatrix}\\\\ \det AB&=25\cdot13-20\cdot12=325-280=45\\\\ &(\det A)(\det B)=9\cdot5=45=\det AB \end{aligned}
  • ❗주의. det(A + B)는 det A + det B와 동일하지 않다.
profile
yeppi1802
제로베이스 DA7 김예빈입니다.
이전 포스트

선형대수 : 03 선형대수학 - 5 : LU 분해(LU decomposition)⭐

다음 포스트

선형대수 : 03 선형대수학 - 7 : 고유벡터와 고유값 ⭐

0개의 댓글