INDEX

• part1
  • greates common divisor
  • (extended) Euclid's Algorithm
  • Modular Arithmetic
  • Euler's Totient Function
  • Fermat's Theorem
  • Euler's Theorem
• part2
  • randomness
  • true random nubmer
  • pseudo-random number
  • cryptographic pseudo-random number

prime number

prime number

• prime number = 소수 = only have divisors of 1 and self

  • cannot be written as a product of other number
  • 1 is prime, but is generally not of interest

• Prime Factorization
  : All numbers can be expressed as a unique products of primes. (모든 수는 prime num들의 곱으로 표현될 수 있다)
  n = a X b X c

  • ex) 10 = 25 , 20 = 22*5
  • factoring a number is relatively hard!

• relatively prime numbers
  • a와 b가 common divisor가 1을 제외하고 없을때, a와 b는 relatively prime이다

GCD

• greatest common divisor

• by comparing their prime factorizations & using the least common powers(가장 큰 공약수) -> we can determine the GCD

  • ex) gcd(273, 399)
    273 = 3*7*13, 399 = 3*7*19.
    gcd(273, 399) = 3*7=21

• Euclid Algorithm
  gcd를 구할 수 있다!

  • 수도코드

  def Euclid_GCD(a,b) :
  # Assume a and b are nonnegative integers
  if (b==0) :
    gcd(a,b) = a # stopping condition
  else 
    gcd(a,b) = gcd(b, a%b) # recursive step

  • 예시
    a = 54, b = 30.
    gcd(54, 30) = gcd(30, 54%30) = gcd(30, 24)
    gcd(30, 24) = gcd(24, 30%24) = gcd(24, 6)
    gcd(24, 6) = gcd(6, 24%6) = gcd(6,0)
    gcd(6,0) = 6
    ==> GCD는 6이다!

• Extended Euclidean Algorithm
  $a\times x +b\times y = gcd(a,b)$
  정수 a,b가 주어질때, 중간과정의 x와 y도 알 수 있다!

  • 예시1
    

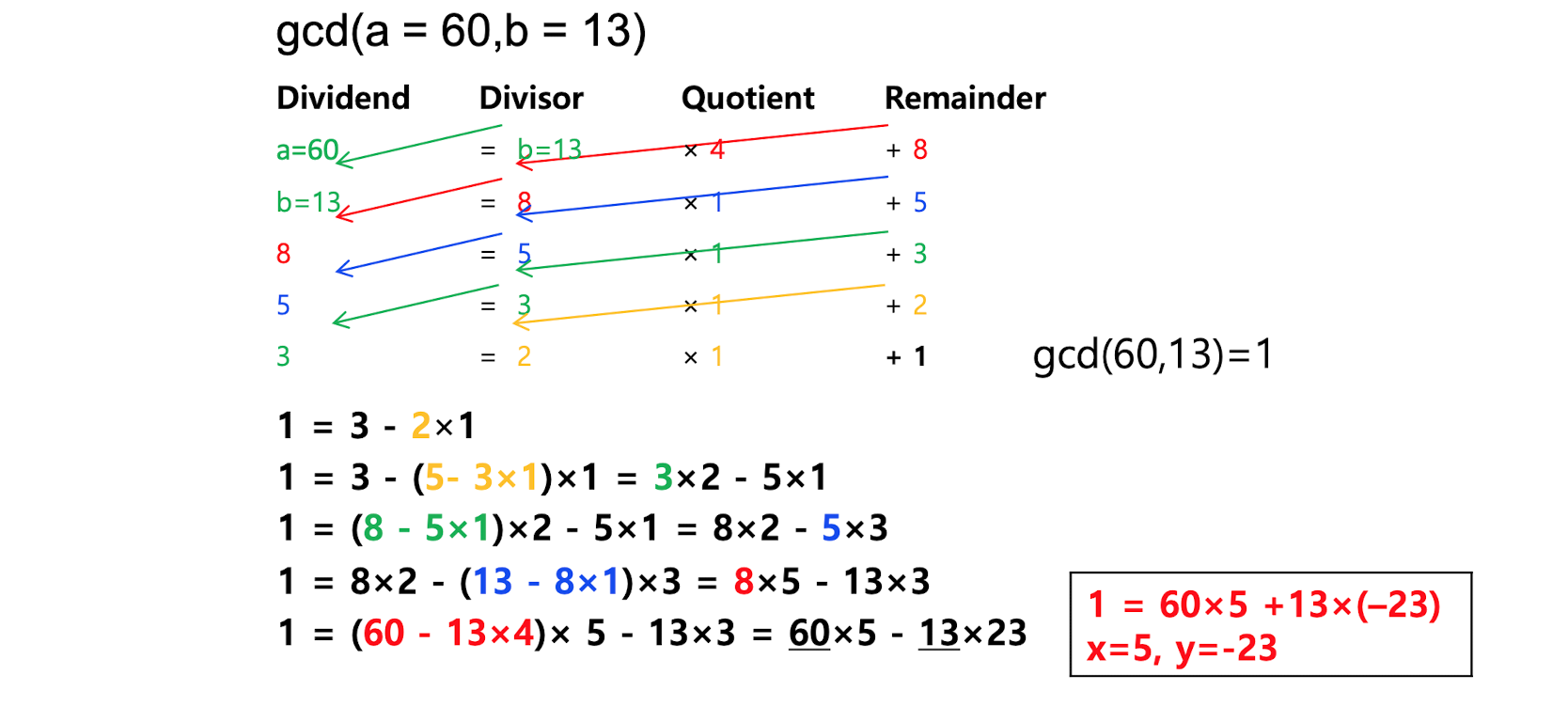
  • 예시 2
    

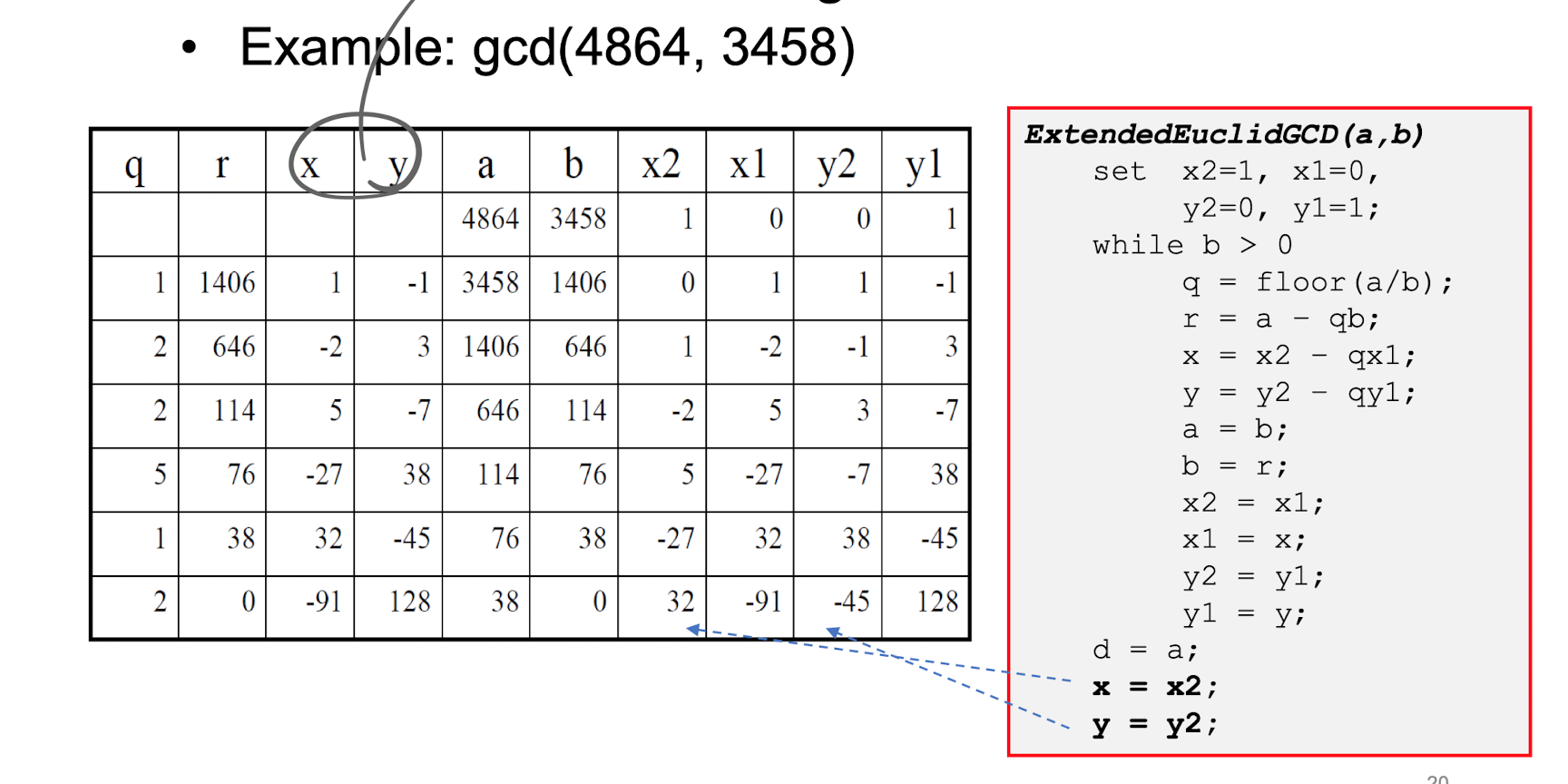
Modular Arithmetic

나머지 연산

• 용어정리

  • congruence
    modular 연산후 같은 remainder 가질때
    ex) 100 mod 11 = 34 mod 11 = 1
  • Residue
    a mod n = b 혹은 a = qn + b 일때 b
    보통 가장 작은 정수를 고름

• ⚠️Properties⚠️
  a = b (mod n) and c = d (mod n) 일때,

  • a + c = b + d (mod n)
  • ac = bd (mod n)
  • a = b(mod n) $\rightarrow a^k = b^k$(mod n)
  • a + kn = b(mod n)

• relatively prime한 두 수 a, b가 있을때
  $aa^i = 1(mod b)$인 $a^i$가 존재한다.

  • $a^i$는 Extended Euclidean algorithm으로 계산가능
  • 

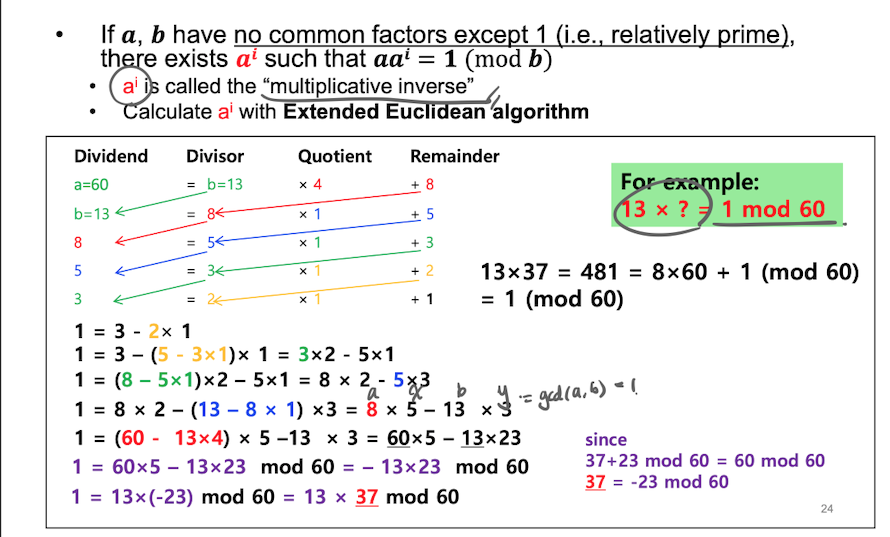
Euler Totient Fucntion

• residues

  • complete residue : 모든 residue
  • reduced residue : n과 relative prime인 residue
    • ex) n = 10일때
      complete set of residues = {0, 1, 2, 3, 4, 5, 6,7, 8, 9}
      reduced set of residues = {1, 3, 7, 9}

• Euler Totient Function $\varphi (n)$
  reduced set of residues의 원소 갯수
  ex) $\varphi(10) = 4$ (1, 3, 7, 9)
  -> n=pq이고, p,q는 prime일때, n보다 작은 n에 대해 relatively prime인 양수의 갯수를 구할 수 있다.
  p가 prime -> $\varphi(p) =p -1$
  p,q가 prime-> $\varphi(pq)=(p-1)\times (q-1)$

  • ex) $\varphi(37)$ = 37-1 = 36
    $\varphi(11)$ = 11-1 = 10
    $\varphi(21)$ = (3-1)*(7-1)=2*6=12
    $\varphi(10)$ = (2-1)*(5-1)=1*4=4
    

• Fermat's Little Theorem
  $a^{p-1}=1$(mod $p$)
  where $p$ is prime and gcd(a, p) = 1
  (p는 Prime이고, a,p는 relatively prime일때)

  • ex
    $4^6$mod 7 = 1
    $19^{22}$mod 23 = 1

    Fermat's Little Theorem 응용
    매우 큰 수 p에 대해, $a^{p-1}=1$(mod $p$) 이까
    - $a^p$ mod $p=a$
    - $a^{(p-1)\times k+1}$mod $p$ = a

  • ex
    $4^{37}$mod 7 = $4^{6\times 6+1}$mod 7 = $1^6 \times$ 4 mod 7 = 4
    $19^{22\times 2+1}$ mod 23 = $(19^{22})^2\times$ mod 23 = 19
    $89^{100\times10 + 1}$ mod 101 = $(89^{100})^{10}\times$89 mod 101 = 89

• Euler's Theorem
  $\varphi (n)$이 Euler's Totient function 이고,
  gcd(a,n) = 1 이면
  $a^{\varphi(n)}=1$(mod $n$) 이다.

  • ex
    $25^{120}$ mod 143 = $25^{(11-1)(13-1)}$ mod 11 X 13 = 1
    $19^{60}$ mod 77 = $19^{(7-1)(11-1)}$ mod 7 X 11 = 1

• Euler's Theorem 응용
  $a^{\varphi(n)}$ mod n = 1 이니까

  • $a^{\varphi(n)\times k + 1}$ mod n = a
  • $a^{\varphi(n) + 1}$ mod n = a

  • ex
    $25^{1201}$ mod 143 = $25^{120\times 10 + 1}$ mod 11 X 13 = 25
    $19^{481}$ mod 77 = $19^{60\times 8 + 1}$ mod 7 X 11 = 19