Randomness

bad case

• netscape secure socket layer(SSL)
  • predictable 하다

good case (true random number generators)

• radioactive decay
• thermal noise
• polarization of photons
• timing of movements of a hard disk read/write head
  ...

🌻PRNGs : Psuedo Random Number Generators

$X_{n+1} = (aX_n+b)$ mod $m$
-> may look random, but predictable

• automatically create long runs of numbers with good random properties
• but eventually the sequence repeats
• because $X_{n+1}$ and $X_{n}$ is leaner!

⚠️ Linear Complexity should be avoided!__

• $X_{n+1}=f(X_n)$ 의 경우 linear 하다

• 평가방법

  • Berlekamp-Massey Algorithm
    • 이 알고리즘은 minimal polynomial of linearliy recurrent sequence in an arbitary field!
  • Maurer's Universal Test
    • test a sequence or system for strength
    • it should not be possible to significantly compress the output sequence
  • Next bit Test
    • 첫 output의 x bits dms (+1) bit절반 이상이 바뀌어야한다.

🌻 CSPRNG : Cryptographically Secure Pseudo Random Number Generators

based on existing cryptographic primitives

• Secure Block Cipher running a Counter
  • Random Key + Counter (0, 1, 2, 3, ...)
• Secure Hash running a Counter
  • Random Key + Counter
• Stream Cipher running a Counter
  • Pseudorandom stream + Counter
• Shamir's PRNG
  • suggested that RSA could be used as a PRNG, but slow

Cryptographic PRNG

• system use a complexity/number theory approach to PRNG

Standard Examples (practical PRNGs)

• ANSI X9.17
  • Financial Inst. Key Management
• FIPS 186-4 Generator
  • Digital Signature Standard v.4
• NIST SP800-90A
  • Recommendation for Random Number Generator Using Deterministic Random Bit Generators
• ANSI X9.82
  • Dual_EC_DRBG

🦋 Blum-Micali Generator

• has unconditional security prrof

• Based on discrete logarithm problem(NP)

  • $X_{i+1} = g^{X_i}$ mod $p$
    where p is a prime, g is a primitive root modulo p , and $x_0$ is a seed

• output of generator is

  • '1' if $x_i$ is less than (p-1)/2
  • '0' otherwise

• primitive root modulo

  • $g$ is primitive root modulo $n$ if every number a coprime to $n$ is congruent to a power of $g$ modulo $n$
  • ex) 3 is a primitive root modulo 6
    

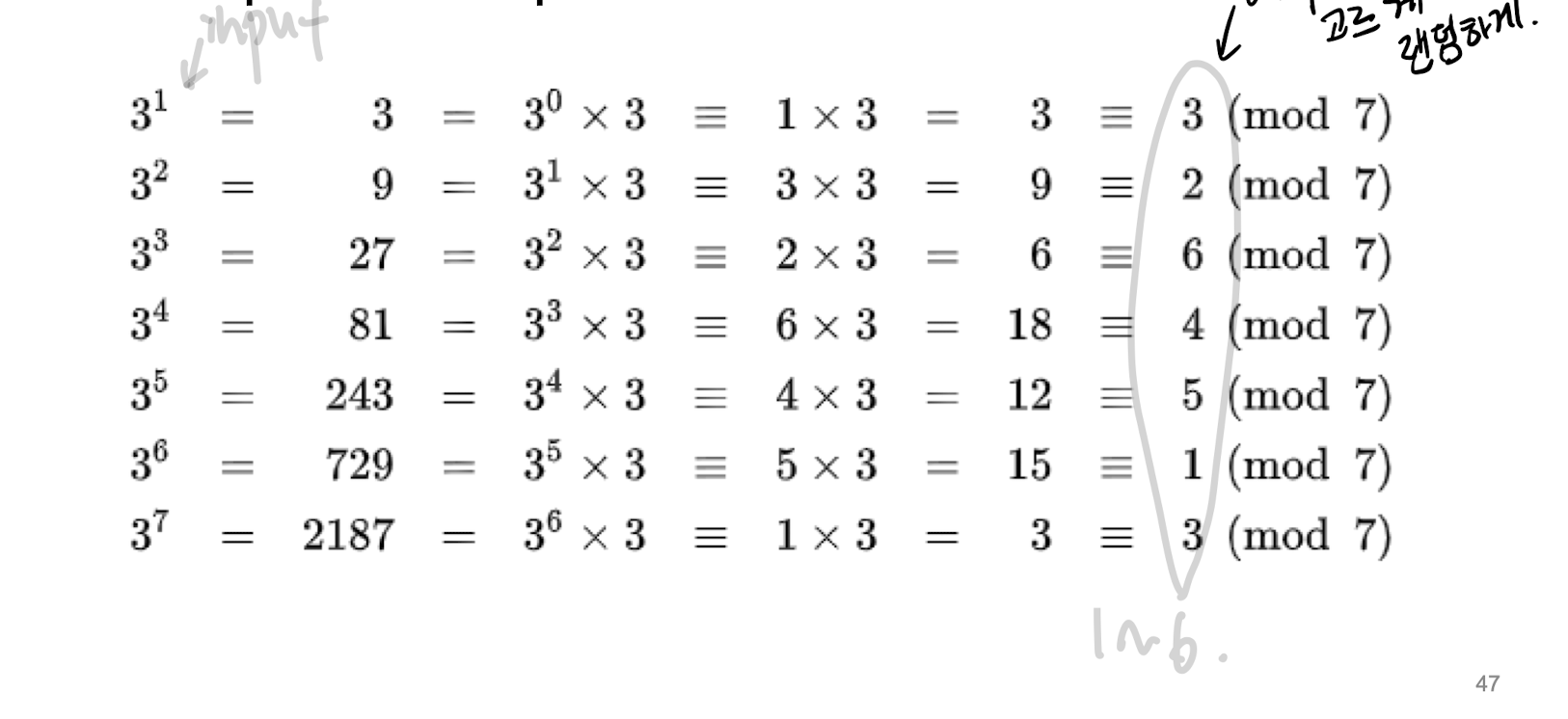
🦋 Blum, Blum and Shub (BBS)

• n = p * q 일때 오른쪽->왼쪽은 어렵고 왼쪽->오른쪽은 쉽다

• based on difficulty of integer facotization

• n = pq이고, seed integer 은 s일때
  $x_i=x^2_{i-1}$ mod $n$
  where $x_0 = s^2$ mod $n$

• can directly calculate $x_i$ via Euler's Theoerem
  $x_i=(x^{2^imod\lambda(n)}_0)$ mod $n$
  where $\lambda(n)=\lambda(pq)=lcm(p-1, q-1)$

• output

  • either the bit parity or the least significant bits of $x_i$

• ex