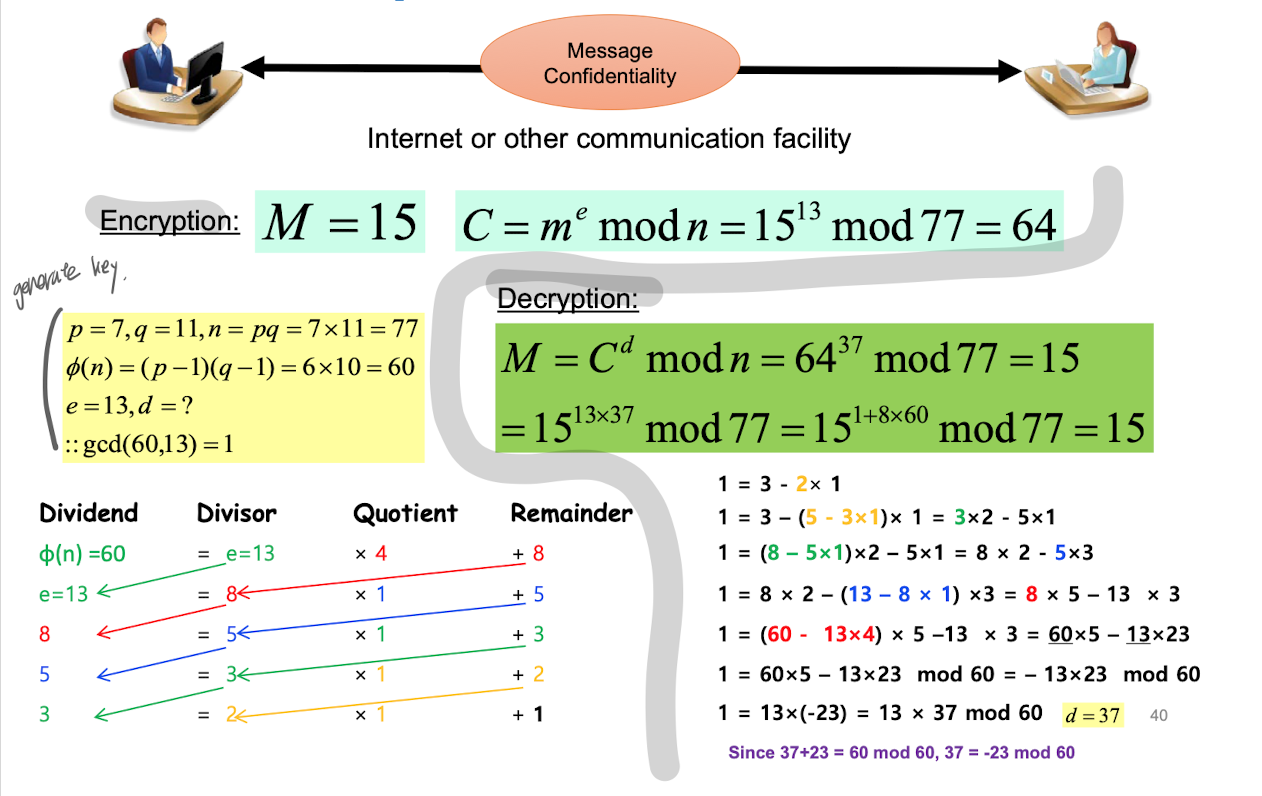
before get in...
🌻 Symmetric Cryptography <-> Asymmetric Cryptography
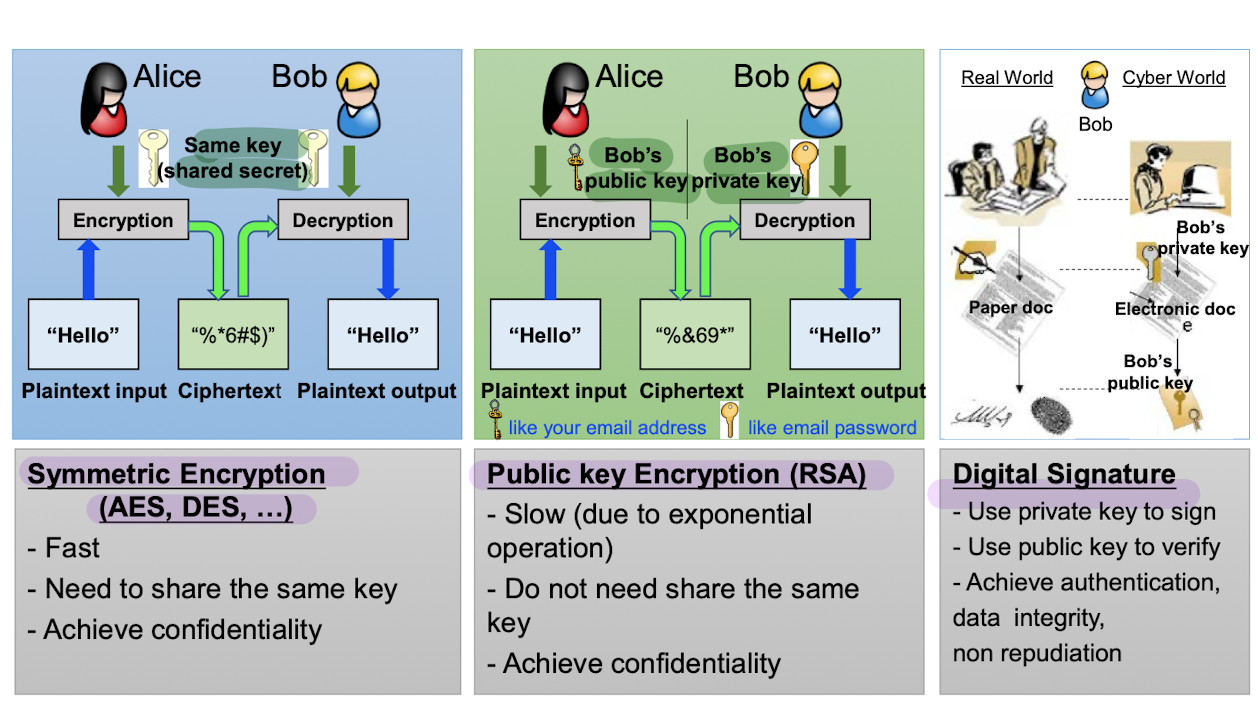
✉️ Symmetric Cryptography
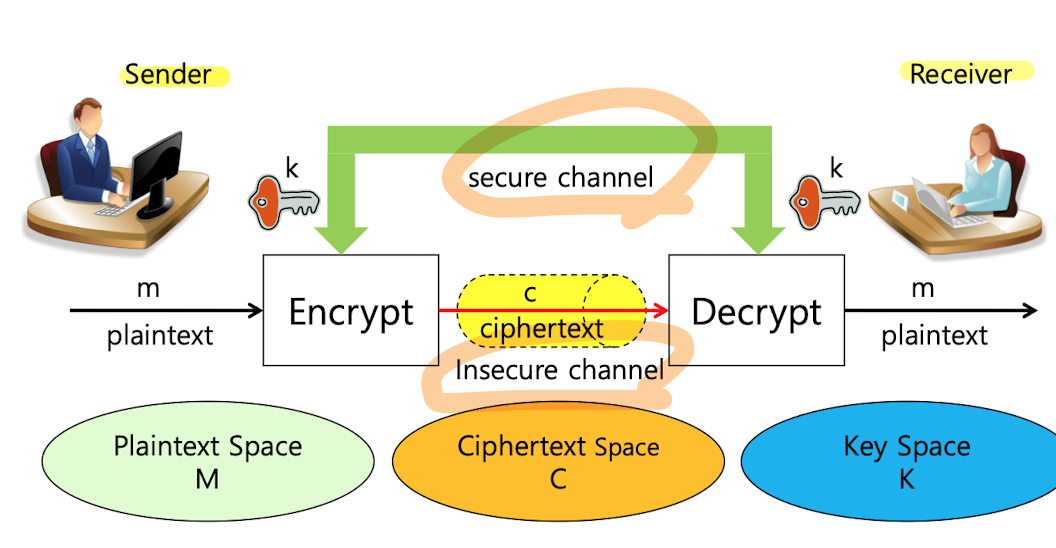
- receiver, sender 모두 같은 key를 가진다
- secure channel로 공통 key를 교환
- insecure channel로 cipertext(C)를 교환
- 용어정리
- C : ciphertext
- M : palintext
- K : key
- 단점
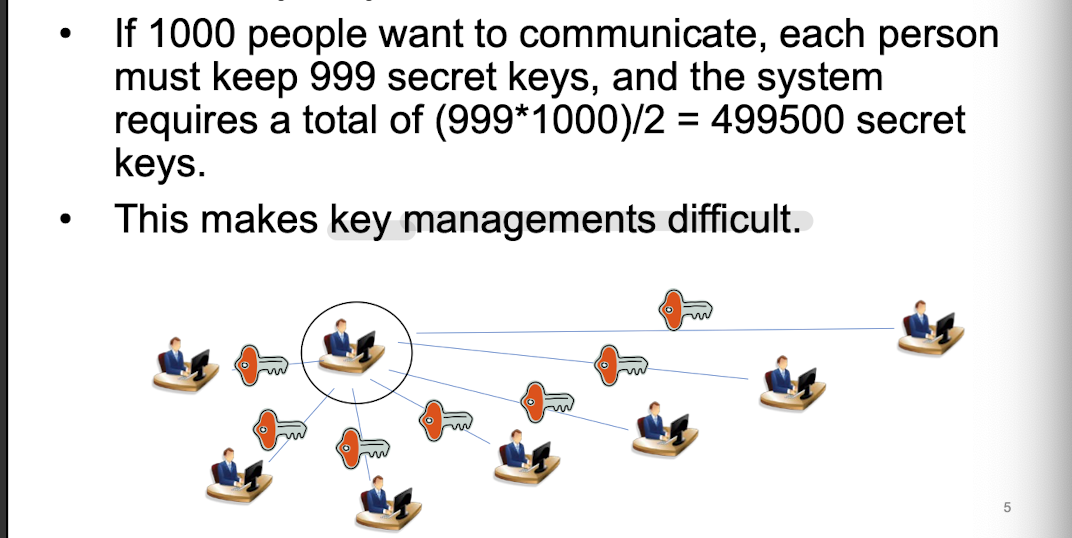
- 사람이 늘어날 수록 1:1로 가지는 공통키 관리가 힘들다
✉️ Asymmetric Cryptography
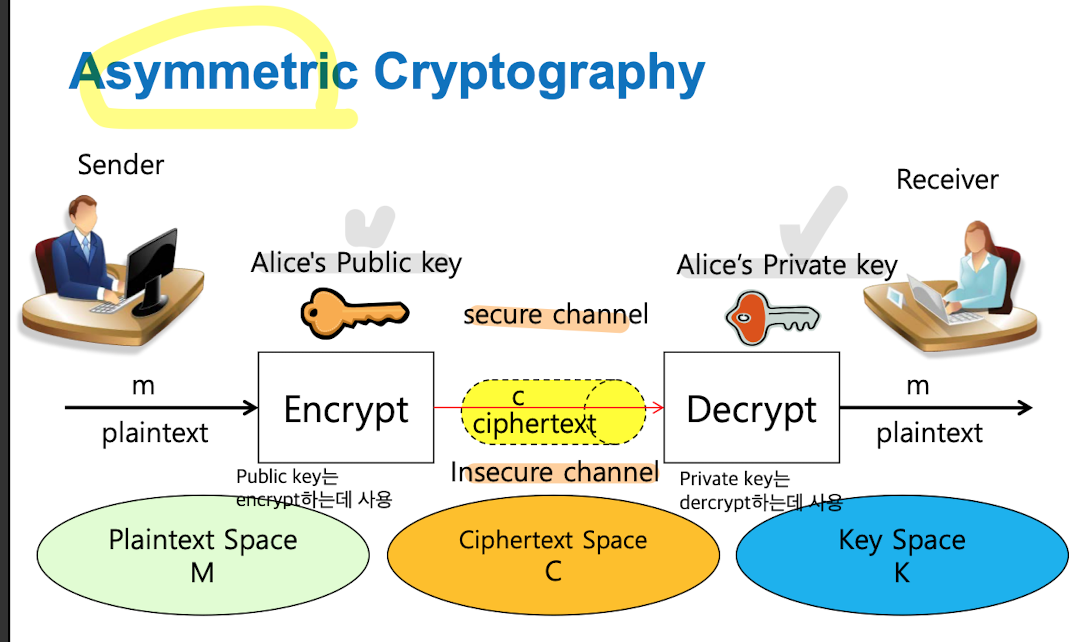
-
sender는 public key, receiver는 private key를 가진다.
-
public key
- encrypt하거나, signatures를 verify하는데 쓰임
- 누구나 알 수 있다
-
private key
- decrypt하거나, sign(=create) signatures 하는데 쓰임
- 오직 recipient만 알고 있음
- 장점
- key관리가 용이
- digital signature 사용 가능
- 특징
- algorithm과 encryption key(public key)만 알아서는, private key를 알아내기 힘들다(=computationally infeasible to find)
- 반면, 키를 두개 다 안다면 en/decrypt 하기 쉽다
- 활용
- encrypt & decrypt
- digital signature
- key exchange (message가 아니라 key 교환)
🌻 Security of Public key algorithm
-
특징
- key space가 충분히 넓어야함
- 512bits, 1024bits...
- 매우 큰 숫자들의 연산이 필요함-> symmetric key schemes에 비해 slow
- known hard problem에 rely함
- key space가 충분히 넓어야함
-
known hard problem : "trapdoor function"
- 들어갈땐 맘대로지만 나갈땐 아니란다 (ex)식충식물)
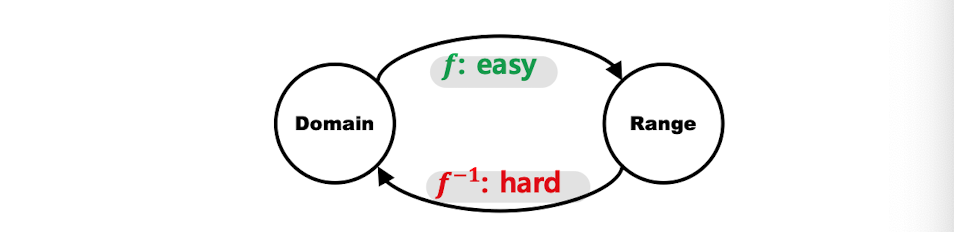
- 예시
- prime factorization
- 두개의 큰 수인 p, q 있을때, pq=z 계산하기 쉽지만, z에서 p와 q를 역으로 뽑아내기는 힘들다
- EX) RSA, Paillier, etc..
- discrete logarithm problem
- 두개의 정수 g와 x가 있을때, 계산하기 쉽지만, x가 주어졌을때 g와 a를 역으로 알기는 어렵다
- Diffie-Hellman, Digital Signature, Elliptic Curve, ElGamal, etc..
- Other
- Naccache-Stern(Knapsack), Algebraic Erase(Matrix Permutation), HFE (Multivariate Quadratic Equation), etc..
- prime factorization
- 예시
- 더 넓게 spread될 수록 more secure하다
🌻 RSA
INTRO
-
RSA의 수학적 배경
-
RSA cryptosystem
-
RSA digital signature
-
RSA cryptanalysis
🦋 RSA의 수학적 배경
-
Fermat's Theorem
where p is prime and gcd(a,p) = 1
also,- primality testing(소수 체크)에 매우 유용하다.
-
Euler's Theorem
for any a, n where gcd(a,n)=1
(소수일때) / (소수 p*q로 이루어졌을때)- example
- a = 3, n=10, 일때,
=1 mod 10
- a = 3, n=10, 일때,
- example
🦋 testing for primality
-
RSA포함 많은 cyptographic algorithm들은 very large prime numbers를 랜덤으로 고르는 경우가 많다.
-
"there are infinitely many primes"
-
n이하의 prime number 몇개나 있을까?
보다 작은 prime num의 갯수- 이하의 소수는 몇개 있을까? -> -> 3838
- 시간복잡도
- naive하게 모든경우 시도할땐 O(n)
- n에게 n/2보다 큰 prime num이 존재하지 않는단걸 알았을때의 시간복잡도는
-
주어진 p가 prime인지 판단하는법
이 성립하면 p는 소수, 성립하지 않으면 소수가 아님
a는 p보다 작은 random num을 많이 골라서, 테스트해본다.- 공식성립 = probabily prime
- 공식성립 X = not prime
-
예시)
n=221은 소수인가?
1<a<221 사이에서 a를 ranomly pick.
a = 38일때,
221은 prime num일수도 있다
a = 26일때,
221은 prime이 아니다 -
Miller-Rabin algorithm
odd integer n>2가 있을때,
n-1 은 로 표현될 수 있다.
단, k>0이며 q는 odd 이다.prime num과 공식 합칠 시 prime num test
n이 prime num인지 확인하려면 , 두가지 확인해야- 조건1) 1 mod n
- 조건2) =-1 mod n = n-1 mod n
(단, q는 홀수, k>0이다.) - 조건1O OR 조건2O = probably prime
- 조건1X OR 조건2X = not a prime
-
도출과정
mod n
-> mod n
-> = 0 mod n -
miller labin algorithm 활용한 소수 검사 코드
# repeat for primality testing! MILLER-RABIN(n): 1. Find integers k>0, q odd, so that n-1 = (2^k)q 2. Select a random integer a, 1 < a < n-1 3. if a^q mod n = 1, then return 'probably prime' 4. for j = 0 to k-1 do if a^{{2^j}q}mod n = n-1, then return 'probabily prime 5. return 'composite' // not prime -
예시

Integer Fctorization Problem
- input and output
- input : N
- N은 odd composite integer 이며,
- N은 pq와 같이 at least two distinct prime factors로 이루어져있다.
- output
- primes p and q
- input : N
- large N is difficult!
- p,q가 주어지면 N=pq를 계산하는건 쉽다.
- N이 주어지고, p,q를 계산해내는것은
- N이 작을땐 쉽고
- N이 클땐 매우 어렵다
🦋 RSA 동작 과정
-
😊 generating RSA keys
public key : (n, e)
private key : (n, d)- p and q are large primes!
- n = pq
- 💬 1 < e < 이고,
gcd(e,)=1 인 정수 e는
public key 에 사용! - 💬 1 < d < 이고,
ed=1(mod ) 인 정수 d는
private key 에 사용!- d는 modulo 에서 e의 inverse이다.
- extended Euclidean algorithm으로 계산 가능
-
Encryption : mod
Decryption : mod
(m = plaintext, c = ciphertext)
-
example
🦋 RSA 주의사항
- currently..
- 1024bit-RSA(309 digits) 가 주로 쓰인다.
- |p-q| 는 가급적 커야한다.
- n=pq는 중복되어서는 안된다.
- common modulus attack 가능하기 때문

- common modulus attack 가능하기 때문
- 과 n을 알면 attacker가 unknwon p를 풀수 있다.
🌻 Implemented RSA
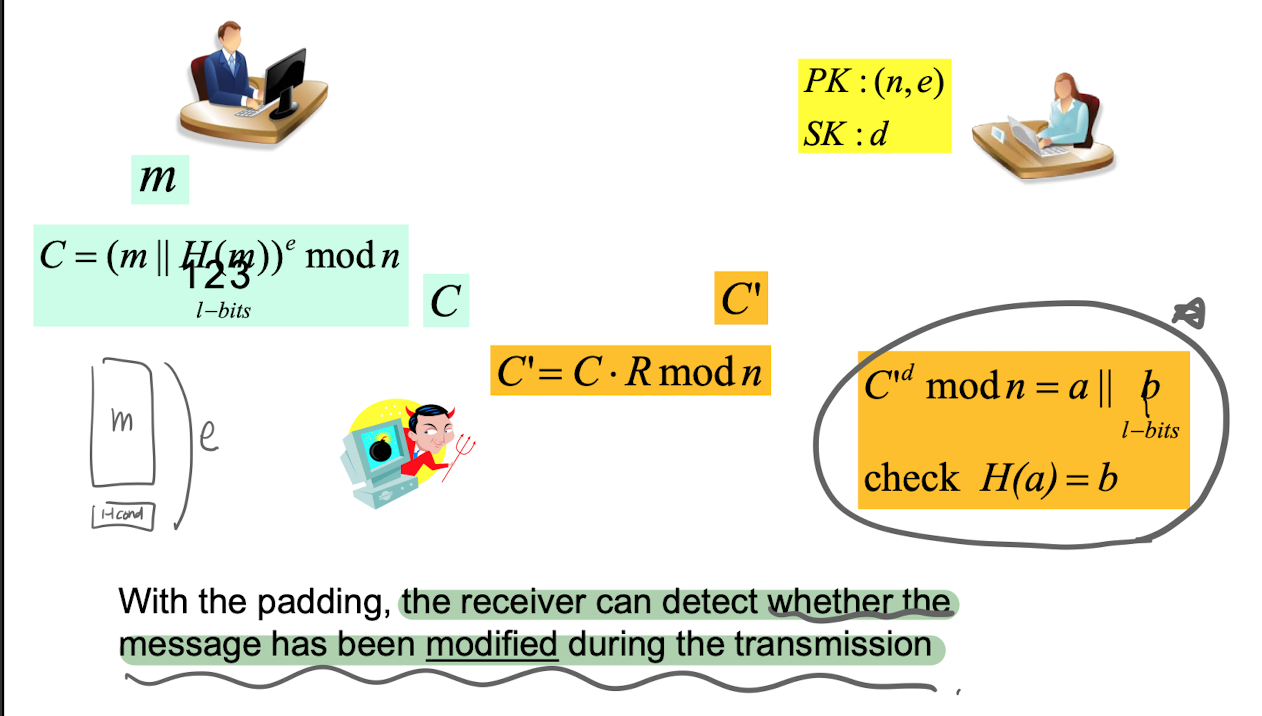
✉️ hasing is required in RSA!
- with a hash padding,
the receiver can detect wether the message has been modified during transmission
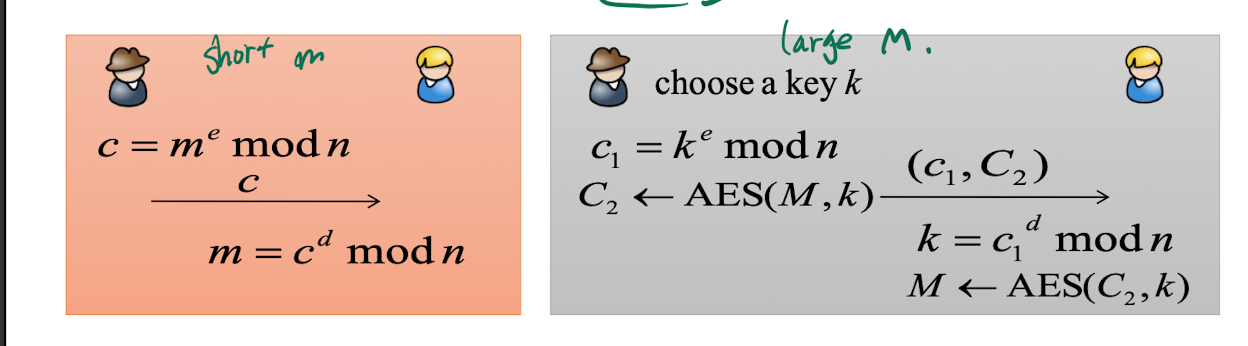
✉️ How to encrypt a long message! -> AES와 섞어쓰자!
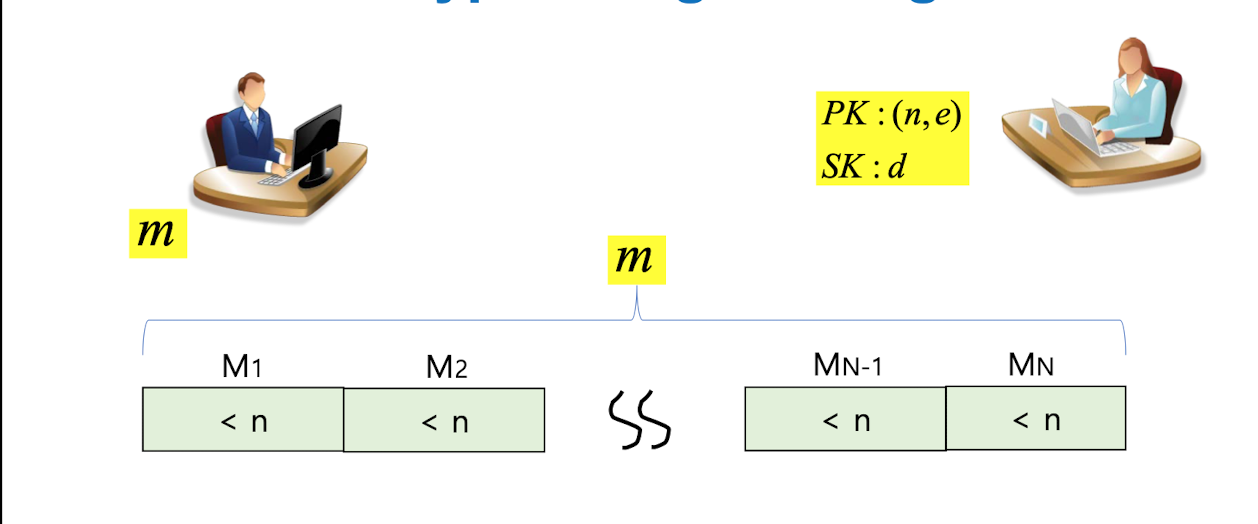
-
위의 그림처럼 m(메세지)이 n보다 작은 들로 쪼개졌을때 efficiency problem 발생
-
symmetric 과의 비교
|encryption algorithm|speed|shared secret key|
|---|---|---|
|symmetric ex)AES|FAST|YES (need sharing a secret key in advance)|
|RSA|SLOW(100~1000배정도 느려서, 짧은 크기의 message encryption에 주로 쓰임)|NO (only need receiver's public key)| -
길이에 따라 AES와 섞어쓰자 !
🦋 digital signature
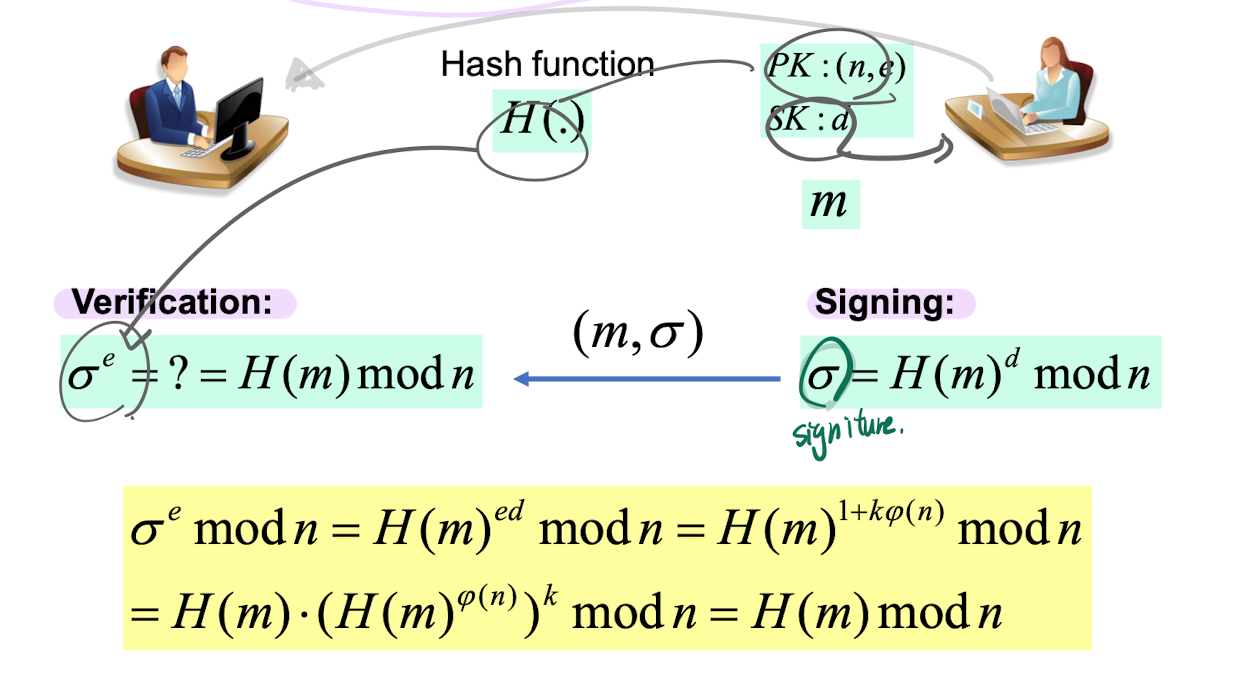
message sender는 message(m)와 함께 signature()를 보낸다!
receiver는 이를 verify 할 수 있다!
- 장점
- reduce size : long message m의 경우, hash(m)=h(m)의 길이는 훨씬 짧다
- improve security : attacker 중간 조작 가능성 차단
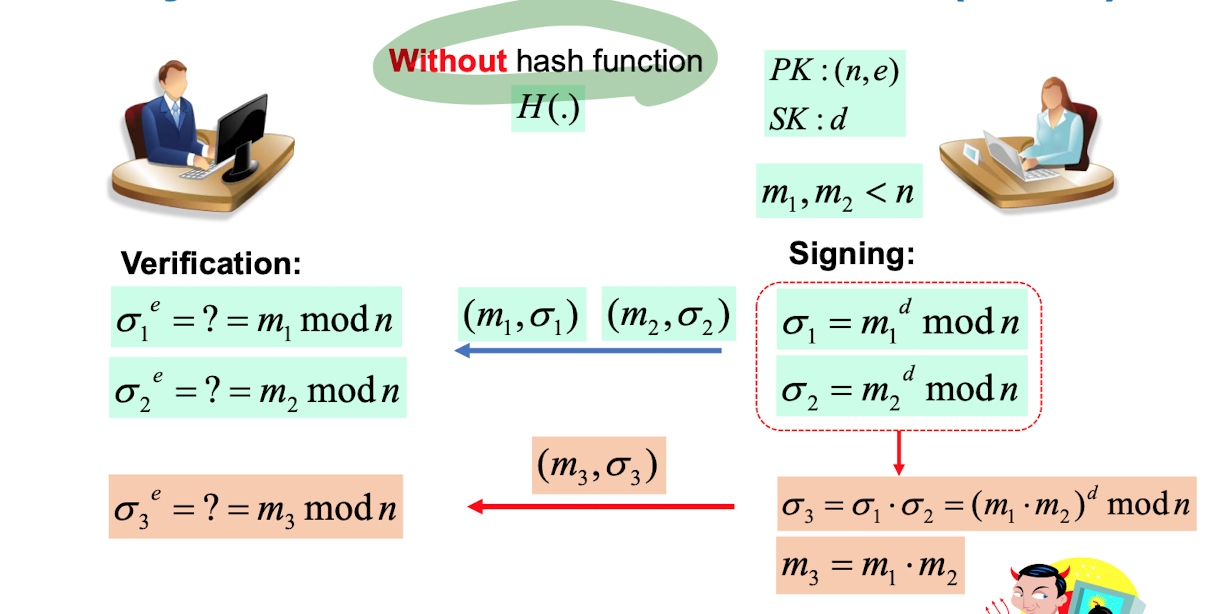
(은 조작된 메세지이다. )
안전하고 + 긴 메세지 보내기
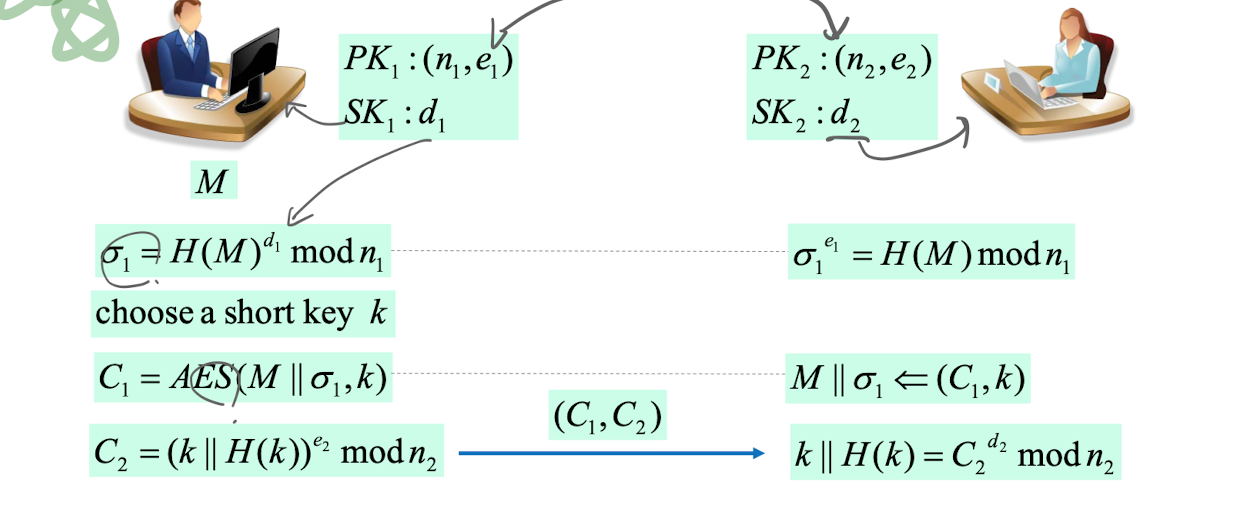
- 효과
- privacy (confidentiality)
- data authentication (data intergrity)
- non-repudiation
- user authentication