Dynamic Programming - 개념

Yona·2022년 1월 6일

🌻 algorithm

목록 보기

12/18

피보나치 수열 : 단순 점화식의 구현 -> DP의 필요성

점화식 : $a_{n+2}=f(a_{n+1}, a_n) = a_{n+1}+a_n$
실제 구하는 과정
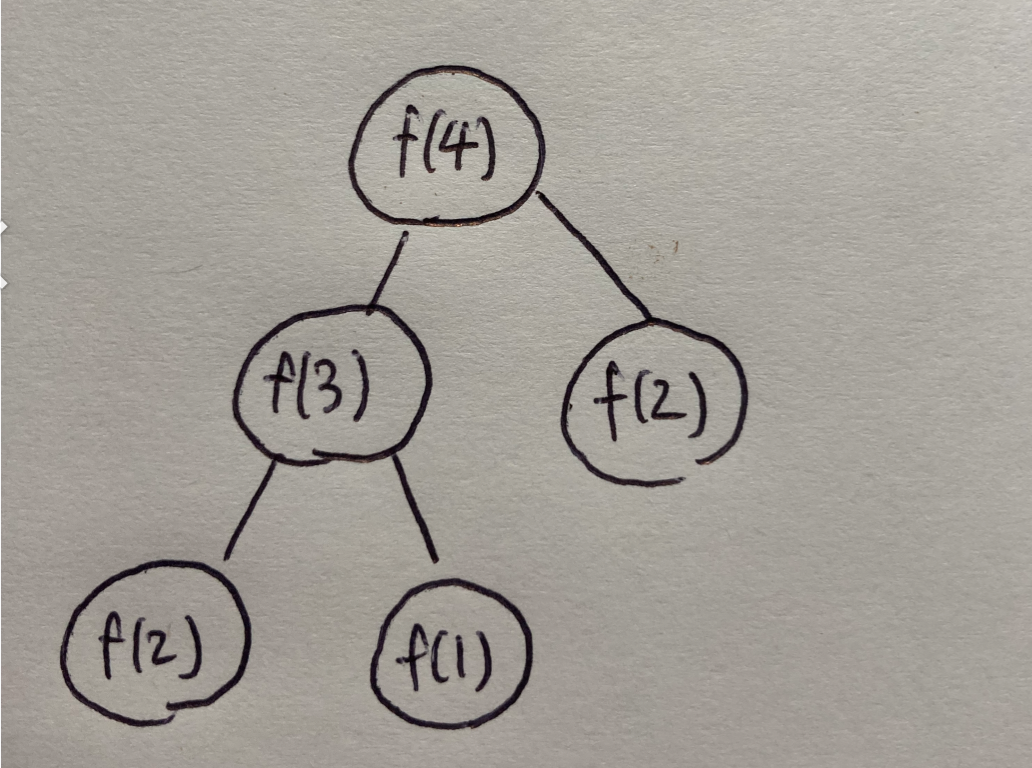
코드

def fibo(x) :
  if (x == 1 or x == 2) :
    return 1
   return fibo(x-1) + fibo(x-2)

printf(fibo(4))

이때의 시간 복잡도 : $O(2^N)$
동일한 함수가 반복적으로 호출되기 때문이다!
- 예시 ) fibo(6) 호출시
  -> 낭비. 비효율적.
  재귀함수를 사용해서 만드는게 끝이 아니라, 더 효율적으로 계산하고싶다. -> DP

Memoization

Memoization
DP를 구현하는 방법 중 한 종류로,
한 번 구한 결과를 메모리 공간에 저장해두고, 같은 식을 다시 호출하면
메모한 결과를 그대로 가져오는 기법.
= 메모이제이션 = 캐싱 Caching

예시) 피보나치 + 메모이제이션

# 한 번 계산된 결과를 Memoization하기 위한 리스트 초기화
d = [0]*100

# 재귀함수로 피보나치 구현 (top-down형식)
def fibo(x) :
  # 종료조건 = 1이거나 2일때 
  if x == 1 or x == 2 :
    return 1
  # 이미 계산한 적 있는 문제라면 그대로 반환
  if d[x] != 0 :
    return d[x]
  # 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
  d[x] = fibo(x-1) + fibo(x-2)
  return d[x]

print(fibo(99))

시간복잡도

이때의 시간복잡도는 O(N)
- f(1) 구한다음, 그 값이 f(2)에 사용되고
  f(2)가 f(3)을 푸는데 사용되는 방식으로 이어지기 때문.
===============시간복잡도 더 검색해서 보충하기==============

DP 조건

dynamic programming 사용 조건
1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.

분할정복과의 차이점

공통점 : 큰 문제를 작은 문제로 나눔
차이점 :

divide and conquer	dynamic programming
한번 pivot 원소가 자리를 변경해서 자리 잡게 되면, 그 기준 원소의 위치는 더이상 바뀌지 않고 그 피벗값을 다시 처리하는 부분 문제는 존재하지 않는다.	한번 해결했던 문제를 다시해결한다. 이미 해결된 부분 문제에 대한 답을 저장해 놓고, 이 문제는 이미 해결이 됐던 것이니 다시 풀 필요가 없다고 반환한다.

재귀보단 반복문!

재귀 함수 사용시, 컴퓨터 시스템에는 함수를 다시 호출했을때
메모리 상에 적재되는 일련의 과정을 따라야해서 오버헤드가 발생할 수도
때문에 일반적으로 재귀보다 반복문이 DP에서 성능이 좋다.
재귀함수의 스택 크기가 한정되어있을 수도 있다.
(sys라이브러리의 setrecursionlimit()을 이용해 재귀 제한 완화 가능하긴 함)