Dynamic Programming - 예제

Yona·2022년 1월 6일

DP 알고리즘 이코테

🌻 algorithm

목록 보기

13/18

1로 만들기

이코테 책 217p

문제

시간제한
- 1초
입력
- 정수 X (1<=X<=30,000)
출력
- 연산을 하는 횟수의 최솟값
문제 요약
- 주어지는 정수 X에게 사용 가능한 연산은 4가지
  - X가 5로 나누어떨어지면, 5로 나눔
  - X가 3로 나누어떨어지면, 3로 나눔
  - X가 2로 나누어떨어지면, 2로 나눔
  - X에서 1을 뺌
- X가 주어지면 연산 4개를 적절히 사용해서 1만드려고 함. 연산 사용하는 횟수의 최솟값 출력하시오.

풀이

1. 완전탐색 경우를 있는그대로 그려보자

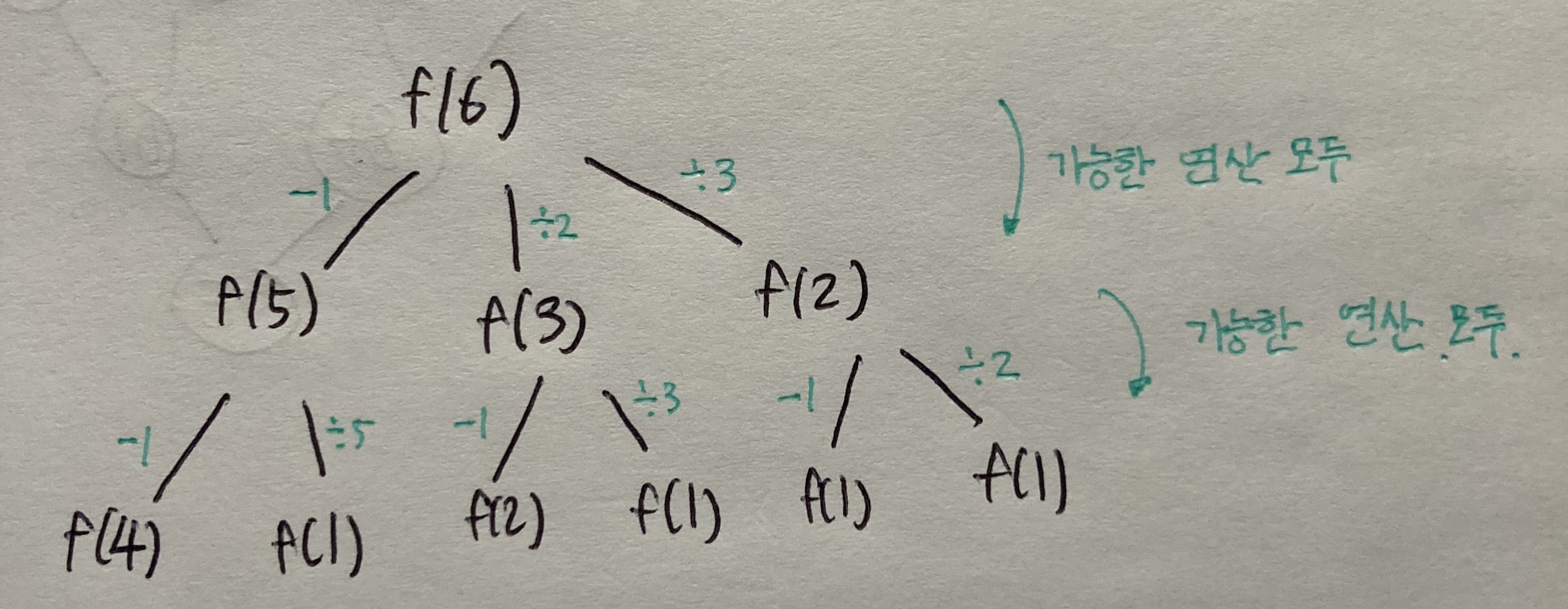
2. DP 가능 여부 판단

같은 함수들이 동일하게 여러번 호출된다.
동일한 함수에서 구하는 값들은 동일해야한다.

3. 요구 내용을 점화식으로 표현

$a_i = min(a_{i-1},a_{i/2},a_{i/3},a_{i/5})+1$

⚠️ 식 자체를 받아들이려고 하지 말고 (my Dagari로 될리가없다)
그래프 이미지를 보면서 생각하자! !
그냥 저 그래프를 식으로 옮긴 것 뿐이다.

4. 코드로 구현

# 정수 X 입력받기
x = int(input())

# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 30001

# DP 진행 (bottom-up)
for i in range(2, x+1) :
  #현재의 수에서 1을 빼는 경우
  d[i] = d[i-1] + 1
  # 2로 나누는 연산이 가능한 경우
  if i % 2 == 0 :
    d[i] = min(d[i], d[i//2] + 1) 
  # 3으로 나누는 연산이 가능한 경우
  if i % 3 == 0 :
    d[i] = min(d[i], d[i//3]+1)
  # 5로 나누는 연산이 가능한 경우
  if i % 5 == 0 :
    d[i] = min(d[i], d[i//5] + 1)

1번의 무조건 계산과 3번의 if문에서 계속
인덱스 i에 해당하는 최소의 연산횟수를 저장해둔 d[i]와 비교하면서,
인덱스 i의 새로운 최소의 연산횟수가 등장하면 갱신한다.
이런 식으로 $a_i = min(a_{i-1},a_{i/2},a_{i/3},a_{i/5})+1$ 를 수행하고 있다.