[2020 International Journal of Forecasting] DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks

Abstract

• Probabilistic forecasting: 주어진 과거 데이터를 기반으로 미래 시계열 값의 확률 분포 예측
• 본 논문의 모델은 auto-regressive recurrent network model을 사용하여 정확도 높은 Probabilistic forecasting 방법론을 제안

1. Introduction

이전 예측 모델들 (calassical Box-Jenkins methodology, exponential smoothing techniques, state space models)은 과거의 관측들로부터 독립적으로 추정됨.

하지만, 다음과 같은 문제점들이 있다
1. 시계열의 길이가 서로 다름
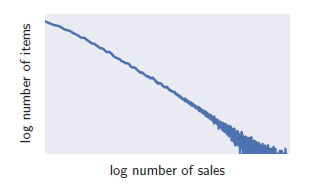
2. 크기 분포가 심하게 치우쳐져 있음

• 분포의 scale-free특성은 속도에 따라 시계열을 하위 그룹으로 나누는 것을 어렵게 함
• 그룹 기반 정규화 체계는 각 그룹내에서 속도가 크게 다르기 때문에 실패할 수 있음
• 왜곡된 분포는 입력 표준화 또는 배치 정규화와 같은 일반적으로 사용되는 특정 정규화 기술의 사용을 덜 효과적으로 만듦

따라서 본 논문에서는 autoregressive recurrent networks기반으로 만든 예측모델 DeepAR을 제안함

[Contribution]

(1) 시계열의 크기가 변화하는 경우에 대한 특별한 처리 뿐만 아니라 negative Binomial likelihood를 통합하는 확률적 예측을 위한 RNN Architecture
(2) 이 모델이 다양한 입력 특성에 걸쳐 정확한 확률적 예측을 생성한다는 것을 경험적으로 입증

[Key Advantages]

(1), (2)는 전통적 기법과의 차별점 & (3), (4)는 global method화 하는 것

(1) 주어진 공변량에 대한 계절적 행동과 의존성을 학습함에 따라 복잡하고 그룹 의존적인 요소를 포착하기 위해 최소한의 수동 기능 엔지니어링이 필요함
(2) DeepAR은 모든 하위 범위에 대한 일관된 정량적 추정치를 계산하는데 사용할 수 있는 몬테카를로 샘플의 형태로 확률적 예측을 시행함
(3) 유사한 item에서 학습을 하기 때문에 과거가 없는 item도 예측 가능함
(4) Gaussian noise를 가정하지 않지만, 데이터 통계적 특성에 맞는 다양한 범위의 우도함수를 사용할 수 있음.

=> 이러한 확률적 예측은 위험을 최소화하고 불확실성 아래 최적의 decision을 만듦.

2. Related Work

3. Model

1. 과거 데이터 z와 공변량 x가 주어졌을 때, 미래 데이터 z가 나올 조건부 확률을 모델링하는게 목표!
   
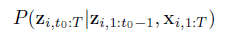
2. 모델 분포가 likelihood의 곱으로 이루어짐
   
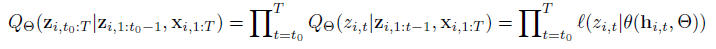
3. Autoregressive recurrent network의 결과 h에 의해 parameterized됨.
   
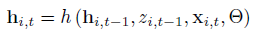
4. 모수 theta가 주어지면, joint samples를 얻을 수 있음.
   

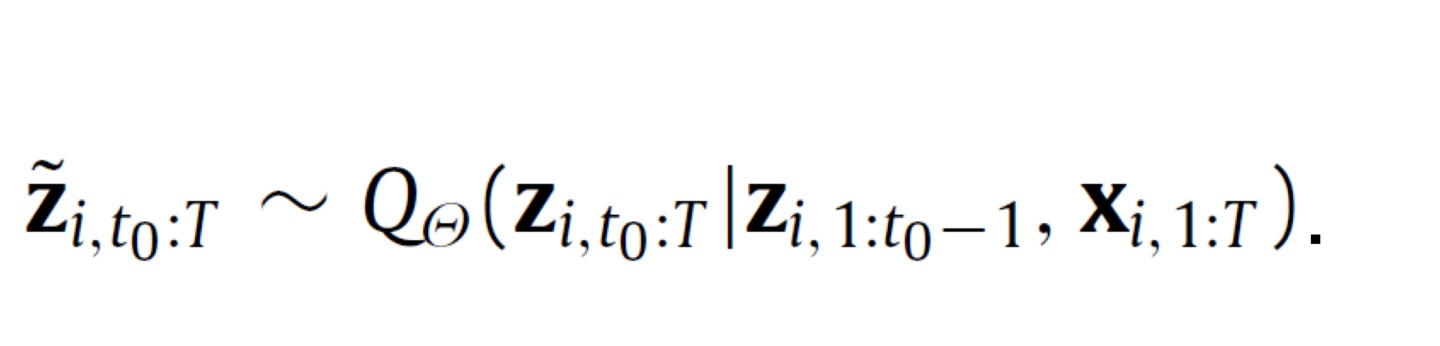
3.1. Likelihood model

• Likelihood는 "noise model"을 결정함
• 본 논문 실험에서는 2종류의 likelihood를 사용함

1. Gaussian likelihood for real-valued data
   • 평균과 표준편차 사용
   • 평균은 output의 affine function으로 나옴
   • 표준편차는 softplus activation에 의한 affine transformation을 적용해 얻어짐
     
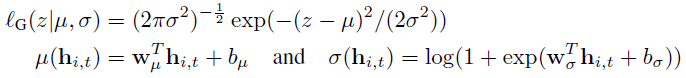
2. Negative-binomial likelihood for positive count data
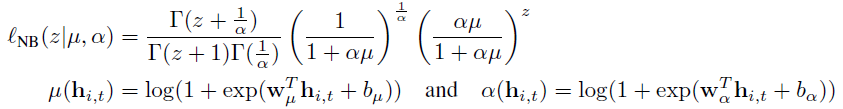
   • 평균과 shape parameter 사용
     

3.2. Training

위의 log-likelihood 함수를 최대화하는 방향으로 학습 진행

3.3. Scale handling

1. Autoregressive model이기 때문에 input과 output의 크기를 맞춰야 함
   -> input을 input layer에서의 적절한 번위에서 scale하도록 학습하고 ouput에서 이 scaling을 적용한다.
   
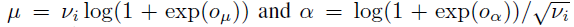
2. Data imbalancing 때문에 학습 요소를 uniform하게 랜덤으로 뽑는 optimization 절차는 underfitting을 초래한다.
   -> non-uniformly하게 샘플링해서 학습함

3.4. Features

• 본 논문에서 사용한 covariates
  - "age" feature: the distance to the first observation in that time series
  • day-of-the-week and hour-of-the-day for hourly data, week-of-year for weekly data and month-of-year for monthly data
  • a single categorical item feature
• 모든 covariates를 zero mean and unit variance로 표준화함

4. Applications and Experiments

• Figure 4는 불확실성 증가에 대한 그림으로 DeepAR이 불확실성을 더 잘 포착하는 것을 알 수 있음
• Figure5는 기간의 길이에 다른 수렴속도로, 정확히 예측할수록 Converage(p)=p에 더 가까움

5. Conclusion

• 연관된 시계열 데이터로부터 global model 학습 가능
• rescaling과 속도기반 샘플링으로 다양한 크기의 데이터 다룰 수 있음
• 높은 정확도로 교정된 확률 예측을 할 수 있음
• seasonality와 uncertainty growth와 같은 복잡한 패턴 학습 가능