[2020 preprint] Multivariate Probabilistic Time Series Forecasting via Conditioned Normalizing Flows

Abstract

다변량 시계열 예측에서는 변수간의 독립성을 가정함. 하지만 변수간의 통계적 의존성을 모델링하는 것은 정확도를 향상시킴.

그러나 다변량 모델에서 종종 단순한 parametric 분포를 가정하고 고차원을 다루지 않음.

따라서 본 논문에서는 Conditioned Normalizing Flow를 이용한 Autoregressive Deep Learning로 다변량에서의 시계열 역학을 다루고자 함.

이 모델은 future에서의 extrapolation에서 좋은 성능을 보였으며, 고차원 분포로서 flow의 유연성을 가지며, 컴퓨팅적으로 tractable하다는 점이 있음

1. Introduction

• 시계열 예측의 불확실성 모델링 문제는 이상탐지 또는 의사결정과 같은 downstream task에 대한 결과를 얼마나 신뢰해야 하는지를 평가하는데 매우 중요함.
• 또한 다변량 모델은 단변량 모델에서 다루지 못하는 것을 다룰 수 있음. 예를 들어 과거의 판매량과 다른 시장의 판매량을 함께 사용하거나 특정 도로의 차량 복잡도와 근처 도로의 차량 복잡도를 함께 사용하면 훨씬 정확도가 향상됨.

본 연구에서는 , Masked Autoregressive또는 Real NVP와 같은 Normalizing Flow를 사용하여
다변량 시계열과 시간 역학을 명시적으로 모델링하는 probabilistic forecasting을 위한
end-to-end 훈련가능한 Autoregressive Deep Learning Architectures 제안함
-> 이 방법론은 Normalizing Flow를 사용하기 때문에 광범위한 기본 데이터 분포에 적응하며,
Transformer 기반 모델은 훈련 중에 attention layer의 특징 때문에 매우 효과적임.

2. Background

2.1. Density Estimation via Normalizing Flows

: Normalizing flows는 mapping을 통해 input space의 분포를 단순한 분포로 변형시키는 것임

• The bijection for the Real NVP
  

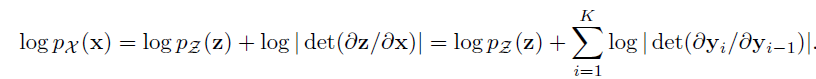
• The Jacobian for the Real NVP
  

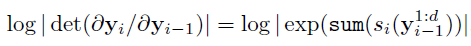
2.2. Self-Attention

여기서 mask M은 right-ward attention(미래 정보)을 필터링하는데 사용됨

3. Related Work

4. Temporal Conditioned Normalizing Flows

• 변수들간의 의존성 파악을 위해 각 timestep마다 full-joint distribution을 사용해야 함
• (-) 그러나 full-joint distribution은 O(D^2)의 시간 복잡도 가짐

" 우리는 상호 작용 시계열 Xt가 확장 가능하며 고차 모멘트를 표현할 수 있는 유연한 분포 모델을 사용하기를 원한다! "

RNN Conditioned Real NVP model

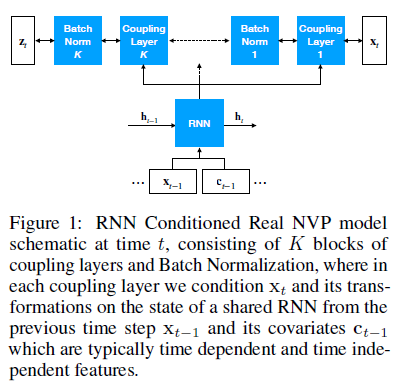
• 모든 flow와 함께 time step에 대해 conditional joint distribution을 모델링함
  (condition은 RNN의 은닉층 또는 attention module에서 t-1시점까지의 시계열 임베딩 값)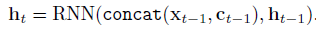
• Stack K layers of a conditional flow module(Real NVP or MAF) and together with the RNN
  

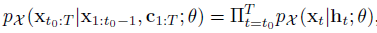
Transformer Conditioned Real NVP model

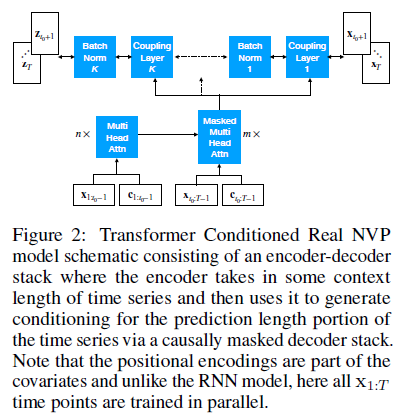
• 'encoder': embeds past x values
• 'decoder': ouputs the conditioning for the flow over future x values via a masked attention module
• 미래 정보 사용 방지와 causal direction 반영을 위해 Mask 사용
• Transformer는 시간 거리 상관없이 모든 과거 데이터에 접근하기 때문에, 더 나은 Normalizing flow를 위한 Conditioning을 생성

4.1. Training

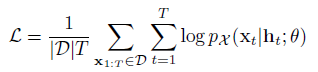
위의 log-likelihood를 최대화하는 방향으로 학습 via SGD using Adam

• Transformer의 computational complexity: O(T^2D)
• RNN의 computational complexity: O(TD^2)
• T: time series length / D: num of variables

4.2. Convariates

• time-dependent / time-independent / lag features

4.3. Inference

• warm-up tiem series past data and covariates

5. Experiments

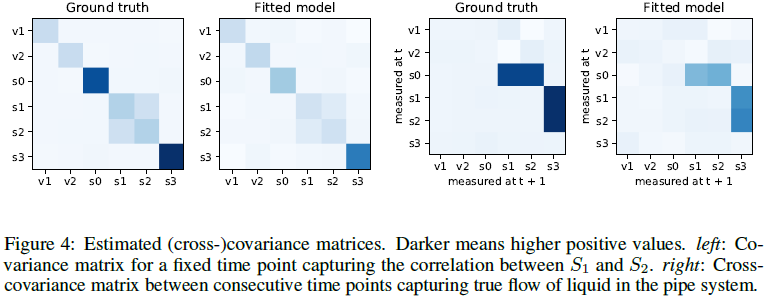
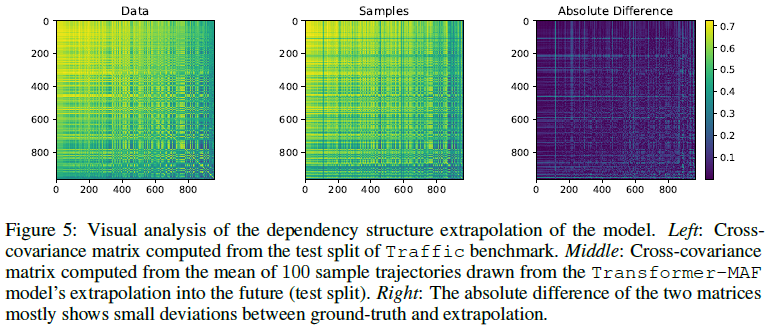
6. Conclusion

• RNN과 Attention과 같은 autoregressive model과 conditional normalizing flows를 결합해 고차원 확률 다변량 시계열 데이터 모델링
• Flow model은 단순한 고정 분포를 가정하지는 않지만, 고차원 데이터 분포를 다룰 수 있음
• 컴퓨팅 효율이 좋고 D가 클 때도 robust함