Time-Series Representation Learning via Temporal and Contextual Contrasting

1. Introduction

• 시계열 데이터에 라벨을 매기는 것은 이미지보다 어려움
• 하지만 딥러닝은 많은 양의 라벨 데이터를 필요로 함
• 따라서 Self-Supervised learning이 라벨없는 데이터의 표현을 효과적으로 추출하는데 큰 기여를 함.
• 그러나 이전 연구들은 이미지에 초점이 맞춰져 있고 이는 시계열에 적용하기 힘듦
  1. Image-based method는 시계열 데이터의 temporal dependencies를 다루지 못함
  2. Image-based method에서 사용되는 augmentation은 시계열 데이터에 적용할 수 없음
• 기존에 제안된 time series-based contrasting method는 특정 데이터에 맞게 제안되어 다른 시계열 데이터에는 사용하지 못하는 한계점이 있음
• 따라서 본 논문에서는 robust & discriminative time series representation을 학습할 수 있는 TS-TCC를 제안함

2. Related Works

2.1. Self-supervised Learning

2.2. Self-supervised Learning for Time-Series

3. Method

[Contribution]

• TS-TCC는 모델의 generalization을 위해 모든 시계열 데이터에 적용 가능한 간단하고 효과적인 augmentation 기반의 contrastive learning을 활용함
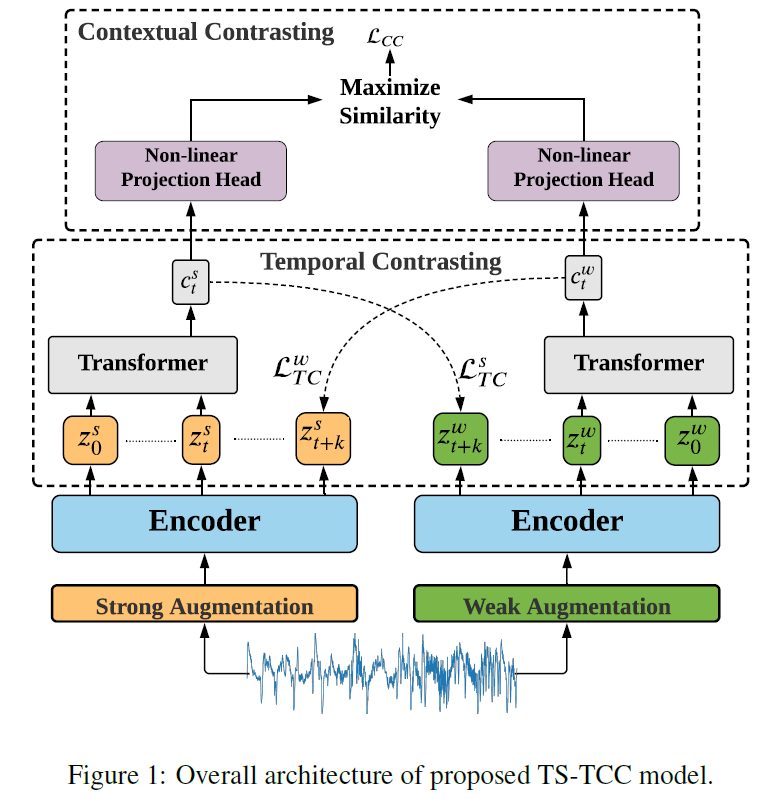
• TS-TCC는 time series data에 weak/strong augmentation을 적용한 결과를 활용하여 representation을 학습할 수 있는 아래 두 모듈을 제안함
  * Temporal contrasting module: weak/strong augmentation에 대해 cross-view prediction task를 통해 모델이 robust representation을 학습하도록 함.
  * Contextual contrasting module: weak/strong augmentation의 context vector에 대한 contrastive loss를 통해 모델이 discriminative time series representation 을 학습하도록 함

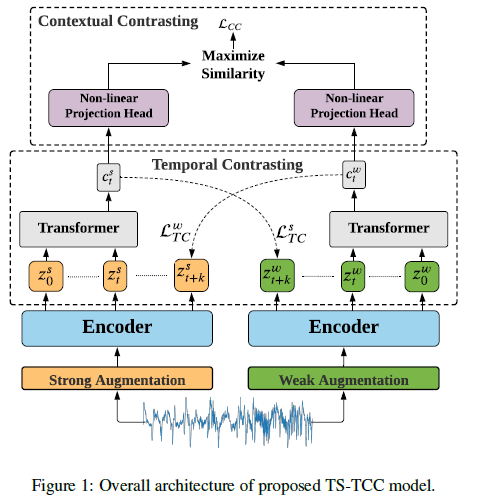
3.1. Time-Series Data Augmentation

• 기존 contrastive learning method는 같은 augmentation으로 2개의 variants를 만들어냄
• 그러나 본 논문에서는 learned representation의 robustness를 향상시키기 위해 서로 다른 augmentation을 사용함.
  * Strong augmentation: permutation-and-jitter strategy 사용 (splitting+random)
  * Weak augmentation: jitter-and-scale strategy 사용 (random+scaleup)
  

3.2. Temporal Contrasting

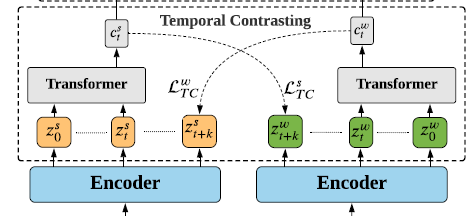
• latent representations z가 autoregressive model인 Transformer를 거치고 ct라는 context vector로 요약함.

• strong augmentation에서 출발한 ct는 weak augmentation에서 출발한 z의 t+1시점부터 t+k시점까지를 예측하기 위해 사용됨.

• 마찬가지로 weak augmentation에서 출발한 ct는 strong augmentation에서 출발한 z의 t+1시점부터 t+k시점까지를 예측하기 위해 사용됨
  

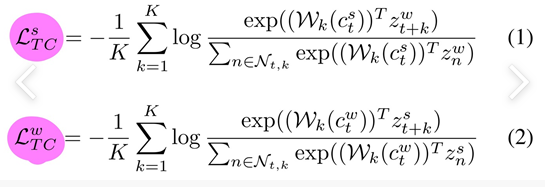
• 위 식들을 기반으로 예측된 representation(ct)과 실제 sample(z_t+1 ~ z_t+k)과의 dot product를 최소화하는 반면, minibatch안의 다른 샘플들 N_t,k의 dot product를 최대화하는 방향으로 학습

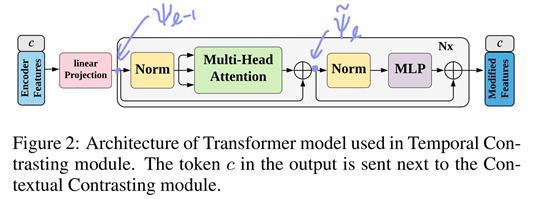
• 위 그림에서 MLP block은 2개의 fully-connected layer와 non-linearity ReLU함수와 dropout으로 구성됨
• Transformer를 사용함으로써 효율성과 속도를 향상시킴
• Pre-norm residual connection을 사용함으로써 더 안정적인 gradient를 생산함.
  

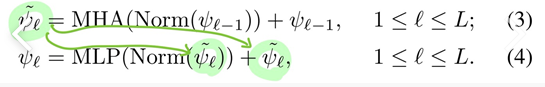
3.3. Contextual Contrasting

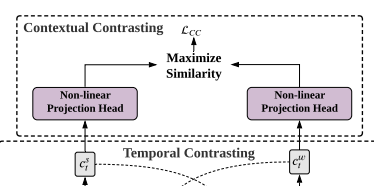
• discriminative representation을 위해서 context vector c_t에 non-linear transformation을 적용함

[최종 Loss 식]

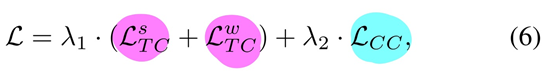
4. Experimental Setup

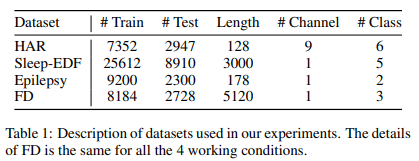
4.1. Datasets

human activity recognition, sleep stage classification and epileptic seizure prediction
&
fault diagnosis dataset (transferability 평가를 위해)

4.2. Implementation Details

(논문 참고)

5. Results

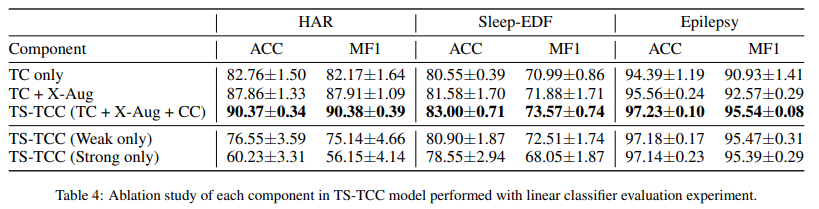
5.1. Comparison with Baseline Approaches

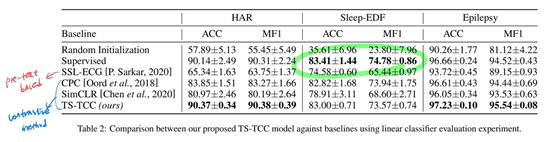
(1) Random Initialization: 랜덤으로 초기화된 encoder위에 선형 분류기 학습
(2) Supervised: encoder와 classifier model 모두에서 지도 학습

• Contrastive methods(CPC, SimCLR, TS-TCC)가 pretext-based method(SSL-ECG)보다 더 좋은 결과를 냄 -> contrastive method로 feature 학습하는 것이 효과가 있음
• CPC가 SimCLR보다 좋은 결과를 보임 -> temporal features가 general features보다 더 중요함을 보여줌
  

5.2. Semi-Supervised Training

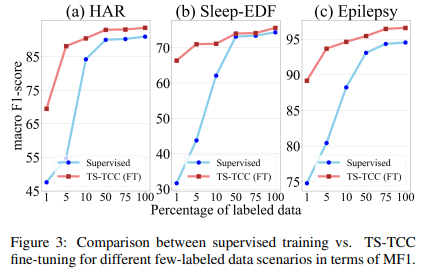
-> few labeled samples에 대해 TS-TCC가 좋은 성능을 보임

5.3. Transfer Learning Experiment

• 하나의 condition에 대해 학습하고 다른 condition에서 테스트
• 약 4%정도 acc가 높음을 확인할 수 있음

5.4. Ablation Study

5.5. Sensitivity Analysis

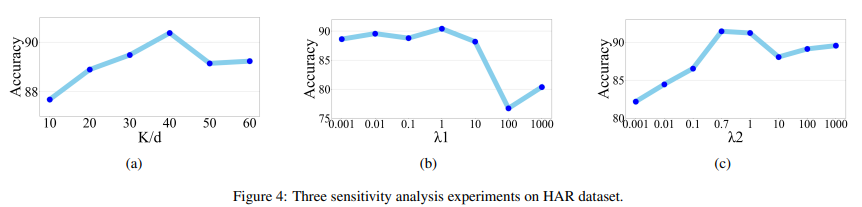
• 파라미터 튜닝: K(예측하려는 time step 수), 람다1, 람다2
• 예측하려는 길이 K가 길수록 ACC 향상이 있지만 일정 값 이상은 다시 ACC가 떨어짐
• 따라서 K를 dx40%로 설정함.

[Q&A]
Q1) Augmentation을 한 시계열이 어떻게 같다고 할 수 있는지?
Time series data는 보이는 이미지적 형태를 사용하는게 아니라 temporal dynamics를 추출해서 사용하니깐 그런게 아닐까 생각이 듦. (Strong aug와 weak aug를 할 때 상관관계가 있지만 형태가 다른 2가지 데이터를 만든다고 해서 이런 추측을 함.) 근데 time series augmentation을 좀 더 공부해봐야 정확히 이해할 거 같음...

Q2) 다른 baseline 모델과 어떻게 결과 비교?
보통 Representation Learning 모델 평가는 고차원인 클래스들의 특성을 저차원(2차원 또는 3차원)으로 줄여서 클래스들 간의 특징을 잘 구분했는지 눈으로 확인하는 manifold 평가 방법을 사용한다고 함
하지만 이 논문에서는 분류 성능을 비교한 건데, self-supervised pre-trained encoder(라고만 써있는데 내 생각엔 representation learning할 때 사용한 파랑색 encoder를 말하는듯)는 고정하고 output linear layer만 fine-tuning해서 사용해서 분류를 진행하고 acc와 f1으로 성능 비교함.

Q3) transformer에 넣기 전에 encoder features와 함께 넣는 c는 무엇인지?
class token에 대한 위치에 있는 정보를 사용한 거라는데, BERT에서 영감을 받아 왔다는 걸 보니 전체 시계열에서 어느 위치쯤에 있는지 말해주는 거라고 생각함

+추가설명

• Temporal Contrasting에서 Contrastive learning이 아니라 cross-view prediction을 하는 것임
• Strong에서 나온 c_t를 이용해 Weak의 z_t+1부터 z_t+k를 예측함. (반대도 마찬가지)
• c_t에 W_k(시점마다 W값이 다름)를 곱해서 (z_t+k)^를 예측함.
• 그리고 그걸 원래 z_t+k와 dot product를 해서 유사도를 계산하는 것임.
• 추가적으로, 이런 유사도를 최대화하는 것을 목적으로 하고 Loss 식이기 때문에 앞에 마이너스를 붙여서 식을 구성함.