What are Diffusion Models?

1. Denoising Diffusion Probabilistic Models (970회 인용)

Ho, J., Jain, A., & Abbeel, P. (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems, 33, 6840-6851.

😎 기존 Diffusion의 문제점이었던 복잡성을 해소함.

• Fixed Noise Scheduling을 최대한 활용해서
• $X_t$ 파라미터를 간소화하고, 불필요한 연산을 제거해서

1_1. Generative Model

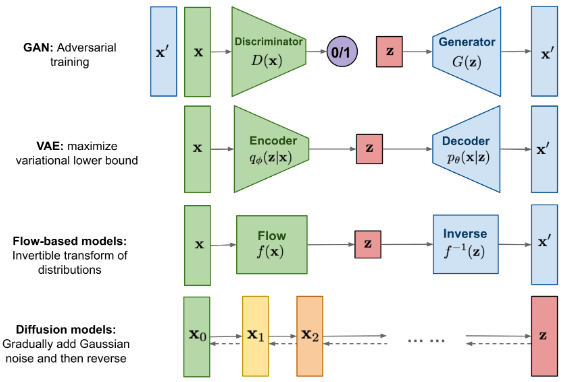
✔ GAN

• Discriminator D와 generator G의 적대적 학습 활용

• Generator를 통해 매우 간단한 분포 z를 특정한 패턴을 갖는 분포로 변환

• 최종적으로 안정적인 학습을 위해서는 Discriminator와 generator가 균형을 띄는 것이 중요함.

  (한계점)

  • 모델 훈련의 불안정성 -> Wasserstein GAN(2017)
  • 성능 평가의 어려움
  • Mode Collapsing 문제 -> AdaGAN(2017), MAD-GAN(2018) 제안됨

✔ VAE

• 학습된 Decoder를 통해 latent variable을 특정한 패턴의 분포로 mapping

• Encoder를 모델 구조에 추가해 Latent variable z를 Encoder를 통해 만듦.

• 최종적으로 Likelihood $p_\theta(\mathbf{x}\vert\mathbf{z})$를 활용해 $p_\theta(\mathbf{z})$를 극대화 하는 것이 중요함.

  (한계점)

  • Density를 직접적으로 구한것이 아니기 때문에 Pixel RNN/CNN 과 같이 직접적으로 Density를 구한 모델보다는 성능이 떨어짐.
  • GAN에 비해 샘플이 흐릿하고 품질이 떨어짐. -> VQ-VAE-2(2019)

✔ Flow-based models

• 심층 신경망 기반 확률적 생성 모형 중 하나

• 잠재 변수(Z) 획득을 위해 변수 변환 공식을 사용함.

  (한계점)

  • Jacobian을 계산할 때 연산이 많이 드는 경우 있음.
  • affine coupling flow들은 충분히 표현력이 강하지 않음. -> Flow++(2019)
  • 변환 함수에 역함수가 존재해야 함.

1_2. Diffusion

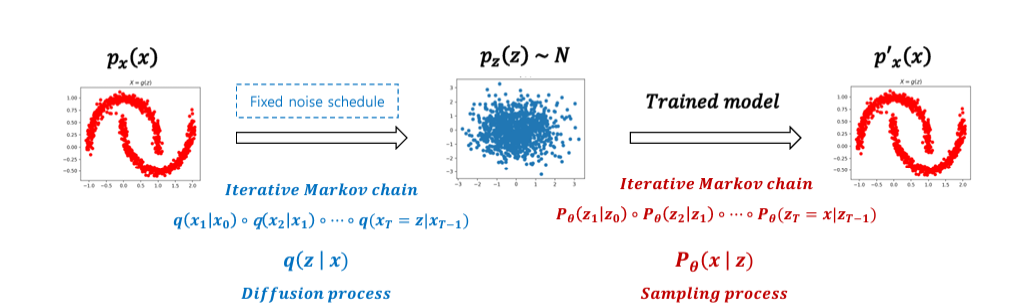
• 학습된 Diffusion model의 조건부 확률 분포 $p_\theta(\mathbf{x}\vert\mathbf{z})$를 통해 특정한 패턴의 분포 학습

• 생성에 활용되는 조건부 확률 분포 $p_\theta(\mathbf{x}\vert\mathbf{z})$을 학습하기 위해 Diffusion process $q(\mathbf{z}\vert\mathbf{x})$를 활용

  [Diffusion Model]

  

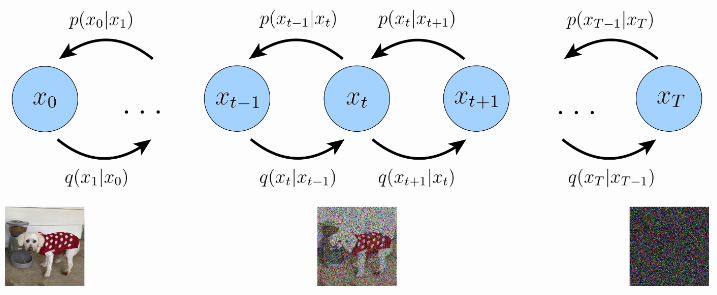
  • Deep Generative Model 중 하나로, data로부터 noise를 조금씩 더해가 패턴을 무너뜨리고 이를 복원하는 개념으로 학습
  • Data로부터 noise를 조금씩 더해가는 forward process(diffusion process)와 이와 반대로 noise로부터 조금씩 복원해가면서 data를 만들어내는 reverse process로 구성됨.
  • 따라서, 2개의 각 Process(Diffusion, Reverse)내 변환 과정은 "Markov Chain"으로 매우 많은 단계로 쪼개져 구성됨.

1_3. Diffusion process (Forward)

: Gausian noise를 점진적으로 주입하는 과정 (=Conditional Gaussian distribution)

• 주입되는 Gaussian noise는 $\beta_t$로 표기하고, Linear schedule, Quad schedule, Sigmoid schedule 3가지 타입을 고려함.
  
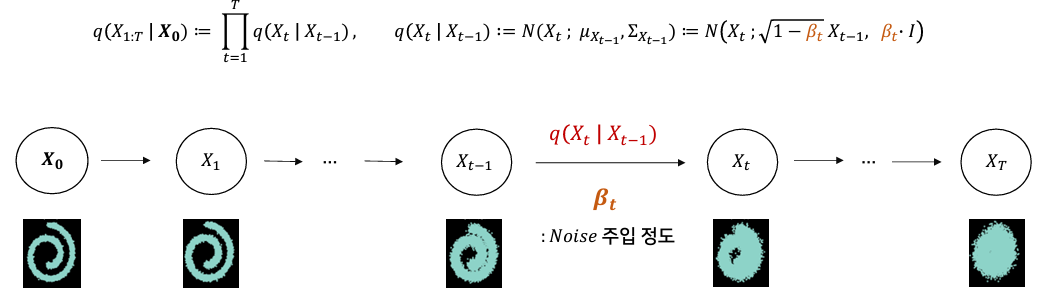
• Conditional Gaussian의 조건부 분포로서, $X_0$로부터 $X_1$...$X_T$를 생성함.
• Markov Chain의 원리를 사용해, 다음 단계($X_{t}$)로 가는데 이전 단계($X_{t-1}$)만을 사용함.
• 최종적으로 가장 마지막 latent variable($X_{T}$)로 'pure isotropic gaussian' 획득.

1_4. Reverse process

: Diffusion process의 역 과정으로, gaussian noise를 제거해가며 특정한 패턴을 만들어가는 과정

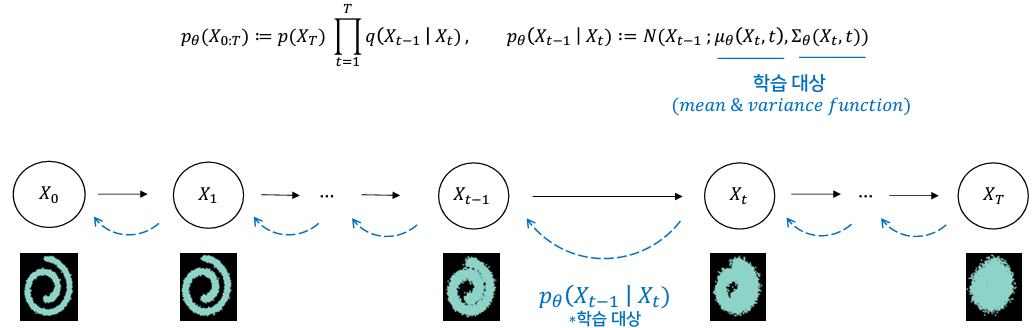
• Diffusion process에서는 어떤 노이즈를 넣는지 알지만, Reverse process에서는 알지 못하기 때문에 "학습"이 필요함.
• 따라서 $p_\theta(\mathbf{X_{t-1}}\vert\mathbf{X_t})$와 유사한 $q(\mathbf{X_{t-1}}\vert\mathbf{X_t, X_0})$를 학습함.

1_5. Denoising Diffusion Probabilistic Models (DDPM)

: 기존 복잡한 Diffusion식을 MSE 식으로 단순화함.

1. 학습 목적식에서 Regularization term 제외함.

   • Regularization term은 gaussian 분포를 따르도록 강제하는 역할을 함.
   • 하지만, Linear noise scheduling을 사용하면 필요한 isotropic gaussian을 확보할 수 있음.

2. Denoising Process의 목적식 재구성

   • 평균과 분산 각각을 추정해야 했지만, $\beta$ 값들로 분산을 상수화함으로써 식을 간소화함.

   • 'Denoising matching'으로 평균 간소화함.

     -> 평균 식에 있는 $x_t$에서 실질적으로 학습해야 할 대상은 $\boldsymbol{\epsilon}$ 뿐임. (아래 식 참고)

     $\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} & \text{ ;where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} & \text{ ;where } \bar{\boldsymbol{\epsilon}}_{t-2} \text{ merges two Gaussians (*).} \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\ \end{aligned}$

     -> 따라서 변형된 $x_t$로 새롭게 목적함수를 정의하면 아래와 같음.
     

   $\begin{aligned} L_t &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \| \color{blue}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \|\boldsymbol{\Sigma}_\theta \|^2_2} \| \color{blue}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}$

   -> 최종적으로 사용한 식은 coefficient term을 제거한 식임.

   $\begin{aligned} L_t^\text{simple} &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}$

1_6. Experiments

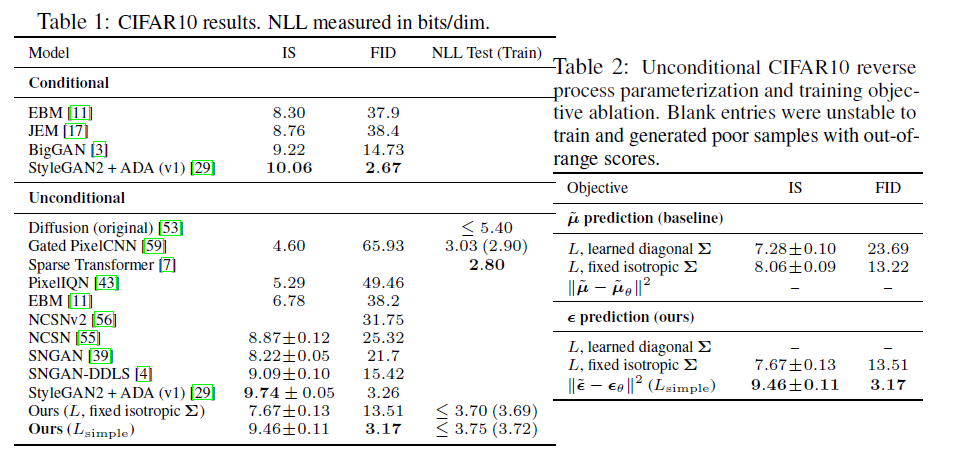
• Table 1을 보면, DDPM이 FID score면에서 월등히 높음.
• Ablation Study 결과인 Table 2를 보면, coefficient term을 제거하면서 FID가 크게 향상됨.
• coefficient term은 각 시점의 noise 크기 $\beta$ 값으로 구성되기 때문에, t가 커질수록 작아짐
  -> 더 noisy한 Loss가 상대적으로 down-weight되는 효과가 발생함.
  -> 따라서, coefficient term을 제거함으로써 모델이 noise가 심한 이미지의 denoising에 집중하도록 유도함.

---

2. AnoDDPM: Anomaly Detection with Denoising Diffusion Probabilistic Models using Simplex Noise (8회 인용)

Wyatt, J., Leach, A., Schmon, S. M., & Willcocks, C. G. (2022). AnoDDPM: Anomaly Detection With Denoising Diffusion Probabilistic Models Using Simplex Noise. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 650-656).

😎 DDPM을 unsupervised anomaly detection에 적용함.

• DDPM은 GAN보다 뛰어난 mode converge를 하며, VAE보다 높은 샘플 퀄리티를 가짐.
• 하지만, DDPM은 긴 Markov chain sequences 때문에 시간과 비용 측면에서 단점이 존재함.
• 따라서 본 논문에서는 Partial Diffusion과 Simplex Noise를 통해 기존 한계점을 극복하고 이상 탐지에 적합한 Diffusion 모델을 제안함.

2_1. Motivation

1. 너무 오래 걸림.
2. Gaussian Noise를 쓰면 너무 성능이 좋아서, 이상도 복원을 해버림.
   -> 따라서 이상 탐지를 하기에 적합하지 않음.

2_2. Proposed Method

1. Partial Diffusion

2. Simplex Noise

1. Partial Diffusion

• Noise를 주는 횟수를 줄임.
• 기존 DDPM은 아예 isotropic gaussian이 될 때까지 Noise를 줌.
• 하지만, Markov Chain을 많이 하는 작업은 시간과 비용이 많이 듦.
• 따라서 본 논문에서는 실험을 통해 최적의 Noise 횟수를 정함.
  -> 고해상도로 복원해내지 않아도 되는 task에서 사용 가능
  (ex- Anomaly Detection)

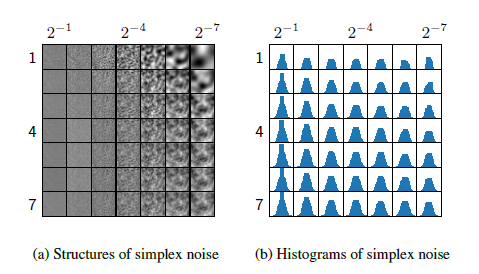
2. Simplex Noise

Diffusion은 모든 부분을 잘 복원하는 것이 핵심임.
-> 따라서, 종모양을 띄는 정규분포를 Noise로 사용함.
-> 즉, 빈도가 높은 곳(정상 부분)에 확률적으로 Noise가 많이 들어가지만, 빈도가 낮은 곳(이상 부분)은 Noise를 적게 줘서 정상과 이상 모두를 잘 복원함.
-> 따라서 Gaussian Noise 대신 Simplex Noise를 도입함.
*Simplex Noise
: 빈도가 낮은 곳도 Noise를 동일하게 주는 것

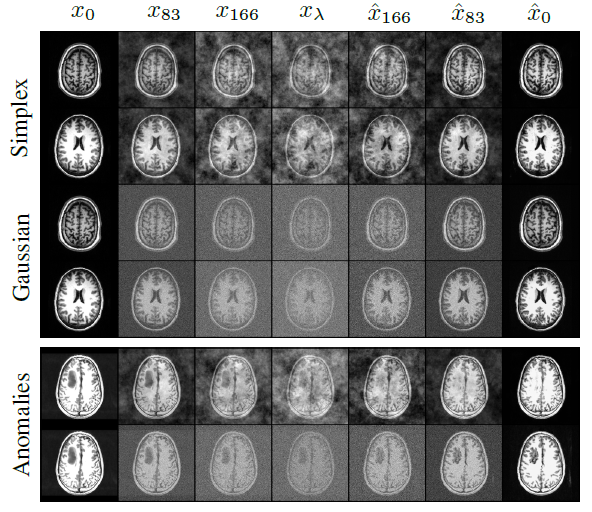
2_3. Experiment

• 2가지 데이터셋에 대해 실험을 진행함.
  - 왼쪽은 MVTec AD leather subset, 오른쪽은 Neurofeedback Skull-Stripped (NFBS)
  - 왼쪽은 서로 다른 이미지에 대해 Gaussina과 Simplex를 적용한 것임.
  - 오른쪽은 하나의 이미지에 대해 simplex noise $v$를 다르게 한 것임.
  

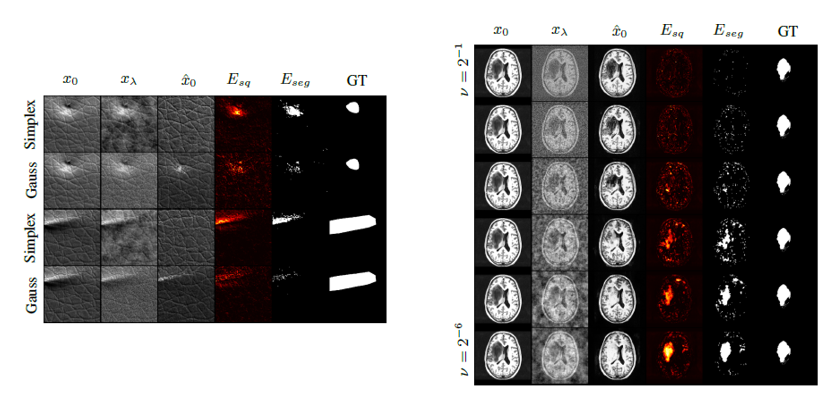
• Gaussian 보다 Simplex를 사용한 것이 더 높은 성능을 보임.
  

• 정상 125개 -> 100개 train, 25개 test / 비정상 22개 -> 22개 test
  -> 적은 데이터셋으로도 학습 가능함

2_4. Future Works

• 한 번 생성하는 것이 아니라, 여러번 생성해서 평균 낸것이 더 좋지 않을까

• 컬러 이미지, 3D 이미지에도 도입해보고자 함.

😅한계점

• Partial Diffusion
  -> 완전히 무너뜨리고 복원하는 것이 아님.
  -> 이러한 특징으로, 원본 데이터와 똑같이 복원함.
  -> 데이터를 다양하게 생성하는 생성 모델 Diffusion의 장점이 사라짐.
  + 데이터셋마다 몇 번의 Noise를 줘야 하는지 다름.

• Simplex Noise
  -> 복원 성능 자체가 떨어짐.
  -> 복원을 잘하는 생성 모델 Diffusion의 장점이 사라짐.

참고 문헌
https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
https://lv99.tistory.com/57 (GAN 관련)
https://blog.naver.com/PostView.naver?blogId=atelierjpro&logNo=220983485213&redirect=Dlog&widgetTypeCall=true&directAccess=false (VAE 관련)
https://drive.google.com/file/d/17kBC7d3x-GfuEevc9N1fb1FeSKUsZ6vY/view (Diffusion 이미지)
https://calvinyluo.com/2022/08/26/diffusion-tutorial.html (Diffusion 이미지)