[통계] 12-2. Simple Linear Regression 단순선형회귀

L·2020년 7월 31일

Quantative Trading

목록 보기

3/9

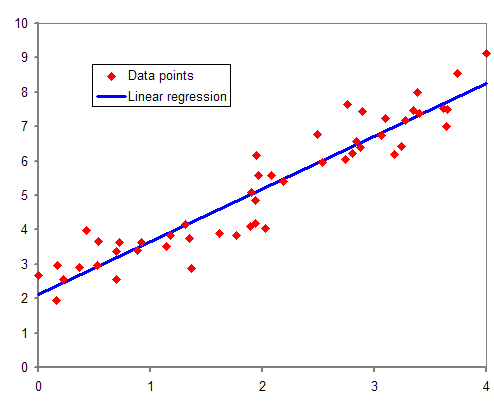
각 1개의 독립변수와 종속변수를 가진 데이터셋을 가정할 때, Data points의 중심을 통과하는 하나의 직선을 상상할 수 있다.

최적의 직선을 찾는 과정이 선형회귀이다.

잔차(residuals)들의 거리가 가장 작은 직선.
* (실제값) - (추정치)

잔차제곱합( $RSS$ : Residual Sum of Square)을 최소로 하는 선

\hat{y} = \beta x + \alpha

RSS = \sum_{i=1}^{n}(Y_i - \hat{Y_i})^2 = \sum_{i=1}^{n}(Y_i - (\beta X_i + \alpha))^2

잔차제곱합을 최소로 만드는 $\beta,\ \alpha$ 를 찾기 위한 대표적인 최소제곱법.
위 식을 $\beta,\ \alpha$ 에 대해 편미분한 값이 0일 때 $RSS$ 가 최솟값이 된다는 미적분학 이론(페르마의 정리)에 의해, 연립방정식을 풀어 최적의 $\beta,\ \alpha$ 값을 찾을 수 있다.

\beta = \frac{\sum_{i=1}^{n}(Y_i - \bar{Y})(X_i - \hat{X_i})}{\sum_{i=1}^{n}(X_i - \bar{X})^2}

\alpha = \bar{Y} - \hat{b_i}\bar{X}