👨💻 회귀 모형의 적합도 판정
회귀 모형의 적합도를 판정한다는 것은, 다시 말해
- 종속변수가 독립변수들로 설명될 수 있는지 (R2)
- 종속변수가 독립변수들로 얼마나 잘 설명되는지 (F 검정)
를 판정하는 일이다.
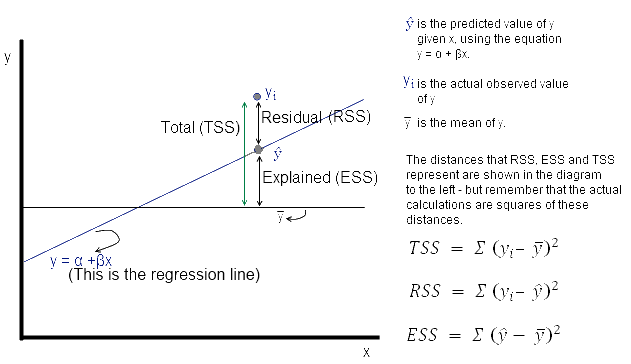
(실제값과 평균의 차이)=(추정치와 평균의 차이)+(잔차)
위 그래프를 통해 직관적으로 알 수 있는 식이다.
이 식을 일반화하여 표현하면 다음과 같다.
(총 변량)=(회귀로 설명가능한 변량)+(회귀로 설명불가한 변량)
위 식을 수식으로 표현하면 다음과 같다.
∣Yi−Yˉ∣=∣Yi^−Yˉ∣+∣Yi−Yi^∣
i=1∑n(Yi−Yˉ)2=i=1∑n(Yi^−Yˉ)2+i=1∑n(Yi−Yi^)2
TSS=ESS+RSS
- TSS: 총 제곱합 Total Sum of Squares = SST
- ESS: 회귀제곱합 Explained Sum of Squares = SSE, SSR(Regression)
- RSS: 잔차제곱합 Residual Sum of Squares = SSR, SSE(Errors)
누군지 몰라도 용어를 참 재미 없게 정의해둔 덕분에 매우 헷갈린다.
🤔 추론
총 제곱합(TSS)에서 회귀제곱합(ESS)이 적당한 비율을 차지할 때,
회귀 모형을 사용하기에 적합한 경우라고 판단할 수 있겠다.
🌟 결정계수 R2
-
회귀 모형의 적합도(goodness of fit)를 판정하는 데 사용되는 계수
결정계수 R2=TSSESS=1−TSSRSS
0≤R2≤1
-
R2=1일 때, X와 Y는 완벽한 비례 관계에 있으므로 회귀분석 불필요.
-
R2=0일 때, X와 Y는 완벽히 무관하므로 회귀분석 불가능.
0<R2<1일 때,
X에 대해 Y를 회귀분석하기에 적합하다고 할 수 있다.
👨💻 F 검정
F 검정의 가설
H0: Y는 X에 대한 회귀식으로 설명할 수 없다.
H1: Y는 X에 대한 회귀식으로 설명 가능하다.
F score
F score=MSEMSR=Mean Square due to ErrorMean Square due to Regression
=RSS/n−pESS/p−1
(n은 표본의 개체 수, p는 독립변수(설명변수)의 수)
F score는 확률 이론에 따라 자유도가 (p−1,n−p)인 F 분포를 따른다.
✍ F 검정의 결론
F 검정의 p-value가 0.05 미만일 때, 귀무가설 H0는 기각되고,
'Y는 X에 대한 회귀식으로 설명 가능하다'는 대립가설 H1이 채택되며,
최종적으로 추정된 회귀식은 적합하다는 결론이 도출된다.
📚 References
Regression Analysis | Risk Prep
Explained Sum of Squares (ESS) | Wikipedia
Residual Sum of Squares (RSS) | Wikipedia
선형 회귀 분석 | 예제와 함께하는 쉬운 통계
