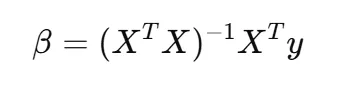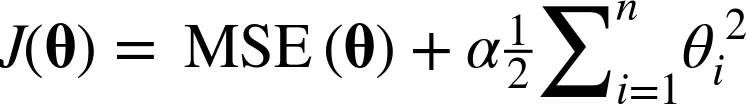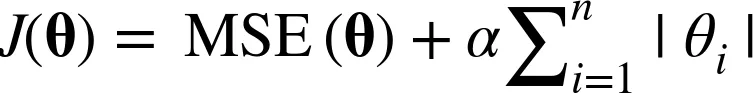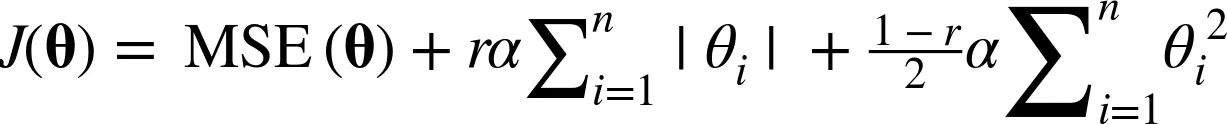[세션] 머신러닝 지도학습 회귀분석

회귀(regression)

• 데이터를 기반으로 연속적인 값을 예측하는 머신러닝 기법
  
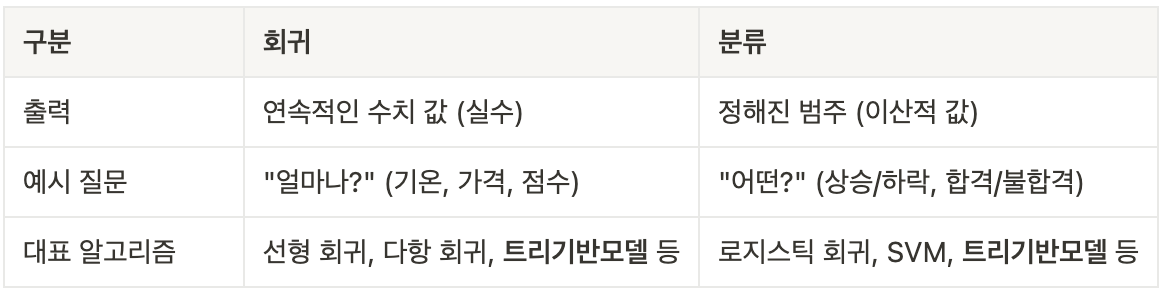
• 분류와의 차이점 : 분류는 범주(categorical) 예측, 회귀는 수치(numerical) 예측

선형 회귀 모델

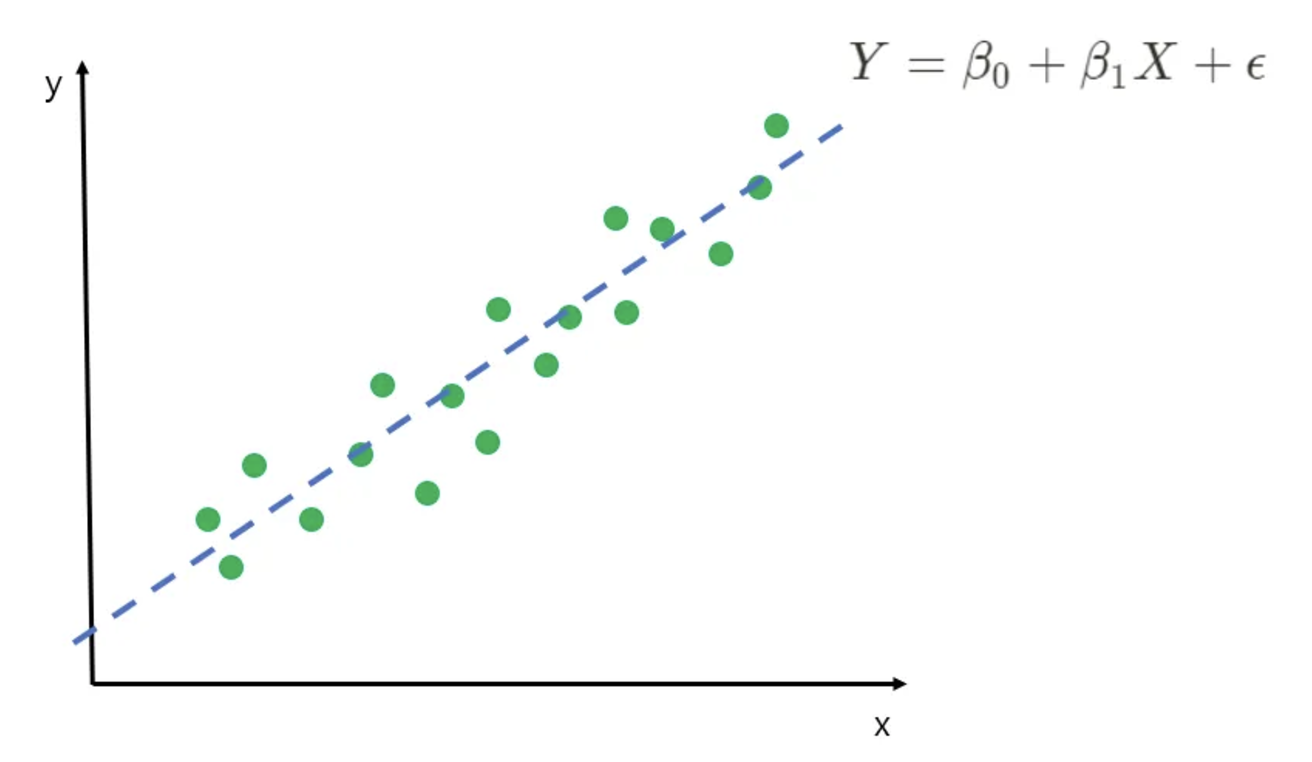
• 독립 변수(입력) X와 종속 변수(출력) Y 사이의 선형 관계를 학습하는 모델
  
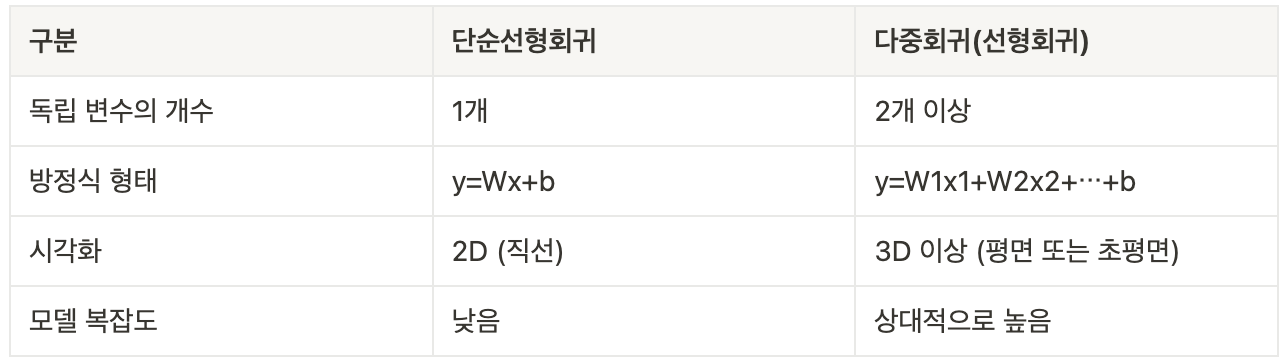
• 다중 선형 회귀 : 독립변수(X)가 여러개 일 때 사용
  
• 모델 학습 과정
  • 손실 함수(오차) : 평균 제곱 오차(MSE)
  • 최적화
    • 수학적 방법 : 오차를 최소화 하는 계수를 찾는 방법인 ‘최소자승법(Ordinary Least Squares)를 사용, sklearn 디폴트 값
      
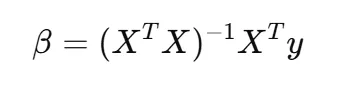
    • 경사하강법 : 경험적으로 오차를 최소화 하는 계수를 찾아냄, sklearn으로 이를 사용하고 싶으면 SGDRegressor를 사용하면 가능
      
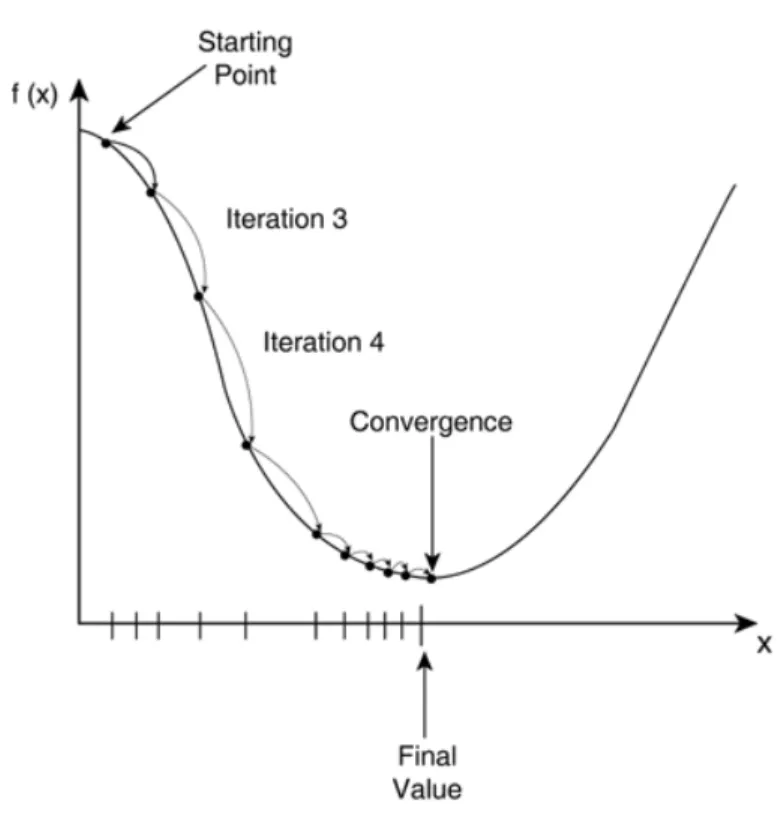
• 한계점 : 비선형 데이터에는 적합하지 않고, 과적합의 위험을 조심해야 함

코드

• 단순 선형 회귀

# 라이브러리
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 데이터 준비
X = [[1], [2], [3], [4], [5]]
y = [2, 4, 6, 8, 10]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 모델 학습
model = LinearRegression()
model.fit(X_train, y_train)

# 예측 및 평가
y_pred = model.predict(X_test)
print("MSE:", mean_squared_error(y_test, y_pred))

• 다중 회귀

# 라이브러리
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

# 데이터 생성
# 독립 변수 (x1, x2)
X = np.array([[1, 2], [2, 3], [3, 5], [4, 6], [5, 8]])
# 종속 변수 (y)
y = np.array([3, 5, 7, 9, 11])

# 학습 데이터와 테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 모델 학습
model = LinearRegression()
model.fit(X_train, y_train)

# 결과 확인
print("회귀 계수 (W):", model.coef_)
print("절편 (b):", model.intercept_)

# 예측
y_pred = model.predict(X_test)
print("예측 값:", y_pred)

• 다중회귀 with 경사하강법

# 라이브러리
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 1. 데이터 준비
X = [[1, 2], [2, 3], [3, 5], [4, 6], [5, 8]]  # 독립 변수
y = [3, 5, 7, 9, 11]                           # 종속 변수

# 2. 데이터 분리 (훈련/테스트 데이터셋)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 3. 데이터 표준화
scaler = StandardScaler()  # SGD는 표준화된 데이터에서 더 잘 작동
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 4. 모델 학습
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, random_state=42, learning_rate='optimal')
sgd_reg.fit(X_train, y_train)

# 5. 예측
y_pred = sgd_reg.predict(X_test)

# 6. 평가
mse = mean_squared_error(y_test, y_pred)
print("회귀 계수 (W):", sgd_reg.coef_)  # 학습된 계수
print("절편 (b):", sgd_reg.intercept_)  # 절편
print("테스트 데이터 MSE:", mse)

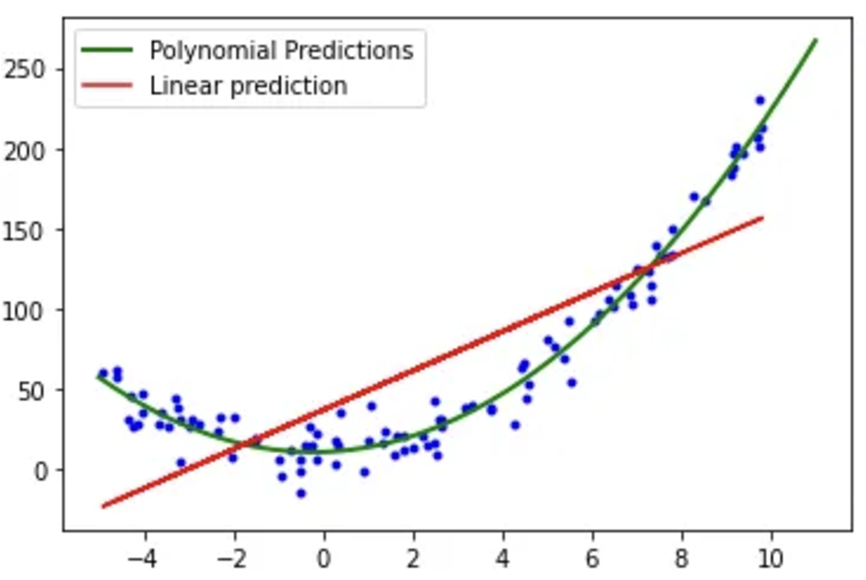
• 다항 회귀(Polynomial Regression) : 비선형 데이터에 사용
  

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np

# 데이터 생성
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([1.5, 4.2, 9.3, 16.8, 25.1])

# 다항 특징 생성 (2차 다항식)
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)

# 모델 학습
poly_reg = LinearRegression()
poly_reg.fit(X_poly, y)

# 예측
y_pred = poly_reg.predict(X_poly)

# 결과 출력
print("다항 회귀 계수:", poly_reg.coef_)
print("절편:", poly_reg.intercept_)
print("MSE:", mean_squared_error(y, y_pred))

과적합 방지용 규제(regularization)를 사용하는 회귀

• 오버피팅을 방지하기 위해 사용하는 것
• 릿지(Ridge) : 제곱으로 추가
  

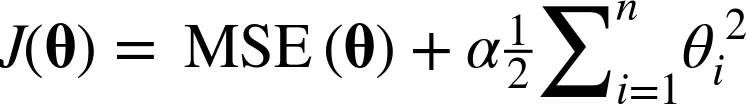
from sklearn.linear_model import Ridge

# 모델 학습
ridge_reg = Ridge(alpha=1.0)
ridge_reg.fit(X, y)

# 예측
y_pred = ridge_reg.predict(X)

• 라쏘(Lasso) : 절댓값으로 추가
  

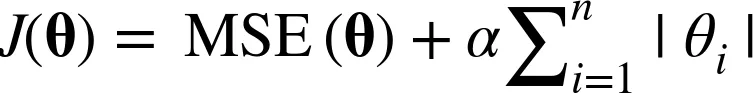
from sklearn.linear_model import Lasso

# 모델 학습
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)

# 예측
y_pred = lasso_reg.predict(X)

• 엘라스틱넷(Elasticnet) : 둘다 추가
  

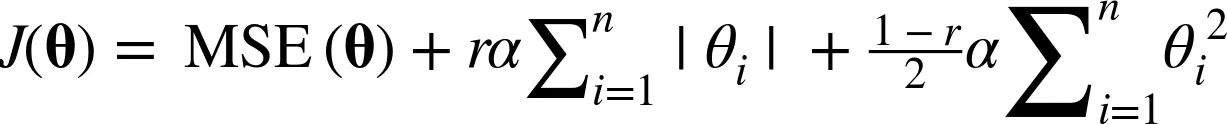
from sklearn.linear_model import ElasticNet

# 모델 학습
elastic_net_reg = ElasticNet(alpha=0.1, l1_ratio=0.5)  # l1_ratio=0.5: L1과 L2의 균형
elastic_net_reg.fit(X, y)

# 예측
y_pred = elastic_net_reg.predict(X)

성능 좋은 회귀

• RandomForest

from sklearn.ensemble import RandomForestRegressor

# 모델 학습
rf_reg = RandomForestRegressor(n_estimators=100, random_state=42)
rf_reg.fit(X, y)

# 예측
y_pred = rf_reg.predict(X)

• XGB (별도의 패키지 설치 필수)

from xgboost import XGBRegressor

# 모델 학습
xgb_reg = XGBRegressor(n_estimators=100, learning_rate=0.1, random_state=42)
xgb_reg.fit(X, y)

# 예측
y_pred = xgb_reg.predict(X)

• Light GBM (별도의 패키지 설치 필수)

from lightgbm import LGBMRegressor

# 모델 학습
lgbm_reg = LGBMRegressor(n_estimators=100, learning_rate=0.1, random_state=42)
lgbm_reg.fit(X, y)

# 예측
y_pred = lgbm_reg.predict(X)

• Catboost (별도의 패키지 설치 필수)

from catboost import CatBoostRegressor

# 모델 학습
catboost_reg = CatBoostRegressor(iterations=100, learning_rate=0.1, depth=6, verbose=0, random_state=42)
catboost_reg.fit(X, y)

# 예측
y_pred = catboost_reg.predict(X)

# 결과 출력
print("CatBoost 예측 값:", y_pred)
print("MSE:", mean_squared_error(y, y_pred))