SPS LAB 2025.02.06 신입생 세미나 3주차
- 본 내용은 Michigan University의 Deep Learning for Computer Vision 7강 Convolutional Networks 강의를 듣고 정리한 내용입니다.
- 강의의 원본은 해당 링크에서 확인하실 수 있습니다.
1. Components of Network
Fully-Connected Network

- Fully-Connected Layers
- Activation Function
Convolutional Network
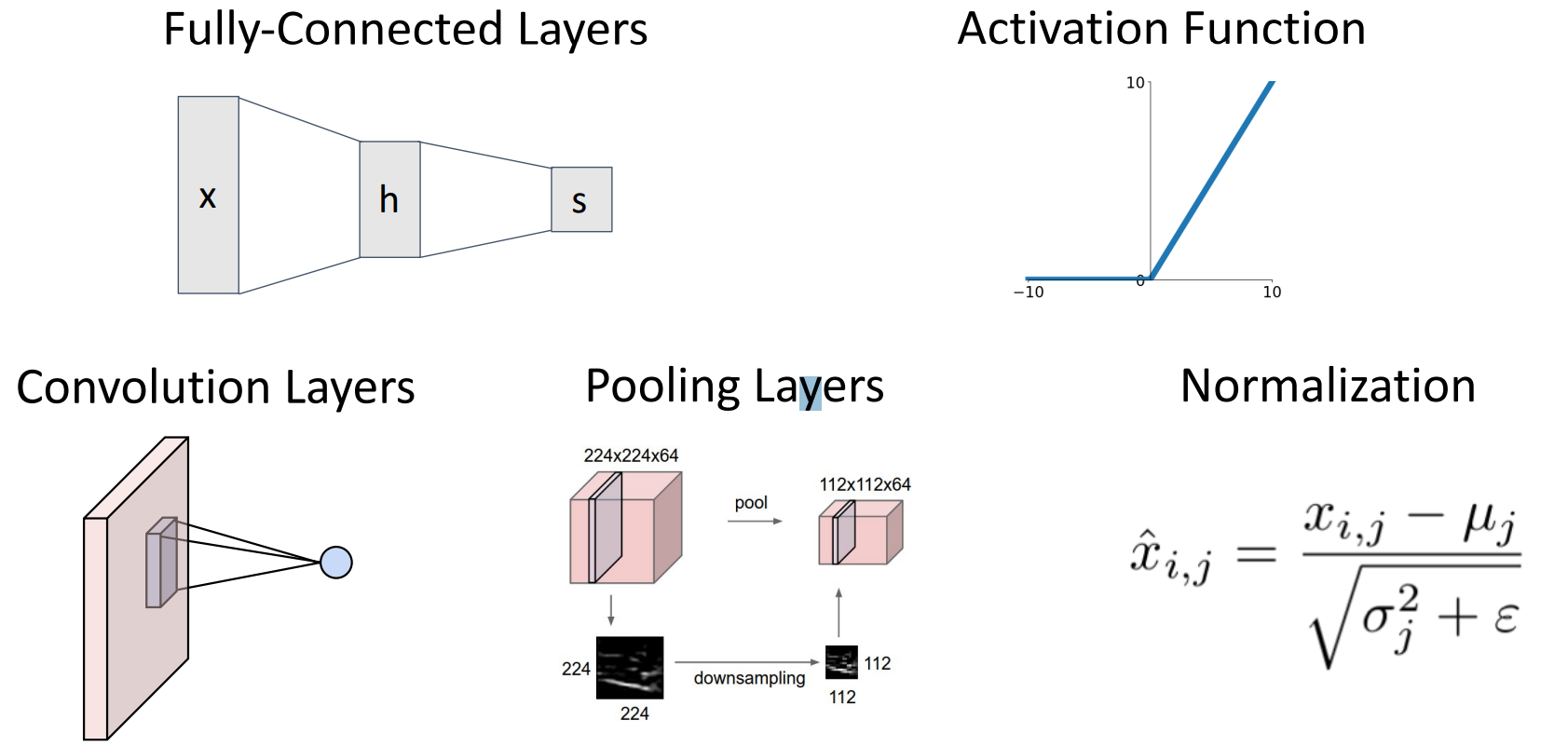
- Fully-Connected Layers
- Activation Function
- Convolution Layers
- Pooling Layers
- Normalization Layers
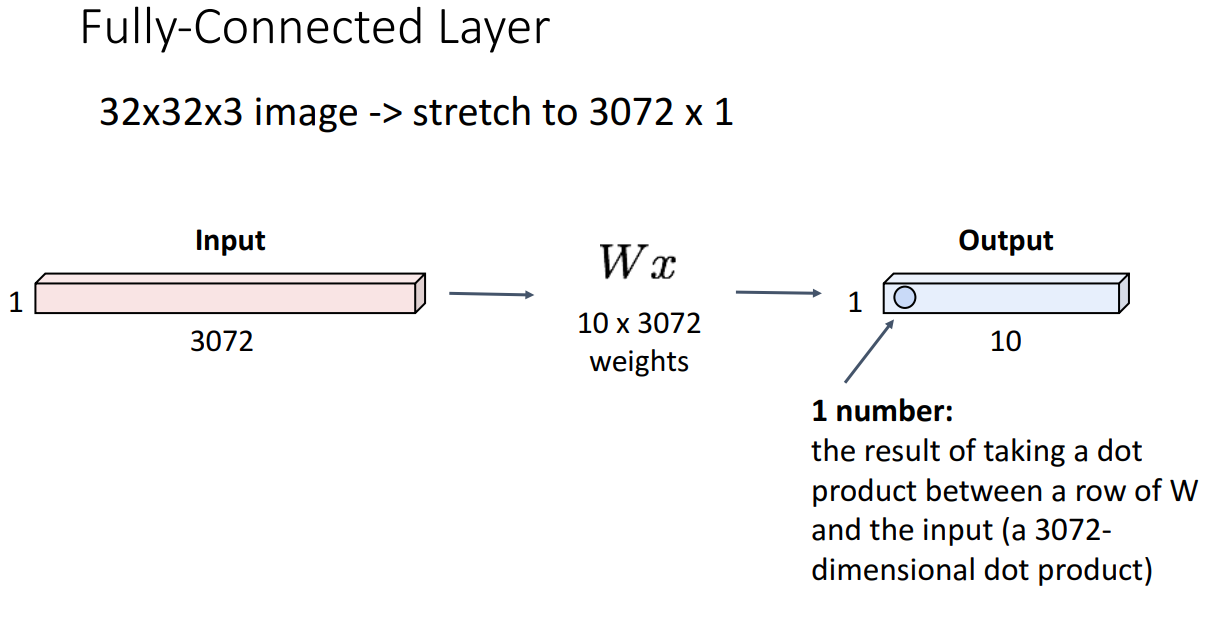
2. Fully-Connected Layer
- 역할: 32 x 32 x 3 image를 3072 x 1로 shape 변경 (벡터화 진행)
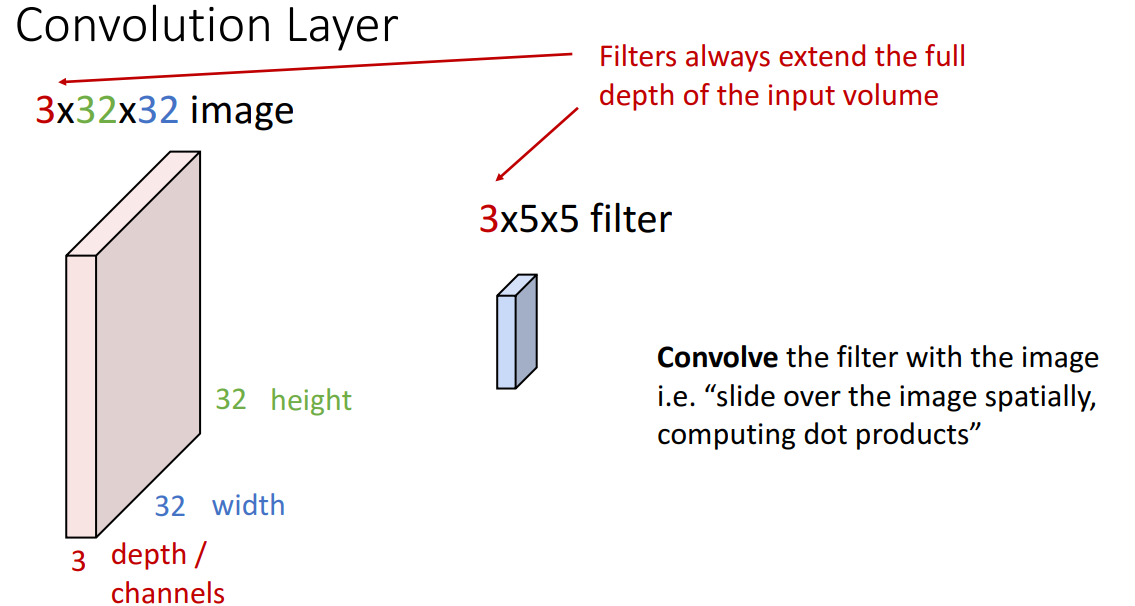
3. Convolutional Layer
-
역할
- stretch된 벡터가 아닌 depth(channel) x width x height의 3차원 벡터를 사용하여 spatial structure를 보존
-
filter
- weight matrix의 역할
- 아이디어: 합성곱 필터를 통해 입력 이미지의 모든 위치로 밀어서 다른 3차원을 계산
- 반드시 input image의 channel과 filter의 channel이 같아야 함
-
첫번째 filter (blue filter)
- input tensor와 filter 사이의 내적곱 진행
- output
- 단일 스칼라 숫자가 출력
- 입력 image의 이 위치가 하나의 필터와 얼마나 일치하는지 효과적으로 알려줌

-
두번째 filter (grren filter)
- blue filter와 다른 가중치를 가진 필터로 내적곱 진행하여 새로운 1 x 28 x 28의 activation map을 얻음
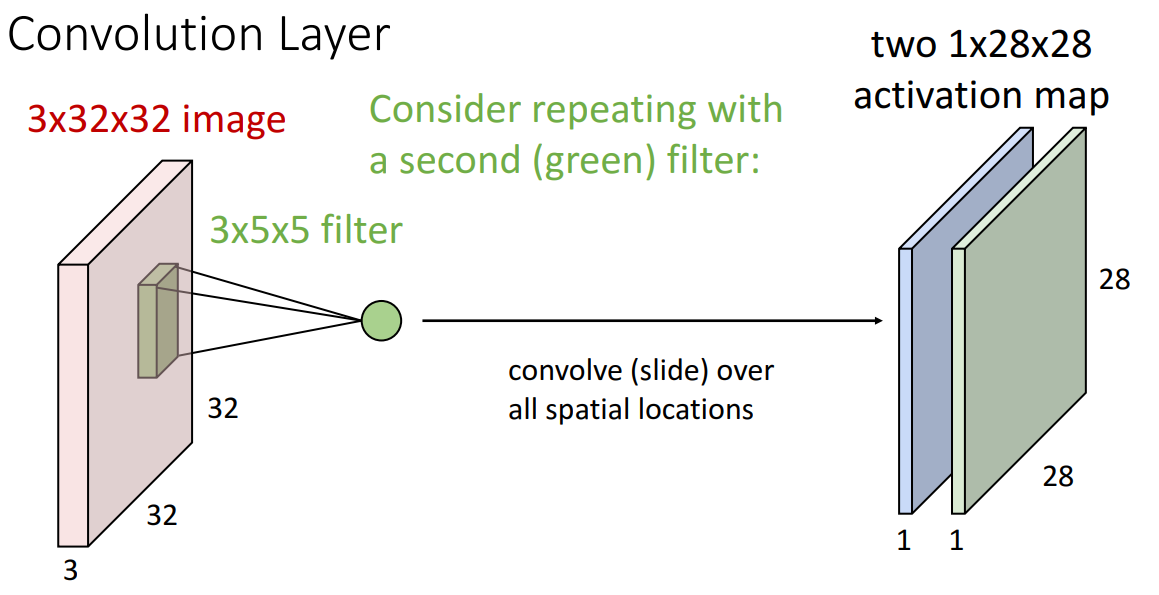
- blue filter와 다른 가중치를 가진 필터로 내적곱 진행하여 새로운 1 x 28 x 28의 activation map을 얻음
-
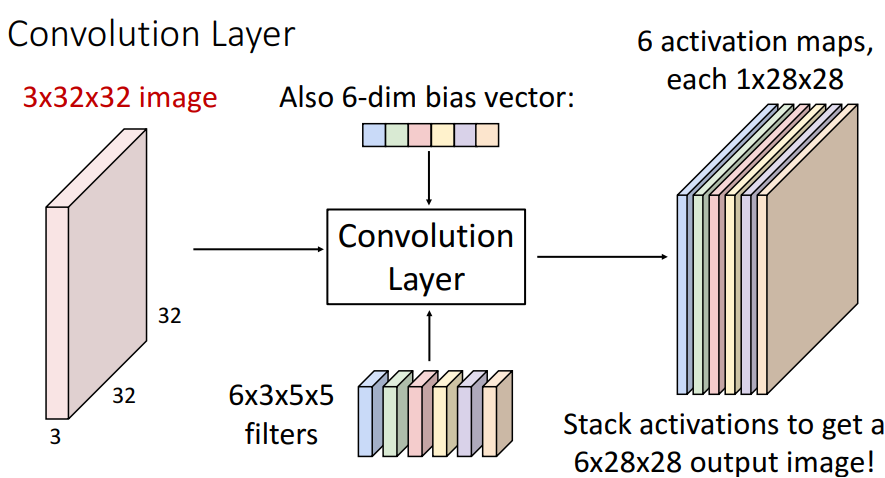
6개의 filter 활용 (filter의 수는 하이퍼파라미터)
- 각 필터의 크기는 3 x 5 x 5
- filter 수는 6개이므로 필터를 모으면 4차원 텐서가 됨 (6 x 3 x 5 x 5)
- 각 필터를 입력 이미지와 합성하면 activation map을 하나씩 얻게 되므로 최종적으로 쌓으면 6 x 28 x 28 3차원 텐서를 얻을 수 있음 (기존 3 x 32 x 32의 3차원 텐서를 6 x 28 x 28의 3차원 텐서로 변환)
-
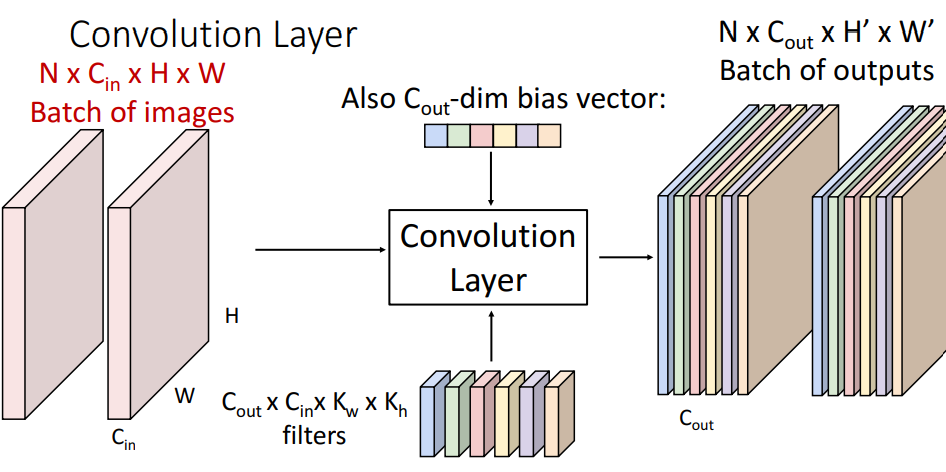
단일 3차원 Tensor들의 모음인 Batch에 적용하는 경우
- N: 배치의 수, C_out: filter의 수, H': Batch마다의 Height, W': Batch마다의 Width
- 배치의 각 요소를 독립적으로 각 필터로 처리
4. Stacking Convolutions
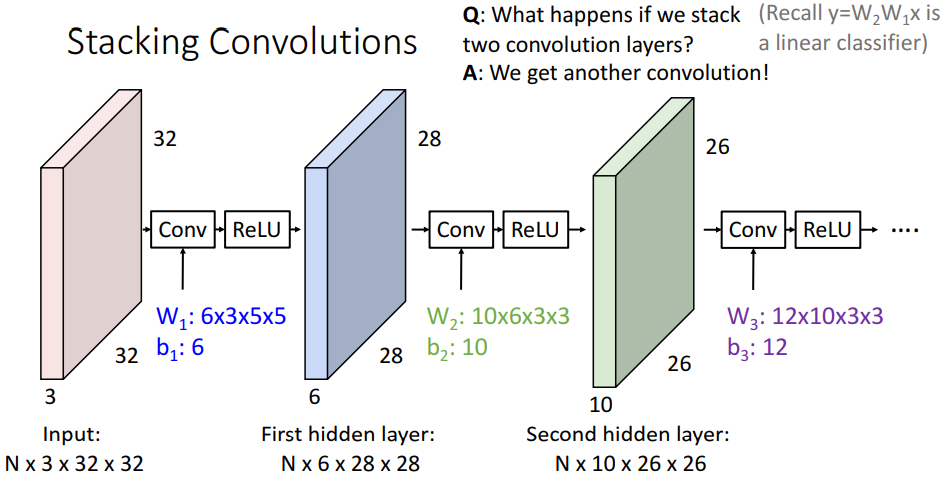
- Convolution layer를 쌓는 것
- 합성곱 층을 쌓기만 하면 합성곱 연산 자체가 선형 연산자이므로 쌓기만 하는 것은 선형 연산자와 별반 다를 게 없음
- 이 문제를 해결하기 위해 합성곱 층 사이에 비선형 활성화 함수를 삽입하여 비선형성 반영
- 주의점은 input image와 filter의 channel이 같아야 함
5. What do convolutional filters learn?
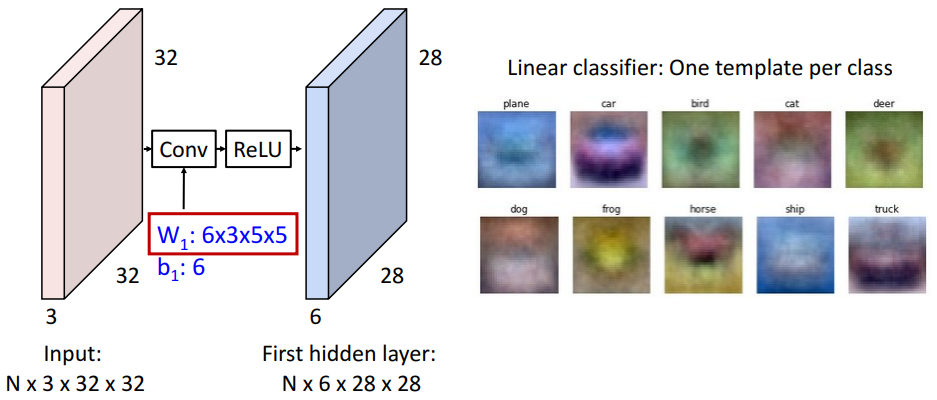
linear classifer
- 클래스 당 하나의 template 학습
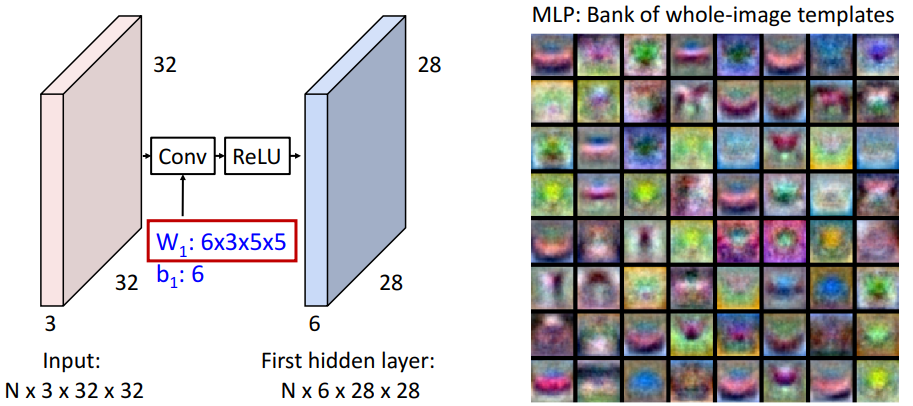
MLP
- 입력 이미지와 동일한 크기를 갖는 template의 Bank 학습
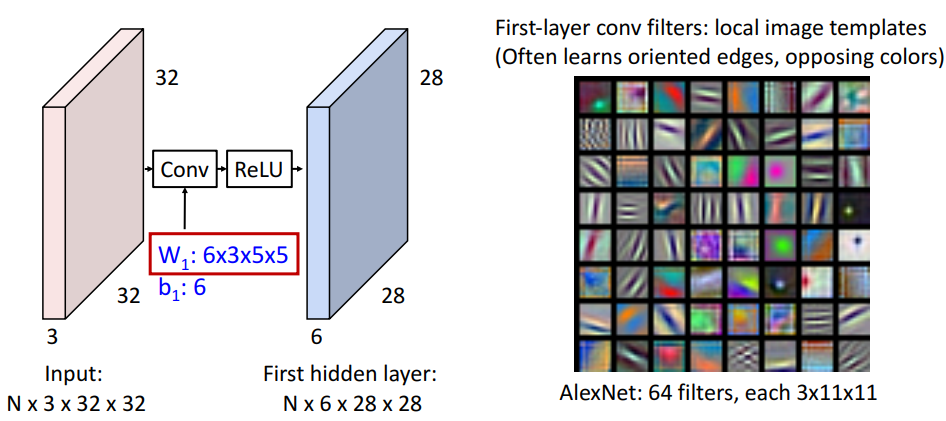
First-layer conv filters
- 전체 입력 이미지와 같은 크기의 템플릿 세트를 학습하는 대신에 작고 지역적인 크기의 템플릿 세트를 학습
- 보통 oriented edge, opposing colors를 학습
- 각 activation map은 입력 이미지의 각 위치가 필터에 응답하는 정도를 제공
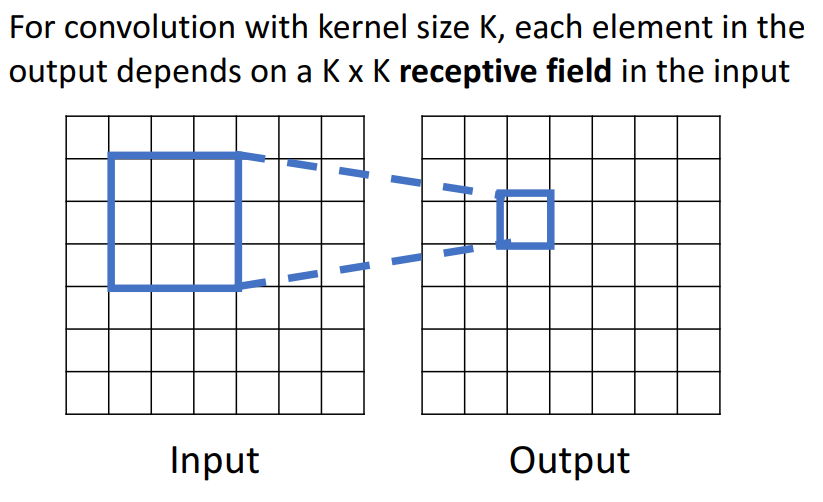
6. Receptive Fields
-
1개의 conv layer
- 오른쪽의 output grid는 왼쪽의 input grid의 로컬 영역에만 의존한다는 것을 의미
- 각 출력값의 요소는 해당 3 x 3의 영역에만 의존
-
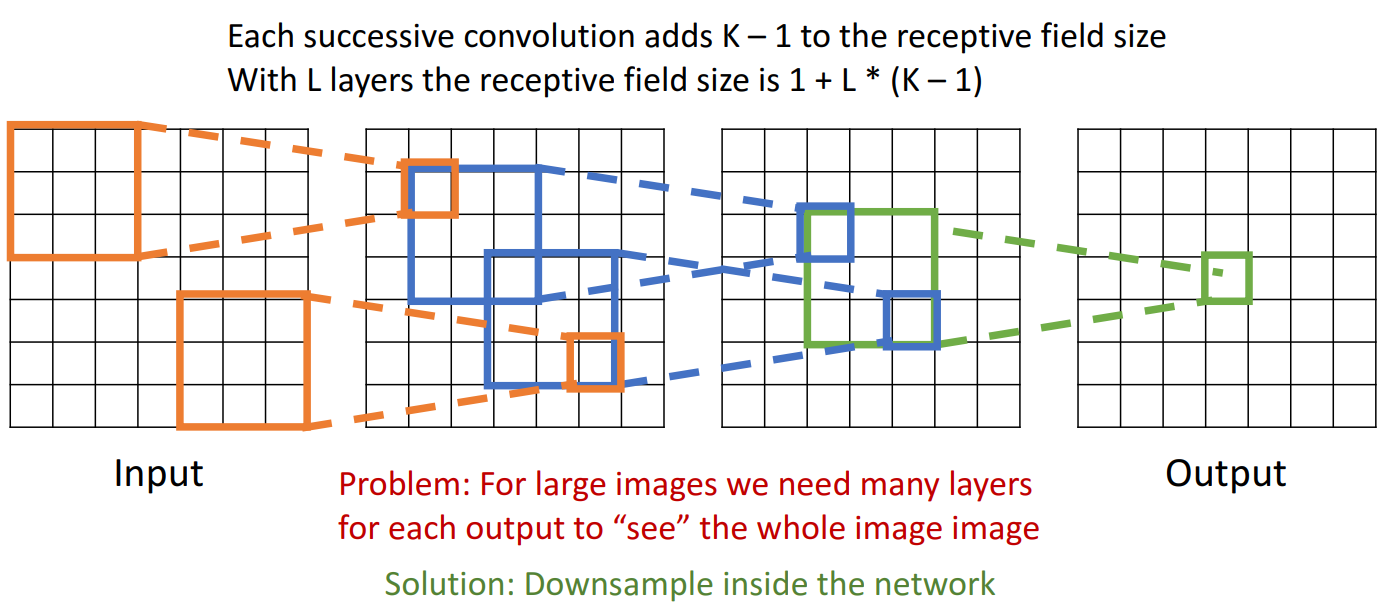
여러 개의 conv layer
- 3개의 합성 레이어가 쌓여 있는 해당 예시에서 output의 각 요소는 input 요소에 따라 달라짐
- Receptive Field의 2가지 의미
- receptive field in the input: 여러 개의 합성곱층을 거치지만, output 해당 요소에 input image가 미치는 영향, 입력 이미지의 공간 크기
- receptive field in the previous layer: 이전 층이 미치는 영향
7. A closer look at spatial dimensions
-
filter
- 계산
- input image: 7 x 7 (W)
- filter: 3 x 3 (K)
- output: 5 x 5 (W - K + 1)
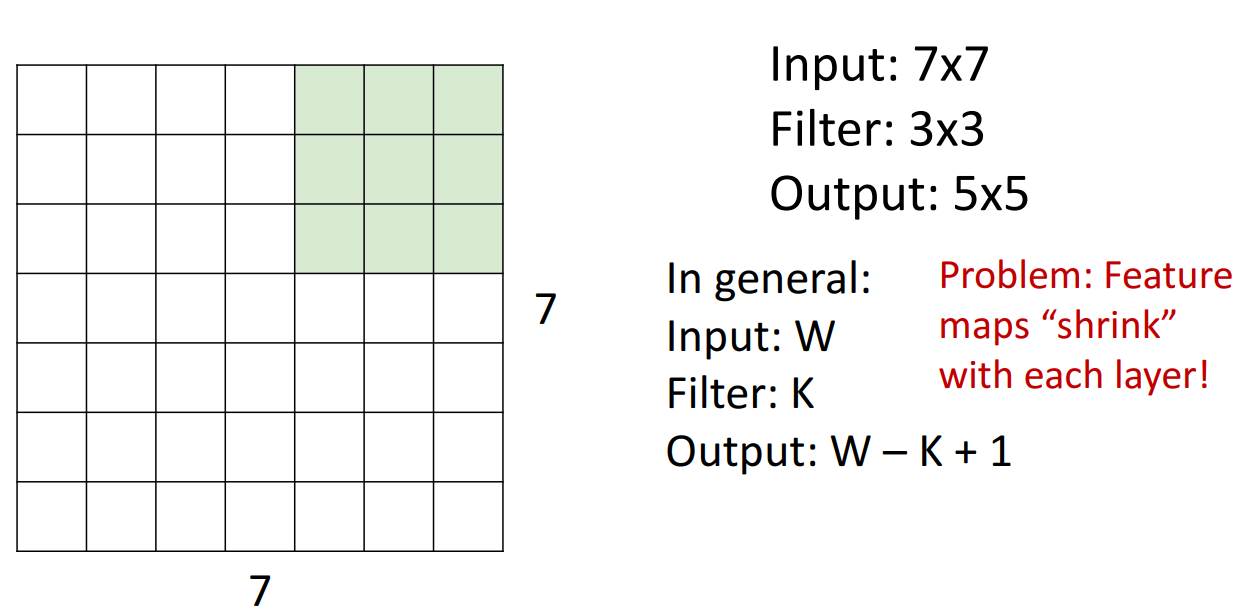
- 계산
-
padding
- 문제점: filter만 있는 경우, Layer를 지나면 지날수록 dimension이 작아지는 문제 --> padding 적용
- 합성 연산을 수행하기 전에 이미지 테두리 주위에 여분의 패딩을 추가하는 것으로, 다시 입력과 동일한 차원을 출력
- 채우는 값에 따라 다양한 전략이 존재
- ex) 0이면 zero padding
- 계산
- input image: 7 x 7 (W)
- filter: 3 x 3 (K)
- padding: P
- output: 7 x 7 (W - K + 1 + 2P)
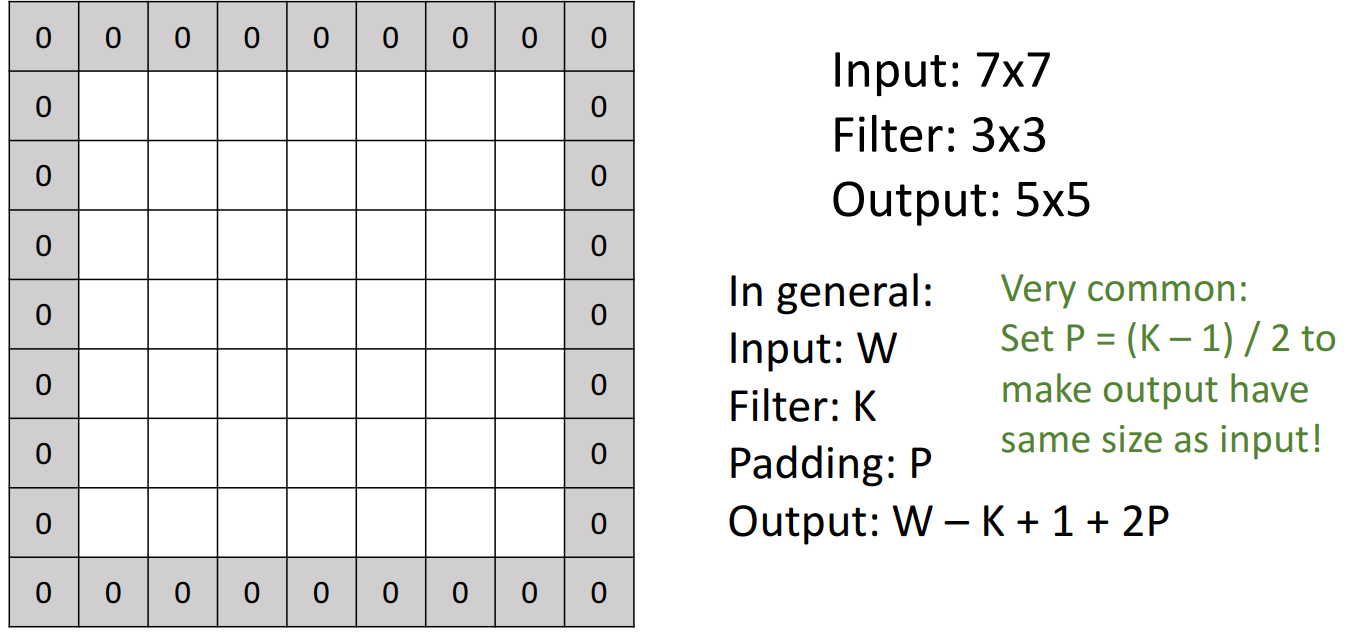
-
stride
- 문제점: 높은 해상도를 가진 이미지를 작업하고 싶다면 고해상도 입력 이미지에서 큰 영역을 볼 수 있는 기능을 갖추기 위해 매우 많은 conv layer를 쌓아야 함 --> stride 적용
- 모든 위치에서 합성곱 연산하는 것이 아니라 Stride 값만큼 떨어진 공간에서 합성곱 연산 진행
- 출력이 상당히 downsample되며, receptive field를 빠르게 구축할 수 있음
- 계산
- input image:7 x 7 (W)
- filter: 3 x 3 (K)
- padding: P
- stride: S
- output: 3 x 3 ((W - K + 1 + 2P) / (S + 1))
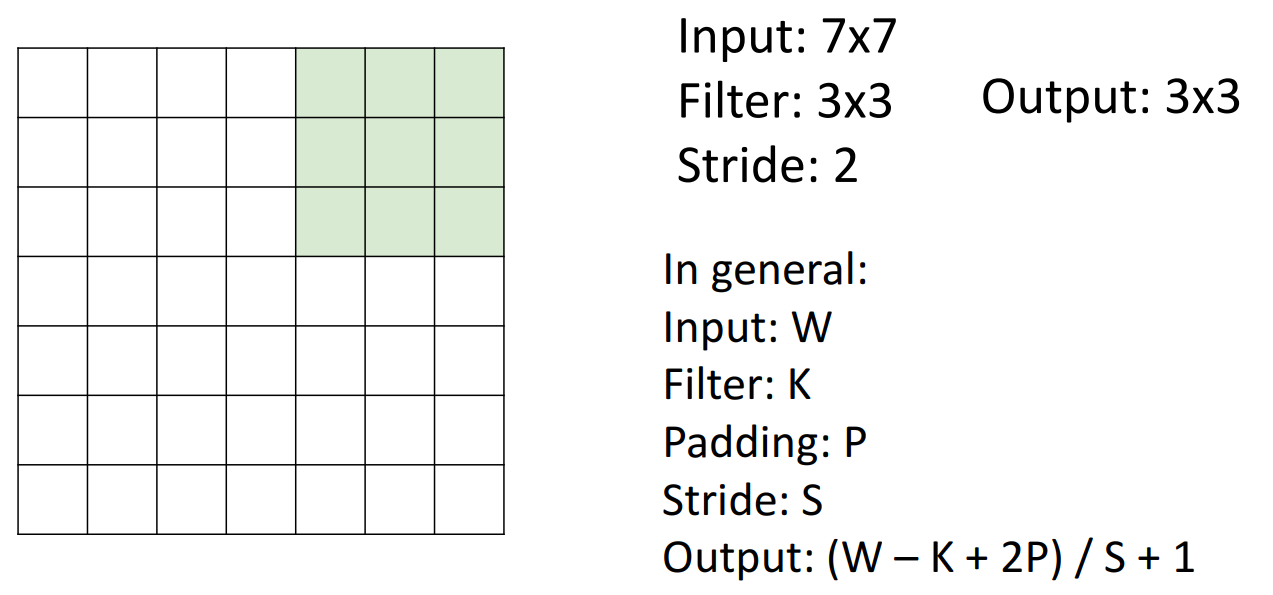
-
예시

8. Convolution Summary

9. Other types of convolution
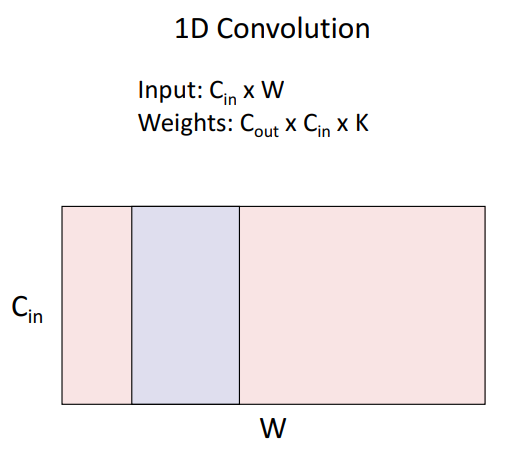
지금까지는 2차원 공간의 모든 위치에서 움직이는 합성곱(2D Convolution) 확인했는데, 다른 유형의 합성곱도 다수 존재
- 1D Convolution
- 3D Convolution
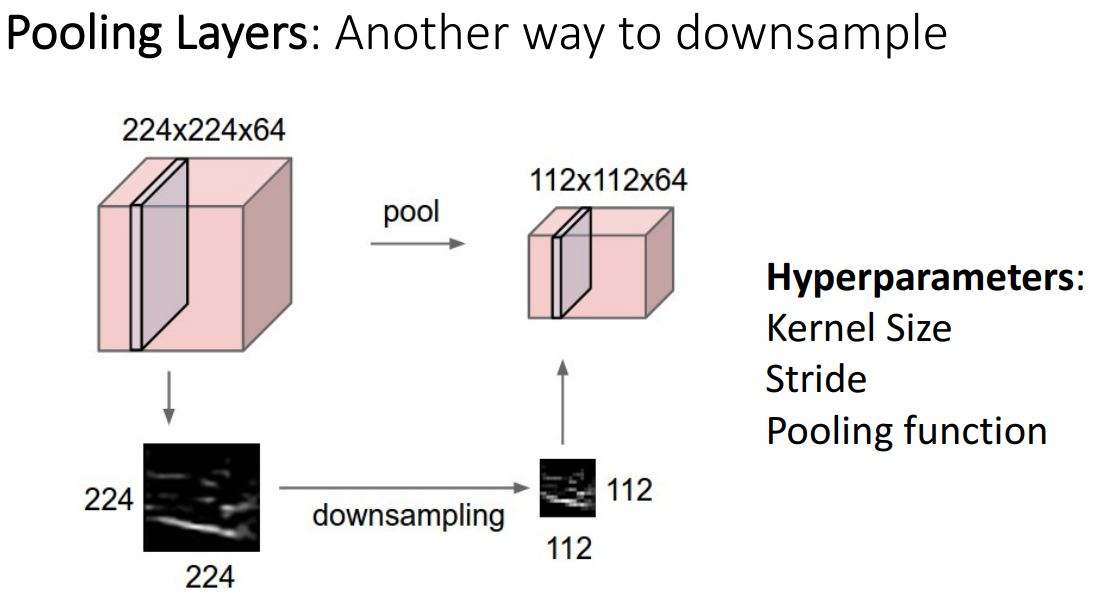
10. Pooling Layer
- 신경망 내부에서 다운 샘플링하는 또 다른 방법으로, 학습 파라미터가 없음
- 대표적인 예시: 2 x 2 Max Pooling
- kernel size와 stride가 같으면 풀링 영역이 겹치지 않음
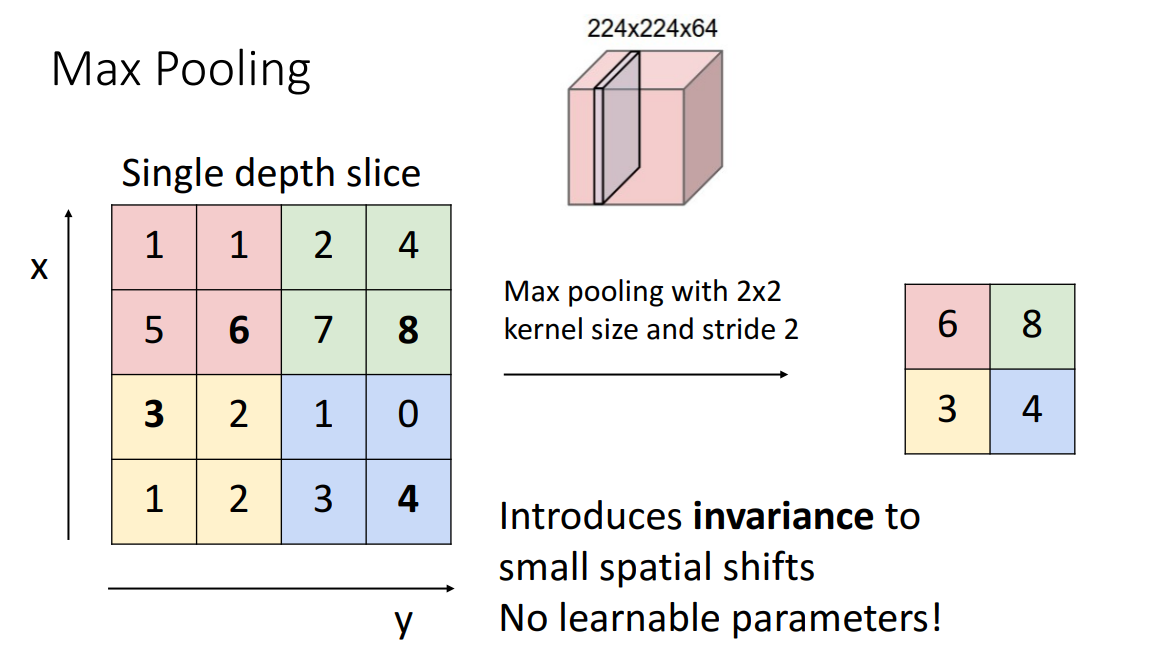
- kernel size와 stride가 같으면 풀링 영역이 겹치지 않음
- pooling이 stride보다 선호되는 이유
- 매개변수에 대한 학습이 필요없음
- Max Pooling이 각 영역 내에서 가장 큰 값을 선택하기 때문에 변환에 어느 정도의 불변성을 가지고 있음
11. Pooling Summary

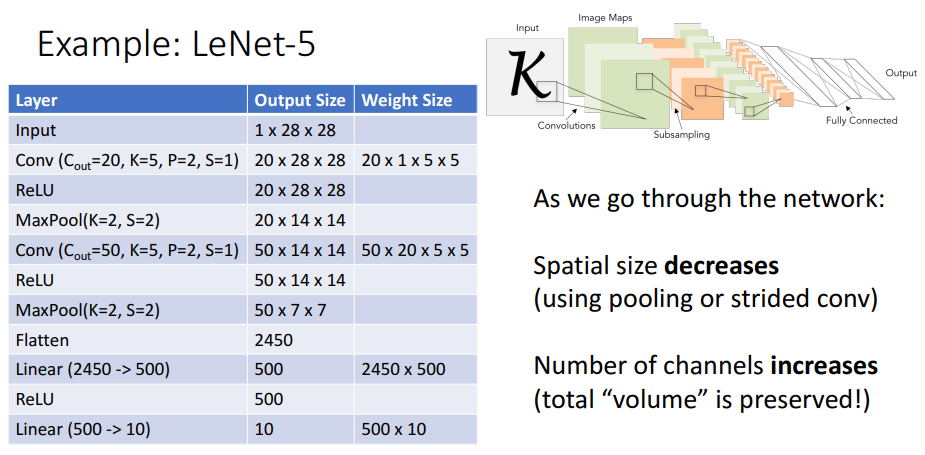
12. Convolutional Networks
- 많은 하이퍼파라미터와 다양한 유형의 레이어가 있기 때문에 합성곱 네트워크를 구현하는 데 많은 자유가 있음
- 대표적인 예시로 LeNet-5가 있음
13. Batch Normalization
- 개념
- 이전 layer에서 나온 출력이 평균이 0이고 분산이 1인 분포를 갖도록 Normalize하는 것
- internal convariate shift(훈련 과정에서 각 층마다 입력 분포가 변하는 것)를 줄이고, 이를 통해 딥러닝 네트워크의 최적화 프로세스를 안정화
- 수식
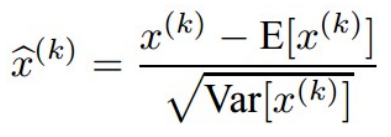
- 구체적 수식
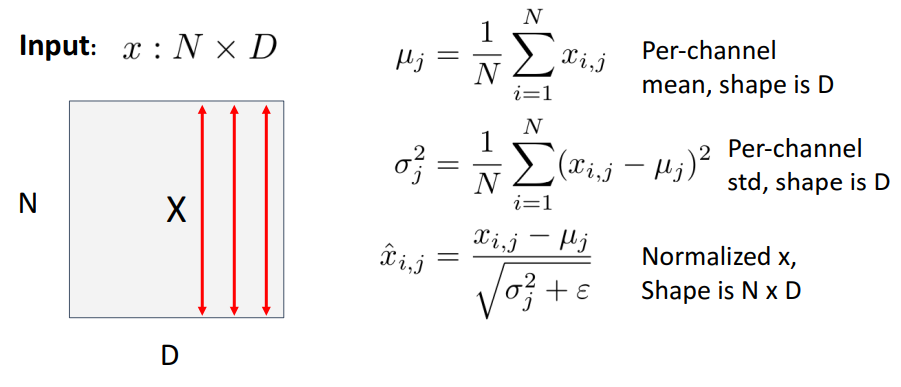
- 문제점 1
- 배치 정규화(Batch Normalization)는 입력 데이터를 평균 0, 분산 1로 정규화하는 기법인데, 이러한 강한 정규화(Zero-Mean, Unit-Variance) 가 오히려 신경망의 학습에 방해가 될 수도 있음
- 문제점 1의 해결책
- 배치 정규화 후 학습 가능한 두 개의 매개변수 𝛾와 𝛽를 도입하여 원래 입력값(Identity function)을 회복시켜줌
- γ (Scale parameter): 정규화된 값의 분포를 조정하여 신경망이 적절한 스케일을 학습하도록 함
- 𝛽 (Shift parameter): 신경망이 특정한 평균을 학습할 수 있도록 정규화된 값을 이동시키는 역할

- 배치 정규화 후 학습 가능한 두 개의 매개변수 𝛾와 𝛽를 도입하여 원래 입력값(Identity function)을 회복시켜줌
- 문제점 2
- 배치 정규화는 미니배치(minibatch)에 의존하는 방식인데, 이 과정에서 사용하는 평균과 분산은 훈련 중 매 미니배치마다 다르게 계산되어 훈련 데이터에 따라 정규화 기준이 계속 바뀜
- 문제점 2의 해결책
- training과 test 과정을 다르게 설정
- training: 각 미니배치에서 평균과 분산을 계산하여 정규화하지만, 동시에 전체 데이터의 평균과 분산을 추적하기 위해 지수 이동 평균(EMA)을 업데이트
- test: 훈련 동안 저장된 스칼라 값인 이동 평균과 이동 분산을 사용하여 정규화하므로 미니배치를 다시 계산할 필요가 없고, 이는 테스트 시 샘플 간 독립성을 보장하는 장점

- training과 test 과정을 다르게 설정
14. Batck Normalization for ConvNets
- 합성곱 신경망에서의 배치 정규화는 배치 공간뿐만 아니라 입력의 두 공간 차원에 대해서도 평균을 구함

- Batck Normalization는 Fully Connected Layer나 Convolutional layer 뒤에 들어가거나, 활성화함수 앞에 위치함
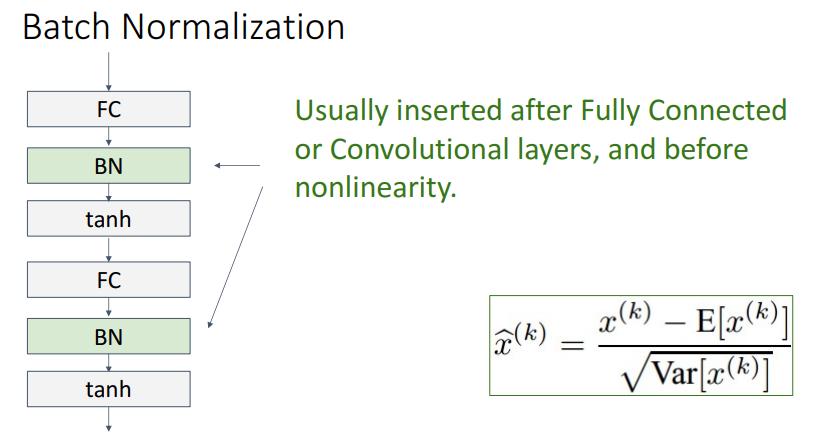
- 장점
- 심층 신경망 학습을 쉽게 할 수 있음
- 배치 정규화는 내부 공변량 변화(Internal Covariate Shift) 를 줄여주어 각 층의 입력 분포가 일정하게 유지되므로, 학습 과정이 더 안정적
- 학습 중에 발산하지 않고 leraning rate를 높일 수 있고, 빠른 수렴 속도를 가짐
- 정규화된 입력을 사용하면 기울기(Gradient)가 적절한 범위를 유지할 수 있어 더 높은 학습률(Learning Rate, LR) 을 사용할 수 있음
- 일반적으로 높은 학습률을 사용할수록 최적점에 빠르게 도달할 수 있음
- 초기화에 덜 민감함, robust함
- BN을 사용하면 입력이 평균 0, 분산 1로 정규화되므로 초기화에 대한 민감도가 줄어듦
- 훈련 중 정규화 역할 수행
- 배치 정규화는 훈련 중 각 미니배치에서 평균과 분산을 계산하는데, 이는 일종의 노이즈 추가 효과를 가져 정규화 역할을 수행할 수 있음
- test 시 오버헤드, 추가연산이 없음, 합성곱 연산과 병합 가능
- 훈련 중에는 미니배치의 평균과 분산을 계산해야 하지만, 테스트 시에는 저장된 이동 평균(Running Mean)과 이동 분산(Running Variance)을 사용하기 때문에 추가 연산 비용이 없음
- 심층 신경망 학습을 쉽게 할 수 있음
- 단점
- 이론적 해석 부족
- 배치 정규화는 실험적으로 매우 효과적이지만,정확히 왜 이렇게 잘 작동하는지에 대한 이론적인 분석은 아직 완전히 밝혀지지 않았음
- 훈련과 테스트에서 동작 방식이 다름
- 훈련 시에 각 미니배치에서 평균과 분산을 계산하여 정규화하고, 테스트 시 훈련 중 계산된 이동 평균과 이동 분산을 사용하여 정규화하는데 이러한 차이로 인해 배치 크기가 달라질 경우 예상치 못한 결과가 나올 수 있음 --> 버그의 흔한 원인!
- 이론적 해석 부족
15. Layer Normalization
- Batch Normalization에서 훈련과 테스트에서 동작 방식이 달라 생기는 문제를 해결하기 위함
- 배치 차원에 대한 평균을 계산하는 대신 피쳐 차원 D에 대한 평균을 계산
- 훈련 및 테스트 시간에 동일한 작업을 진행할 수 있음
- RNN과 Transformer에서 일반적으로 사용

16. Instance Normalization
- 배치 차원에 대한 평균과 피쳐 차원 D에 대한 평균을 계산하는 대신 공간 차원에 대해서만 평균을 계산

17. Comparison of Normalization Layers
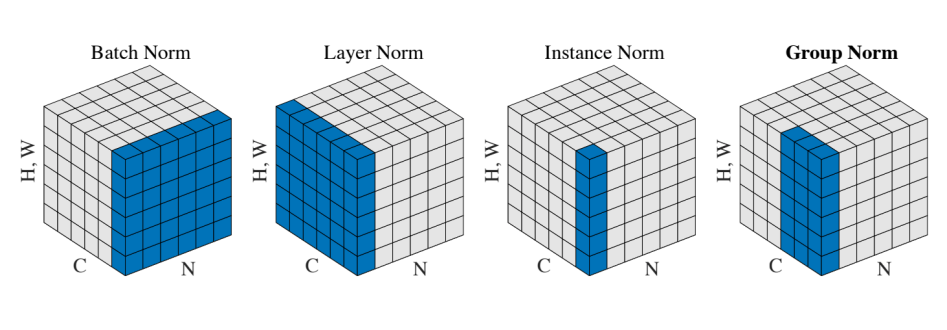
- Batch Norm: 배치 내에서 채널별로 정규화 (같은 채널의 모든 샘플 기준)
- Layer Norm: 하나의 샘플 N에 대해 모든 채널(C)과 공간(H, W)을 한꺼번에 정규화.
- Instance Norm: 한 샘플 N 에 대해 각 채널별로 개별 정규화 (즉, H, W만 고려)
- Group Norm: Instance Norm과 Batch Norm의 절충안으로 채널을 그룹으로 묶어 정규화하므로, 배치 크기에 덜 민감함
