Intro

Binary Search Tree (BST)에 대해 자세히 알아보기 전에 다른 친구들을 좀 알아보자.

Sorted Arrays

정렬된 배열에 대해서 Insert/Delete/Search 연산의 시간을 알아보자.

• Insert/Delete
  얘네는 단순히 처음부터 탐색하며 맞는 자리에서 작업을 실행하면 된다: $O(n)$

• Search
  정렬된 배열에 대해서는 Binary Search를 사용할 수 있다: $O(log(n))$

Linked List

Linked List는 주소를 기반으로 하는 리스트이기 때문에 오히려 단순하다.

• Insert
  그냥 맨 앞에다가 붙이면 그만이다: $O(1)$

• Search/Delete
  next node pointer만 잘 따라가다보면 찾을 수 있다: $O(n)$

But..

$O(log(n))$ 정도까지는 빠르다고 할 수 있는 정도의 시간이다,

하지만 $O(n)$은 생각보다 느리기 때문에, 우리는 모든 연산을 $O(log(n))$에 해낼 수 있는 방법을 찾는 것이다.

Binary Search Tree

BST는 기본적으로 아래의 구조를 따른다.

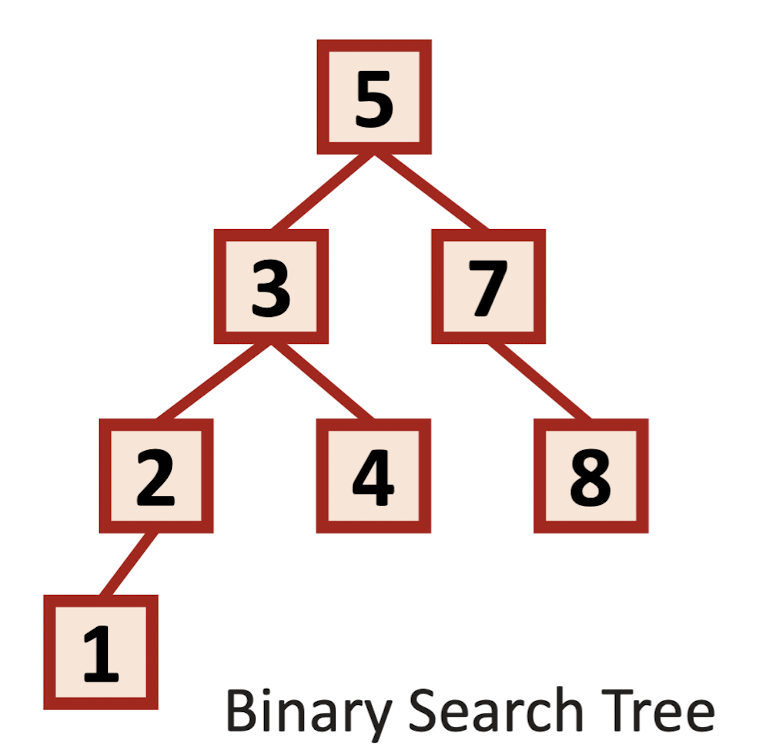
이것만 보고도 BST의 rule을 찾아낼 수 있다면 이제는 정말 프로 출신이다.

root를 기준으로 왼쪽 sub tree는 작은 수, 오른쪽 sub tree는 큰 수들이 존재한다.

물론 root가 아닌 다른 노드들에 대해서도 다 성립한다.

Search

그럼 BST에서 특정 수를 찾는 방법을 알아보자.

예를 들어 4를 찾고 싶다면?

일단 root에서 시작한다.

4는 반드시 5보다 작은 수이다.

그러므로 왼쪽 sub tree로 이동한다.

그 sub tree의 root는 3이며, 4는 3보다 크므로 반드시 오른쪽 sub tree에 있을 것이다.

그렇게 이동을 해보면 4가 있는 것을 확인할 수 있다.

if...

만약 tree에 존재하지 않는 수를 찾으려 하면 어떻게 될까?

없다고 반환할 수도 있겠지만, 친절한 BST는 찾는 경로에서 가장 마지막에 들렀던 노드를 반환해준다.

4.5를 찾으려 했다면 4를 반환해준다는 것이다.

Run Time

BST에서 Search를 하는 경우는 방금 느꼈겠지만 아무리 느려도 tree의 height보다는 오래 걸릴 수가 없다.

Insert

Search를 잘 이해했다면 Insert는 뭐 아무것도 아니다.

일단 우리가 Insert하고 싶은 것을 key라고 하자.

그렇다면 가장 먼저 할 일은 Search(key)를 하는 것이다.

아니 왜 Insert를 하는데 Search를 하나요??

아직도 아마추어다.

아까 뭐라했지? 없는 걸 찾으려고 하면 가장 가까운 값을 반환한다.

그렇다면 key가 반환값보다 작으면 왼쪽, 크면 오른쪽에 넣으면 된다.

얼마나 단순한가.

Run Time

그냥 Search만큼 시간이 걸린다.

어차피 노드를 붙이는 일은 상수 시간에 처리가 되니까.

Delete

Delete는 살짝 어렵다.

일단 지울 것을 찾기 위해 Search를 한다는 사실까지는 변함이 없다.

그리고 여기서 Case가 3개로 나뉜다.

Case 1

delete 하려는 노드가 leaf 노드일 때는 그냥 깔끔하게 그 친구만 지우면 된다.

Case 2

delete 하려는 노드가 자식 노드를 1개 가지고 있을 때는 지우고, 자식 노드를 부모 노드 아래에 붙이면 된다.

Case 3

이 케이스가 가장 헷갈린다.

delete 하려는 노드가 자식 노드를 2개 가지고 있을 때이다.

이런 경우는 지우고 그 자리를 트리 내에서 바로 다음으로 큰 수로 채우면 된다.

이제 여기서 체크해야 할 것이 있다.

• 그 바로 다음 수가 자식 노드를 2개 갖고 있으면?
  • 이런 경우는 없다. 그 수는 지운 노드의 오른쪽 sub tree에서 가장 작은 수이므로 leaf 노드이거나, 오른쪽으로 뻗는 자식노드만 있을 것이다. 그런 경우는 Case 1과 Case 2에 해당하므로 문제 없이 처리할 수 있다.

Run Time

Delete도 결국 Search를 기반으로 하는 로직이므로 height보다 오레 걸리지는 않는다.

Run Time

이러면 3개의 연산 모두 실행 시간이 $O(log(n))$임이 증명된다!

But..

근데 이런 경우가 있을 수도 있다.

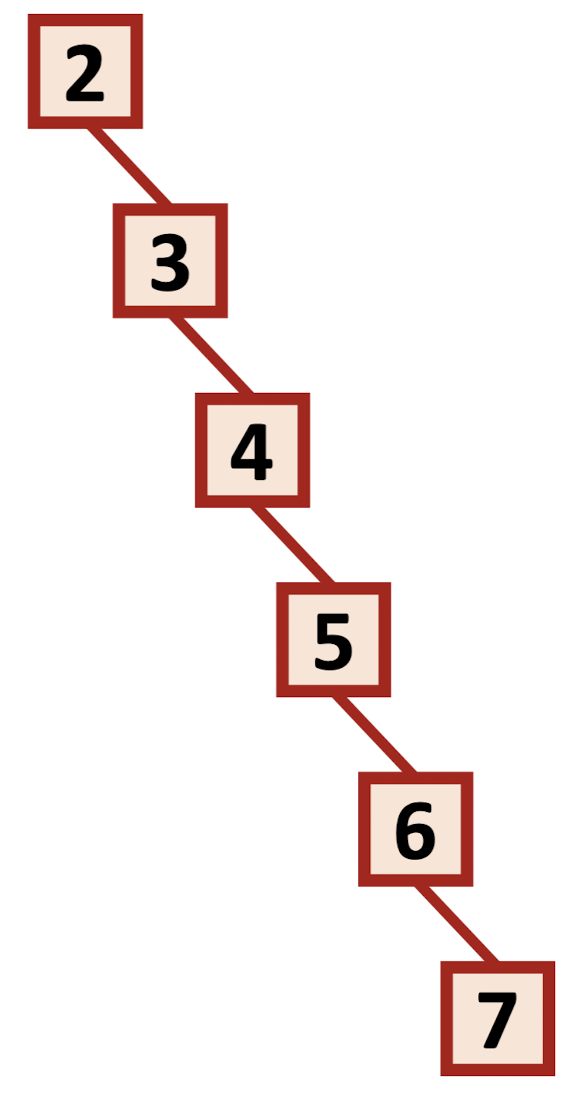
이게 BST가 맞냐고? 맞다.

왼쪽 sub tree가 없을 뿐이다.

이런 경우는 height와 input size가 같기 때문에 Search에 $O(n)$ 시간이 걸린다.

BST의 worst case라고 볼 수 있겠다.

그럼 어떻게 해결해야하나...

Rotation

BST를 특정 노드를 기준으로 돌리면 된다.

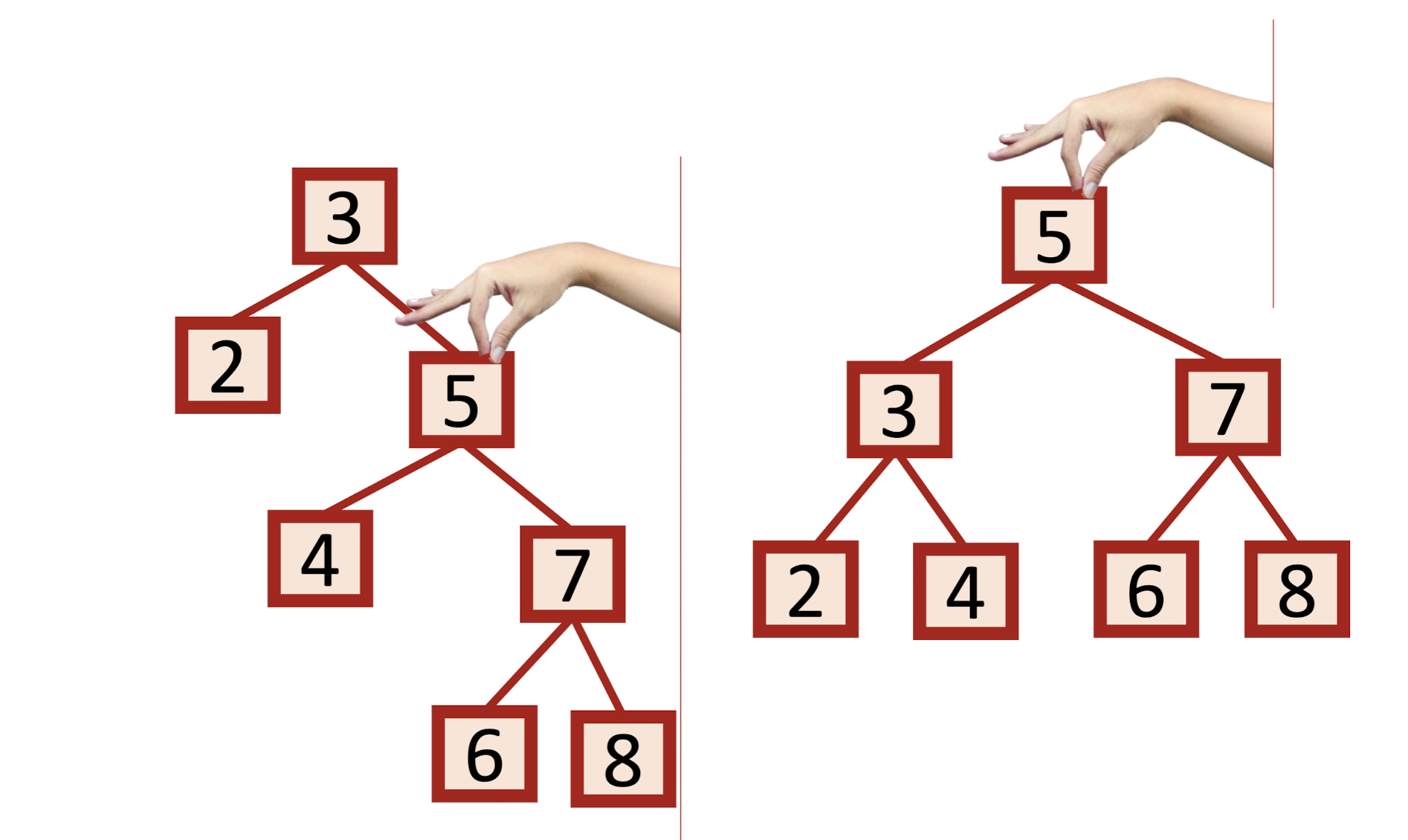
마치 실로 연결 되어 있는 공들을 중심을 잡고 그대로 축 늘어트린다고 생각하면 된다.

나름 일리있어 보인다.

근데 문제가 있다.

좀 불균형하게 생겼네? 싶으면 돌리면 되지만, 그 "불균형하다"에 대한 정의가 참 어렵다.

Red-Black Tree

그래서 나온 것이 Red-Black Tree이다.

Rule

Red-Black Tree에는 5가지 규칙이 있다.

1. 모든 노드는 Red or Black
2. Root 노드는 반드시 Black
3. NIL 노드는 반드시 Black
4. Red 노드 밑에는 반드시 Black
5. 특정 노드 x에서 leaf까지 가는 모든 경로는 Black 노드의 수가 같다.

아래의 예시들을 보자.

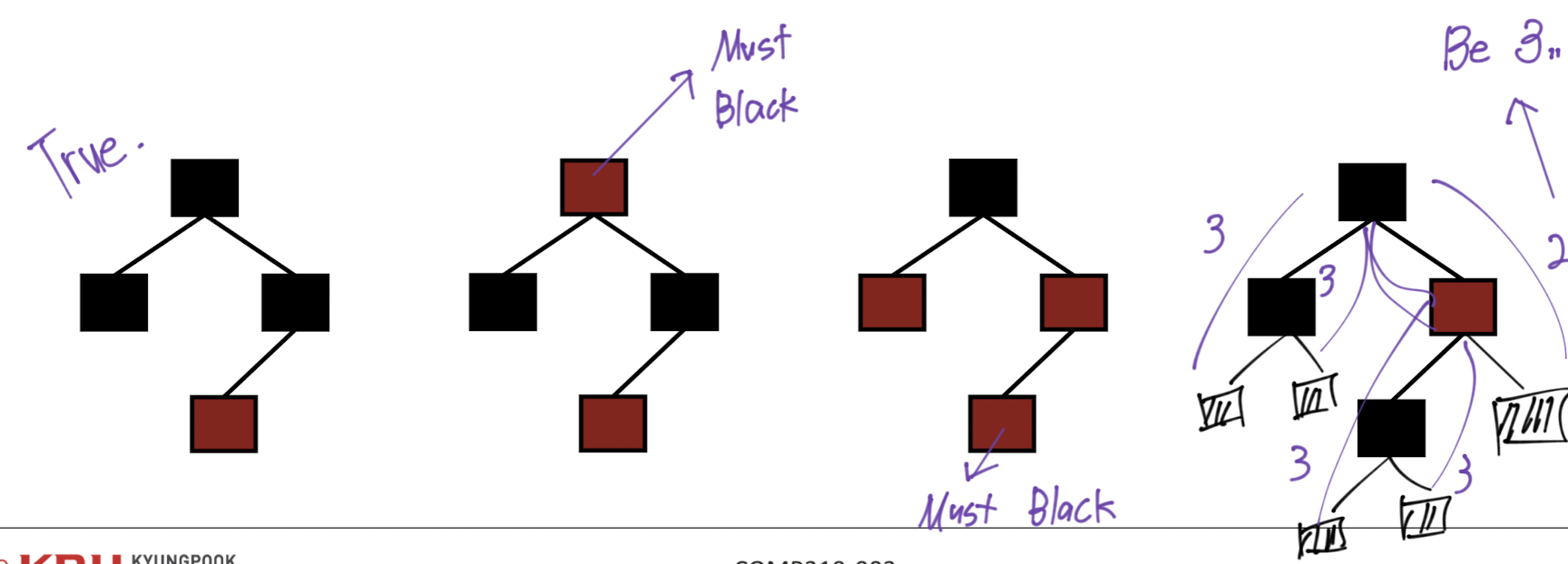
첫번째는 Red-Black Tree이다.

두번째는 2번에 어긋나고, 세번째는 4번에 어긋난다.

네번째 경우가 좀 중요하다.
5번에 어긋나는 경우인데, root노드를 기준으로 총 5개의 NIL이 있다.
하지만 가장 오른쪽 NIL에 가는 경로에는 Black 노드가 2개 밖에 포함되지 않는다.

Why?

왜 이런 식으로 규칙을 정한 것일까?

하나 비유를 들어보자.

1. 트리를 하나의 도로라고 했을 때, Black 노드는 검문소, Red 노드는 경로가 너무 혼잡해지지 않도록 갈림길을 만들어주는 공간이다.
2. 도로의 입구는 중요하니까 반드시 검문소를 하나 설치한다.
3. 도로의 끝도 중요하니 반드시 검문소를 설치하자.
4. 한 번 갈림길이 만들어지고 나면 또 다시 검문을 시행한다.
5. 하지만 특정 경로에만 검문소가 많다면 그 경로만 통행 시간이 오래 걸릴 것이므로, 경로마다 같은 수의 검문소를 설치해준다.

이해가 좀 될 지 모르겠다.

처음 이 비유를 봤을 때 뭔가 모든 것들이 깔끔히 정리되는 느낌이었다.

그래서 결국 이론적으로 설명하자면, Black 노드는 밸런스를 잡아주고, Red 노드는 혼잡하지 않게 해주는 역할이다.

Prove

Red-Black Tree가 항상 $O(log(n))$ 시간을 보장한다는 것을 증명해보자.

$b(x)$를 특정 노드 x에서 NIL까지에서 가능 경로에 있는 Black 노드의 수라고 하자.

다만 여기서 x가 Red일 수도 있으므로 x는 개수에서 제외한다.

그럼 이런 주장을 할 수 있다.

x 아래에는 NIL 노드를 제외하고 최소한 $2^{b(x)}-1$ 개의 노드가 있다!

여기서 최소라는 것은 Red 노드를 사용하지 않고 오로지 Black으로만 채우면 저 개수가 된다.

root를 기준으로 하는 수식으로 나타내면 $n \geq 2^{b(root)}-1$ 이 되고,
black 다음에 무조건 red가 오는 경우를 생각하면 $b(root) \geq height/2$ 이므로,
결국 $n \geq 2^{height/2} -1$ 이라는 식이 나온다.

이를 height에 대한 식으로 정리하면, $height \leq 2log(n+1)$ 이 된다.

최대 heght가 $2log(n+1)$ 이므로, 이것이 worst case이고, $O(log(n))$ 이라는 결론이 나온다!

Insert/Delete

Insert와 Delete도 $O(log(n))$의 시간을 보장한다.

Delete는 이번엔 넘어가도록 하고, Insert만 살짝 맛만 보자.

일단 기본적인 rule은 들어가는 node의 색은 초기엔 반드시 red로 들어간다.

이유는 간단하다.

Black 넣으면 매우 매우 당연하게도 Red-Black Tree의 5번 조건에서 벗어나게 된다.

Case 1

이렇게 생겨 먹은 놈(죄다 까만)은 단순하다.

그냥 Red node를 집어 넣으면 Red-Black Tree의 특성을 유지하며 Insert가 가능하다.

Case 2

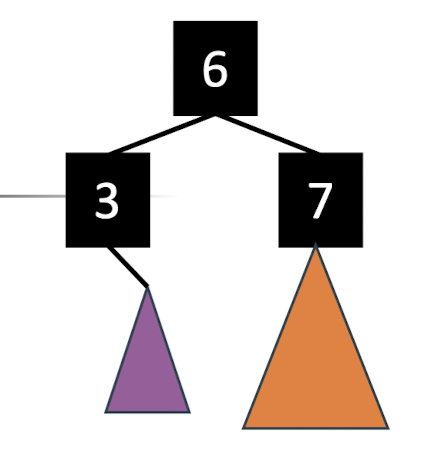
이제 Insert할 노드의 부모 노드가 Red인 경우들이 문제이다.

이럴 때는 삼촌 노드를 슬쩍 쳐다본다.

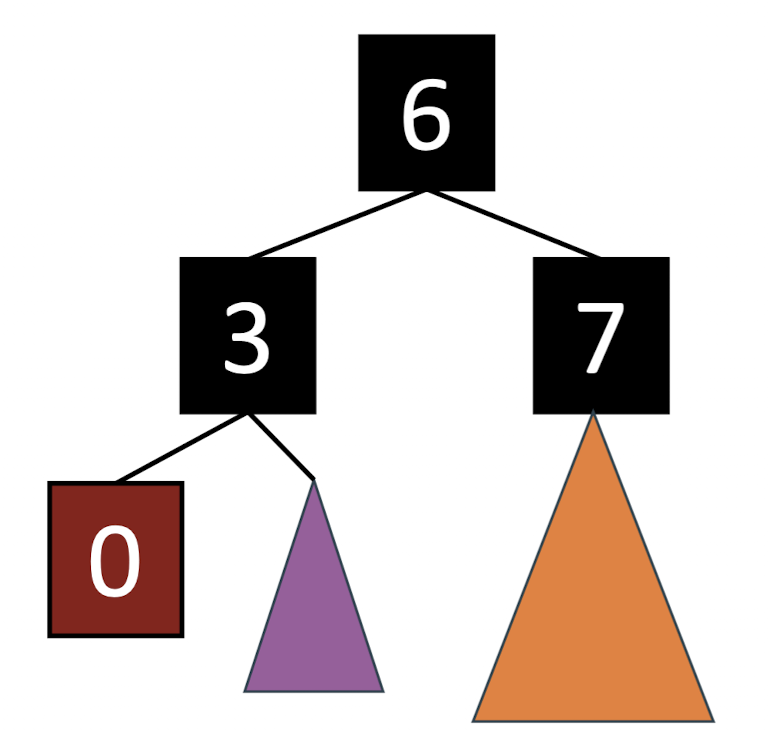
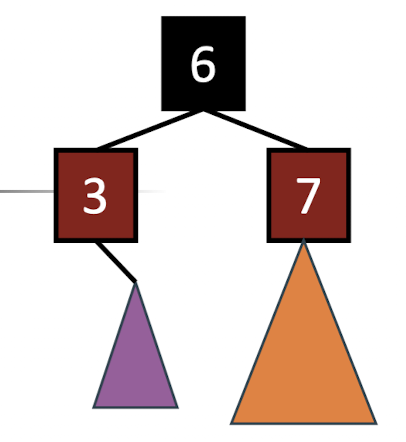
만약 삼촌 노드도 red라면 (조부모 노드 색(반드시 Black)) <-> (부모 노드, 삼촌 노드 색) 를 진행하면 된다.

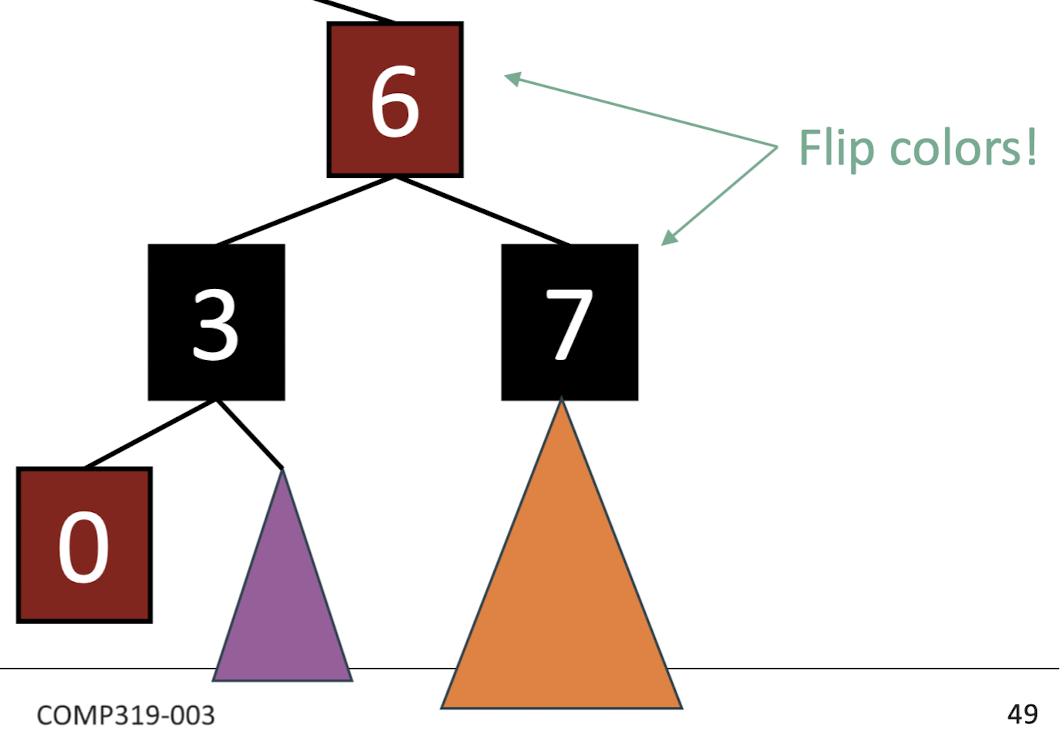
근데 문제가 발생할 수 있다. 조부모 노드의 부모 노드가 red라면,,?

이거 한 번 더 하면 된다.

어디까지 갈 지는 모르겠으나 root 노드는 반드시 black일 것이기 때문에 언젠간 균형이 맞춰질 것이다.

Case 3

마지막 경우는 부모가 red인데, 삼촌이 black인 경우이다.

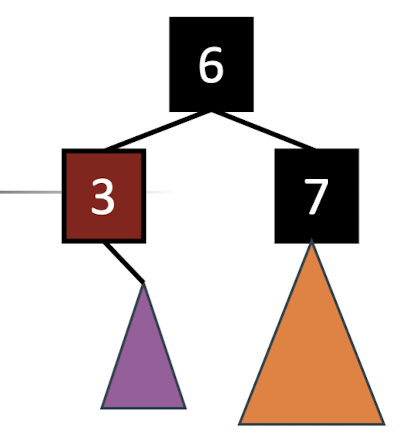
이런 경우 역시 일단 red를 갖다 붙이고, 부모 노드를 최상단으로 들어준다.

Rotation하라는 뜻이다.

조부모와 부모가 바뀌고 나와 동급이 되는 역전 세계이지만 어쩔 수 없다.

Rotation을 진행한 후에는 기존의 부모 노드와 조부모 노드의 색만 바꿔주면 끝이다.

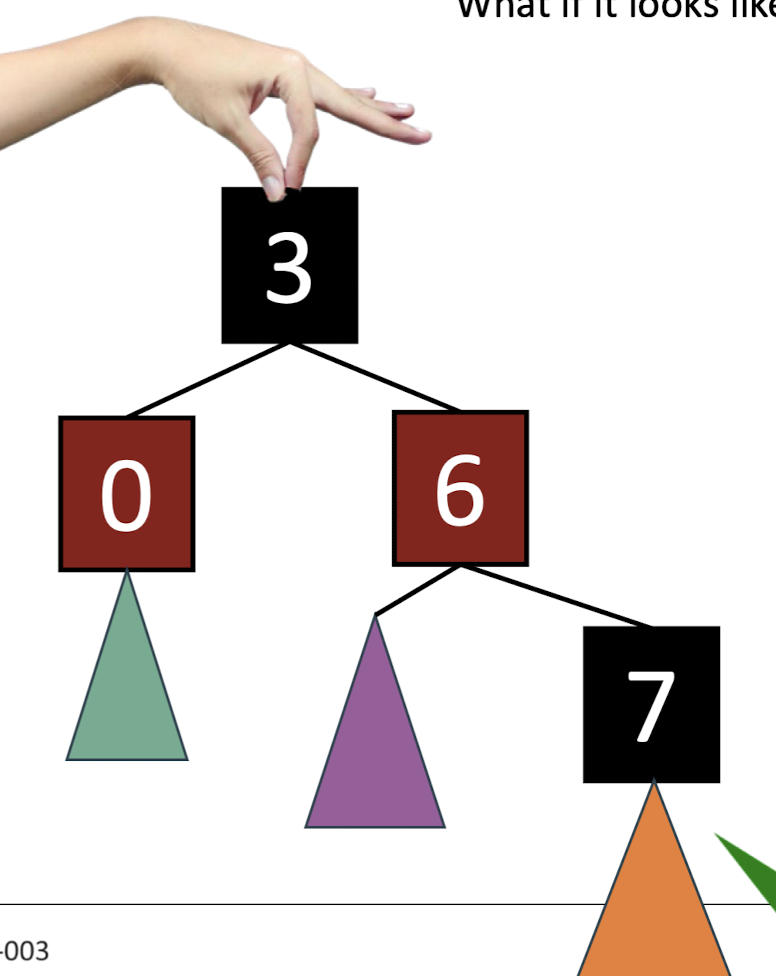
참 쉽죠?

Conclusion

이렇게 BST와 Red-Black Tree에 대해 알아보았다.

어려울 수 있겠지만, 한 번만 이해하면 괜찮은 듯 하다.

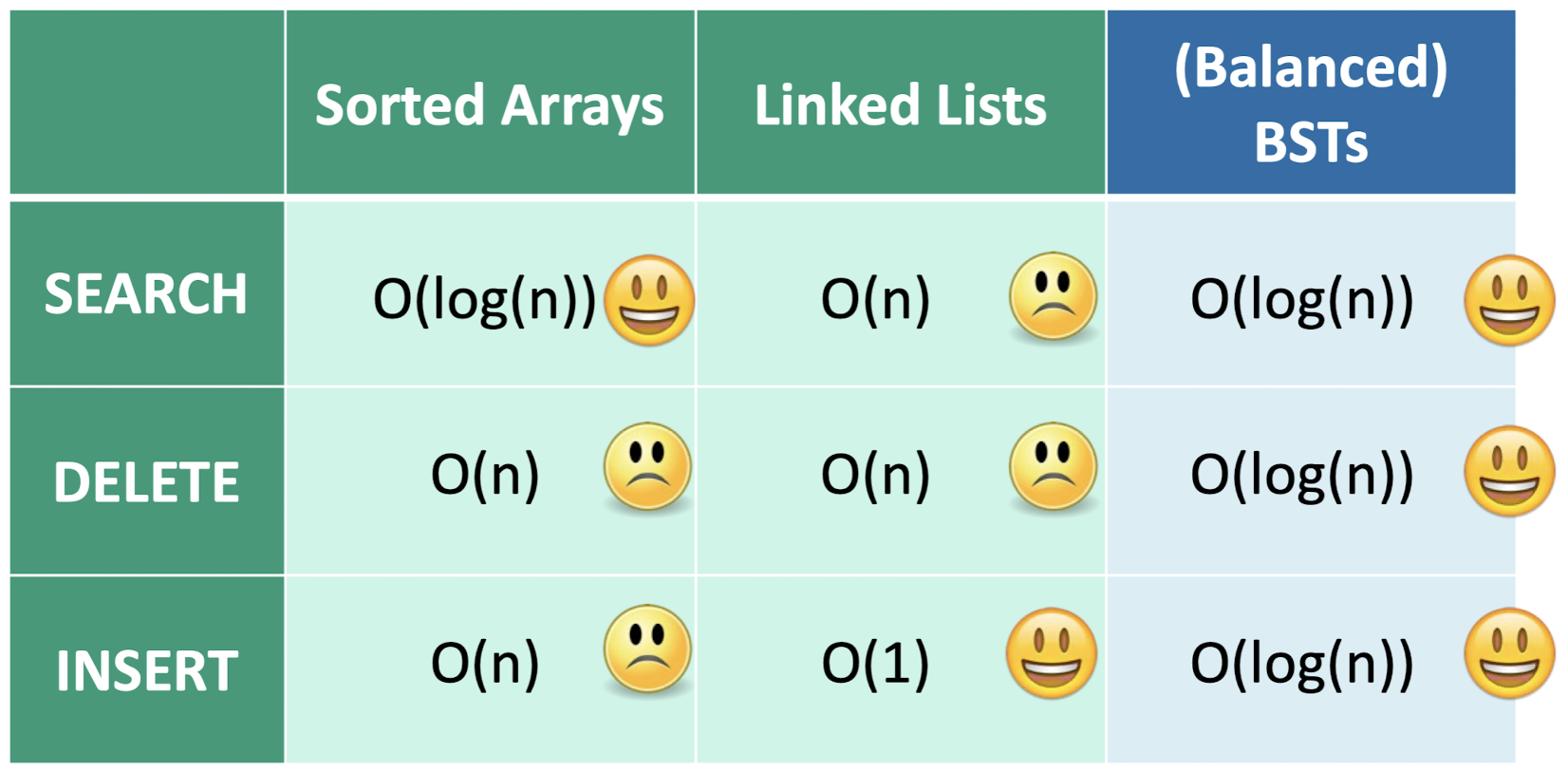
요고를 잘 기억하자~~