Sorting

앞선 글들에서 많은 종류의 Sorting 문제들을 보았다.

하지만 그 어떤 것도 $\Theta (nlogn)$ 보다는 빠를 수 없었다.

그렇다면 정렬은 절대 저것보다 빠를 수 없는 것일까?

일단 정답만 말하자면 꼭 그런건 아니다.

특정한 조건 에서는 $O(n)$ 시간에 정렬을 할 수 있다.

하지만 우리가 지금까지 배운 정렬 알고리즘들은 한 가지 특징이 있다.

바로 두 수를 비교한다는 것이다.

Comparision-Based Sorting

비교 기반의 정렬 알고리즘은 $\Omega(nlogn)$임을 증명해보자.

이는 간단하게 Decision Tree로 증명할 수 있다.

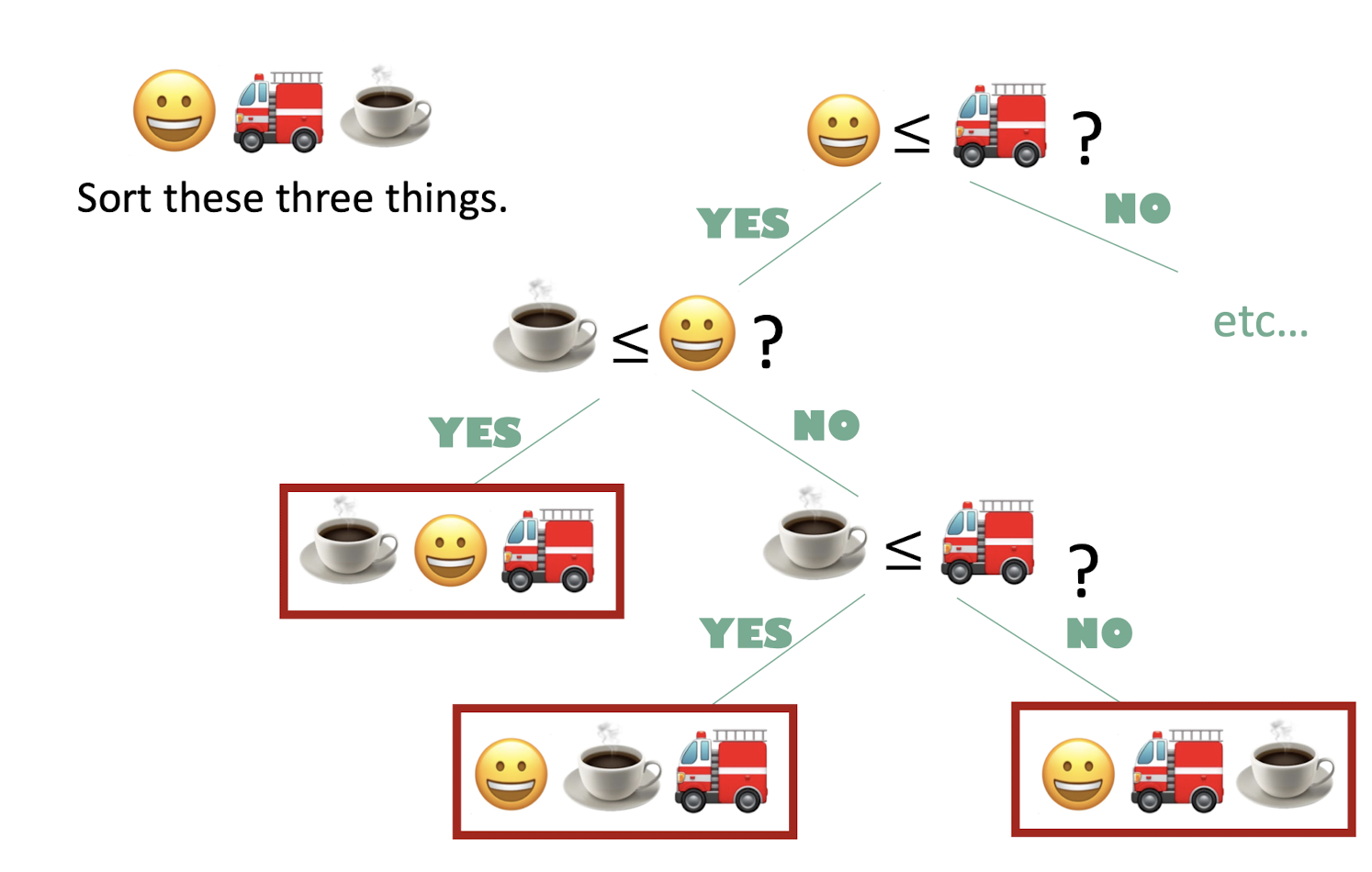
이렇게 3개를 정렬하는 경우 하나하나 비교하며 모든 경우의 수를 찾아본다고 했을 때, 이진트리가 만들어진다.

이진트리에서 원하는 정렬이 된 경우는 leaf node에 있을 것이다. leaf node의 갯수는 $n!$ 개일 것이다. (

이 때 이진트리 중 가장 높이가 낮은 이진트리는 완전이진트리이며, 이 경우 높이는 $log(n!)$, 즉 최단 거리가 $log(n!)$이라는 것이다.

Stirling's formula에 의해 $n!=(n/e)^n$ 으로 근사되며,

$log(n!)=nlog(n/e)= \Omega (nlog(n))$이 된다.