Floating Point

살다보면 소수를 표현하게 될 일이 정말 많습니다.

• $\pi$ = 3.141592...
• $e$ = 2.71828...

그렇기 때문에 컴퓨터에서도 당연히 소수를 표현하는 방법은 존재해야합니다.

이번 챕터에서는 이 소수를 표현하는 방법을 알아볼 것 입니다.

Scientific notation

컴퓨터에서 소수를 표현하기 위해서 기본적으로 알아야할 것은 scientific notation 입니다. 한글로는 과학적 표현법이라고도 하는 이 방법은 쉽게 설명하면 그냥 긴 수를 조금 간단하게 만드는 것입니다.

예를 하나 들어보겠습니다.

$0.000001$ 이라는 수가 있을 때, 일일이 소수점이 몇자리인지 세고 하는 거 보단 $1 \times 10^{-6}$ 로 나타내는 것이 좀 더 간단하고 직관적이며 편해보입니다.

바로 이것입니다. 소수점 왼쪽으로는 0을 제외한 단 하나의 정수만을 두고, 소수점 아래로 다 작성한 뒤 10의 거듭제곱으로 나타내는 것입니다.

컴퓨터에서는 2진법을 사용하기 때문에 1만 올 것이며, 마지막엔 2의 거듭제곱으로 나타나게 될 것입니다.

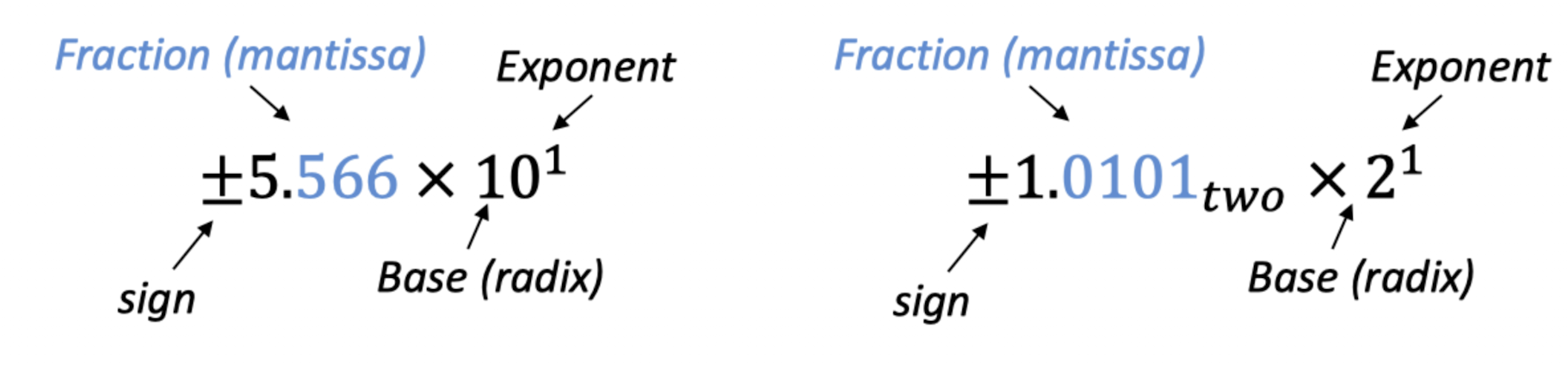
FP number representation

fraction과 exponent는 서로 trade-off relationship을 가집니다. fraction에 bit를 더 할당하면 더 정밀한 표현이 가능하고, exponent에 bit를 더 할당하면 더 큰(작은) 수를 표현할 수 있게 됩니다.

현재 컴퓨터에서 사용되는 FP 표현을 위한 bit 할당은 아래와 같이 되어있습니다.

exponent에 8bit가 할당되어 있기 때문에 -128부터 127까지를 표현할 수 있으며, 10진수 기준 $2 \times 10^{-38} \sim 2 \times 10^{38}$ 만큼의 범위를 가집니다.

64bit인 경우 위와 같은 bit 할당을 하며, 더 정밀하고 더 큰 수를 표현할 수 있게 됩니다.

Bias notation

이렇게 끝내면 될 것 같지만 작은 문제가 하나있습니다.

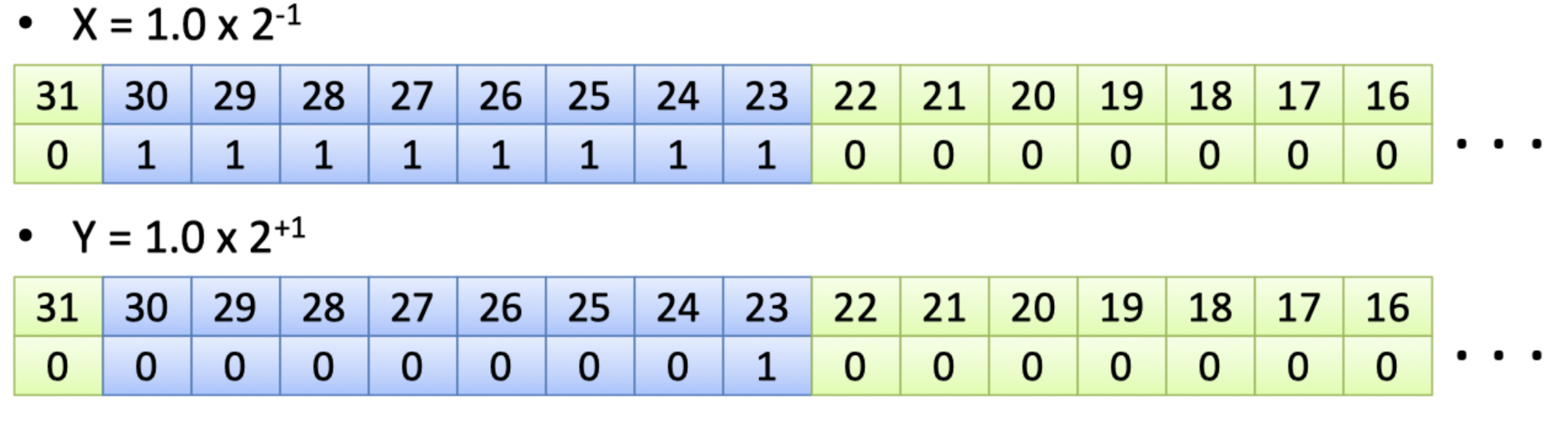
위의 그림을 보고 X와 Y를 비교하면 사람의 눈엔 -1과 1을 보고 당연하게도 X가 더 작다고 말할 것입니다. 하지만 컴퓨터는 그렇지 않습니다.

컴퓨터가 가장 먼저 다르게 인식되는 부분은 index 30의 1과 0일 것이며, 이것만 보면 X가 더 크다고 판단하게 됩니다. 그래서 정확한 대소비교를 하기 위해서는 끝까지 다 읽고 비교하는 과정을 거쳐야하는데, 이는 꽤 시간을 많이 사용합니다.

이를 개선하기 위해 bias notation을 사용합니다.

00000000을 가장 작은 수로, 11111111을 가장 큰 수로 설정합니다.

그리고 실제로 연산을 할 때는 $bias = 2^{k-1}-1$ 를 사용하여 32bit인 경우 127만큼을 빼고 연산합니다.

최종적으로 flaoting point를 나타내는 식은 아래와 같습니다.

Density of FP Numbers

32bit으로 표현할 수 있는 수의 개수는 $2^{32}$로 정수든 소수든 동일합니다.

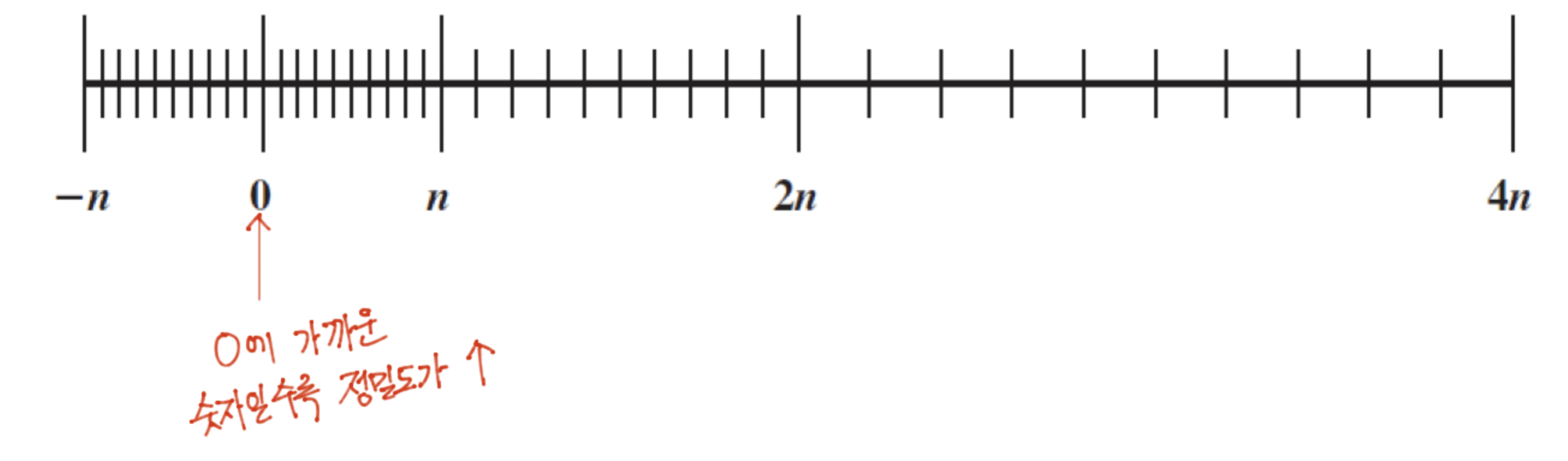
그렇기 때문에 정수는 균일한 간격, 같은 정밀도로 수들을 표현하게 됩니다.

하지만 소수는 fraction과 exponent로 나눠져있고, exponent의 값이 작아질수록 좀 더 정밀한 값을 나타내기 때문에 0에 가까운 곳일 수록 수가 더 촘촘히 배치되어있습니다.

Floating Point Addition

마지막으로 FP의 덧셈에 대해서 알아보겠습니다. 과정은 간단히 4개로 나눌 수 있습니다.

1. Align
2. Add significands
3. Normalize, check over/underflow
4. Round

예시를 하나 들어보겠습니다. 일단 기본적으로 유효 숫자는 4자리까지만 저장할 수 있다고 가정하겠습니다.

$9.999_{10} \times 10^{1} + 1.610_{10} \times 10^{-1}$
$\rightarrow 9.999 \times 10^{1} + 0.016 \times 10^{-1}$ (소수점 정렬)
$\rightarrow 9.999 + 0.016 = 10.015 \times 10^{1}$ (유효숫자 더하기)
$\rightarrow 1.0015 \times 10^{2}$ (정규화)
$\rightarrow 1.002 \times 10^{2}$ (반올림)

위와 같은 과정을 거치면 FP 덧셈이 완료됩니다. 2진수로 계산하는 예시까지 확인 후 마무리하겠습니다.

$0.5_{10} + (-0.4375)_{10}$

• $0.5_{10} = 0.1_{2} = 0.1 \times2^{0} = 1.000 \times 2^{-1}$
• $0.4374_{10} = 7/16 = 7/2^{4} = 111 \times 2^{-4} = 1.110 \times 2^{-2}$

$\rightarrow 1.000 \times 2^{-1} - 1.110 \times 2^{-2} = 1.000 \times 2^{-1} - 0.111 \times 2^{-1}$ (소수점 정렬)

$\rightarrow 1.000\times 2^{-1} - 0.111\times 2^{-1} = 0.001\times 2^{-1}$ (유효숫자 더하기)

$\rightarrow 1.0 \times 2^{-4}$ (정규화, 반올림 생략)