Minimum & Maximum

제목은 선형시간선택이지만, 간단하게 하나 짚고 넘어가자.

어떤 리스트에서 최솟값이나 최댓값을 찾으려면 어떻게 해야할까?

어렵게 생각할 일은 아니다.

순서대로 앞에서부터 비교하면서 교체해주면 된다.

참 쉽죠?

Selection

자 그럼 특정 위치에 있는 원소를 찾아보자.

여기서 말하는 위치는 물리적 위치는 아니고, k번째로 작은 수 를 의미한다.

예를 들어 [3, 4, 6, 7, 9, 1]과 같은 리스트가 있을 때, 3번째로 작은 수는 4이다.

Naive

간단하게 생각해보면 어렵지 않다.

리스트를 정렬하고, k번째를 가리키면 된다.

하지만 우리가 지금까지 배운 정렬 중 가장 빠른 건 merge sort이고, $\Theta(nlogn)$ 시간이 걸린다.

그 말은 select에 걸리는 시간도 최소 저만큼은 걸린다는거다.

Linear-Time Selection

하지만 제목에서도 알 수 있듯이 우리는 저런 느려터진 알고리즘을 원하는 것이 아니다.

선형 시간, 즉 $\Theta(n)$ 시간의 알고리즘을 원한다.

Idea

그럼 그 아이디어는 어디서 나오냐?

앞서 배웠던 Quick Sort에서 고안한다.

1. 단 pivot을 정하고
2. 제 partitioning을 한다.

그 후엔 pivot 기준 왼쪽에는 더 작은 수, 오른쪽에는 더 큰 수만 남는다.

여기서 살짝 생각을 바꿔보자.

난 pivot의 index를 알고, 원하는 수가 정렬 됐을 때의 index인 k도 안다.

대충 느낌오죠?

1. k가 pivot의 index보다 작으면 Left에 있을 것이고,
2. k가 pivot의 index보다 크다면 Right에 있을 것이다.

이렇게 찾다가 pivot의 index == k가 되는 그 위치가 바로 우리가 원하는 그 수가 있는 자리다.

근데 Quick Sort랑 같은 아이디어라면 $\Theta(nlogn)$ 아니냐고?

하나 다른 것이있다.

Quick Sort는 정렬을 위해 Left, Right를 둘 다 재귀를 돌지만, 여기서는 하나의 값만 찾으면 그만이기 때문에 없는 쪽은 고려할 필요도 없다.

그래서 슈도 코드를 보면 이런 식이다.

Prove

자 다시 돌아온 증명 시간이다.

아 그럼 이번에도 Partitioning을 증명하면 되겠네!

라고 생각한 당신은 너무 아마추어다.

이미 증명된 걸 왜 또 증명하고 앉아있겠냐.

저기 3개의 Case들에 대해서 각각 증명하도록 하자.

Inductive Hypthesis

귀납 가설부터 세워보자.

크기 𝑛인 배열 𝐴와 정수 𝑘 ∈ {1, . . . , 𝑛}에 대해 실행될 때, SELECT는 𝐴의 𝑘번째로 작은 요소를 반환한다.

Base Case

$n=1$ 일 때가 Base Case가 되겠다.

이 경우엔 반드시 $k=1$ 이고, 또한 반드시 $A[1]$을 반환하므로 항상 참이다.

Inductive Step

본격적인 귀납 단계이다.

𝑖 ≥ 2라고 가정하고, 1 ≤ 𝑛 < 𝑖인 모든 𝑛에 대해 귀납 가설이 성립한다고 가정하자.
우리의 목표는 𝑛 = 𝑖에 대해서도 성립함을 보이는 것이다.
1 ≤ 𝑘 ≤ 𝑖라고 가정하고, 𝐴가 길이 𝑖인 배열이라고 하자. 𝐿과 𝑅를 피벗 𝑝의 왼쪽과 오른쪽의 서브리스트라고 하자.
그러면 𝑝에 따라 세 가지 경우를 고려해야 한다.

이제 3가지 case에 대해 나눠서 생각해보자.

• Case1. $|L| = k-1$

  • 여기서 $|L|$은 왼쪽 서브리스트의 길이이다
    이게 $k-1$이라는 것은 $p=k$라는 의미이기 때문에 $A[p]$가 우리가 찾던 $k$번째로 작은 수이다.

• Case2. $|L| > k-1$

  • 왼쪽 서브리스트의 길이가 $k-1$보다 길다는 것은 반드시 $L$ 안에 우리가 원하는 $k$번째로 작은 수가 존재한다.
  • 또한 이는 $L$의 $k$번째 작은 요소가 $A$의 $k$번째 작은 요소와 같다는 것을 의미한다.
  • 위의 귀납 가설을 이용하면, $n=|L|$ 일 때, $|L|<i$ 이므로 성립한다.
  • 마지막으로, $1 ≤ 𝑘 ≤ |𝐿|$이므로, 귀납 가설에 따르면 SELECT(L, k)는 $𝐿$의 $𝑘$번째로 작은 요소를 반환한다.

• Case3. $|L| < k-1$

  • 왼쪽 서브리스트의 길이가 $k-1$보다 작다는 것은 반드시 $R$ 안에 우리가 원하는 $k$번째로 작은 수가 존재한다.
  • 또한 이는 $R$의 $k$번째 작은 요소가 $A$의 $k-|L|-1$번째 작은 요소와 같다는 것을 의미한다.
  • 위의 귀납 가설을 이용하면, $n=|R|$ 일 때, $|R|<i$ 이므로 성립한다.
  • 마지막으로, $1 ≤ 𝑘 - |L| - 1 ≤ |R|$이므로, 귀납 가설에 따르면 SELECT(R, k-|L|-1)는 $R$의 $k-|L|-1$번째로 작은 요소를 반환한다.

Conclusion

• 귀납에 따르면 가설은 모든 $n \geq 1$을 포함한다.

• 그리고 우리는 Select가 $k \in \{1..k\}$인 모든 배열 $|A|$에서 k번째 작은 수를 반환한다고 할 수 있다.

너무나도 복잡한 증명이었다.

Run Time

이제 실행 시간을 구해보자.

점화식은 아래와 같다.

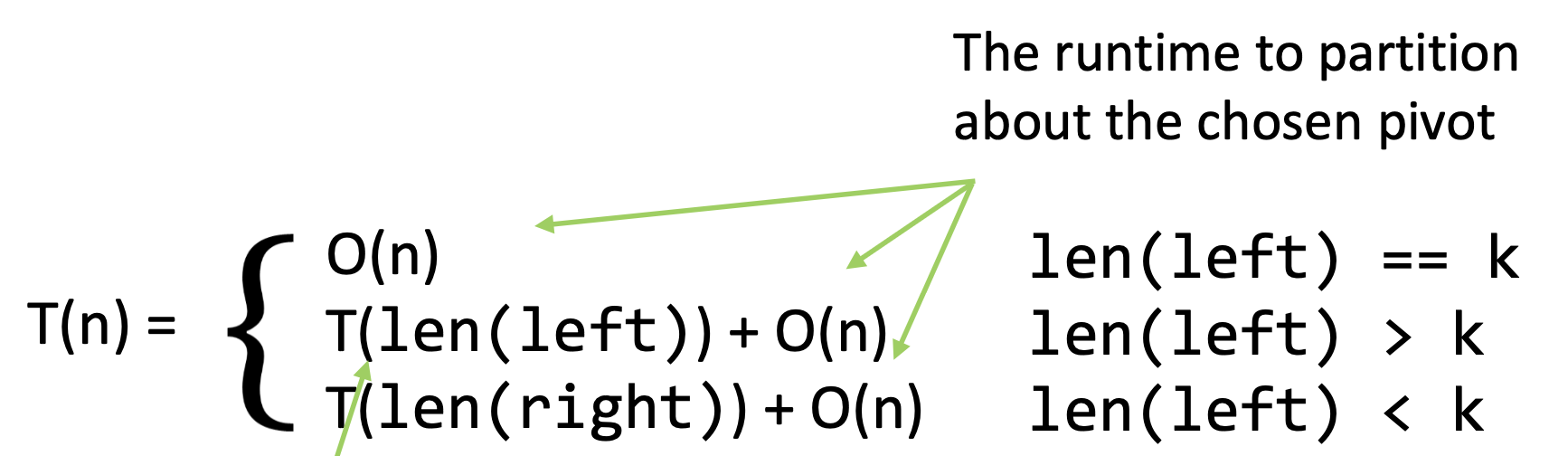
이상적인 경우, pivot이 배열을 절반으로 나눠주기 때문에

$T(n) = T(n/2) + O(n)$ 이다.

Master Method를 적용하면 ?

와! $O(n)$이라는 시간이 나온다.

하지만 우리는 또 또 또! 극단적인 예시를 들어야한다.

pivot이 개같이 선택되면?

늘 그렇듯 $O(n^2)$의 시간이 걸린다.

Select Good Pivot

자 그럼 pivot을 어떻게 선택해야할까...

또 Random을 돌릴 수는 없는 노릇이다.

Quick Sort에서도 어차피 최악은 $O(n^2)$이니까.

가만 생각해보면 대충 중앙값을 pivot으로 선정하면 될 듯 하다.

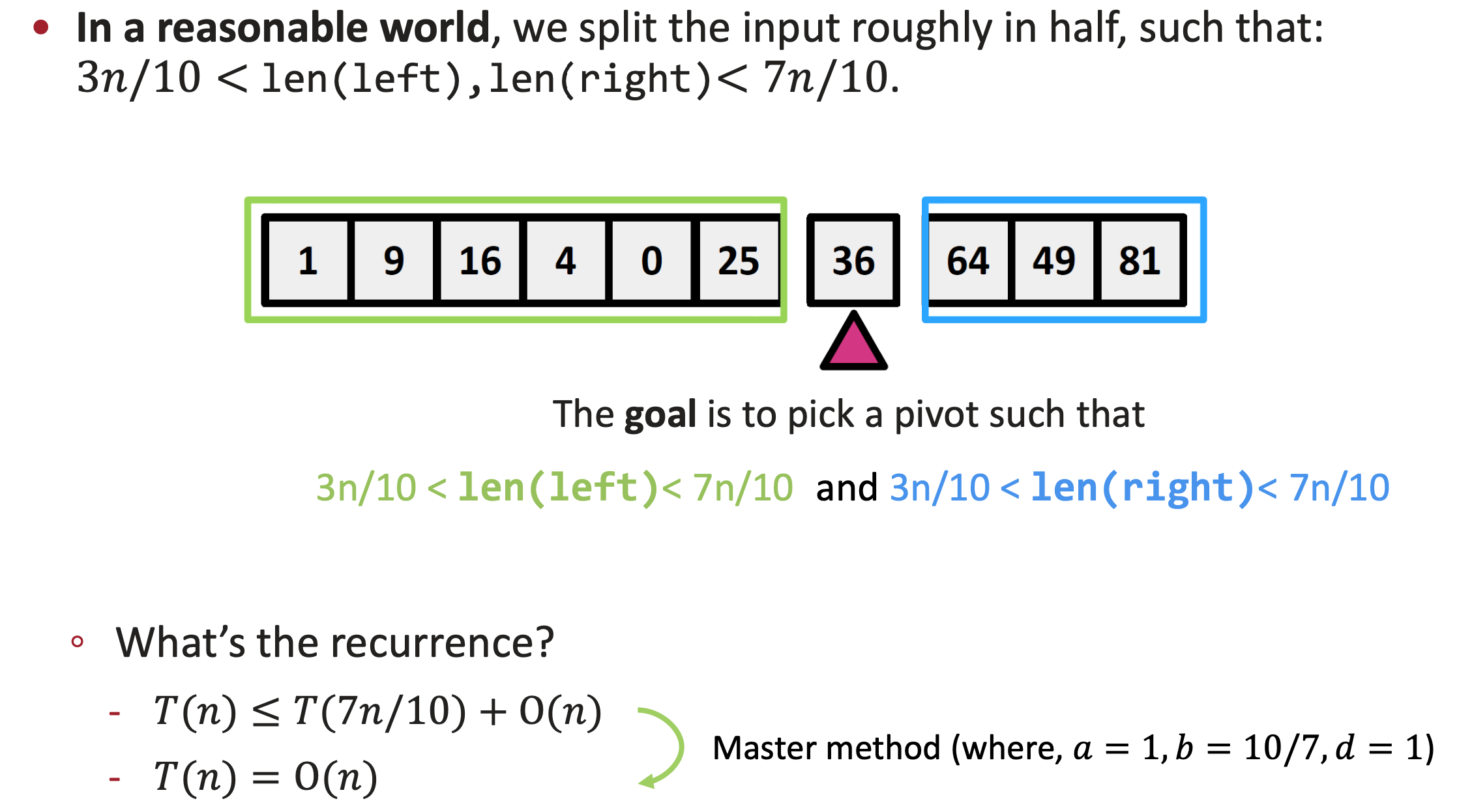
이런 이유에서 꼭 정확히 중앙값일 필요도 없고, 7:3 정도로만 나눠져도 된다.

자 이제 선택을 위한 선택을 해야한다.

대충 중앙값과 비슷한 값을 골라보자.

Median of Medians

우리는 중앙값들의 중앙값을 구해볼거다.

뭔 🐶소린가 싶겠지만 정말이다.

Idea

일단 기본 알고리즘은 DnC이다.

하나의 큰 배열을 길이가 5인 sub array들로 나눈다.

그 sub array들의 median을 구하고, 그 median들의 median을 구한다.

그럼 대~충 전체의 median과 비슷할 것이다.

Prove

근데 이게 전체 배열을 7:3으로 나눠줄만큼이 되냐고?

그것도 증명해야지 어떡해

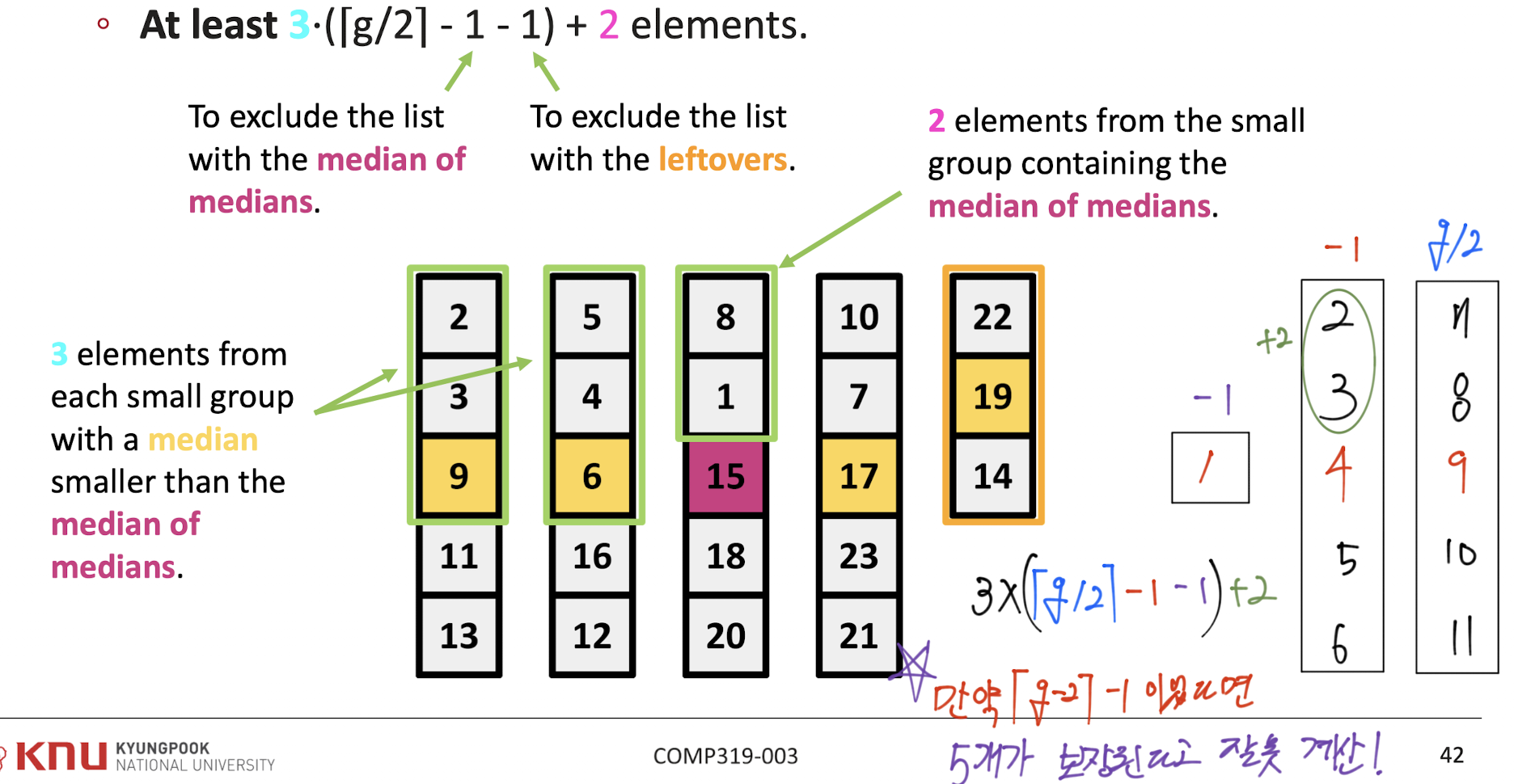
이러한 이유로 최소 개수가 $3(\lceil g/2 \rceil - 1- 1)+2$라는 결론이 난다.

(머릿속에 이유가 다 있다. 진짜임.)

왜 -1을 2번 하냐에 대한 의문은 오른쪽 필기를 보면 된다.

사실 지금 그림에서는 -1을 한 번만 해도 전혀 문제가 없거든요.

아무튼 반드시 median보다 큰 애들의 상한은
$n-1-3(\lceil g/2 \rceil - 1- 1)+2 \leq 7n/10 +3$이고,

median보다 작은 애들의 하한은
$3(\lceil g/2 \rceil - 1- 1)+2 \geq 3n/10-4$ 이다.

아무리 못해도 7:3으로는 쪼개진다는 게 증명이 됐다.

Run Time

마지막으로 시간 계산 한 번 하자.

점화식이 아래와 같아서 Master Method는 못 쓰고, Substitution Method를 써야한다.

$T(n) \leq T(n/5) + T(7n/10) + O(n)$

이건 쓰기 귀찮아서 사진 넣은 거 맞다.

여기서 알아야 할 건 $n \leq 100$ 인 경우는 naive하게 풀어도 크게 시간에 지장이 없기 때문에 base case로 잡은 것이다.

또한 상수 C는 $max(log_2100$, $10d)$ 라는 것도 알고 있으면 좋을 듯 하다.

Conclusion

암튼 이러한 이유로 $O(n)$이라는 선형시간에 Selection을 할 수 있음이 증명 됐다!