Quick Sort

저번까지는 Merge Sort에 치중했다면 이번엔 또 다른 정렬에 대해 알아보자.

물론 이름은 Quick Sort지만 대단히 빠르다거나 그렇지는 않다.

Idea

Quick Sort의 기본 아이디어는 아래와 같다.

1. Pivot(기준 숫자)을 잡는다.
2. Pivot을 기준으로 수들을 나눈다. (Partitioning)
3. 나눠진 두 개의 subarrays에 대해서 같은 작업을 반복한다. (Recursive)

Psuedo Code

슈도 코드를 한 번 보자.

$x = A[r]$이 1번 작업, 그 아래 return까지가 2번, 그리고 Quick Sort를 재귀적으로 도는 것이 3번이다.

Work Flow

첫번째 Partition 작업에 대한 Flow를 보면 이런 형식이다.

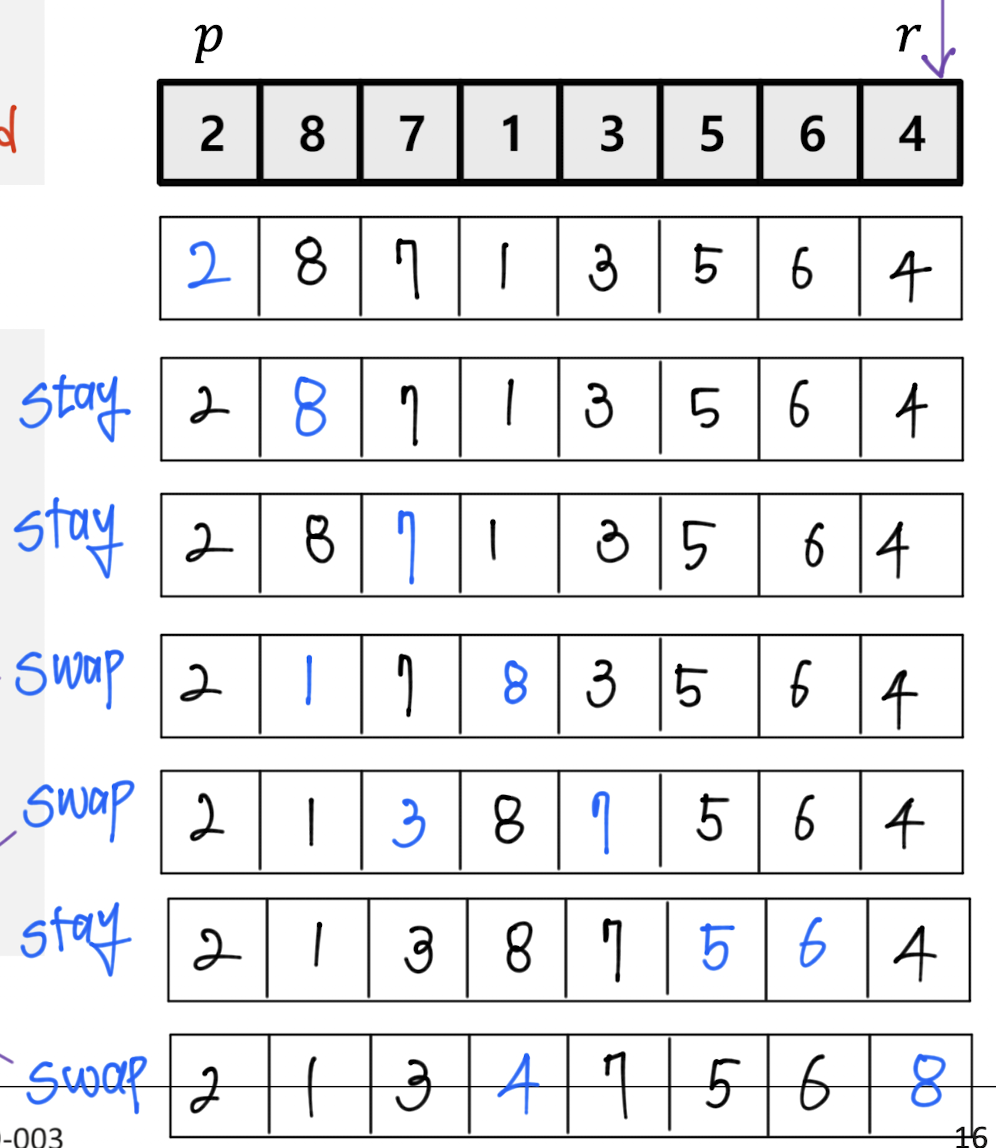
잘 보면 규칙이 있다.

pivot인 4보다 작은 수들은 위치를 바꾸고, 큰 수들은 그 자리에 그대로 있으면 된다.

작은 수들의 위치를 바꾸는 기준은 큰 수 sub-array에서 가장 앞에 있는 수이다.

Prove

대충 이해했을 것이라 생각하고 Correctness 증명 한 번 하자.

이것도 물론 재귀적으로 반복하지만, main logic은 partition이기 때문에 Loop Invariant로 증명을 하면 된다.

Loop Invariant

• $A[p:i] \leq pivot$
• $A[i+1 : j-1] \leq pivot$

초기 조건

• $A[p:i]$ 와 $A[i+1:j-1]$ 모두 빈 array이므로 성립

유지 조건

• Case 1: 지금 가리키고 있는 것 $(A[j])$이 pivot 보다 크다면 $j++$
• Case 2: 지금 가리키고 있는 것 $(A[j])$이 pivot 보다 작다면 $swap(A[i+1], A[j])$ 후 $i++, j++$

종료 조건

• $j=r$일 때 종료
• $A[p:i] \leq pivot$, $A[i+1:r-1] > pitvot$, $A[r] = pivot$

Run Time

놀랍지도 않게 시간도 한 번 분석해보자.

Ideal

이상적인 경우는 어떤 것일까?

pivot이 array를 정확히 반으로 나눠주면 참 좋을 것이다.

그럼 merge sort와 비슷한 성능을 내겠지?

$T(n) = 2T(n/2) + \Theta(n)$ 이니까 Master Method 딱 먹이면
$\Theta(nlogn)$이 된다.

Worst

하지만 우리는 worst case도 생각해야한다.

극단적으로 치우쳐서 pivot이 항상 최댓값으로만 설정된다면?

$T(n) = T(n-1) + T(0) + \Theta(n)$이므로,
수가 1씩 줄어드는 등차수열이라고 생각하면 $\Sigma_{k=1}^nk = n(n-1)/2$ 로 나타낼 수 있다.

그렇다면 결국 n에 대한 2차식이므로 $T(n) = \Theta(n^2)$ 이다.

Average

하지만 평균적인 경우, 아니 오히려 좀 극단적이라고 보이는 경우에도 $\Theta(nlogn)$ 이 성립한다.

아래의 그림을 한 번 보자.

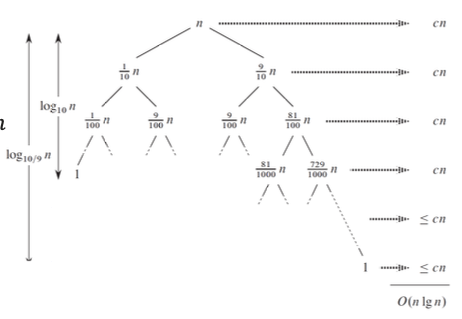
1:9라는 극단적으로 보이는 경우에도 좋은 성능을 자랑한다.

Randomized Quick Sort

자 그럼 저 worst case를 어떻게 극복할 수 있느냐?

pivot을 array의 마지막 원소로 지정하는 것이 아니라 무작위로 선택하는 것이다.

말로만 들으면 당연히 일리있다.

하지만 말을 믿지 않아!!! 증명하자.

Prove

평균적인 run time을 구해보자.

Random Variable

$X_{i, j}$를 pivot에 따른 확률 변수라고 했을 때, i와 j가 비교된다면 1, 아니면 0이라고 하자.

예를 들면 $pivot = 5$일 때, $X_{3,5} = 1$이고, $X_{4,6}=0$이다.

사실 pivot이 아닌 수 2개가 비교 되는 경우는 없다.

i와 j 둘 다 pivot이 아니라면 $X_{i, j}=0$이다.

Expectation

모든 $X_{i, j}$의 조합의 기댓값은 아래와 같다.

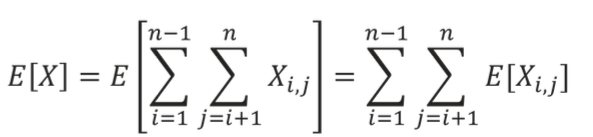
그럼 $E[X_{i,j}]$는 어떻게 구할 수 있을까?

기댓값의 정의에 의해 아래와 같이 나타낼 수 있다.
(기대값 = 사건이 일어날 확률 1 + 일어나지 않을 확률 0)

$E[X_{i,j}] = P\{X_{i,j}\} \times 1 + P\{ \overline {X_{i,j}}\} \times 0$

즉, $E[X_{i,j}] = P\{X_{i,j}\}$

Probability

그렇다면 여기서 $P\{X_{i,j}\}$는 뭘까?

i와 j가 비교 될 확률이다.

0~11까지 있는 array에서 $P\{X_{6,10}\}$ 을 예시로 한 번 들어보자.

pivot이 0~5, 11이라면 6과 10은 한 어느 한 쪽으로 partitioning 되므로 고려할 필요가 없다.

결국 언젠가는 비교되겠지만, 그건 그 때 다시 확률을 구하면 된다.

그럼 우리가 고려할 부분은 pivot이 6~10인 경우이다.

하지만 아까도 말했듯이 i와 j 중에 pivot이 없다면 i와 j는 절대 비교될 일이 없다.

그렇다면 $P\{X_{6,10}\} = {2\over5}$가 된다.

이걸 일반화 시키면 $P\{X_{i,j}\} = E[X_{i,j}] = {2 \over (j-i+1)}$이라는 결론이 나온다.

Conclusion

종합하여 기댓값 식을 정리하면 아래와 같다.

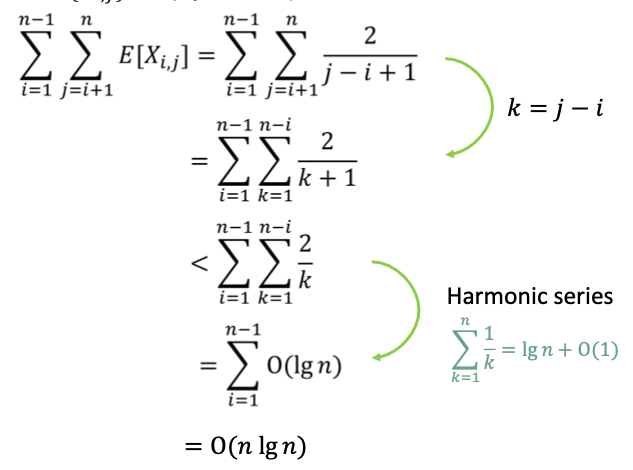
결론적으로 우리는 Randomized Quick Sort를 통해 $O(nlogn)$의 시간을 기대할 수 있다.

But..

Randomize로 worst case를 어느 정도 방지할 수는 있지만, 극악의 확률을 뚫고 여전히 max 값 만 pivot으로 선택되면 $\Theta(n^2)$의 시간이 소요된다.