Binary Search 02

Sources & Credits
https://jovian.ai/learn/data-structures-and-algorithms-in-python/lesson/lesson-1-binary-search-linked-lists-and-complexity

Problem

Alice has some cards with numbers written on them. She arranges the cards in decreasing order, and lays them out face down in a sequence on a table. She challenges Bob to pick out the card containing a given number by turning over as few cards as possible. Write a function to help Bob locate the card.

Cases...
1. The cards are arranged in descending order.
2. Inputs = An array of numbers & the given number.
3. The numbers can be all same numbers.
ex. [2,2,2,2,2,2,2]
4. There could be repeating numbers.
ex. [12,12,12,8,8,8,2,2,1]
5. There could be only a single card/number.
ex. [7]

Lets TEST by Brute Forcing!

def find_card(cards, number):
	current_position = 0
    
    while current_position < len(cards):
    	if cards[current_position] == number:
        	return current_position
        current_position += 1
        
        if current_position == len(cards) - 1:
        	return "Not Found"
            
cards = [24, 19, 13, 10, 7, 5, 2]
number = 10
result = find_card(cards, number)
print(result)

That works but it uses too much resources and time.
Let's try Binary Search!

Let's say we are searching for number 6 in an array and the array is arranged in descending order.

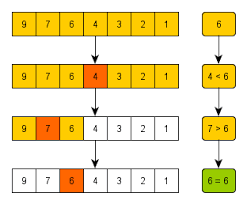
We can start at the middle of the array.
If the number is smaller than the number we are looking for which is 6 in this case, we can ignore the right side of the array since all the numbers on the right side are smaller than 6.
We can only focus on the left part of the array and start again by looking at the middle number which is 7.
7 is bigger than 6 therefore the number to the right would be 6 which we are searching for.

Binary Search is basically dividing the array into half and repeating it until we find the value we are searching for.

Let's write a function to excute the binary search for this problem.

def binary_search(cards, number):
	start, end = 0, len(cards)-1
    
    while start <= end:
    	mid = (start + end) / 2
        current = cards[mid]
        
        if current == number:
        	return mid
        elif current < number:
        	end = mid - 1
        elif current > number:
        	start = mid + 1
    return -1


cards = [24, 19, 13, 10, 7, 5, 2]
number = 5 
result = binary_find(cards, number)
print(result)

Above code might seem right but after doing some edge-case testing found an error.

cards = [8,8,6,6,6,4,4,4,2,2]
number = 6 

Test Result:
FAILED

It's supposed to look for the number 6 but returned an error since the '6' it found wasn't the first '6'.
Because the binary search does not go over the array in a linear order.

When the mid card is equal to the number we are looking for, we need to check whether the mid number is the first one in the array.

def binary_search2(cards, number):
	start, end = 0, len(cards)-1
    
    while start <= end:
    	mid = (start + end) / 2
        current = cards[mid]
	
    	if cards[mid] == number:
    		if mind-1 >= 0 and cards[mid-1] == number:
	        	end = mid - 1
            else:
            	return mid
        elif card[mid] < number:
        	end = mid - 1
        else:
        	start = mid + 1
    return -1

cards = [24, 19, 19, 13, 10, 10, 10, 7, 5, 2]
number = 10
result = binary_find(cards, number)
print(result)

>>> 4

The above function checks whether the number is the first of the array if the mid equals to the number.