Greedy Algorithm 탐욕법

탐욕법은 현재 상황에서 당장 눈 앞에 좋은 것만 고르는 방법을 의미한다. 탐욕법 문제 해결을 위해 단순히 제일 좋아보이는 것을 반복적으로 선택해도 최적의 결과를 구할 수 있는지 분석해야한다.

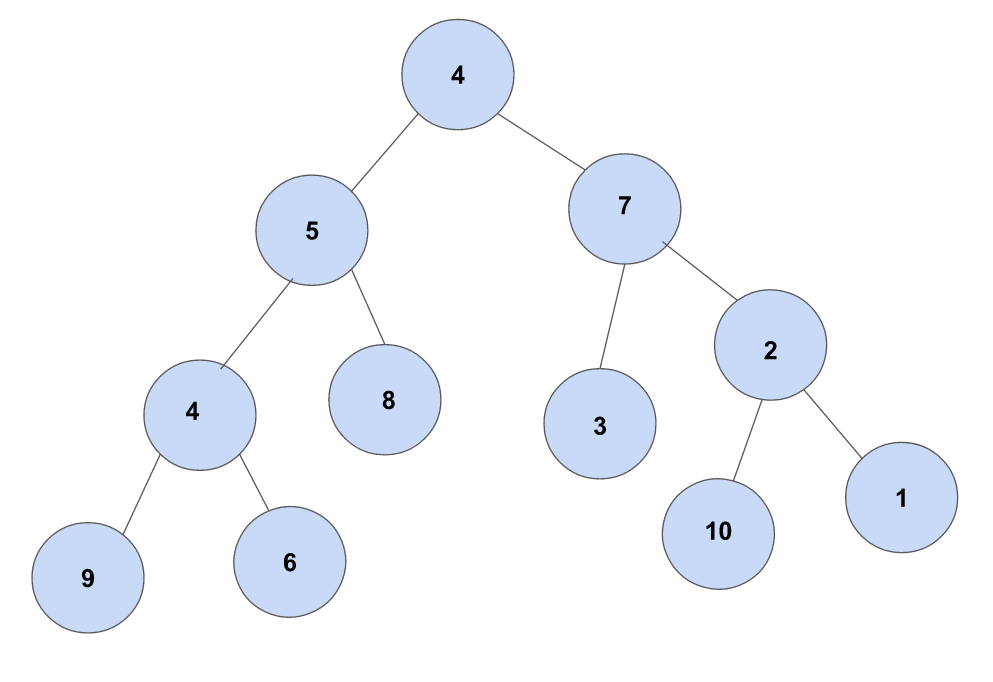
위의 Tree를 기반으로 위에서 부터 아래로 최대 합을 구해야한다고 가정하자. 탑욕법에 따르자면 4로 시작하여 다음으로 제일 큰값을 반복적으로 선택하는 것이다. 그러므로 4, 7, 3이 된다. 하지만 4, 7, 2, 10을 선택해야 제일 큰값을 가질수있다. 이와 같이 일반적으로 탑욕법은 최적의 해을 보장할 수 없을 때가 많다.
하지만 특정 문제에서 탑욕 알고리즘을 통해 최적의 해를 보장 받을수 있다. 다음 예제를 통해 알아보자.

Python 예제:

# n = 기본 값, k = 나눌 값
n, k = map(int, input().split())

# 수행 횟수
result = 0

while True:
    # n이 k로 나누어 떨어지는 수가 될 때까지 빼기
    # 첫번쩨 loop에서 소수점은 무시됨으로 target = 16
    # 두번째 loop에서 target = 4
    target = (n // k) * k
    result += (n - target)
    n = target

    # n이 k보다 작을때 (더 이상 나눌 수 없을 때) 반복문 탈출
    if n < k:
        break
	
    # k로 나누기    
    # 두번째 loop에서 target = 4
    n //= k
    result += 1


# 마지막 loop에서 수행한 것이 없기에 남은 횟수에 대하여 1을 빼기
result += (n - 1)
print("정답: " + str(result) + "번")

👆🏼의 예제는 입력 받은 값의 최소의 수로 원하는 값을 구할 수 있도록 구현되어 있다. 입력 받은 값 n을 k로 나누거나 1로 빼는 과정을 최소 몇번을 반복해야 1의 값이 되는지 수행 횟수를 찾는 문제이다. 여기서 k는 n으로 꼭 나누어 떨어져야 소수를 피할 수 있다. 그리고 k로 나누는 것이 1로 빼는 것보다 n를 빨리 줄일수 있으므로 최적의 해를 구할 수 있다.
위 예제는 시간 복잡도 logN을 갖는다.