Denoising with Sparsity

Sparsity란 뭘까에 대해서는 이전 포스트에 제가 보기에 (나름..) 직관적으로 정리해두었다.

Sparsity는 주어진 데이터가 대부분 0으로 이루어짐을 의미한다. 이러한 Sparse data를 만들기 위해 주어진 현실의 데이터를 적절한 space로 보내서 만들 수 있다.

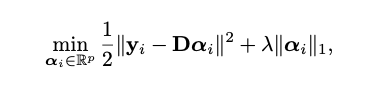
이러한 작업은 보통 위와 같은 optimization problem을 풀면 얻어질 수 있다. 여기에서 $y$는 주어진 데이터이고, $D$는 해당 space의 basis들의 집합, 그리고 $\alpha$는 sparse coefficient이다.

Basis들의 집합인 $D$는 관점에 따라 다르게 부를 수 있다. Dictionary Learning 관점에서는 Dictionary이고, Space의 관점으로 보면 Basis라고 불리기도 한다. (그리 중요한 내용은 아니다.)

위의 식을 잘 보면 regularization term으로 L1 Norm이 들어가있는데 이는 L1 Regularization의 변수선택 성질을 통해 Sparsity를 구현하기 위함이다. 이에 대해서는 LASSO 논문에 잘 나와있기도하고, 블로그나 교육자료 pdf 등에 워낙 자주 다루니까 넘어가겠다.

이런 L1 Regularization을 쓰는 이유는 Sparsity와 동일한 의미인 L0 Regularization의 경우 LP-Hard이기 때문..

근데 이런 Sparsity는 어디에 쓰려고 그러는걸까.. 이전 포스트에서는 Compressed Sensing에 사용되는 것을 언급했다. 근데 이 Sparsity는 Compressed Sensing 뿐만 아니라 Denoising에 사용될 수 있다.

위의 Optimization Problem을 다르게 봐보자.
$y$는 noisy image라고 해보자.
위의 최적화 문제는 Sparsity에 대한 Regularization이 들어가있기 때문에 완전히 0의 값을 내놓지는 못할 것이다. (Regularization이 없었을때 Global optima)
즉, 문제 해결 후 최적화된 $D\alpha$는 $y$와 동일하지 않다는 것이다. 그럼 어떻게 다를까?

아주 간단한 예시로 $D$를 Fourier Basis라고 생각해보자. 그러면 $\alpha$는 Fourier coefficient일 것이다. 이런 Fourier Coefficient가 Sparse하게 표현된다는 것은 필요한 frequency에 대한 정보만 가져다 쓰겠다는 것이다.(최대한 $y$와 비슷한 결과를 내놓으면서.) 그럼 $D\alpha$는 어떻게 생겼을까?
이미지의 주된 정보는 소수의 Low Frequency 성분으로 이루어져있고, detail한 정보는 다수의 High Frequency로 이루어져있다. 이는 Fourier Space에서 High Frequency Information을 없애도 비슷한 결과가 나온다는 것으로부터 알 수 있다. (이전 포스트 :https://velog.io/@yhyj1001/Sparsity-%ED%98%84%EC%8B%A4-%EC%84%B8%EA%B3%84%EC%9D%98-%EB%8D%B0%EC%9D%B4%ED%84%B0%EB%A5%BC-%EB%8B%A4%EB%A5%B4%EA%B2%8C-%EB%B0%94%EB%9D%BC%EB%B3%B4%EC%9E%90의 Example부분에 나와있다.)
그리고 noisy image에서의 Noise는 High Frequency 성분으로 이루어져있다. (노이즈는 값이 급격히 변하기 때문)
그러니까 $\alpha$를 대부분 0의 값을 갖도록 하고 $y$와 최대한 비슷한 결과를 만들어내기 위해서 Noise를 제거하는 방향으로 학습될 것이다.
Sparsity를 활용한 Denoising은 이런식으로 진행된다.

BM3D

이 논문은 진짜 짜증나는 논문이었다. Traditional method라서 방법도 복잡하고 글도 빽빽하다. 그래도 Traditional Denoising Method에서 아주 중요한 논문이라 꾸역꾸역 읽었다. ㅋㅋ

Abstract

Sparsity는 2D Image를 Grouping해서 3D Block을 통해 enhance 될 수 있다.
그러니까 주어진 이미지를 Grouping 해서 3D block으로 만들고 Sparsity를 통해 denoising 후 다시 2D Block으로 만들자는게 이 논문의 요지이다.

"Sparsity는 2D Image를 Grouping해서 3D Block을 통해 enhance 될 수 있다." 이 말은 무슨 의미일까.
이미지를 패치화 했다고 생각해보자. 이 패치 이미지들을 비슷한 것들끼리 그룹을 지어보면 이 그룹의 데이터는 Low rank data일 것이다. (비슷하다는 거는 dependent하다는 거고, rank는 independent에 대한 것이니까)
즉 grouping 하면 비슷한 이미지들끼리 모일거고 이는 Low rank data이기 때문에 Sparse하게 잘 표현이 될 것이라는 것을 뜻한다. 이를 Sparsity가 Enhance 된다고 표현한 것이다.

이 논문에서 제안한는 것은 "A novel image denoising strategy based on an enhanced sparse representation"이다. 이런 방법을 통해 Denoising을 하겠다는 것이다. ㅇㅇ

중요한 것은 noise의 sigma를 알고 zero mean을 따른다고 가정한다는 것이다.

Method

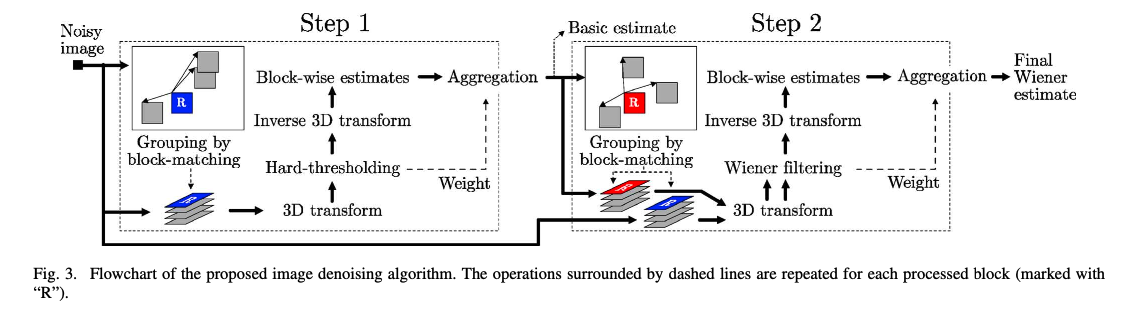
본 논문의 Flowchart이다. 크게 두 step으로 나뉜다. 첫번째 Process에서 일차적으로 denoising하고 두번째에서 첫번째 정보를 통해 적절히 denoising한다고 생각하면된다.
그리고 세부 프로세스는 세 step으로 나뉜다. (Block Matching, Collaborative Filtering, Aggregation)
Block Matching은 비슷한 패치끼리 모아가지고 그룹으로 만드는 것이고 Collaborative Filtering은 L1 constraint를 통한 Optimization problem을 풀었던 것과 같이 image를 Denoising 하는 것이다. Collaborative Filtering이라고 부르는 이유는 비슷한 데이터를 모은 그룹 안에서 실행해서 그런 것 같다.

Grouping

Grouping은 비슷한 것들을 모아서 3D 형태의 데이터로 만드는 것을 의미한다. (grayscale 이미지라고 가정한 경우 group은 여러 2d data가 모여있기 때문에 3D라고 볼 수 있다.)
Grouping은 Kmeans clustering이나 Vector Quantization을 통해 얻어질 수 있다. 그런데 이런 clustering 같은 경우 disjoint group을 만들고 동일 cluster 내에서 데이터에 따라 영향력이 다르게 된다. (중앙에서 멀수록 관련 없는..) 이런 경우 한 cluster 내에서 영향이 적은 데이터는 이 해당 cluster 내에만 속해있기 때문에 이에 대한 정보를 거의 고려해주지 못한다.
이러한 문제가 있으니까 다른 방법을 찾아봐야한다.
이에 대한 해결책으로 Block Matching을 사용한다. Block Matching은 어떤 Reference image 기준으로 distance가 특정 임계값 아래인 것을 동일 group이라고 설정하는 작업이다. 여기에서 distance의 기준을 어떻게 설정하냐에 따라 다른 결과가 나올 수 있다.

Collaborative Filtering

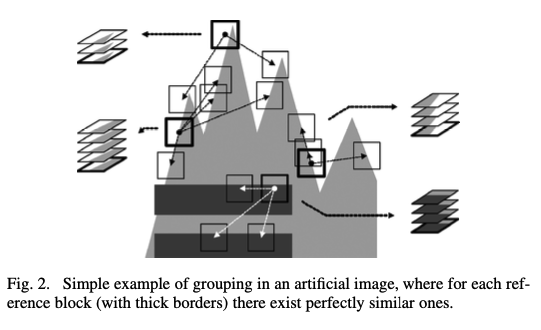
위 이미지를 봐보자. 이런 간단한 형태의 이미지가 주어졌을때 Grouping을 하는 것을 보여준다. 이 이미지는 매우 간단한 이미지라 grouping 시 완전 동일한 데이터가 중복될 수 있다. 여기에서 주어진 이미지는 zero-mean noise가 더해진 noisy 이미지이고 grouping된 group이 완전 동일한 이미지들로 이루어져있다고 가정하면, 단순히 각 group에 대해 평균 취해버리면 깨끗한 이미지가 나오게 된다. (zero mean noise 였으니까) 이런걸 Collaborative Filtering이라고 한다.

근데 이런 가정은 현실 세계에서 거의 있을 수 없다. 다른 방법이 필요하다.
-> 이를 해결하기 위해 Sparsity를 도입하는 것이다.

Aggregation

앞 프로세스에서 패치화된 이미지들을 원래 이미지로 보내는 것이다. 이를 위해 앞 과정에서 position 정보를 유지해줘야한다.
앞서 언급했듯 Block Matching을 사용하게 되면 Overlap되는 데이터가 많아진다. (중복되는.)
이와 같이 동일한 위치이면서 다른 Group에 해당되는 Blocks은 적절한 Weights를 통해 평균을 취해주면 된다.
뒤에서 자세히 설명하겠다.

Alogrithm

전체적인 프로세스는 아래와 같다.

• Basic Estimate
  • Block Matching
  • Collaborative Hard-Threshold Filtering (3D Transform -> HT -> Inverse 3D Transform)
  • Aggregate
• Final Estimate
  • Block Matching
  • Collaborative Wiener Filtering
  • Aggregation

위의 과정을 차근차근 설명해보겠다.

Basic Estimate에서의 Block Matching

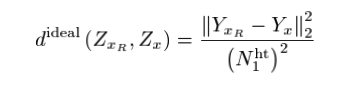
우리가 Block Matching을 하기 위해선 적절한 distance를 정의해야한다. 그리고 비슷한 이미지를 모으기 위해서는 아무래도 Noisy Image보다는 Clean Image로 하는게 더 정확할 것이다. 그러니까 Ideal한 경우를 먼저 살펴보자.
위의 식의 notation을 설명하자면
$Z_{x_R}$ : $x_R$은 reference patch의 위치를 의미하며, $Z_{x_R}$는 해당 reference에 대한 Noisy Block이다 (Group).
$x$는 임의의 위치를 의미한다.
$Y_{x_R}$ : $Z_{x_R}$와 같은 의미이지만 Clean Block을 의미한다.
$N_1^{ht}$ : basic estimate process의 patch size이다.

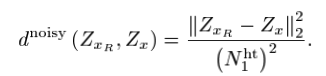
하지만 우리는 Noisy image밖에 없기 때문에 noisy한 distance 밖에 구하지 못한다.
이 Noisy distance 좀 분석해보자.

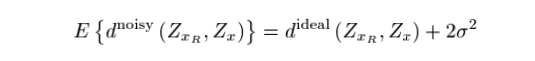
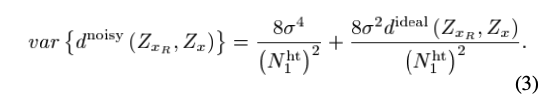
이 noisy distance에 대한 expectation과 variance를 구하면 이와 같은데 variance를 잘 보면 noise의 sigma와 pixel size의 크기 감소에 대해 variance가 크게 커짐을 알 수 있다.
이런 variance가 큰 distance를 사용할 경우 Block matching의 성능이 너무 안좋을 수 있다.
그러니까 다른 distance를 정의하자.

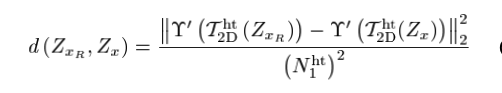
새로 정의된 distance는 이와 같다. $\Gamma'$은 hard thresholding을 의미하고, $\Tau^{ht}_{2D}$는 normalized linear 2D Transform을 의미한다.
이게 무슨 의미냐면 Fourier Space 같은 적절한 space로 옮긴 다음 hard thresholding을 거쳐서 어느정도 정제된 결과에 distance를 구하겠다는 것이다. 물론 변환된 space에서의 coefficient에 대한 거리를 구하게 된다. 논문에서는 이를 d-distance라고 부른다.
Hard thresholding은 $\lambda_{2D}\sigma$을 통해 수행된다.

여기에서 굳이 Inverse transform을 수행하지 않은 이유는 $\Tau^{ht}_{2D}$가 Orthogonal matrix이면 scale과 angle을 유지하기 때문에 이런 distance 결과는 동일할 것이기 때문이다.

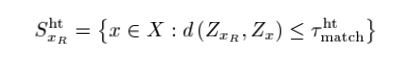
그래서 위와 같이 사전에 정의된 block matching threshold $\tau^{ht}_{match}$로 Grouping을 진행한다.
여기에서 S는 위치 즉 indices set이라고 생각하면 된당.

이제 Block Estimate 과정에서의 Grouping을 마쳤다.

이 논문이 골때리는건 읽을건 되게 많은데 다 읽고나면 별게 없는 것 처럼 느껴진다..

Basic Estimate의 Collaborative Filtering

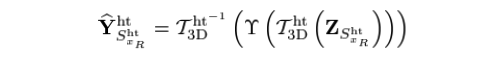
이 과s^{ht}정은 별게 아니다. (Notation은 되게 짜증난다.)
$Z^{ht}_{x_R}$은 $x_R$ 위치 기준 reference에 대한 3D noisy block (group)을 의미한다.
Grouping된 noisy block에 DCT와 같은 normalized 3D linear transform을 적용하고 sparsity를 고려해주기 위해 coefficient에 hard thresholding을 적용한다. 그리고 다시 원래 space로 되돌리는 것이다.
이를 통해 일차적으로 denoise된 이미지를 얻을 수 있다.

Aggregation은 Basic, Final Estimate 모두 동일해서 나중에 한번에 말하겠다~

Final Estimate의 Block Matching

앞서 1차적으로 basing estimate를 거치면서 denoise를 적용했다. 그러니까 이제 굳이 d-distance를 사용하지 않아도 괜찮다
그냥 l2 distance를 적용한다.

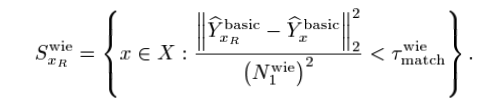
근데 특이한 점은 위와 같이 일단 index set을 가져오고 Basic Estimate에 대해 Block Matching을 적용하는 것 뿐만 아니라 원래의 Noisy patches에 대해서도 Block Matching을 적용한다는 것이다.

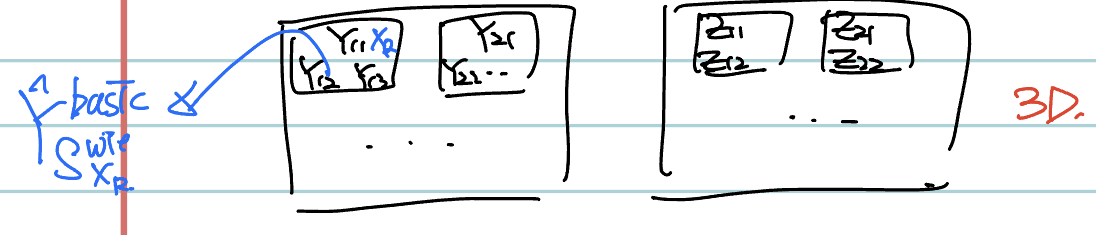
그래서 이딴식으로 나온다. Y는 Basic Estimate에 대한 Block Matching 결과이고 Z는 Noisy patches에 대한 Block matching 결과이다.

이 Y를 가지고 Wiener shrinkage coefficient라는 것을 정의해서 Z에 대해 Collaborative Filtering 할거다.

Final Estimate에서의 Collaborative Filtering

일단 앞서 언급했듯이 Wiener Shrinkage Coefficient를 정의하자.
손이 너무 아파서 그냥 캡쳐해왔당 ㅋㅋ

$\Tau^{wie}_{3D}$는 적절한 3D Transform(ex:DCT)이다. 이 식이 의미하는 바는, Basic Estimated Block을 $\Tau^{wie}_{3D}$을 사용하여 coefficient 형태로 변환했을때 이 coefficient의 크기가 크면 sigma의 영향이 낮기 때문에 weight를 높게 설정하고 coefficient의 크기가 작으면 sigma의 영향 또한 크기 때문에 weight를 높게 설정하는 것이다.

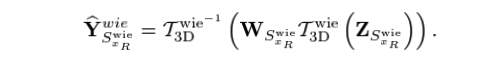
이제 이 weights를 기반으로 위처럼 final estimated block을 만들 수 있다. ㅇㅇ

Aggregation

위의 Basic Estimate, Final Estimate의 결과 block들을 원래 위치로 모아주면 된다. 이를 위해 이전 과정에서 position 정보는 유지해준다. (block coordinate information : $x$)

앞서 언급했듯 Block matching을 하면 한 block이 여러 group에 속하는 경우가 발생한다. 이를 위해 단순히 동일 위치에 대한 평균을 취해버리면 되겠지만 본 논문에서는 좀 더 효과적인 방법을 제안한다.
일단 적절한 aggregation weights를 구하고 이에 대한 weighted average를 취한다.

Aggregation Weights

논문에서 실험적으로 발견한 사항 : 해당 Block의 sample variance에 반비례하도록 weight를 부여하면 좋다. Sample Variance가 크면 좋은 Group이라고 볼 수 어렵다 (비슷하지 않은 데이터가 모인거니까). 그렇기 때문에 sample variance의 역수를 사용하면 된다.

근데 그럼 sample variance를 어떻게 구해야하는가?

1. Block Estimate의 Sample variance : $\sigma^2 N^{x_R}_{har}$
2. Final Estimate의 Sample variance : $\sigma^2||W_{S^{wie}_{x_R}}||^2_2$

노테이션이 골때린다. 처음 딱 마주하면 논문 읽을 의지를 없애버린다. 좀 간단하게 쓰지..
$\sigma^2$는 noise의 variance이고 $N^{x_R}_{har}$은Collaborative Filtering 과정에서 hard thresholding 적용한 뒤의 non-zero coefficient의 개수이다.
$||W_{S^{wie}_{x_R}}||^2_2$는 Wiener Filter Coefficient이다.

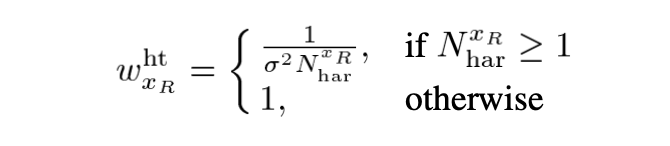
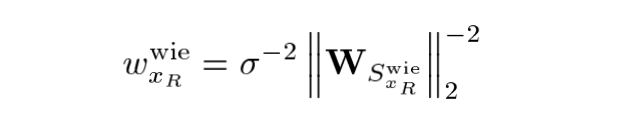
즉, Basic Estimate와 Final Estimate에 대한 weights는 대충 이렇게 설정하면 된다. (분산에 반비례하니까~)

Weighted Average

이제 동일 위치에서 여러 그룹에 속해 있는 경우에 위의 weights를 사용하여 모아주면 된다.

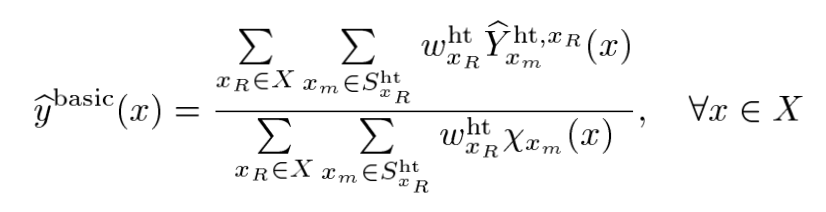
여기에서 $\chi$는 $x$가 $x_m$에 있는지에 대한 function이다. 동일한 위치의 Block만 고려한 개수를 사용하겠다는것이다.

기타 등등.

Wiener Filter?

신호처리 분야에서 사용되는 Wiener Filter를 computational imaging 분야의 denoising에 접목시켜서 사용한다는건 어떤 의미일까..

이런 간단한 psf(kernel)에 대해 균일한 Motion Blur가 있다고 가정해보자. 여기에서 * 의 의미는 convolution이다. 이 convolution operator는 Fourier Domain에서 단순 multiplication이 되기 때문에 Fourier Space로 보내고 PSF in Fourier 로 나눠버리면 원래 데이터를 구할 수 있게된다. 이를 deconvolution이라고 한다.
근데 단순히 나눈다는 것은 굉장히 위험하다. 왜냐면 0인 값이 존재할 경우 발산해버리기 때문에..

이 경우를 봐보자. 이는 위와 같은 motion blur에 noise가 더해진 것이다. 이제 이를 위와 같이 Fourier space로 보내서 나누는 작업을 한다면 아래와 같은 결과가 나온다.

노이즈가 amplified 되었다.. 이 이유는 Deconvolution 시, Noise가 더해진 degraded image $g(x,y)$는 noise 때문에 굉장히 high frequency 성분이 많을 것이고 $h(x,y)$는 low pass filter와 동일하기 때문에 low frequency 성분이 많을 것이다.
그러니까 이를 Fourier Space에서 $g(x,y)/h(x,y)$ 이렇게 deconvolution 해버리면 high frequency 성분이 굉장히 강조된다.
그러니까 위 사진과 같이 노이즈가 듬뿍 들어간 결과가 나오는 것이다.

이런 상황을 해결하기 위해 Wiener deconvolution을 사용할 수 있다.

손이 아프니까 그냥 내가 수식으로 적은 그림을 가져왔다. Wiener Deconvolution의 경우 위와 같은 closed form을 갖는데 잘 보면 Noise Signal Ratio (SNR) term이 있음을 알 수 있다. 근데 N은 노이즈에 해당하는 Fourier space에서의 값이고 F는 True image에 대한 Fourier space에서의 값이다. 이 둘은 알 수 없는데 대충 적절한 constraint로 둘 수 있다.

이 식을 잘 보면 Low pass filter $H$가 작을 경우 []안의 Term이 매우 작아진다. 그래서 매우 큰 $1/H$ 값을 $[]$ 안의 Term으로 보상해줄 수 있게 된다. 이를 통해 적절한 Deconvolution을 수행할 수 있게된다.

본 논문에서 사용한 Wiener Coefficient 또한 Noise Signal과 True Signal의 비율을 사용하여 보상하기 위한 형태이기 때문에 이런 이름을 붙이지 않았나 생각이 든다~

Border Effect

본 논문에서 제안하는 방법은 Patch 단위로 잘라놓은 다음 적절한 filtering을 거치고 다시 하나의 이미지로 붙이는 것이기 때문에 붙여놓은 결과는 다소 이상할 수 있다. patch의 경계면이 보이는 등등..
그러니까 post processing이 필요하다
본 논문에서는 kaiser window를 가지고 sliding window해서 이를 해결한다