
이걸 왜 갑자기
지금까지 작성한 글은 sparsity에 대한 내용을 다뤘다. (2개밖에 안되긴 함ㅋㅋ)
근데 오늘 적을 내용은 Optimization 방법론에 관한 내용이다. 근데 이걸 왜 갑자기 소개하는걸까
이전 포스트들을 보면 Sparsity를 고려해주기 위해 L1 Regularization을 사용하는 것을 알 수 있다. L1 regularization의 변수 선택 성질로 인해 Sparsity 비스무리한 효과를 보일 수 있다.
L1 Regularization이 들어간 Optimization problem을 세웠다고 생각해보자.
이런 식이 있다. 여기에서 y는 측정된 Noisy data이고 D는 임의의 Dictionary이다. (Basis)
이러한 최적화 문제를 품으로써 Optimal sparse code 를 구할 수 있다는 것이다. 근데 이런 Optimization problem은 어떻게 풀어야하는 것일까.
일단 위의 식에서 가 주어진 상태라면 에 대해서 minimization을 취해주면 된다. 그리고 이는 Convex optimization problem이다. 하지만 L1에 대한 gradient는 불분명하므로 Gradient descent 방법을 사용하기가 어렵다. (미분 불가능한 지점이 존재하니까..)
(물론 당연히 subgradient 로 정의해주면 된다)
Sparsity에 대해서 알면 뭐하나.. 문제를 풀 수 없는데..
그래서 ISTA를 소개하려고 한다.
Proximal Gradient Descent
ISTA를 이해하기 위해선 Proximal Gradient Descent를 알아야한다. Proximal Gradient Descent를 위의 L1 regularization이 포함된 최적화 문제에 적용한게 ISTA다.
Proximal Gradient Descent는 위의 최적화 문제와 같이 non differentiable function을 differentiable part와 non-differentiable part로 나눌 수 있는 상황에 사용하는 방법이다.
아주 간단한다.
를 최소화 하는 최적화 문제를 위와 같이 정의해보자. differentiable part (), non-differentiable part ()로 표현하고 두 변수 가 같다는 condition을 주었다.
변수가 두개니까 일단 x에 대해서 gradient descent를 취해보자.
그러면 일단 를 최소화 하는 방향으로 한 step 나아간게 된다.
그리고 에 대한 문제를 풀어보자.
이 식은 condition이었던 변수 간 거리를 minimization term 안으로 넣어준 것이다
이처럼 non-differentiable term에 대한 minimization을 proximal operator 라고 한다.
여기에서 minima를 구하기 위해 subgradient의 정의를 사용한다. (non differentiable function의 미분을 정의하기 위해)
이 과정을 간단하게 말하자면
일단 differentiable한 term에서 gradient descent step을 하고 그 후에 non differentiable term을 최소화 할 수 있으면서 gradient step을 진행했던 점과 가까운 거리의 점으로 나아가는 것이라고 할 수 있다.
ISTA
이제 원래 우리가 논의하던 L1 Regularization이 들어간 Sparse coding 최적화 문제로 돌아가보자.
위에서 언급한 순서대로 1. Differentiable function에 대한 gradient descent 2. updated point에서 non-differentiable function을 minization하면서 원래 위치와의 거리를 최소화 하는 방향으로 움직인다.
이 식에 대해서는 전형적인 form으로 나타낼 수 있다.
1번 식은 명확한 form으로 나왔다.
그럼 2번 식은 어떻게 나타날까?
subgradient에 대한 optimality condition을 소개한다.
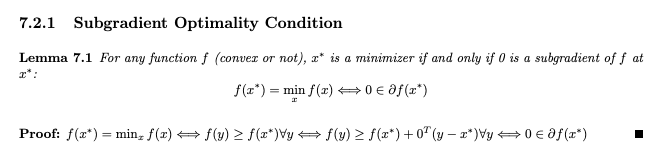
optimal point에서 non-differentiable한 경우 subgradient를 정의하면 해당 점에서의 subgradient는 0인 값을 갖는다는 것이다.
subgradient는 미분 불가능한 점에서 구간 형태로 정의되기 때문에 subgradient가 0이라는 것은 장담할 수 없기 때문에 subgradient set 안에 0이 들어있다는 것으로 정의를 세웠다.
이를 기반으로 문제를 풀어보자..
미분을 깔끔하게 하기 위해 1/2 곱해줬다.
Subgradient optimality condition을 통해 이와같이 표현할 수 있다.
,
L1 norm에 대한 subgradient는 위의 식과 같다. 이제 이 경우들에 대해 식을 나눠 생각해보면 아래와 같은 식으로 정리 할 수 있다.
이 식들과 조건을 만족하는 가 proximal operation의 정답이므로 이를 각 부호에 대해 분해해서 생각해보면 아래와 같은 식으로 정리할 수 있다. 이건 알아서 생각해보자.
사실 이걸 생각해보는게 핵심이다. 필자의 능력과 의지 부족으로 이걸 하나하나 기술하지 못했다... (ㅋㅋ..)
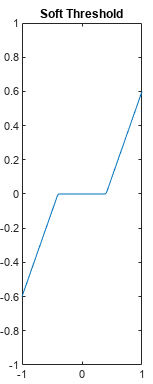
L1 regularization에 대한 proximal operation의 결과는 위와 같은 Soft thresholding과 동일하다.
그러니까 proximal operator는 gradient 이런거 필요 없고 그냥 soft thresholding 적용하면 된다는 뜻이다.
결론은
1. L2 Term (Differentiable Term)에 대한 Gradient Descent
2. Soft Threshoding
하면 식에 대한 optimization이 된다는 것이다. 이걸 ISTA라고 부른다.
Learning ISTA (LISTA)
Learning ISTA는 위의 ISTA를 Learnable Encoder를 통해 훈련하여 근사해보자는 것이다.
근사해놓은 encoder를 사용한다면 inference가 빠르게 된다.
일단 Encoder는 로 정의하겠다. w는 encoder의 파라미터이다.
그리고 Encoder를 학습하기 위한 Loss function은 아래와 같다.
여기에서 는 관측된 데이터의 개수이고 는 이에 대응하는 optimal sparse code이다. 즉, 이걸 훈련하려면 에 대응하는 를 알고 있어야한다.
이 식은 ISTA로도 풀 수 있다.
하지만 ISTA는 이 를 한번에 업데이트 하기 때문에 내부 요소들 간의 관계성을 파악하지 못한다.
예를 들어보자.
Dictionary 의 첫번째, 두번째 row가 아주 비슷한 angle과 magnitude를 갖고, 주어진 데이터가 첫번째 row와 더 비슷하다고 해보자. 여기에서 ISTA를 적용하여 update하면 둘 다 높은 값을 띄게 될 것이다 (동시에 update 되니까). 근데 이런 현상은 Interpretability를 제한한다. 정말 Sparsity 성질에 맞게 나타내려면 첫번째 row에 대응하는 coefficient가 더 높은 값을 내놓아야한다.
이런 현상이 발생하는 이유는 내부 요소들 간의 관계성을 파악하지 못하기 때문이다.
이런 문제를 논문에서는 "Mutual Inhibition and Explanation away"라고 말을 한다.
위와 같은 문제를 해결하는 방법은 아주 간단하다.
CoD (Coordinate descent)를 사용하는 것이다. 이는 내부의 요소들을 한번에 업데이트 하는게 아닌 Loss 수치가 가장 큰 요소만을 업데이트 하는 것이다. 그리고 이 업데이트를 여러번 수행하여 전체적으로 Loss를 가장 낮게하는 방향으로 나아가게 된다.
논문에서 algorithm에 대해 수도코드로 잘 보여주고 있지만 본 포스트에서 사용한 notation과 굉장히 상이한 notation을 사용하고 있기 때문에 그냥 안가져왔다.
어쨌든 우리는 학습 과정에서 정답 데이터로 사용될 optimal sparse code를 어떻게 구하는가에 대해서 알게 되었다.
그럼 학습은 어떻게 진행되는걸까?
일단 라는 녀석이 등장한다 이고, mutual inhibition matrix라고 부른다.
그리고 Filter matrix 이다.
이를 통해서 ISTA 식을 재정의 할 수 있다.
은 초기 값을 나타낸다.
ISTA 식을 위처럼 나타냈고, 위에서 를 Learnable Parameter로 정의한다. 알다시피 는 soft thresholding의 파라미터이다.
그래서 Encoder를 위와 같은 parameter와 식을 계산하는 function으로 구성해주면 된다.
이를 통해 전에 소개했던 object function을 최소화하는 방향으로 update해나간다.
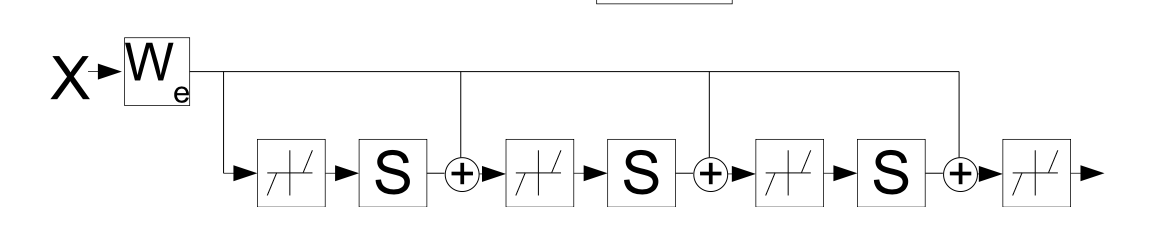
여기에서 는 라고 생각하면 된다.
중요한 것은 이 LISTA가 recurrent 한 형식을 띄고 있다는 것이다.
일단 논문에서 소개된 방법은 이와 같다.
하지만 필자가 여러 코드들을 찾아봤는데 몇몇 코드는 논문에서 제시한 방법과는 다소 상이해보였다.
어떤 코드들은 sparse code를 대상으로 훈련을 한다기보다는 그냥 pair 형태의 train data를 가져와서 그냥 알고리즘만 recurrent한 LISTA 형식을 차용하여 input data를 ground truth data에 피팅하는데 사용된다.
이건 필자가 독학하다보니 잘못 이해한 것일 수도 있다.