
Linked List
In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains: data, and a reference (in other words, a link) to the next node in the sequence.
by Wikipedia
링크드 리스트란 노드라는 기본 요소를 사용해 선형적인 데이터 묶음을 추상적으로 표현한 것이다. 노드에는 데이터뿐만 아니라 다음 노드를 가리키는 참조(링크)가 포함되어 있다.
어디에 사용하면 좋을까?
링크드 리스트는 일련의 데이터를 차례대로 저장하지만 배열과 달리 실제 메모리 상에서 연속적인 위치에 저장하지 않는다. 다음 노드를 가리키는 참조를 사용해 유연하게 데이터를 할당한다.
배열은 처음이나 중간 지점에 데이터를 추가하거나 삭제하려면 모든 요소를 이동시켜야 하지만 링크드 리스트는 참조(링크)만 변경하면 되므로 데이터의 추가나 삭제가 빈번한 경우에 사용된다. 주식 호가창을 예로 들 수 있다.
Singly Linked List
이 글에서는 링크드 리스트 중 단일 링크드 리스트에 대해서만 다루고자 한다. 구체적인 구조를 그림을 통해 살펴보자.
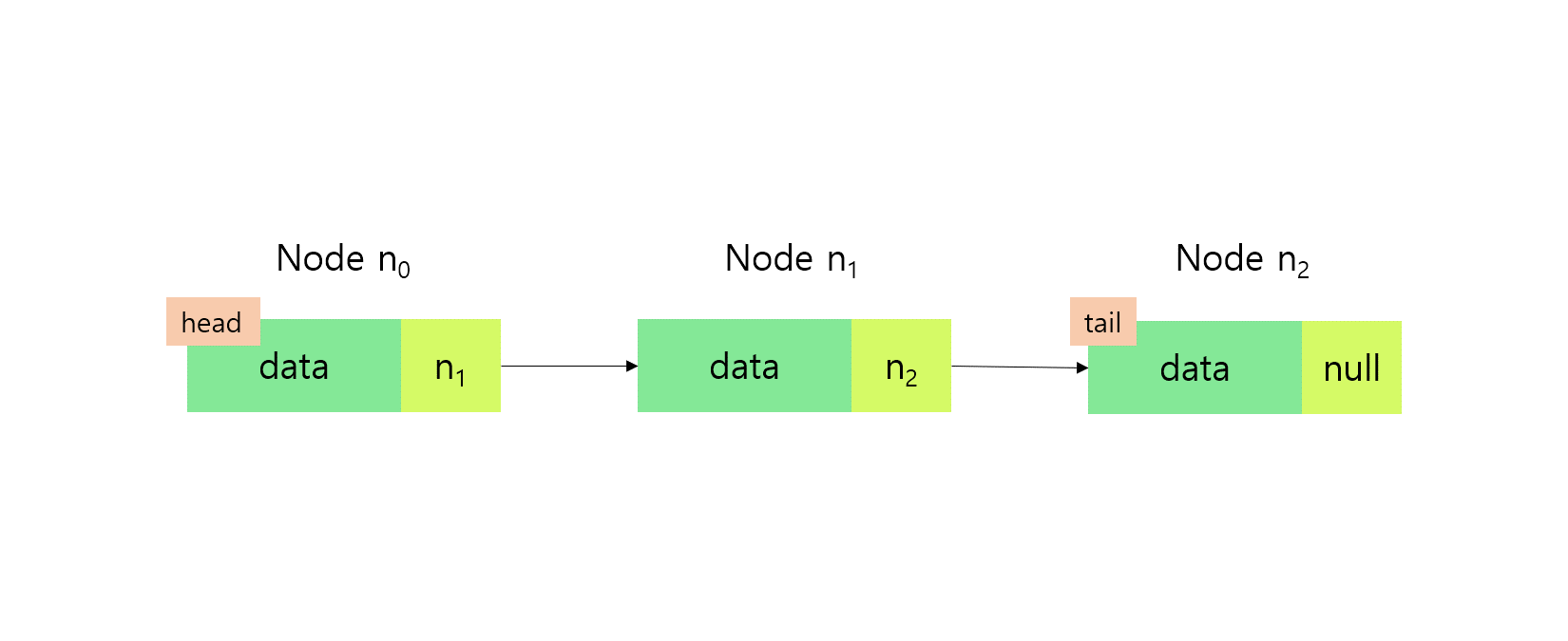
Node:data와pointer로 이루어진 요소로서 모여서 리스트를 형성data: 데이터pointer(link): 다음Node를 가리키는 참조head: 가장 앞에 있는Nodetail: 가장 끝에 있는Node
TypeScript로 구현해보자
📦 codesandbox에서 전체 코드를 확인하고 실습해볼 수 있습니다.
타입스크립트의 제네릭을 활용해 원하는 타입의 데이터를 담을 수 있는 링크드 리스트를 만들어보자.
Node
먼저 Node를 만든다.
- val:
data를 담는다. - next: 다음 노드를 가리키는
pointer다. 다음 노드가 없으면 null 값을 가진다.
type Node<T> = {
val: T;
next: Node<T> | null;
};Linked List 인터페이스
다음으로 구현하고자 하는 링크드 리스트의 인터페이스를 정의한다.
- getAtIndex(): 전달받은 인덱스 위치에 있는 노드의 데이터를 가져온다. 인덱스가 리스트의 범위를 벗어난 경우 null을 반환한다.
- addAtHead():
head에 노드를 추가한다. - addAtTail():
tail에 노드를 추가한다. - addAtIndex(): 전달받은 인덱스 위치에 노드를 추가한다. 인덱스가 리스트의 범위를 벗어난 경우 노드를 추가하지 않는다.
- deleteAtIndex(): 전달받은 인덱스 위치에서 노드를 삭제한다. 인덱스가 리스트의 범위를 벗어난 경우 노드를 삭제하지 않는다.
- size: 리스트의 길이를 반환한다.
interface ILinkedList<T> {
getAtIndex(index: number): T | null;
addAtHead(val: T): void;
addAtTail(val: T): void;
addAtIndex(index: number, val: T): void;
deleteAtIndex(index: number): void;
size: number;
}Linked List 클래스
- head: null로 초기화한다.
- _size: 0으로 초기화한다.
- size: _size의 getter 메서드이다.
class LinkedList<T> implements ILinkedList<T> {
constructor(private head: Node<T> | null = null, private _size: number = 0) {}
/**
* Time: O(1)
*/
public get size() {
return this._size;
}
// ...
}- getNodeAtIndex()
전달받은 인덱스 위치에 있는 노드를 찾아 반환하는 메서드이다. 인덱스가 리스트의 범위를 벗어날 경우 null을 반환한다. 이 메서드는 다른 메서드에서 노드를 찾기 위해 사용되므로 클래스 내에서만 접근할 수 있도록 private으로 설정한다.
/**
* Time: Worst - O(n), Best - O(1)
*/
private getNodeAtIndex(index: number): Node<T> | null {
if (index < 0 || index >= this.size) {
return null;
}
let curr = this.head; // head에서 출발한다.
let count = 0;
while (count < index) { // index-1 노드에 도달할 때까지 반복
curr = curr!.next; // 현재 노드에서 다음 노드로 이동한다.
count++;
}
// while문이 종료되면 index 노드가 curr에 담긴다.
return curr; // 이 노드를 반환한다.
}- getAtIndex()
전달받은 인덱스에 있는 노드의 데이터를 반환하는 메서드이다.
/**
* Time: Worst - O(n), Best - O(1)
*/
getAtIndex(index: number): T | null {
const node = this.getNodeAtIndex(index); // index 노드를 가져온다.
if (node) { // 노드가 있으면
return node.val; // 그 노드의 데이터를 반환한다.
}
return null; // 노드가 없으면 null을 반환한다.
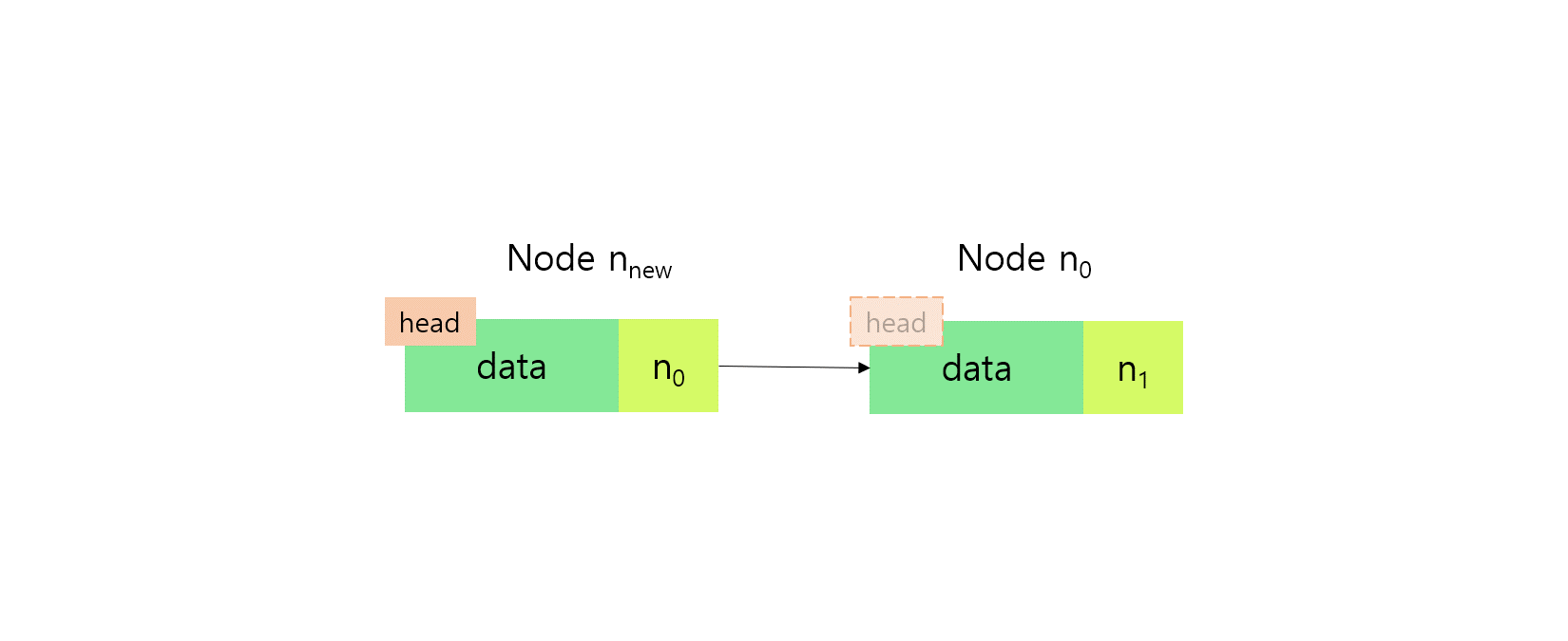
}- addAtHead()
리스트의 맨 앞에 노드를 추가하는 메서드이다.
/**
* Time: O(1)
*/
addAtHead(val: T): void {
// 기존 head를 가리키는 새로운 노드를 만들고 이를 head로 바꾼다.
this.head = { val, next: this.head };
this._size++; // 리스트의 사이즈를 하나 증가시킨다.
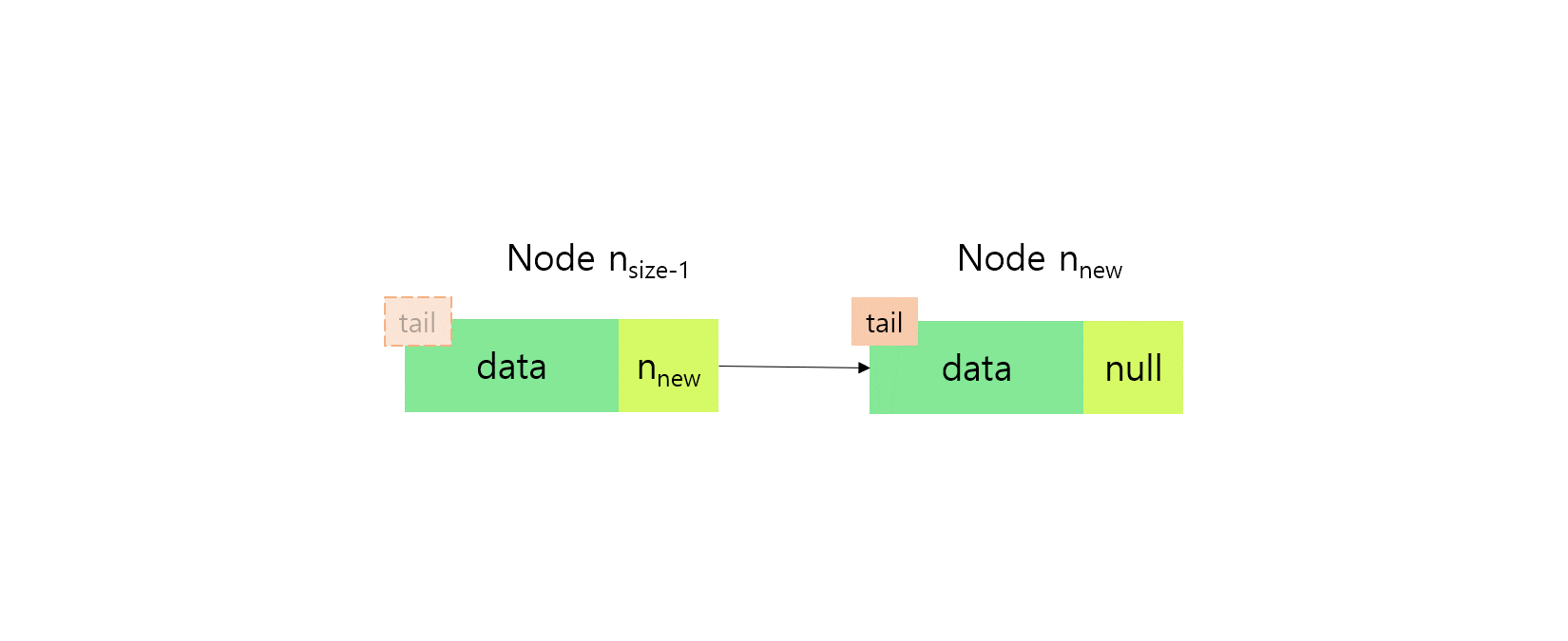
}- addAtTail()
리스트의 맨 끝에 노드를 추가하는 메서드이다.
/**
* Time: Worst - O(n), Best - O(1)
*/
addAtTail(val: T): void {
if (this.size === 0) { // 리스트가 비어 있으면
this.addAtHead(val); // 리스트의 맨 앞에 노드를 추가한다.
return;
}
const lastNode = this.getNodeAtIndex(this.size - 1)!; // tail을 가져온다.
lastNode.next = { val, next: null }; // 기존 tail이 새로 만든 노드를 가리키도록 하여 이를 tail로 바꾼다.
this._size++; // 리스트의 사이즈를 하나 증가시킨다.
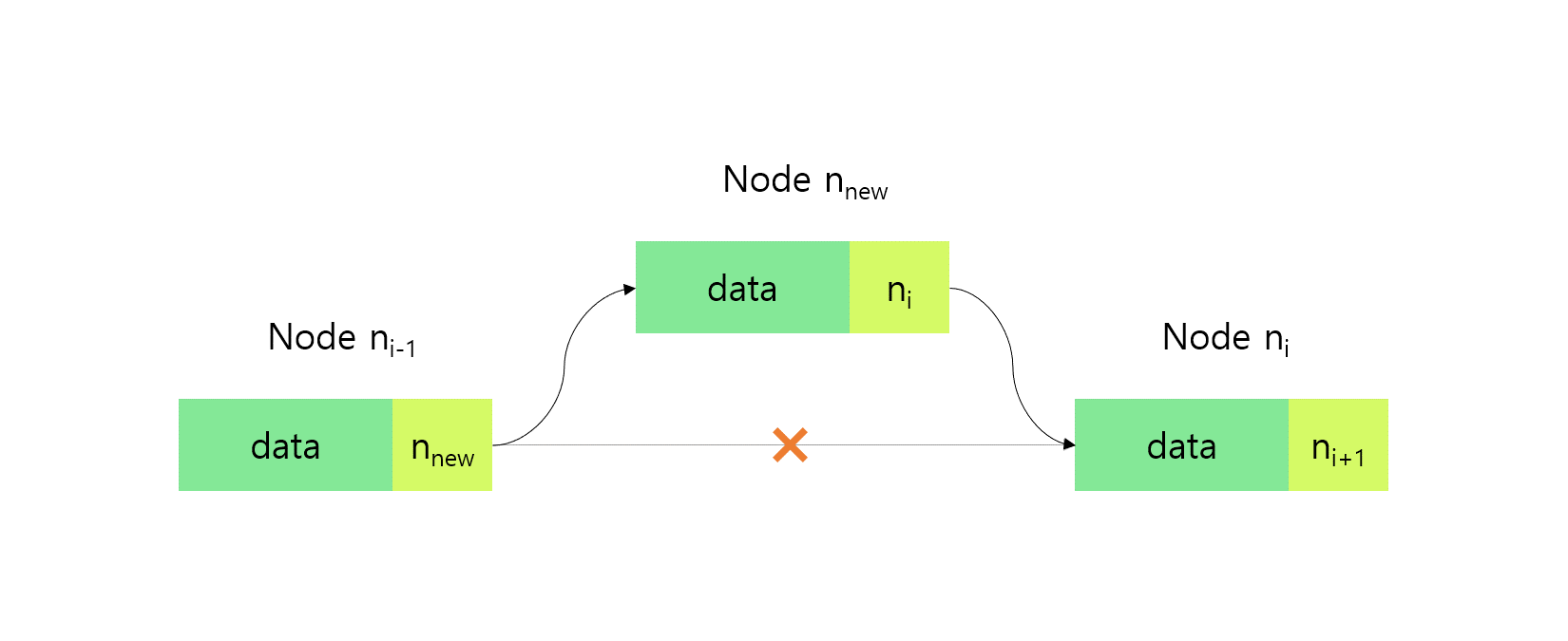
}- addAtIndex()
전달받은 인덱스 위치에 노드를 추가하는 메서드이다.
/**
* Time: Worst - O(n), Best - O(1)
*/
addAtIndex(index: number, val: T): void {
if (index < 0 || index > this.size) {
return;
}
if (index === 0) { // 리스트가 비어 있으면
this.addAtHead(val); // 리스트의 맨 앞에 노드를 추가한다.
return;
}
const prevNode = this.getNodeAtIndex(index - 1)!; // index-1 노드를 가져온다.
// 새로운 노드를 만들고 index 노드를 가리키도록 한다.
// index-1 노드는 이 새로운 노드를 가리키도록 한다.
prevNode.next = { val, next: prevNode.next };
this._size++; // 리스트의 사이즈를 하나 증가시킨다.
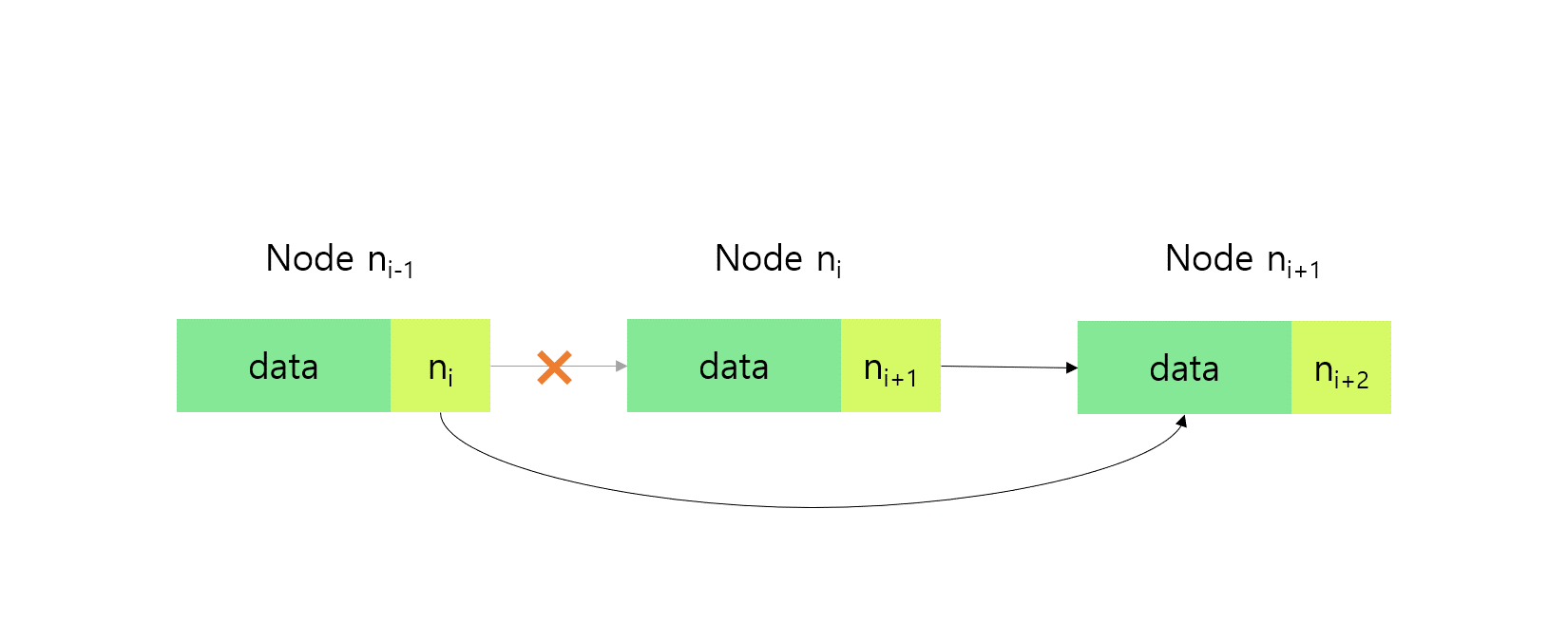
}- deleteAtIndex()
전달받은 인덱스 위치에서 노드를 삭제하는 메서드이다.
/**
* Time: Worst - O(n), Best - O(1)
*/
deleteAtIndex(index: number): void {
if (index < 0 || index >= this.size) {
return;
}
if (index === 0) { // 맨 앞에 있는 노드를 삭제하는 경우
this.head = this.head!.next; // head의 다음 노드를 head로 바꾼다.
} else { // 그렇지 않은 경우
const prevNode = this.getNodeAtIndex(index - 1)!; // index-1 노드를 가져온다.
prevNode.next = prevNode.next!.next; // index-1 노드가 index+1 노드를 가리키도록 한다.
}
this._size--; // 리스트의 사이즈를 하나 감소시킨다.
}보충학습
📢 Big-O 표기법을 소개하고 Array와 Linked List의 차이점을 비교해봅니다.
Time Complexity
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm.
by Wikipedia
시간 복잡도란 알고리즘의 실행 시간을 수치화한 것이다.
Big-O Notation
In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows.
by Wikipedia
그리고 Big-O 표기법은 시간 복잡도를 나타내는 방법 중 하나인데 최악의 경우를 고려하는 표기법이다. 다시 말해서 아무리 오래 걸려도 이 시간 내에는 끝난다는 뜻이다.
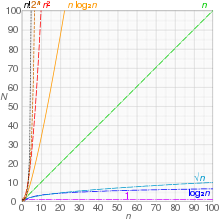
- O(1): 실행시간이 입력 크기에 의존하지 않는다. 상수 시간이 걸린다.
- O(n): 실행시간이 입력 크기에 따라 선형적(linear)으로 증가한다. 입력 크기에 비례하는 시간이 걸린다.
Array vs Linked List
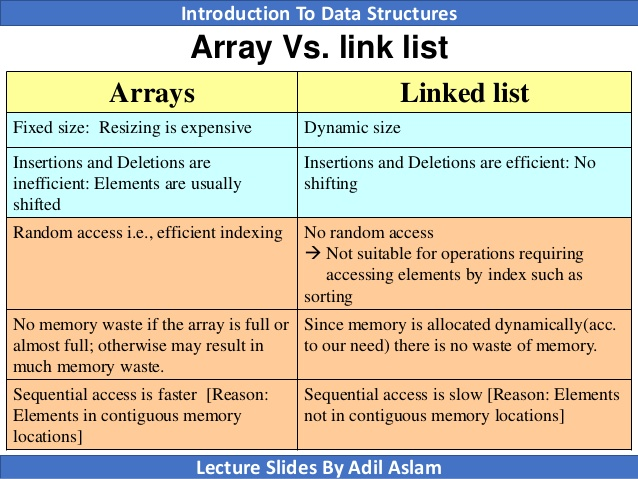
참고자료
잘못된 부분에 대한 지적은 언제든 환영합니다! 😉
