CNN의 역사

1957년

• Frank Rosenblatt가 Mark I Perceptron machine 을 개발했다
• 이 기계는 "perceptron"을 구현한 최초의 기계이다
• "Perceptron"은 Wx + b 와 유사한 함수를 사용한다
• 하지만 여기에서는 출력 값이 1 또는 0이다
• 여기에서도 가중치 W를 Update 하는 Update Rule이 존재한다
• 이 Update Rule은 Backpropagation과 유사했다

Perceptron

• 인공신경망의 가장 간단한 형태로, 이진 분류 문제를 해결하기 위해 사용되는 알고리즘이다
• 작동방식
  • 퍼셉트론은 여러 개의 입력을 받아 각각의 가중치를 곱한다
  • 이 값들을 모두 합한 후, 편향(bias)을 더한다
  • 그 결과를 활성화 함수(대개는 계단 함수)에 통과시켜 최종 출력을 만든다
• 퍼셉트론은 이러한 과정을 통해 주어진 입력에 대해 두 가지 클래스 중 하나를 예측한다
• 퍼셉트론은 간단하고 계산 효율성이 뛰어나지만, 선형적으로 분리할 수 없는 데이터에 대해서는 잘 작동하지 않는다는 한계가 있다

1960년

• Widrow와 Hoff가 Adaline and Madaline을 개발했다
• 이는 최초의 Multilayer Perceptron Network 이었다
• 이 시점에서야 비로소 Neural network와 비슷한 모양을 하기 시작하긴 했지만 아직 Backpropagation 같은 학습 알고리즘은 없었다

1986년

• 최초의 Backporp은 1986에 Rumelhart가 제안하였다
• Chain rule과 Update rule을 확인할 수 있다
• 이때 최초로 network를 학습시키는 것에 관한 개념이 정립되기 시작했다
• 하지만 그 이후로 NN을 더 크게 만들지는 못했다
• 그리고 한동안은 새로운 이론이 나오지 못했고 널리 쓰이지도 못했다

2006년

• Geoff Hinton 과 Ruslan Salakhutdinov의 2006년 논문에서 DNN의 학습가능성을 선보였고, 그것이 실제로 아주 효과적이라는 것을 보여주었다. 하지만 그 때 까지도 아직 모던한 NN는 아니었다
• backprop이 가능하려면 아주 세심하게 초기화를 해야했다
• 그래서 여기에서는 전처리 과정이 필요했고, 초기화를 위해 RBM을 이용해서 각 히든레이어 가중치를 학습시켜야 했다
• 이렇게 초기화된 히든 레이어를 이용해서 전체 신경망을 backprop하거나 fine tune하는 것이었다

2012년

• NN의 광풍이 불기 시작했다
• NN이 음성 인식에서 아주 좋은 성능을 보였다
• 이는 Hintin lab에서 나온 것인데 acoustic modeling과 speech recognition에 관한 것이었다
• 또한 2012년에는 Hinton lab의 Alex Krizhevsky에서
  영상 인식에 관한 landmark paper가 하나 나왔다
• 이 논문에서는 ImageNet Classification에서 최초로 NN을 사용했고, 결과는 정말 놀라웠다
• AlexNet은 ImageNet benchmark의 Error를 극적으로 감소시켰다
• 그 이후로 ConNets은 아주 널리 쓰이고 있다

CNN이 유명해진 역사

1950년

• Hubel과 Wiesel이 일차시각피질의 뉴런에 관한 연구를 수행했다
• 고양이의 뇌에 전극을 꽂고 고양이에게 다양한 자극을 주며 실험을 했다
• 이 실험을 통해 뉴런이 oriented edges와 shapes같은 것에 반응한다는 것을 알아냈다. 그리고 이 실험에서 내린 몇 가지 결론은 아주 중요했다
• 그중 하나는 바로 피질 내부에 지형적인 매핑(topographical mapping)이 있다는 것이다
  • 피질 내 서로 인접해 있는 세포들은 visual field내에 어떤 지역성을 띄고 있다
• 또한 이 실험에서 뉴런들이 계층구조를 지닌다는 것도 발견했다
  • 다양한 종류의 시각자극을 관찰하면서 시각 신호가 가장 먼저 도달하는 곳이 바로 Retinal ganglion 이라는 것을 발견했다
    • Retinal ganglion cell은 원형으로 생긴 지역이다
  • 가장 상위에는 Simple cells이 있는데, 이 세포들은 다양한 edges의 방향과 빛의 방향에 반응했다
  • 그리고 더 나아가, 그런 Simple Cells이 Complex cells과 연결되어 있다는 것을 발견했다
    • Complex cells는 빛의 방향 뿐만 아니라 움직임에서 반응했다
    • 복잡도가 증가함게 따라, 가령 hypercomplex cells은 끝 점(end point) 과 같은것에 반응하게 되는 것이다
• 이런 결과로부터 "corner" 나 "blob"에 대한 아이디어를 얻기 시작한 것이다

1980년

• neocognitron은 Hubel과 Wiesel이 발견한 simple/complex cells의 아이디어를 사용한 최초의 NN이다
• Fukishima는 simple/complex cells을 교차시켰다
• Simple cells은 학습가능한 parameters를 가지고 있고, Complex cells은 pooling과 같은 것으로 구현했는데 작은 변화에 Simple cells보다 좀 더 강인하다

1998년

• Yann LeCun이 최초로 NN을 학습시키기 위해 Backprob과 gradient-based learning을 적용했고, 실제로 그 방법은 문서인식에 아주 잘 동작했다
• 우편번호의 숫자를 인식하는데도 아주 잘 동작했다
• 하지만 아직 이 Network를 더 크게만들 수는 없었다

2012년

• Alex Krizhevsky가 CNN의 현대화 바람을 일으켰다. 이 Network는 AlexNet이라고도 불린다
• Yann LeCun의 CNN과 크게 다르진 않다. 다만 더 크고 깊어졌다
• 가장 중요한 점은 지금은 ImageNet dataset과 같이 대규모의 데이터와 발전된 GPU의 성능을 활용할 수 있다는 것이다

CNN의 활용

• 이미지 검색에 정말 좋은 성능을 보이고 있다
• 학습된 특징이 유사한 것을 매칭시키는데 아주 강력하다
• Detection에서도 ConvNet을 사용한다
  • 영상 내에 객체가 어디에 있는지를 아주 잘 찾아낸다
  • 버스나 보트 등을 찾아내고 네모박스를 정확하게 그린다
• segmentation은 단지 네모박스만 치는 것이 아니라 나무나 사람 등을 구별하는데 픽셀 하나 하나에 모두 레이블링하는 것이다
• 대부분의 작업은 GPU가 수행할 수 있으며, 병렬처리를 통해 ConvNet을 아주 효과적으로 훈련하고 실행시킬 수 있다
• ConvNets을 비디오에도 활용할 수 있는데, 단일 이미지의 정보 뿐만 아니라 시간적 정보도 같이 활용가능하다
• 또한 pose recognition도 가능하다. 어깨나 팔꿈치와 같은 다양한 관절들을 인식해 낼 수 있다
• 의학 영상을 가지고 해석을 하거나 진단을 하는 데에도 이용할 수 있다
• 또한 은하를 분류하거나 표지판을 인식하는데도 쓰인다
• 항공지도를 가지고 어디가 길이고 어디가 건물인지를 인식하기도 한다
• Image Captioning같은 이미지가 주어지면 이미지에 대한 설명을 문장으로 만들어 내는 것도 가능하다

Fully Connected Layer

• 신경망에서 주로 사용되는 계층 중 하나로, 각 노드가 이전 계층의 모든 노드와 연결되어 있는 계층이다
• 이 계층에서는 각 노드의 입력 값에 가중치를 곱하고 편향을 더한 후 활성화 함수를 적용하여 출력 값을 생성한다
• 보통 신경망의 마지막 부분에 위치하여, 이전 계층에서 추출한 특성을 바탕으로 최종적인 예측을 만드는 역할을 한다
• 최종 스코어를 계산하기 위해 사용한다

Convolutional Layer

• 입력 이미지에 합성곱 연산을 적용하여 다양한 특징을 추출한다
• 이 연산은 특정 크기의 필터(또는 커널)를 입력 데이터에 슬라이딩하면서 적용되며, 이 필터는 이미지의 특정 특징(예: 가장자리, 색상, 질감 등)을 감지하는 역할을 한다
• Convolution Layer와 기존의 FC레이어의 주된 차이점이 있다면 Convolution Layer는 기존의 구조를 보존시킨다는 것이다
• 기존의 FC Layer가 입력 이미지를 길게 쭉 폈다면 이제는 기존의 이미지 구조를 그대로 유지하게 된다
• 필터는 입력 데이터(예: 이미지)에 적용되는 작은 윈도우 또는 커널이다
• 이때, 필터의 각 요소와 해당 요소가 커버하는 입력 데이터 사이에는 가중치를 곱하고, 이들을 모두 합하여 하나의 출력 값을 생성한다
• 필터의 각 요소가 곧 학습 가능한 가중치이므로, 학습 과정에서는 이 가중치들이 역전파를 통해 업데이트된다. 이를 통해 모델은 특정 특징을 더 잘 감지하기 위한 최적의 가중치를 찾아가게 된다
• 이 필터는 이미지를 슬라이딩하면서 공간적으로 내적을 수행하여 Feature Map 또는 Activation Map이 출력으로 나오게 된다
• 합성곱 연산은 이러한 지역적인 특징을 유지하면서도, 필터의 파라미터 공유와 스트라이드(Stride)를 통한 다운샘플링 등으로 인해, 고차원의 입력 데이터를 효율적으로 처리할 수 있게 해준다
• 필터는 입력의 깊이(Depth)만큼 확장된다

슬라이딩

• Convolution은 이미지의 좌상단부터 시작하게 된다
• 필터의 각 자리의 값과 필터와 겹쳐진 이미지의 각 자리의 값과 내적을 수행하고 그 값들을 모두 더한다. 이 결과값이 출력 데이터의 해당 위치의 값이 된다
• 연산을 수행한 후 오른쪽 또는 아래로 미리 지정된 Stride만큼 이동하여 연산을 수행한다
• 이렇게 하나의 필터를 가지고 전체 이미지에 Convolution 연산을 수행한다
• 그러면 Feature Map 또는 Activation Map이라는 출력값을 얻게 된다
• 이러한 과정을 통해, 필터는 입력 데이터의 지역적인 특징을 추출하는 역할을 한다
• 보통 Convolution Layer에서는 여러개의 필터를 사용한다. 왜냐하면 필터마다 다른 특징을 추출하고 싶기 때문이다

Activation Funcion

• 인공 신경망의 뉴런에서 출력 값을 결정하는 함수
• 뉴런의 출력이 다음 레이어로 전달되는 값을 결정하며, 비선형성을 도입하여 모델의 표현력을 증가시킨다

활성화 함수 종류

• 시그모이드 함수(Sigmoid Function)
  • 이 함수는 출력을 0과 1 사이로 제한한다
  • 이는 확률을 나타내는 데 유용하지만, 그래디언트 소실 문제(Vanishing Gradient Problem)를 일으킬 수 있다
• 하이퍼볼릭 탄젠트 함수(Tanh Function)
  • 이 함수는 출력을 -1과 1 사이로 제한한다
  • 시그모이드 함수보다 더 넓은 출력 범위를 가지기 때문에, 종종 더 좋은 성능을 보인다
• 렐루 함수(ReLU Function)
  • 이 함수는 음수 입력에 대해 0을 출력하고, 양수 입력에 대해 입력 그대로를 출력한다
  • 이는 계산이 간단하고 그래디언트 소실 문제를 완화하는 데 도움이 되어, 현재 가장 널리 사용되는 활성화 함수이다
• 리키 렐루 함수(Leaky ReLU Function)
  • 이 함수는 음수 입력에 대해 매우 작은 양수 기울기를 가지고, 양수 입력에 대해 입력 그대로를 출력한다
  • 이는 렐루 함수의 '죽은 렐루' 문제를 해결하는 데 도움이 된다
• 소프트맥스 함수(Softmax Function)
  • 이 함수는 출력을 확률 분포로 변환한다
  • 이는 다중 클래스 분류 문제에서 출력 레이어의 활성화 함수로 주로 사용된다

Pooling

• 주로 Feature Map 또는 Activation Map의 크기를 줄이거나 주요한 특징을 강조하는 데 사용한다
• 특징 맵을 작은 영역(예: 2x2)으로 나눈 후, 각 영역에서 특정 값을 선택하여 새로운, 축소된 특징 맵을 생성한다

Pooling의 종류

• Max Pooling
  • 각 영역에서 가장 큰 값 선택
  • 영역 내의 가장 두드러진 특징을 유지하며, 동시에 특징 맵의 크기를 줄인다
• Average Pooling
  • 각 영역의 평균값 선택
  • 영역 내의 전반적인 특징을 유지하며, 특징 맵의 크기를 줄인다

Pooling의 이점

• 차원 축소
  • 풀링을 통해 특징 맵의 크기를 줄이면, 모델의 파라미터 수가 줄어들어 연산량이 감소하고 과적합을 방지할 수 있다
• 이동 불변성
  • 풀링은 이미지 내의 객체가 약간 이동하더라도 비슷한 특징 맵을 생성하므로, 모델의 이동 불변성을 증가시킨다
• 특징 강조
  • 맥스 풀링은 가장 두드러진 특징을 강조하여, 이를 통해 객체 인식 성능을 향상시킬 수 있다

Spatial dimension

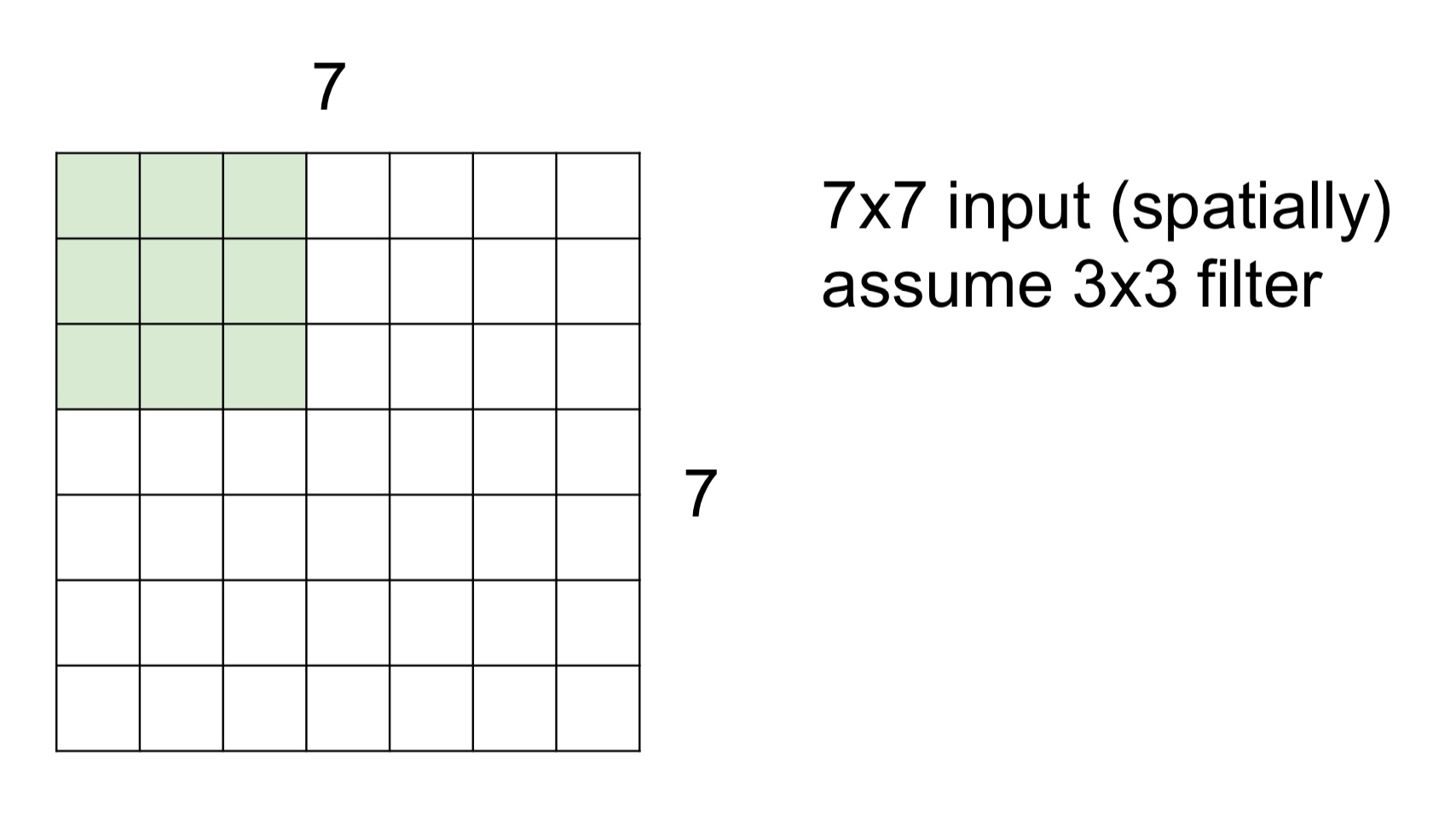
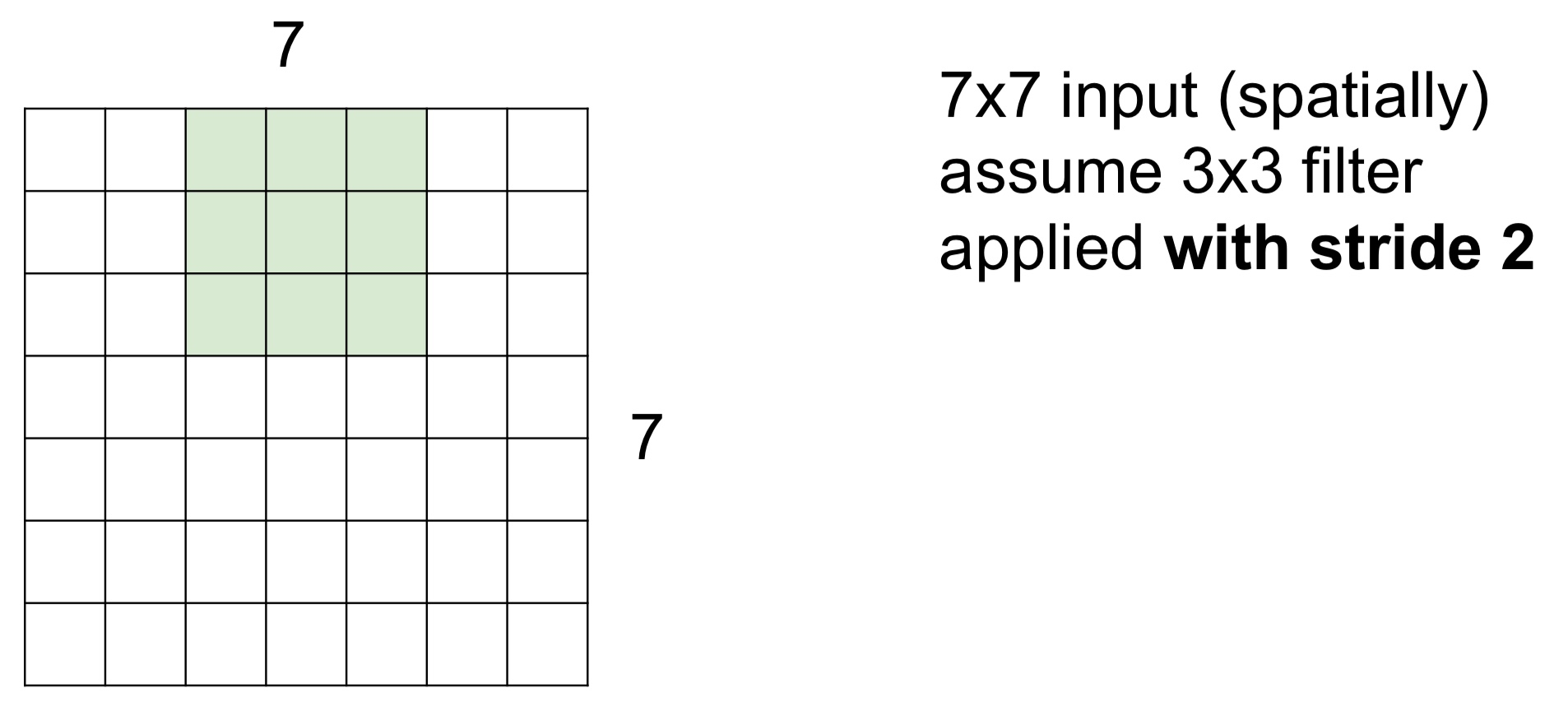
• 위 이미지처럼 7x7 입력에 3x3 필터가 있을 때, 필터를 좌상단에 위치시키고 해당 원소값들끼리 내적을 수행하고 값들을 모두 더한 값을 구한다
• 이 값들은 Feature Map 또는 Activation Map의 좌상단에 위치한다

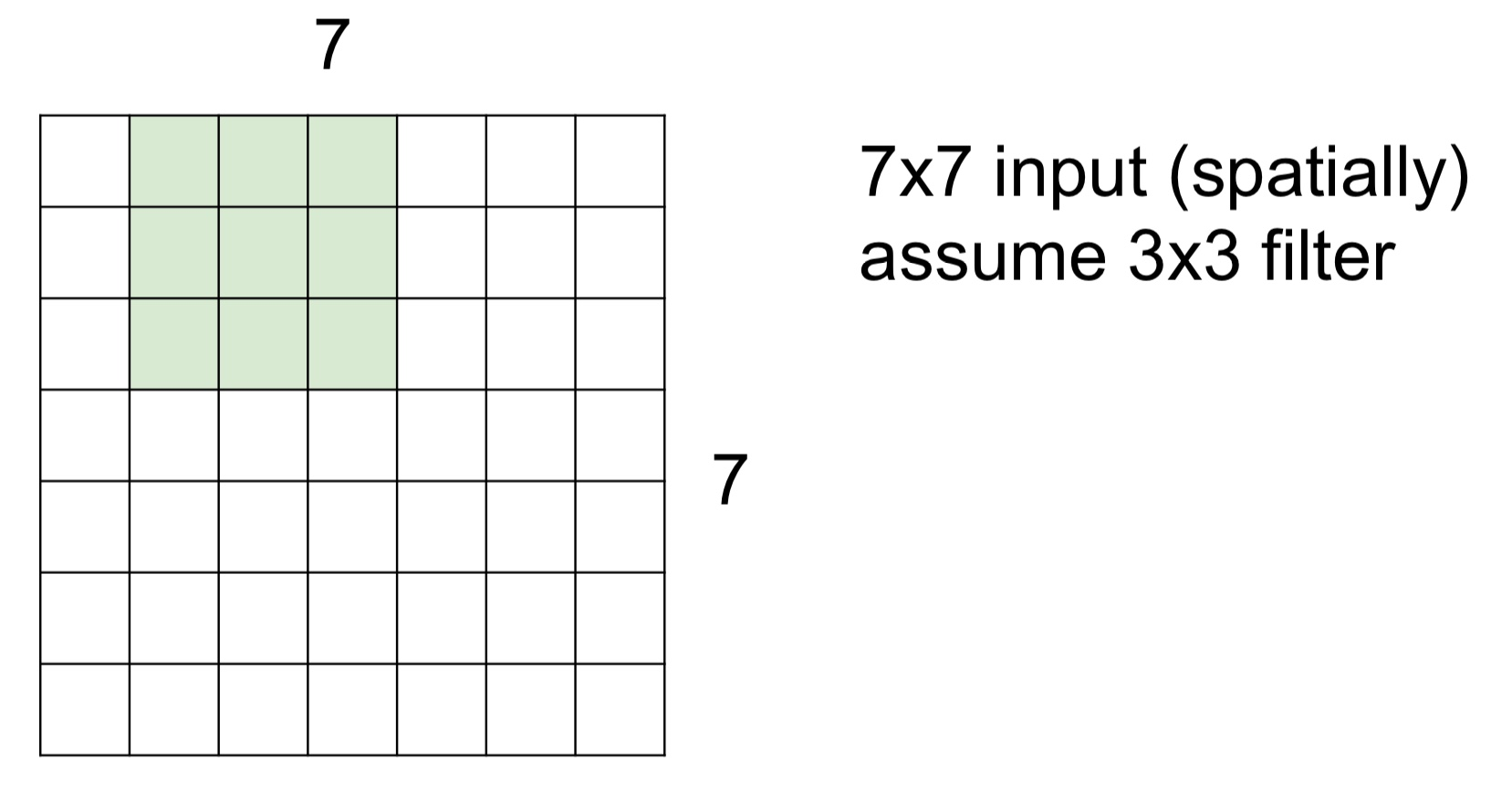
• Stride = 1 이라고 한다면, 연산을 하고 오른쪽으로 한 칸 움직인다. 이동한 칸에서 다시 연산을 수행한다

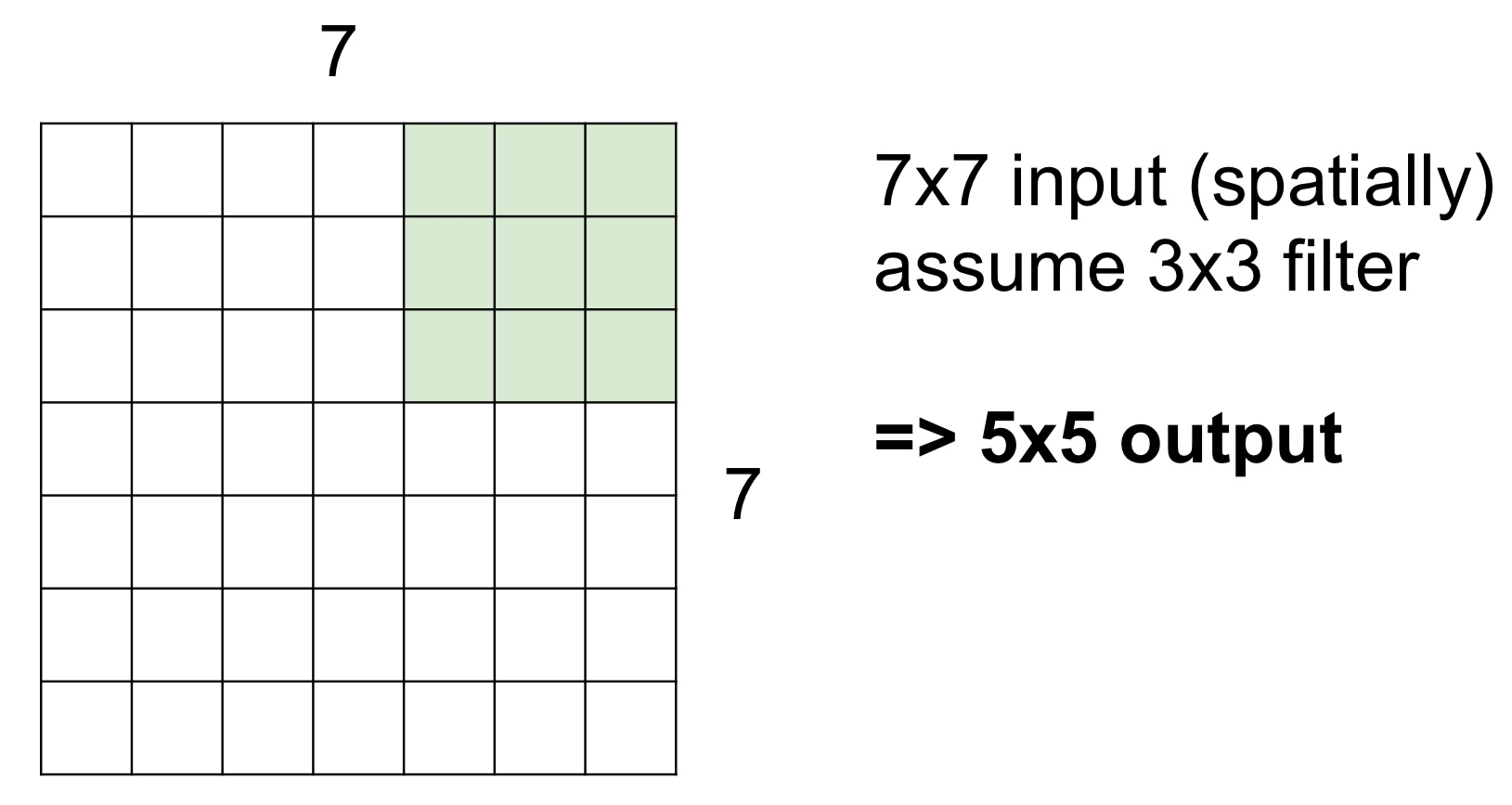
• 이렇게 계속 반복하다보면 결국 5x5의 Feature Map 또는 Activation Map을 얻게 된다

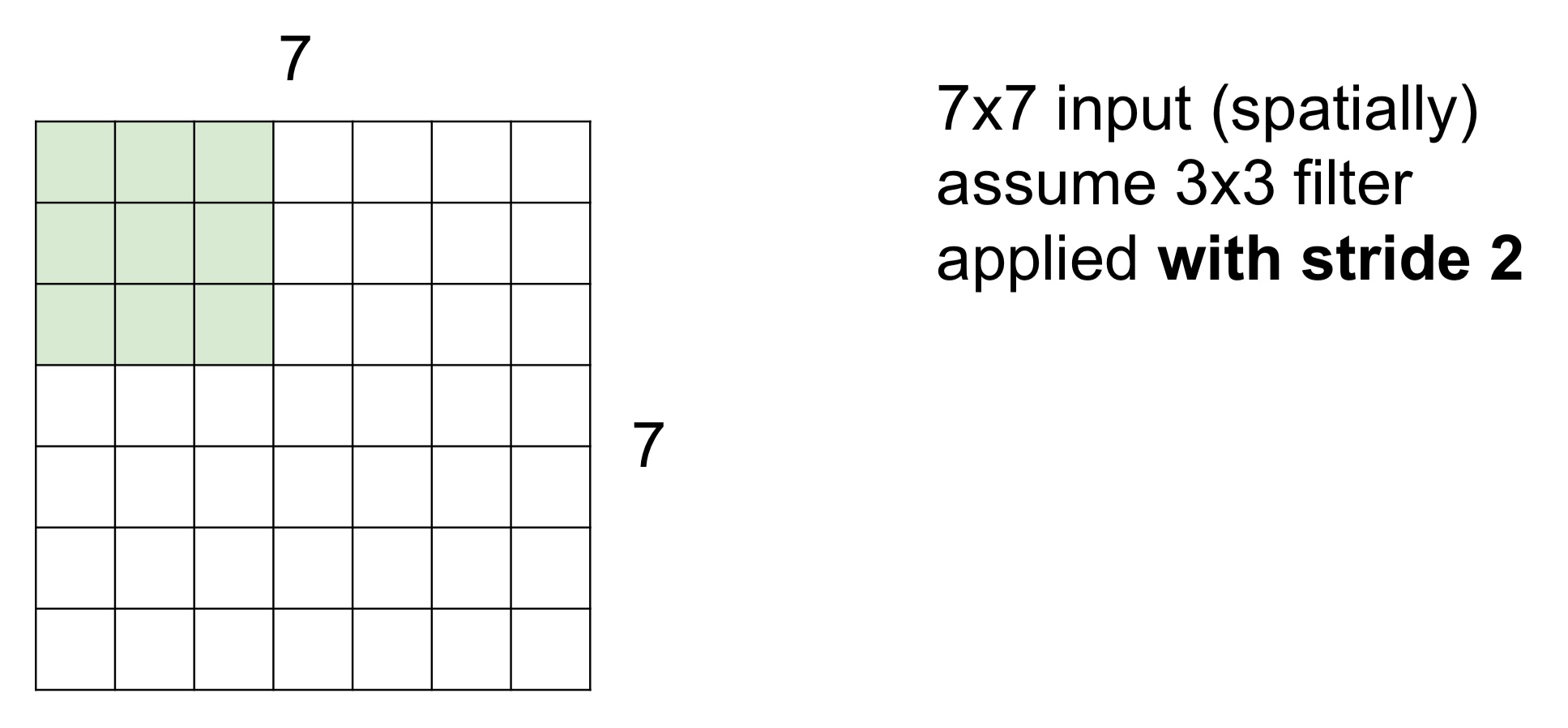
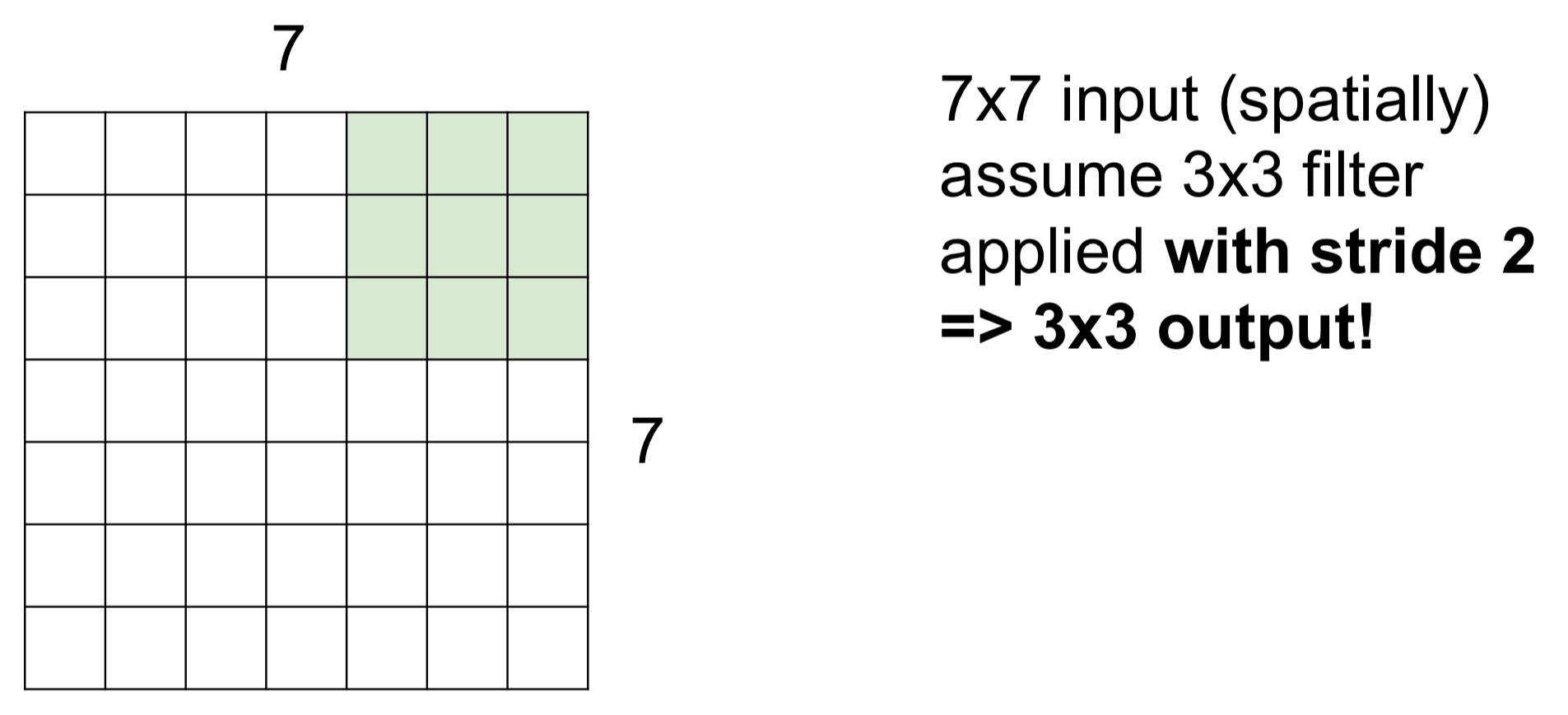
• Stride = 2일 때는 2칸씩 이동하면서 최종적으로는 아래 이미지처럼 3x3의 Feature Map 또는 Activation Map을 얻게 된다

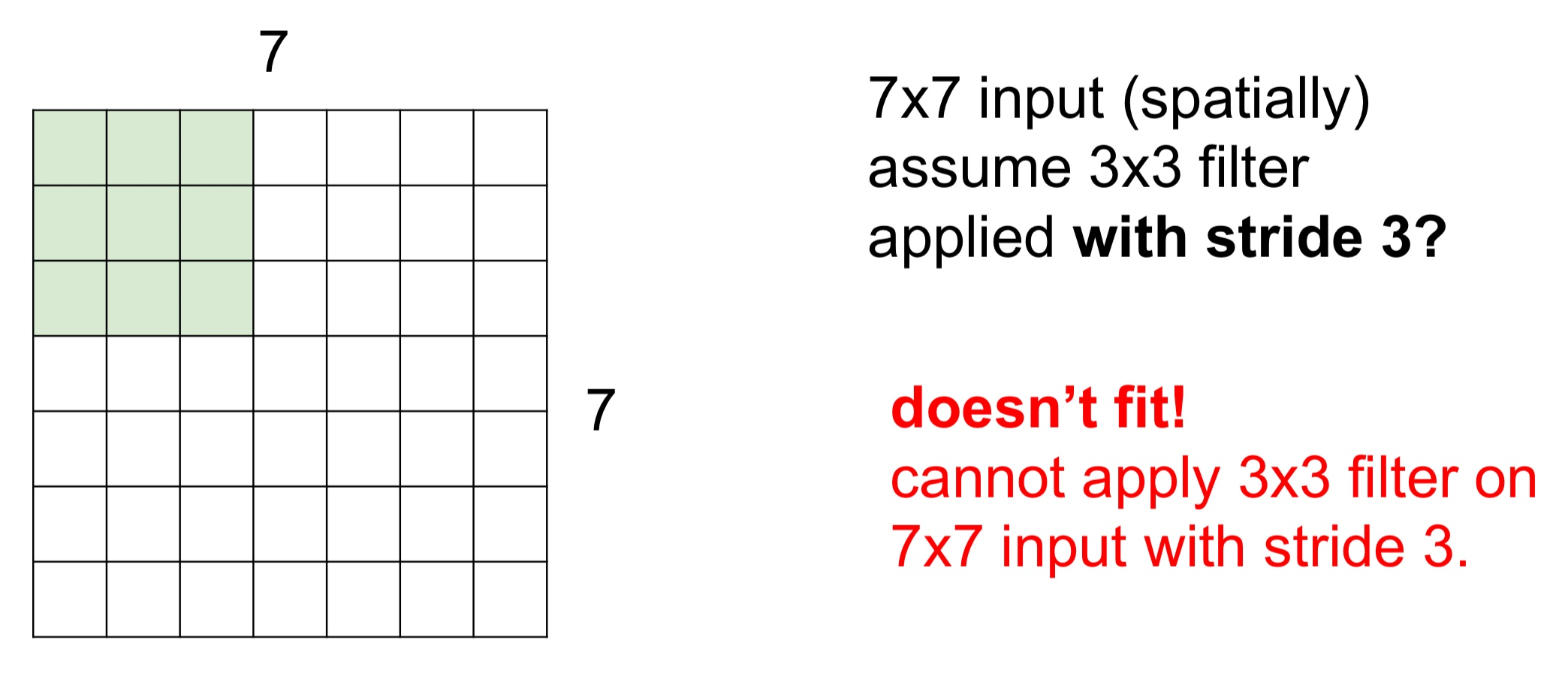
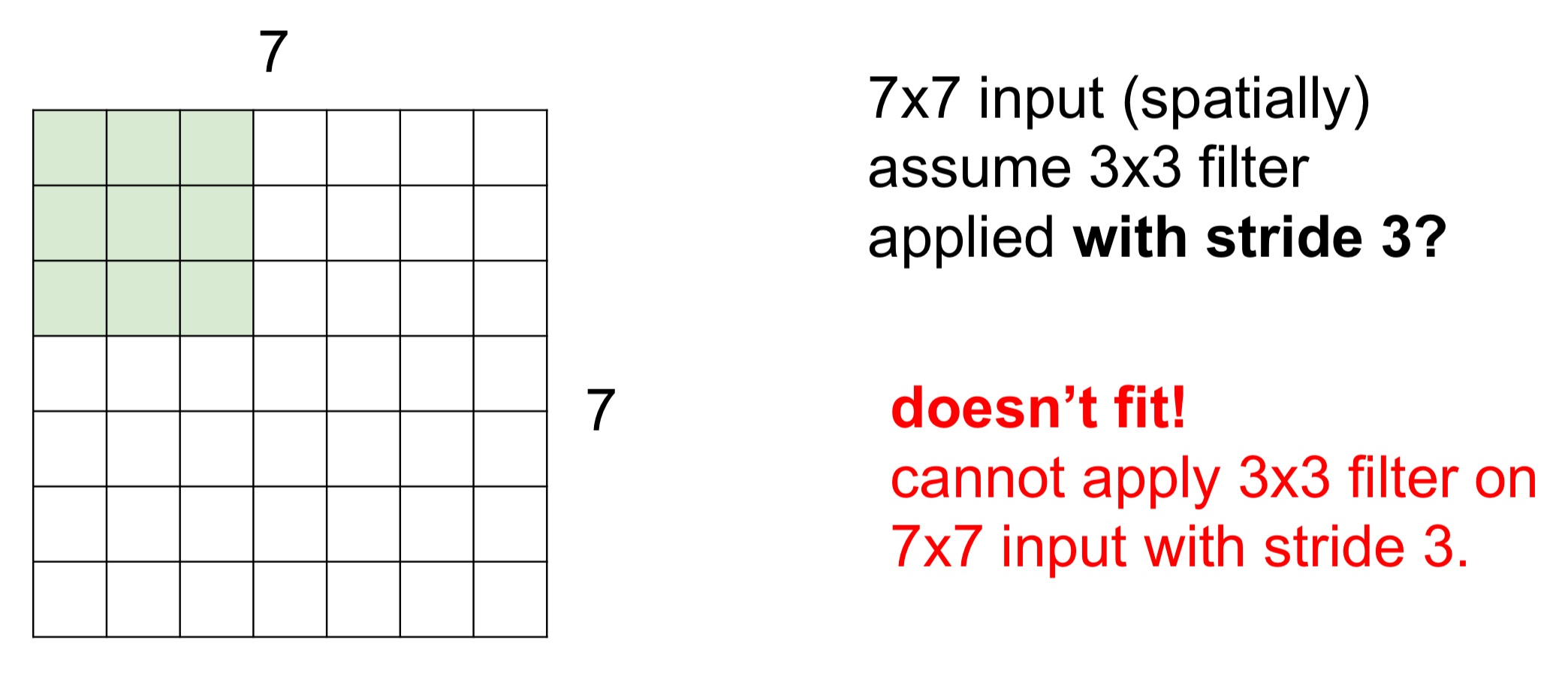
• Stide = 3인 경우 필터를 슬라이딩해도 필터가 모든 이미지를 커버할 수 없다
• 이미지가 딱 맞아 떨어지지 않으므로 학습이 잘 안되게 된다

• 이런 상황을 방지하고자 출력의 사이즈가 어떻게 될 것인지를 계산할 수 있는 식이 있다
• (N-F)/Stride + 1
  • N : 입력의 차원 수
  • F : 필터 사이즈
  • Stride : 필터 이동 간격
• 위 식을 이용하면 어떤 필터 크기를 사용해야 하는지 알 수 있다

Stride

• 필터가 입력 데이터에 대해 이동하는 간격을 의미한다
• 합성곱 연산을 수행할 때, 주어진 필터는 입력 데이터의 왼쪽 상단부터 시작하여 오른쪽 방향으로 이동하며 연산을 수행한다. 이 때, 한 번에 얼마나 이동하는지를 결정하는 것이 'Stride'이다
• Stride의 크기는 결과적으로 출력 특성 맵(Feature Map)의 크기를 결정하는 요소 중 하나이다
• Stride가 크면 출력 특성 맵의 크기는 작아지며, 반대로 Stride가 작으면 출력 특성 맵의 크기는 커진다

Zero-Padding

• 입력 데이터의 주변을 0으로 채우는 기법이다
• 주요 목적
  • 공간적 크기 보존
    • 합성곱 연산을 통과하면서 출력의 공간적 크기(가로 및 세로 차원)가 줄어드는 것을 방지한다
    • 즉, 입력과 동일한 공간적 크기를 가진 출력을 얻을 수 있다
  • 테두리 정보 보존
    • 입력 데이터의 중앙 부분이 아닌 테두리 부분에 있는 정보도 중요할 수 있다
    • Zero-Padding 없이 합성곱을 수행하면, 필터는 입력의 중앙 부분에 대해 더 많은 정보를 얻게 된다. 이는 테두리에 있는 정보가 손실되는 것을 의미한다
    • Zero-Padding을 사용하면 이 문제를 완화할 수 있다
• 제로 패딩의 크기는 보통 필터의 크기와 관련이 있다
  • 예를 들어, 3x3 크기의 필터를 사용하는 경우, 1픽셀의 제로 패딩을 사용하면 입력과 동일한 크기의 출력을 얻을 수 있다
• Zero-Padding을 사용하여 입력과 동일한 크기의 출력을 얻는 경우를 'Same'패딩이라고도 한다
• 반면, 제로 패딩을 전혀 사용하지 않는 경우를 'Valid' 패딩이라고 한다
  • 이 경우, 출력의 크기는 입력보다 작아진다

zero-padding을 사용하지 않는다면?

• 레이어가 여러겹 쌓이는 경우 zero-padding을 하지 않는다면 출력 사이즈는 아주 빠르게 줄어들게 된다
• 만일 엄청 깊은 네트워크가 있다고 생각해보면 Activation Map은 점점 줄어들어 엄청 작아지게 될 것이다
• 그렇게 되면 일부 정보를 잃게 되는 것이고 원본 이미지를 표현하기에 너무 작은 값을 사용하게 될 것이다
• 그렇게 줄어드는 이유는 매번 각 코너에 있는 값들을 계산하지 못하기 때문이다

stride와 filter를 쓸건지를 일반적으로 정하는 방법

• 보통 filter는 3x3, 5x5, 7x7을 쓴다
• 일반적으로 3x3 filter에는 stride를 1로 준다
• 그리고 5x5 filter에는 보통 stride를 2로 준다
• 7x7 일때는 stride를 3로 한다

1x1 Convolution

• CNN에서 사용되는 특별한 형태의 컨볼루션 연산
• 1x1 크기의 필터를 사용한다. 이는 입력 피쳐 맵의 각 픽셀에 대해 독립적으로 적용되며, 이를 통해 채널 간의 비선형성을 도입하고, 채널의 수를 조절하는 역할을 한다

주요 용도

• 차원 축소
  • 1x1 컨볼루션은 피쳐 맵의 채널 수를 줄여 계산 복잡성을 감소시키는 데 사용될 수 있다
  • 예를 들어, 64개의 입력 채널과 64개의 출력 채널이 있는 3x3 컨볼루션 대신에, 먼저 64개의 입력 채널을 32개의 채널로 줄이는 1x1 컨볼루션을 적용하고, 그 다음에 32개의 입력 채널과 64개의 출력 채널을 가진 3x3 컨볼루션을 적용함으로써, 계산량을 크게 줄일 수 있다
• 비선형성 도입
  • 1x1 컨볼루션 후에 비선형 활성화 함수(예: ReLU)를 적용함으로써, 모델에 추가적인 비선형성을 도입할 수 있다

Torch

• 딥러닝과 머신러닝 연구를 위한 오픈소스 라이브러리
• Torch는 다양한 최적화 알고리즘, 신경망 모듈, 전처리 기능 등을 제공하며, 특히 GPU를 활용한 계산에 강점이 있다
• 2015년 이후로는 Torch의 파생 버전인 'PyTorch'가 더 널리 사용되고 있다
• PyTorch는 Python 프로그래밍 언어로 작성되었으며, Torch의 핵심 기능을 유지하면서 동적 계산 그래프 기능 등을 추가하였다. 이는 모델을 좀 더 유연하게 구성하고 디버그하기 쉽게 만들어 주었다
• 다양한 레이어가 정의되어 있고 그 레이어의 forward/backward pass가 구현되어 있다

Pooling Layer

• Pooling Layer은 네트워크의 계산 부하를 줄이고, 공간적 변동성에 대한 허용 범위를 늘리는 역할을 한다
• 일반적으로 컨볼루션 레이어의 출력에 적용되며, 이는 이미지의 공간 차원(가로 및 세로)을 축소하면서 중요한 정보를 유지하도록 설계되었다
• 이 과정은 이미지 내의 작은 변화가 풀링 레이어를 통과하면서 덜 중요해짐으로써, 모델이 공간적 변동성에 대해 더 강인하게 만든다
• 풀링 레이어를 통해, 모델은 이미지의 전체적인 구조를 이해하는 데 더 집중할 수 있게 되며, 이는 과적합을 방지하고, 계산 효율성을 높이는 데 도움이 된다
• Pooling Layer은 Representation들을 더 작고 관리하게 쉽게 해주고, 다운 샘플링하여 공간적으로 줄여준다
• 중요한 점은 Depth에는 영향을 주지 않는다는 것이다
• 일반적으로 Max Pooling가 주로 쓰인다
• Pooling에도 필터 크기를 지정하여 얼마만큼의 영역을 한 번에 묶을지 설정할 수 있다
• pooling layer에서는 보통 padding을 하지 않는다
  • 풀링 레이어의 주요 목적은 입력 피쳐 맵의 공간적 크기를 줄이는 것이다. 즉, 너비와 높이 차원을 다운샘플링하여, 모델의 계산 부하를 줄이고 과적합을 방지하려는 것이다
  • 하지만 패딩을 사용하면 피쳐 맵의 공간적 크기가 보존되므로, 풀링 레이어의 이러한 목적에 부합하지 않게 된다
  • 또한, 패딩은 주로 컨볼루션 레이어에서 사용되는데, 이는 입력과 출력의 공간적 크기를 일치시키고, 이미지의 경계 부분에서도 유효한 피쳐를 추출하기 위함이다. 그러나 풀링 레이어에서는 일반적으로 이러한 요구사항이 없다

MAX Pooling

• CNN에서 널리 사용되는 폴링 기법이다

• 입력 피쳐 맵의 서브 영역(sub-region)에 대해 최대값을 선택하여, 그 영역을 대표하는 값으로 사용한다

• Conv Layer가 했던 것 처럼 슬라이딩하면서 연산을 수행한다

• 대신 내적을 하는 것이 아니라, 필터 안에 가장 큰 값 중에 하나를 고르는 것이다

주요 특징

• 차원 축소
  • Max 풀링은 피쳐 맵의 공간적 크기(가로 및 세로 차원)를 줄여, 모델의 파라미터 수와 계산량을 감소시키며 과적합을 방지하는 데 도움이 된다
• 변동성에 대한 강인성
  • Max 풀링은 작은 위치 변화에 대해 강인하다
  • 즉, 이미지 내의 객체가 약간 이동하더라도, Max 풀링 후의 출력은 크게 바뀌지 않는다
  • 이는 모델이 특정 객체의 정확한 위치보다는 그 객체의 존재 유무를 더 중요하게 여기도록 돕는다
• 핵심 피쳐 강조
  • Max 풀링은 각 서브 영역에서 가장 두드러진 피쳐를 선택한다
  • 이는 대표적인 피쳐를 강조하고, 덜 중요한 정보를 걸러내는 역할을 한다

Average Pooling

• 피쳐 맵의 차원(일반적으로 너비와 높이)을 줄이는 데 사용된다
• Avg 폴링은 주어진 피쳐 맵의 영역(일반적으로 정사각형)의 픽셀 값을 평균 내어 그 영역을 대표하는 하나의 값으로 만드는 연산이다
• 이를 통해 피쳐 맵의 크기가 줄어들며, 이는 계산량을 줄이고, 모델의 과적합 가능성을 감소시키는 데 도움이 된다
• 평균 풀링은 영역 내의 모든 픽셀 값을 고려하므로, 더 부드러운 피쳐 맵을 생성하지만, 최대 풀링처럼 가장 두드러진 피쳐만을 보존하는 것은 아니다

요약

• 기본적으로는 Conv와 Pool를 쌓아 올리다가 마지막에 FC Layer로 끝나게 된다. 그리고 네트워크의 필터는 점점 더 작아지고, 아키텍쳐는 점점 깊어지는 경향을 띈다
• 최근에는 Pooling 이나 FC Layer를 점점 더 없애는 추세이기도 하다. 그냥 Conv Layer만 깊게 쌓는 것이다
• 전형적인 CNN 아키텍쳐는 Conv와 ReLU를 몇 번(n번) 반복한다. 그리고 그 중간에 pooling도 몇 번 들어간다. 그리고 FC Layer가 이어진다. 한 번에서 두 번 그 이상일수도 있다
• Class score를 구하기 위해서는 보통 softmax를 사용한다
• 일반적으로 n은 5 정도가 될 수 있다
• 그렇게 되면 엄청 깊은 Conv, ReLU, Pool 시퀀스를 구성하게 될 것이고, 그다음 한 두번의 FC Layer가 이어진다

출처 및 참조

https://youtu.be/bNb2fEVKeEo?si=w74487u4StAOmGUG