Activation Functions

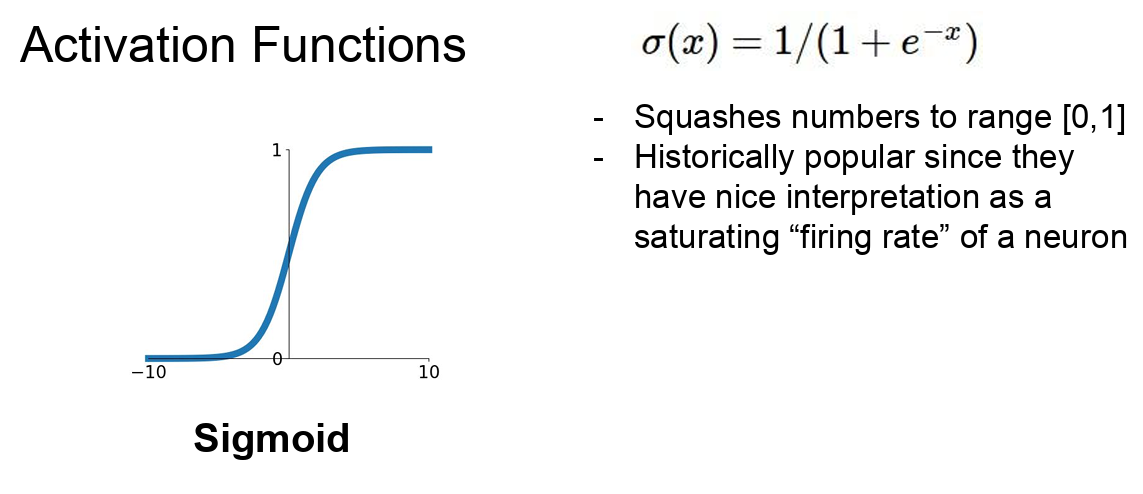
Sigmoid

특징

• 실수 입력을 받아서 그 입력을 [0, 1] 사이의 값을 출력하는 S-형 커브를 그리는 특성이 있다
• 입력의 값이 크면 Sigmoid의 출력은 1에 가깝고 값이 작으면 0에 가깝다
• 0 근처 구간(rigime)은 선형함수처럼 보인다
• 출력 범위가 [0, 1]이기 때문에 확률을 나타내는 데 사용될 수 있으므로, 이진 분류 문제에서 출력 레이어의 활성화 함수로 자주 사용된다

• Sigmoid 함수는 비선형 함수이다. 이는 선형 변환 후에 적용되어 신경망에 복잡성을 부여하며, 복잡한 패턴을 학습하는 데 필요하다
• Sigmoid는 역사적으로 아주 유명했다. 왜냐하면 Sigmoid가 일종의, 뉴런의 firing rate(뉴런의 활성화률)를 saturation(포화)시키는 것으로 해석할 수 있기 때문이다
• 어떤 값이 0에서 1 사이의 값을 가지면 이를 fireing rate라고 생각할 수 있다

문제점

• Saturation(포화) 되는게 gradient를 없앤다
  • 시그모이드 함수는 그 형태가 S 모양이며, 입력값이 매우 크거나 작을 때 함수의 출력값이 각각 1 또는 0에 가까워진다. 이 영역에서의 시그모이드 함수의 기울기는 매우 작아져서 0에 가까워진다
  • 기울기가 0에 가까워지는 현상을 Saturated라고 하고 이것은 Vanising Gradient 문제를 일으킨다
• sigmoid의 출력이 zero centered 하지 않다
  • sigmoid의 출력 범위는 [0, 1]이기 때문에 출력은 항상 양수이다
  • 출력이 항상 양수이면 기울기는 항상 같은 부호를 가진다. 이는 가중치의 업데이트가 일정한 방향으로 치우치게 되어, 최적화 과정에서 비효율적인 움직임을 보일 수 있다
• exp()로 인해 계산비용이 크다
  • 이건 그닥 큰 문제는 아니다
  • 큰 그림으로 봤을 때 다른 연산들, 가령 내적의 더 계산 비용이 더 비싸다

Tanh(Hyperbolic Tangent)

특징

• sigmoid와 유사하지만 출력 범위가 [-1, 1] 이다
• sigmoid와 가장 큰 차이점은 zero-centered 라는 것이다. 이는 출력이 0을 중심으로 하기 때문에, 시그모이드 함수에 비해 기울기 소실 문제를 덜 경험하며, 학습이 더 잘 일어나는 경향이 있다
• Tanh 함수는 비선형 함수이다. 이는 선형 변환 후에 적용되어 신경망에 복잡성을 부여하며, 복잡한 패턴을 학습하는 데 필요하다

문제점

• 여전히 saturation때문에 Gradient가 죽는다(여전히 gradient가 평평해 지는 구간이 있다)
  • sigmoid와 마찬가지로 입력의 절대값이 큰 경우에 기울기가 매우 작아지는 문제가 있다
  • 이는 역전파 과정에서 그래디언트가 신경망의 초기 레이어에 제대로 전달되지 않는 그래디언트 소실(Vanishing Gradient) 문제를 일으킬 수 있다

ReLU

특징

• ReLU의 함수는 f(x) = max(0, x) 이다
  • 입력이 0 이상일 경우 그대로의 값을 반환하고, 0 미만일 경우 0을 반환하는 간단한 함수이다
• element-wise 연산을 수행하며 입력이 음수면 값이 0이 된다. 그리고 양수면 입력 값 그대로를 출력한다
• ReLU는 양의 값에서는 saturetion 되지 않는다
  • 적어도 입력스페이스의 절반은 saturation 되지 않는다
  • 양수 영역에서 기울기가 항상 1이므로, 신경망이 깊어져도 역전파 시 기울기가 소실되는 문제를 완화할 수 있다
• 그리고 계산 효율이 아주 뛰어나다
  • ReLU는 단순히 max 연산이므로 계산이 매우 빠르다
  • 실제로 sigmoid나 tanh보다 수렴속도가 6배 정도로 훨씬 빠르다
• ReLU 함수는 비선형 함수이다. 이는 선형 변환 후에 적용되어 신경망에 복잡성을 부여하며, 복잡한 패턴을 학습하는 데 필요하다
• 생물학적 타당성도 ReLU가 sigmoid 보다 크다

문제점

• zero-centered가 아니다
• ReLU에서 양의 수에서는 saturation 되지 않지만 음의 경우에서는 그렇지 않다
  • 기본적으로 ReLU는 gradient의 절반을 죽여버리는 셈이다
  • dead ReLU 현상을 겪을 수 있다

dead ReLU

설명

• 입력이 0 미만인 영역에서 ReLU의 기울기는 항상 0이므로, 일부 뉴런이 활성화되지 않고 '죽게' 될 수 있다
• 이렇게 되면 그 뉴런은 그래디언트를 전파받지 못하게 되어, 더 이상 학습이 진행되지 않게 된다
• ReLU가 data cloud에서 떨어져 있는 경우에 dead ReLU가 발생한다
• dead ReLU에서는 activate가 일어나지 않고 update되지 않는다

발생하는 이유

• 초기화를 잘 못한 경우
  • 가중치 평면이 data cloud에서 멀리 떨어져 있는 경우
  • 이런 경우 어떤 데이터 입력에서도 activate 되는 경우가 존재하지 않을 것이고 backporp이 일어나지 않을 것이다
  • 이런 경우 update되지도 activate되지도 않을 것이다
• Leraning rate가 지나치게 높은 경우
  • 처음에 "적절한 ReLU"로 시작할 수 있다고 해도 만약 update를 지나치게 크게 해 버려 가중치가 날뛴다면 ReLU가 데이터의 manifold를 벗어나게 된다
  • 이런 일들은 학습과정에서 충분히 일어날 수 있다. 그래서 처음에는 학습이 잘 되다가 갑자기 죽어버리는 경우가 생기는 것이다

Leaky ReLU

• ReLU와 유사하지만 입력 값이 음수일 경우에도 아주 작은 기울기를 가지는 것으로 negarive regime에서 더 이상 0이 아니다
• negative에도 기울기를 살짝 주게 되면 앞서 설명했던 문제를 상당 부분 해결하게 된다
• Leaky ReLU의 경우에는 negative space에서도 saturation 되지 않는다
• ReLU와 마찬가지로 계산이 효율적이다. 그리고 sigmoid 나 tanh보다 수렴을 빨리 할 수 있다. 그리고 dead ReLU 현상도 더 이상 없다
• f(x) = max(0.01x, x)에서 0.01이라는 값은 하이퍼파라미터로, 이 값이 Leaky ReLU의 '누출'을 결정한다

PReLU(parametric rectifier)

• PReLU는 negative space에 기울기가 있다는 점에서 Leaky ReLU와 유사하다
• Leaky ReLU에서는 음수 영역에서의 기울기가 고정된 작은 값(예: 0.01)이었다면, PReLU에서는 이 값이 학습 과정에서 최적화되는 파라미터로 바뀌었다
• 이를 통해, 모델이 필요에 따라 음수 영역에서의 기울기를 자동으로 조절할 수 있게 되었다
• 여기서 α는 학습 가능한 파라미터로, 일반적으로 a는 0에 가까운 작은 값으로 초기화되며, 학습 과정에서 backprop으로 업데이트된다
• PReLU는 '죽은 ReLU' 문제를 더욱 효과적으로 해결하며, 일반적으로 CNN과 같은 깊은 신경망에서 좋은 성능을 보인다
• 활성함수가 조금 더 유연해 질 수 있다

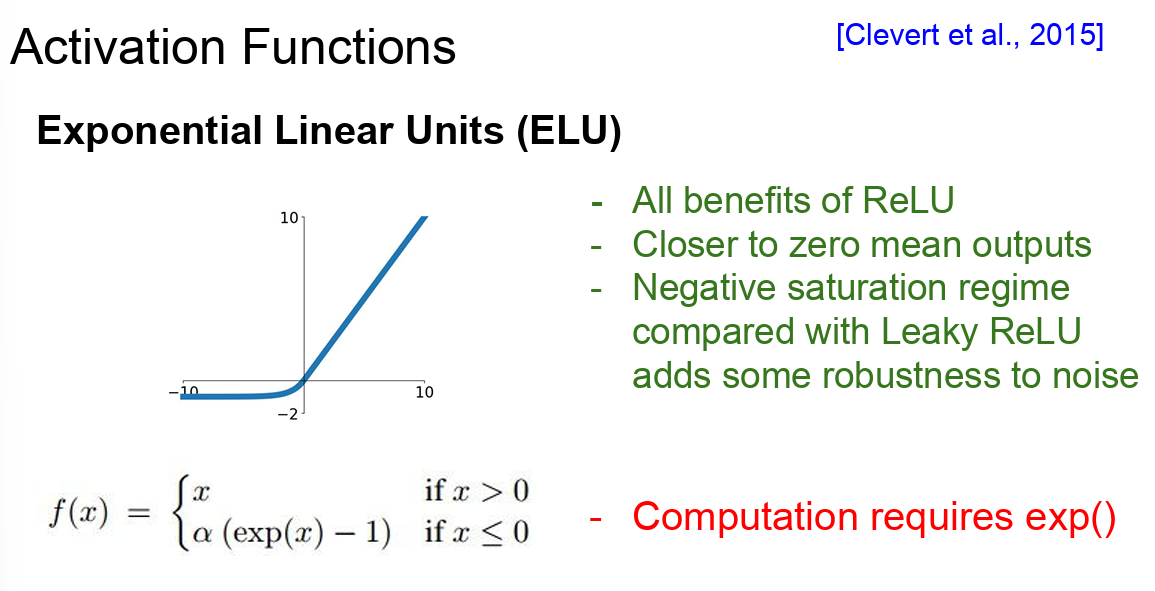
ELU

• ReLU(Rectified Linear Unit)의 변형된 형태로, 음수 입력에 대해 새로운 동작을 정의함으로써 ReLU의 몇 가지 단점을 극복했다
• ELU의 수식에서 α는 하이퍼파라미터로, 보통 1.0으로 설정된다
• ELU는 ReLU의 이점을 그대로 계승했다
• ELU는 zero-mean에 가까운 출력값을 보인다
  • zero-mean에 가까운 출력은 앞서 leaky ReLU, PReLU가 가진 이점이다
  • 이는 학습 과정의 안정성을 높여준다
• 음수 입력에 대해 0이 아닌 값을 출력하므로, '죽은 ReLU' 문제를 완화한다
• 입력의 변화에 대해 부드럽게 변하는 특성으로 인해, 그래디언트의 변화가 더 안정적이다
• 하지만 Leaky ReLU와 비교해보면 ELU는 negative에서 "기울기" 를 가지는 것 대신에 또 다시 "saturation"이 된다
• ELU가 주장하는건 이런 saturation이 좀 더 잡음(noise)에 강인할 수 있다는 것이다
• ELU는 Leaky ReLU처럼 zero-mean의 출력을 내지만 Saturation의 관점에서 ReLU의 특성도 가지고 있다

Maxout Neuron

• 입력값의 선형 변환 결과 중에서 최대값을 출력하는 방식으로 동작한다
• 입력을 받아드리는 특정한 기본형식을 미리 정의하지 않는다. 대신에 w1에 x를 내적한 값 + b1과 w2에 x를 내적한 값 + b2의 최댓값을 사용한다
  • x : 입력 벡터
  • w1, w2 : 가중치 벡터
  • b1, b2 : 편향값
• Maxout은 이 두 함수 중 최댓값을 취한다
• Maxout는 ReLU와 leaky ReLU의 좀 더 일반화된 형태이다. 왜냐하면 Maxout은 이 두 개의 선형함수를 취하기 때문이다
• Maxout 또한 선형이기때문에 saturation 되지 않으며 gradient가 죽지 않는다
• 기존의 활성화 함수(예: ReLU, sigmoid, tanh 등)와 달리, Maxout 함수는 입력값에 대해 비선형이 아닌 '조각별 선형(piecewise linear)' 동작을 한다. 이는 Maxout 함수가 다양한 함수를 근사할 수 있게 한다
• ReLU와 마찬가지로, Maxout 함수는 'dead ReLU' 문제를 해결한다
• 문제점
  • 뉴런당 파라미터의 수가 두 배가 된다는 것이다
  • 가중치 벡터 W1과 W2를 지니고 있어야 한다

Data Preprocessing(데이터 전처리)

• 머신러닝이나 데이터 분석을 수행하기 전에 데이터를 적절한 형태로 변환하는 과정을 말한다

• 원본 데이터는 종종 결측값이 있거나, 일관성이 없거나, 노이즈가 섞여 있는 등 여러 가지 문제를 가지고 있을 수 있다. 이러한 문제를 해결하고, 머신러닝 알고리즘이 더 효과적으로 학습할 수 있도록 데이터를 정제하는 것이 데이터 전처리의 목표이다

• 일반적으로 입력 데이터는 전처리를 해준다

• 가장 대표적인 전처리 과정은 "zero-mean"으로 만들고 "normalize" 하는 것이다

  • normalization(정규화)은 보통 표준편차로 한다
  • normalization을 해주는 이유는 모든 차원이 동일한 범위안 있게 해줘서 전부 동등한 기여(contribute)를 하게 하기 때문이다

• 실제로는 이미지의 경우 전처리로 zero-centering 정도만 하고, normalization 하지는 않는다. 왜냐하면 이미지는 이미 각 차원 간에 스케일이 어느정도 맞춰져 있기 때문이다. 따라서 스케일이 다양한 여러 ML 문제와는 달리 이미지에서는 normalization을 엄청 잘 해줄 필요는 없다

• 일반적으로는 이미지를 다룰 때는 굳이 입력을 더 낮은 차원으로 projection 시키지 않는다

  • 일부 머신러닝 알고리즘에서는 계산 효율성이나 과적합 등의 이유로 데이터의 차원을 축소하는 것이 필요할 수 있다
  • 그러나 이미지 데이터를 다루는 딥러닝, 특히 CNN에서는 이미지의 공간적 구조를 이용하여 특징을 추출하기 때문에, 입력 이미지의 차원을 그대로 유지하는 것이 일반적이다

• CNN에서는 원본 이미지 자체의 spatial 정보를 이용해서 이미지의 spatial structure를 얻을 수 있도록 한다

• 요약하자면 이미지를 다룰때는 기본적으로 zero-mean 으로 전처리를 해준다는 것이다

• 평균 값은 전체 Training data에서 계산한다

• 보통 입력 이미지의 사이즈를 서로 맞춰주는데 가령 32x32x3이고 네트워크에 들어가기 전에 평균값을 빼주게 된다

• 그리고 Test time의 이미지에도 Training time에 계산한 평균 값으로 빼주게 된다

출처 및 참조

https://youtu.be/wEoyxE0GP2M?si=uDXI1LG_zrb5r6mH